¡Hola de nuevo, aspirante! Continuamos resolviendo la el examen simulacro de temas de la guía del EXANI II en el módulo de Probabilidad y Estadística. En esta segunda parte, vamos a realizar desde el reactivo 11 hasta el 20.
Recuerda primero intentar resolverlos por tu cuenta, antes de consultar el procedimiento correcto para responderlo.
Curso Exani II 2024
Reactivo 11
La mediana, es un parámetro estadístico que cuantifica la ________ de un conjunto de datos.
- Tendencia media
- Posición
- Dispersión respecto a la media
Solución:
La mediana, junto a la media y la moda, son medidas de tendencia central en la estadística descriptiva. Específicamente, la mediana indica el valor central de un conjunto de datos. Aquel que divide al conjunto en dos subconjuntos con la misma cantidad de elementos.
El inciso que completa de forma correcta al enunciado es el a).
La mediana, es un parámetro estadístico que cuantifica la tendencia media de un conjunto de datos.
Reactivo 12
Durante una práctica de béisbol, el entrenador decide medir la desviación de algunos de los tiros a home de su pitcher. Las mediciones fueron realizadas desde el guante del catcher hasta el punto en que recibe la bola del pitcher.
La siguiente tabla contiene las mediciones separadas en 3 intervalos.
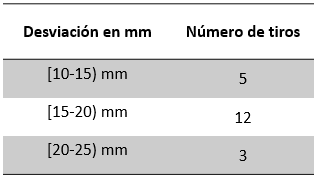
Calcula la desviación típica de los tiros realizados por el pitcher.
- 4.12 mm
- 3.12 mm
- 5.12 mm
Solución:
Debido a que los datos se encuentran agrupados, debemos calcular la desviación típica aplicando para datos agrupados por intervalos. Para simplificar la visualización de la solución, vamos a expresar los procedimientos en tablas.
Desviación típica.
s=\sqrt{\frac{\sum {f}_{i}\cdot {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{N}}
Debido a que no hay más población, sino la dada por la tabla del enunciado, trabajamos con la fórmula de la desviación típica para una población. Iniciamos calculando la marca de clase {x}_{i} .
Fórmula de la marca de clase.
{x}_{i}=\frac{{M}_{i}+{L}_{i}}{2}
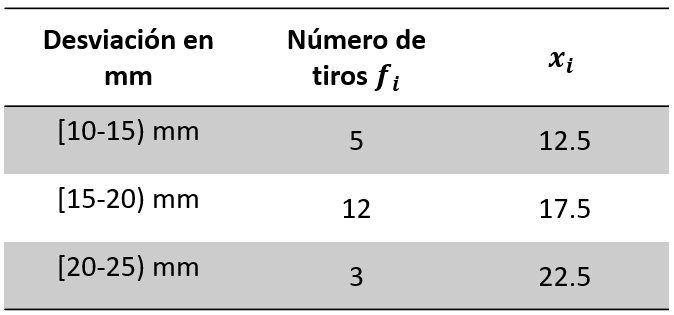
Calculamos la media del conjunto de datos.
\stackrel{-}{x}=\frac{12.5\cdot 5+17.5\cdot 12+22.5\cdot 3}{5+12+3}=17 \mathrm{m}\mathrm{m}
Creamos una nueva columna en la tabla para calcular {f}_{i}\cdot {\left({x}_{i}-\stackrel{-}{x}\right)}^{2} .
Finalmente, sustituimos este resultado en la ecuación de desviación.
s=\sqrt{\frac{\sum {f}_{i}\cdot {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{N}}=s=\sqrt{\frac{195}{5+12+3}}=3.12 \mathrm{m}\mathrm{m}
La desviación típica del pitcher es de 3.12 milímetros respecto del guante del receptor.
Comparando con los incisos, la respuesta correcta es el b).
Reactivo 13
Teniendo en cuenta los datos de las ventas de la tienda de celulares: 7, 8, 9, 6, 7, 8, 8, 5, 7, 13, 7, 6, 6 y 4; calcula la varianza en el número de unidades vendidas.
- 14
- 7.21
- 4.16
Solución:
Examinando los datos, vemos que se trata de un conjunto desagrupado. Procedemos a ordenarlos de menor a mayor.
4, 5, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 9, 13
La varianza se calcula como:
{s}^{2}=\frac{\sum {{f}_{i}\cdot \left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{N}
Calculamos la media.
\stackrel{-}{x}=\frac{4+5+6+6+6+7+7+7+7+8+8+8+9+13}{14}=7.21
Para calcular {f}_{i}\cdot {\left({x}_{i}-\stackrel{-}{x}\right)}^{2} , empleamos una sencilla tabla.
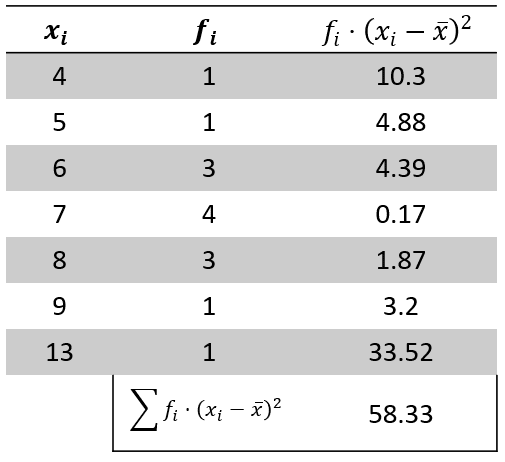
Finalmente, sustituimos en la expresión de la varianza.
{s}^{2}=\frac{58.33}{14}=4.16
La varianza del conjunto de datos es igual a 4.16.
La respuesta correcta es el inciso c).
Reactivo 14
Determina el percentil 50 del siguiente conjunto de datos.
41 44 45 45 41 42 40 39 38 37 37
- 42.5
- 41
- 45
Solución:
El percentil 50 corresponde con la mediana y con el cuartil 2. Estos tres parámetros determinan al elemento que divide al conjunto de datos en dos subconjuntos con la misma cantidad de elementos. Ordenamos el conjunto de datos.
37, 37, 38, 39, 40, 41, 41, 42, 44, 45, 45
Debido a que el conjunto de datos es impar (hay 11 elementos), el elemento que lo divide en partes iguales es el que se encuentra en la posición 6.
El percentil 50 es el número 41.
La respuesta correcta es el inciso b).
Reactivo 15
En base a la siguiente tabla de datos agrupados, calcule su media.
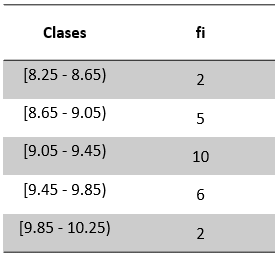
- 9.26
- 8.82
- 3.45
Solución:
Emplearemos la misma tabla para ir plasmando los resultados. Debido a que los datos se encuentran agrupados, debemos calcular la marca de clase {x}_{i} para cada intervalo.
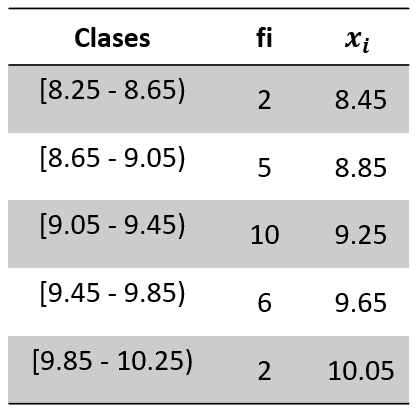
Finalmente, calculamos la media como:
\stackrel{-}{x}=\frac{\sum {f}_{i}\cdot {x}_{i}}{N}=\frac{\left(8.45\right)\left(2\right)+\left(8.85\right)\left(5\right)+\left(9.25\right)\left(10\right)+\left(9.65\right)\left(6\right)+\left(10.05\right)\left(2\right)}{2+5+10+6+2}
\stackrel{-}{x}=\frac{231.65}{25}=9.26
La respuesta correcta es el inciso a).
Reactivo 16
Un viajero compra un candado de seguridad para su maleta. El viajero debe establecer una clave de 4 dígitos con los números del 0 al 9. ¿Cuántas posibles claves puede establecer el viajero si no se le permite repetir ningún número?
- 2550
- 1000
- 5040
Solución:
Siempre que tratamos con claves o códigos en problemas de conteo, sin dudarlo se trata de una permutación/variación debido a que importa el orden. Ahora, no intervienen todos los elementos, porque los números del 0 al 9 son 10 y las claves son de 4 dígitos, se trata de una variación.
Por otro lado, no se permite repetir elementos. Concluimos que es una variación ordinaria.
{V}_{\mathrm{10,4}}=\frac{10!}{\left(10-4\right)!}=\frac{10!}{6!}=\frac{10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}=10\cdot 9\cdot 8\cdot 7=5040
Se pueden establecer 5040 claves distintas.
La respuesta correcta es el inciso c).
Reactivo 17
Se tiran dos dados regulares de 6 caras y un evento A que consiste en obtener como resultado de sumar el resultado en ambos dados un número menor o igual que 4. ¿Cuál es el espacio muestral del evento A?
- \left\{\left(1, 1\right),\left(1, 2\right),\left(2, 1\right),\left(2, 2\right),\left(3, 1\right),\left(1, 3\right)\right\}
- \left\{\left(1, 1\right),\left(2, 2\right), \left(3, 1\right),\left(1, 3\right)\right\}
- \left\{\left(1, 2\right),\left(2, 1\right), \left(3, 1\right),\left(1, 3\right)\right\}
Solución:
En el lanzamiento de dos dados regulares de 6 caras, tenemos como posibles resultados:
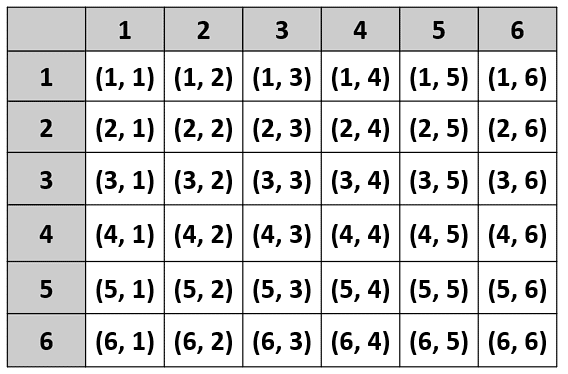
Ahora señalamos aquellos pares que sumen igual o menor que 4.
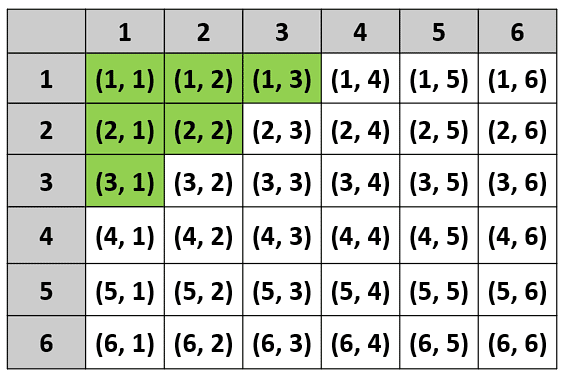
Comparando con los incisos de las casillas señaladas, concluimos que la respuesta correcta es el a).
Reactivo 18
¿Cuál es la magnitud del espacio muestral al lanzar 3 dados regulares de 6 caras?
- 18
- 36
- 216
Solución:
El espacio muestral es el total de los posibles resultados. Si son 3 dados y cada dado tiene 6 posibles resultados, aplicamos la fórmula de una variación con repetición.
{\mathrm{V}\mathrm{R}}_{6,\mathrm{ }3}={6}^{3}=216
La respuesta correcta es el inciso c).
Reactivo 19
Un sistema digital recibe a su entrada 8 dígitos binarios, donde cada uno puede ser 0 o 1. ¿Cuántos valores pueden ser representados a la entrada del sistema digital?
- 16
- 256
- 255
Solución:
En este caso, tenemos 8 espacios donde cada uno puede tomar el valor de 1 o 0. Debido a que importa el orden, no intervienen todos los elementos (porque hay más espacios que elementos) y se permite la repetición, emplearemos la fórmula de variaciones con repetición.
El total de elementos es igual a m=2 (0 o 1) y los espacios son n=8 .
{\mathrm{V}\mathrm{R}}_{\mathrm{2,8}}={m}^{n}={2}^{8}=256
Se pueden obtener 256 cantidades diferentes.
La respuesta correcta es el inciso b).
Examen simulacro: Probabilidad y estadística
Reactivo 20
Jesús ha cambiado la clave de su wifi, pero solo recuerda los 3 primeros dígitos, le faltan los últimos 4. Él está seguro de que solo se trata de números comprendidos entre el 0 y el 5, y que ninguno está repetido.
¿Cuál es la probabilidad de que Jesús encuentre la clave correcta probando cada posibilidad?
- \frac{1}{360}
- \frac{5}{360}
- \frac{10}{360}
Solución:
En este caso, debemos calcular el total de claves que pueden formarse con los 4 dígitos disponibles contando con los números del 0 al 5. Luego de esto, la probabilidad la calculamos como la única clave correcta sobre el total de posibilidades.
Los números se agrupan de 4 en 4, importa el orden porque es una clave, contamos con 6 elementos y no se permiten repeticiones: empleamos la fórmula de variaciones ordinarias.
{\mathrm{V}}_{\mathrm{5,4}}=\frac{6!}{\left(6-4\right)!}=\frac{6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{2\cdot 1}=360
Finalmente:
\mathrm{P}=\frac{1}{360}\approx 0.0028
La respuesta correcta es el inciso a).
Hola, mi nombre es Fernando Toxqui y llevo más de una década como docente especializado en matemáticas, con un enfoque particular en la preparación para exámenes de admisión.
