Continuamos resolviendo la el examen simulador de los temas oficiales de la guía del EXANI II en el módulo de Probabilidad y Estadística. En esta cuarta parte, vamos a realizar desde el reactivo 31 hasta el 40.

Desarróllalos por tu cuenta antes de mirar la solución. Utiliza este material como medio de consulta y para salir de dudas.
Reactivo 31
¿Cuál es la moda del conjunto de datos mostrado a continuación?
1, 2, 2, 3, 2, 5, 6, 7, 8, 8, 10, 11, 22, 8, 8
- El número 2
- El número 8
- El número 1
Solución:
Iniciamos ordenando, de menor a mayor, al conjunto de datos.
1, 2, 2, 2, 3, 5, 6, 7, 8, 8, 8, 8, 10, 11, 22
La moda es el valor que más se repite en el conjunto de datos. Examinando los datos del enunciado, concluimos que la moda es el número 8, ya que se repite 4 veces. La respuesta correcta es el inciso b).
Reactivo 32
La mediana de un conjunto de datos, es igual al…
- Percentil 45
- Cuartil 3
- Percentil 50
Solución:
La mediana es un parámetro estadístico de tendencia central que representa al elemento que divide al conjunto de datos en dos subconjuntos con la misma cantidad de elementos. Comparada con los percentiles, la mediana concuerda con el percentil 50.
La respuesta correcta es el inciso c).
Añadido
Reactivo 33
Un experimento aleatorio consiste en lanzar al aire tres veces una moneda. Calcule la probabilidad de obtener Águila en el primer lanzamiento.
- 0.432
- 0.5
- 0.245
Solución:
Debido a que es el primer lanzamiento, la probabilidad de obtener Águila se calcula como:
P\left({A}_{1}\right)=\frac{1}{2}=0.5
La respuesta correcta es el inciso b).
Reactivo 34
La estación de policía en determinada región del país se encuentra realizando un estudio estadístico de la situación de las multas en cierto punto de control. La siguiente tabla recoge las multas emitidas durante una semana.
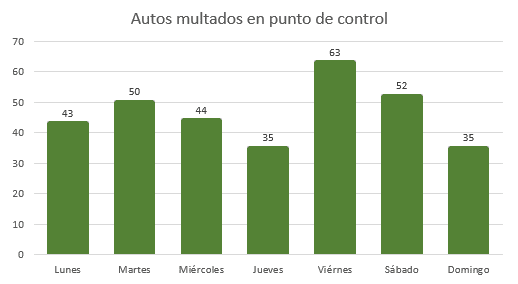
¿Cuál o cuáles de los días de la semana se encuentran por encima de la media?
- Martes, viernes y sábado
- Martes y viernes
- Viernes
Solución:
Iniciamos calculando la media del conjunto de datos.
\stackrel{-}{x}=\frac{43+50+44+35+63+52+35}{7}=46
Debemos identificar los días de la semana con multas por encima de 46. Estos son:
Martes, viernes y sábado.
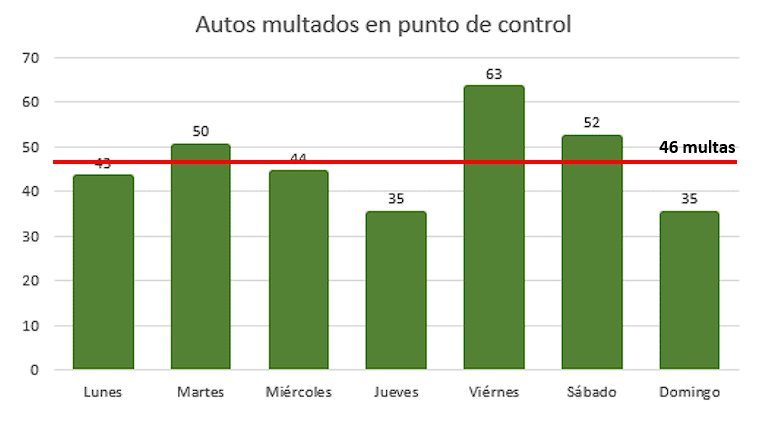
La respuesta correcta es el inciso a).
Reactivo 35
El criterio de Norcliffe para encontrar el número de clases para un conjunto de datos desagrupados establece que…
- Debe ser igual a la mitad de la cantidad de datos
- Debe ser igual a la raíz cúbica de la cantidad de datos
- Debe ser igual a la raíz cuadrada de la cantidad de datos
Solución:
Cuando el número de valores distintos que toma la variable estadística es considerable, conviene agrupar a la población en clases o intervalos. Existen diferentes criterios para determinar el número de clases que debe tener el conjunto.
El criterio de Norcliffe establece que el número de clases debe ser igual a la raíz cuadrada del número de datos. Teniendo esto en cuenta y examinando los incisos, concluimos que la respuesta correcta es c).
Reactivo 36
En un instituto se sabe que el 55% de la población estudiantil es femenino. Un 25% de las estudiantes posee promedio académico mayor a 8.5, mientras que solo el 20% de los varones tiene un promedio similar.
¿Cuál es la probabilidad de escoger un estudiante al azar y que tenga promedio mayor a 8,5?
- 35
- 23
- 45
Solución:
Debido a que tenemos un 55% de chicas con un 25% de promedios por encima de 8.5 y un 45% de chicos con promedio superior a 8.5.
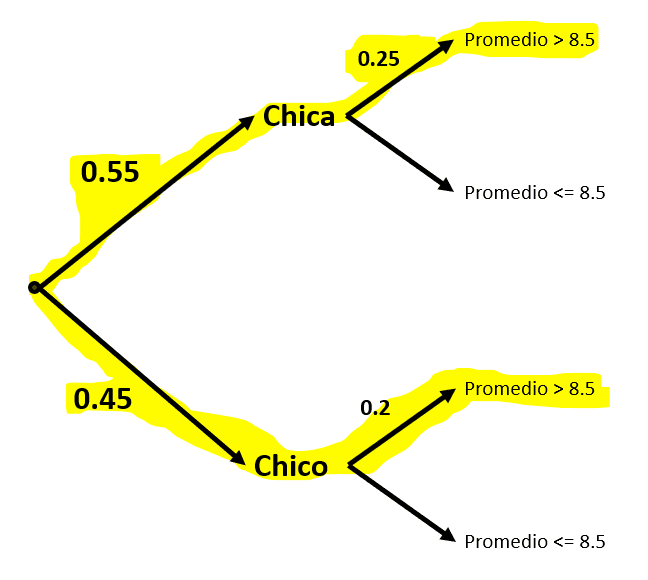
La probabilidad de escoger un estudiante al azar y que tenga promedio por encima de 8.5 es igual a la suma de la probabilidad de que sea chica con promedio mayor a 8.5 más, la probabilidad de que sea chico con promedio mayor a 8.5.
Probabilidad de que sea chico y tenga promedio mayor a 8.5.
P\left(M\right)=\left(0.45\right)\left(0.2\right)=0.09
Probabilidad de que sea chica y tenga promedio mayor a 8.5.
P\left(F\right)=\left(0.55\right)\left(0.25\right)=0.14
Sumamos ambas probabilidades.
P\left(>8.5\right)=0.09+0.14=0.23
La respuesta correcta es el inciso b).
Reactivo 37
Un estudio ha revelado que el 15% de las familias en una ciudad posee más de un automóvil propio, el 30% uno y el resto debe emplear el transporte público.
¿Qué es más común en esta ciudad, tener automóvil o utilizar el transporte público?
- Tener más de uno
- Tener al menos uno
- Utilizar transporte público
Solución:
Tenemos que apenas el 15% de la población posee más de un automóvil, el 30% tiene al menos uno, pero el restante 55% necesita utilizar transporte público. Por tanto, es más común que se utilice el transporte público.
La respuesta correcta es el inciso c).
Reactivo 38
Cuando tenemos un conjunto de datos agrupados la moda le corresponde a la _____ con mayor _______.
- Frecuencia, desviación
- Clase, desviación
- Clase, frecuencia
Solución:
Cuando tenemos datos agrupados, la clase modal es aquella con mayor frecuencia absoluta o relativa. Luego de identificar la clase modal, se emplea la fórmula M={L}_{i}+\left(\frac{{D}_{1}}{{D}_{1}+{D}_{2}}\right){A}_{i} para calcular el valor de la moda.
Cuando tenemos un conjunto de datos agrupados, la moda le corresponde a la clase con mayor frecuencia.
Concluimos que la respuesta correcta es el inciso c).
Reactivo 39
A partir de los datos agrupados en la siguiente tabla, encuentre el percentil 40.

- 57.25
- 58
- 74
Solución:
Para datos agrupados, el percentil i se calcula como:
{P}_{i}={L}_{i}+c\cdot \frac{\frac{i}{100}\cdot N-{F}_{i}}{{f}_{i}}
Donde:
- {P}_{i} es el percentil i
- {L}_{i} es el límite inferior de la clase del percentil
- c es la amplitud de la clase
- N es el total de datos
- {F}_{i} y {f}_{i} son la frecuencia absoluta acumulada y frecuencia absoluta de la clase mediana
Calculamos la frecuencia absoluta acumulada de los datos.
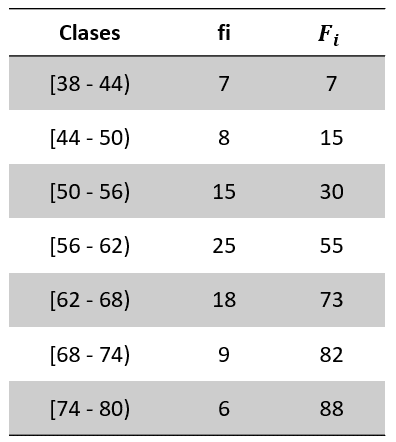
Calculamos la posición frecuencia absoluta acumulada que deberá tener la clase del percentil 40.
{F}_{40}=40\cdot \frac{88}{100}=35.2
La clase con una frecuencia absoluta acumulada menor o igual a 35.2 es \left[50-56\right) . El límite inferior {L}_{i}=50 , la amplitud es c=6 , la frecuencia absoluta es {f}_{i}=25 y la acumulada {F}_{i}=30 . Sustituimos todos los valores.
{P}_{40}=50+6\cdot \frac{35.2-30}{25}=57.25
El percentil 40 del conjunto de datos es igual a 57.25.
La respuesta correcta es el inciso a).
Reactivo 40
Los datos que se muestran en el siguiente histograma de frecuencias, parecen tener una distribución de tipo:
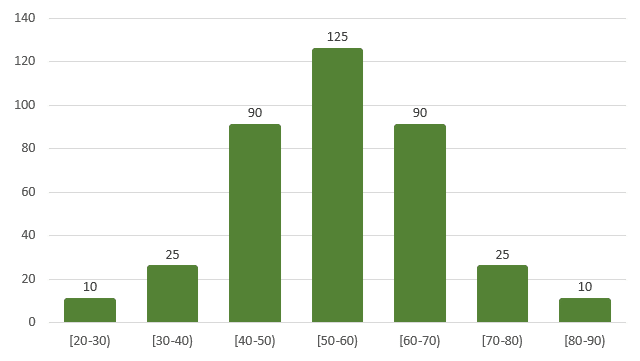
- Bernoulli
- Poisson
- Normal
Solución:
Para responder a la pregunta, debemos recordar cómo son las distribuciones de los incisos. La distribución de Bernoulli es una distribución de probabilidades discreta, donde los valores pueden encontrarse en una u otra clasificación.
La distribución de Poisson es también discreta y se aplica para sucesos de difícil ocurrencia. No tiene una forma definida, ya que esta depende de un parámetro \lambda . Finalmente, la distribución normal tiene forma de campana, es simétrica y continua.
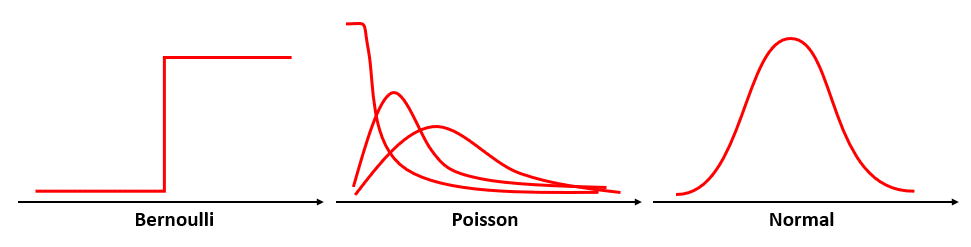
La respuesta correcta es el inciso c).

