Bienvenidos a la Parte 3 del Examen Simulador para el Exani II de Ceneval del módulo de probabilidad y estadística, en esta sección vamos a resolver los reactivos del 21 al 30.
¿Por qué es importante medir tu tiempo de respuesta? Recuerda que el objetivo no es solo responder correctamente, sino también hacerlo de manera eficiente (rápido).
Así que te sugerimos establecer un tiempo límite para cada reactivo, para que puedas evaluar tanto tu precisión como tu velocidad. Esto te proporcionará una experiencia de examen más realista y te ayudará a prepararte para las condiciones del día del examen de admisión.
Curso Exani II 2024
Reactivo 21
La probabilidad de dos eventos independientes A y B es: P\left(A\right)=0.25 y P\left(B\right)=0.3 . Calcule la probabilidad de la composición de ambos sucesos.
- 075
- 55
- 75
Solución:
En probabilidad, decimos que dos sucesos son independientes cuando la probabilidad de que uno ocurra no está condicionada, es independiente de la ocurrencia del otro. Como consecuencia de esto, la probabilidad compuesta se calcula mediante la regla de la multiplicación:
P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)
Sustituimos.
P\left(A\cap B\right)=\left(0.25\right)\left(0.3\right)=0.075
Comparando con los incisos, la respuesta correcta es a).
Reactivo 22
Se tiene el típico experimento de la urna llena con bolas de diferentes colores. Si en la urna hay: 5 bolas rojas, 3 bolas amarillas y 4 bolas azules, calcule la probabilidad de sacar una roja, luego una azul y luego una amarilla. Tenga en cuenta que no hay devolución.
- \frac{1}{22}
- \frac{3}{22}
- \frac{1}{11}
Solución:
Iniciamos realizando una representación gráfica mediante un diagrama de árbol para 3 extracciones.
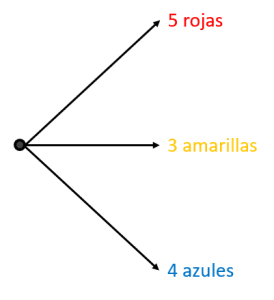
Segunda extracción. Tenemos tres bifurcaciones, una para cada probabilidad inicial.
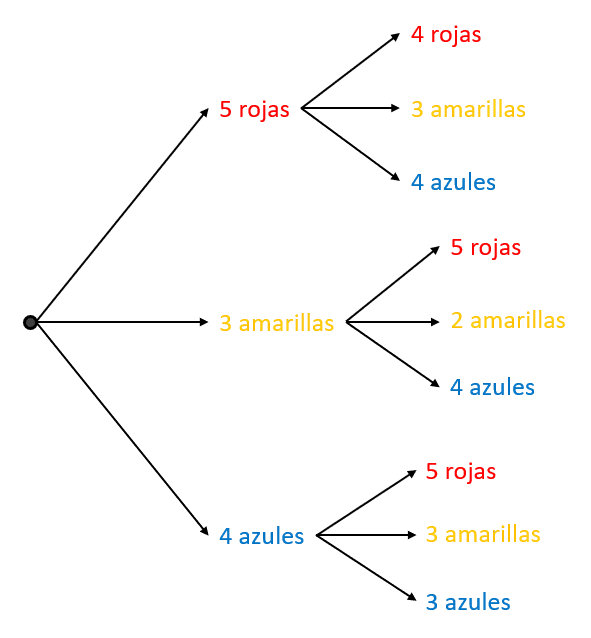
Tercera extracción. Solo haremos la ramificación para la rama superior que inicia con rojo y luego azul, ya que esa es la secuencia que nos interesa.
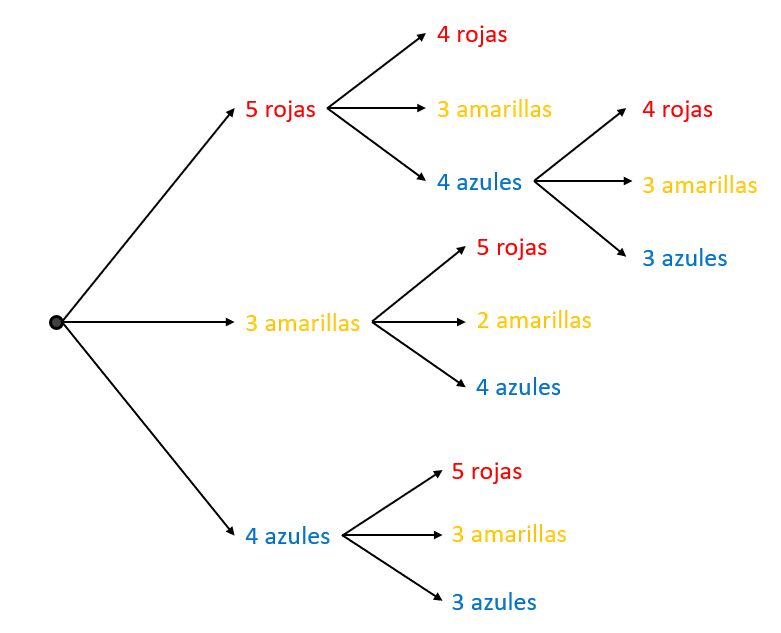
Resaltamos el camino con la secuencia rojo, azul y amarillo.
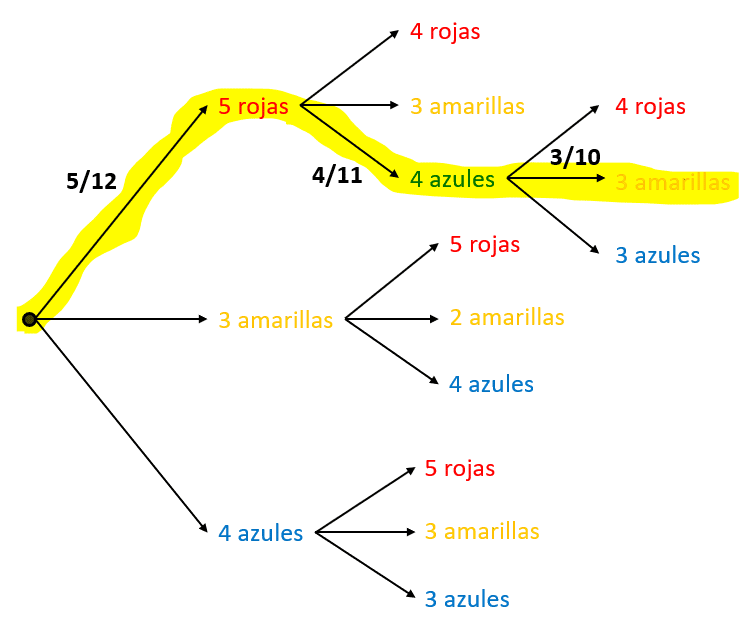
La probabilidad de sacar rojo, luego azul y luego amarillo se calcula mediante el principio multiplicativo.
\mathrm{P}\left(R,Az,Am\right)=\left(\frac{5}{12}\right)\left(\frac{4}{11}\right)\left(\frac{3}{10}\right)=\frac{1}{22}\approx 0.045
La respuesta correcta es el inciso a).
Reactivo 23
Un estudiante universitario va a presentar una prueba final de física que consta de 30 temas, pero él solo ha estudiado 25. En la prueba se escogen 3 temas al azar de los 30 disponibles. ¿Cuál es la probabilidad de que los tres sean conocidos para el estudiante?
- 566
- 324
- 034
Solución:
El problema nos solicita que calculemos la probabilidad de la intersección de 3 sucesos dependientes: contestar bien al tema 1, 2 y 3. La probabilidad de contestar bien a los tres temas se calcula como:
P\left({T}_{1}\cap {T}_{2}\cap {T}_{3}\right)=P\left({T}_{1}\right)\cdot P\left({T}_{2}/{T}_{1}\right)\cdot P\left({T}_{3}/{T}_{2}\cap {T}_{1}\right)
El primer factor corresponde a la probabilidad de contestar bien al primer tema. Al inicio, tenemos 25 temas a favor respecto a los 30 del examen.
P\left({T}_{1}\right)=\frac{25}{30}
El segundo factor corresponde a la probabilidad de contestar bien el segundo tema, una vez contestado bien el primero. Los casos a favor disminuyen a 24, mientras que el total a 29.
P\left({T}_{2}/{T}_{1}\right)=\frac{24}{29}
El último término corresponde a la probabilidad de contestar bien el tercero, una vez se ha contestado bien al primero y al segundo. Quedan 23 temas estudiados y 28 temas totales.
P\left({T}_{3}/{T}_{2}\cap {T}_{1}\right)=\frac{23}{28}
Sustituimos todo en la ecuación.
P\left({T}_{1}\cap {T}_{2}\cap {T}_{3}\right)=\left(\frac{25}{30}\right)\left(\frac{24}{29}\right)\left(\frac{23}{28}\right)=\frac{115}{203}\approx 0.566
Comparando con los incisos, concluimos que la respuesta correcta es el a).
Reactivo 24
En la final del mundial Alemania e Inglaterra deben decidir el ganador a través de una ronda de penales. Los dos últimos tiros de cada equipo los harán dos jugadores, el de Alemania tiene una efectividad de 2 goles cada 3 tiros y el de Inglaterra 3 goles cada 4 tiros.
¿Cuál es la probabilidad de que ambos acierten y tengan que ir a muerte súbita?
- \frac{2}{3}
- \frac{3}{4}
- \frac{1}{2}
Solución:
El que un jugador acierte o no el tiro, es independiente de que lo haga el otro. Por lo tanto, son eventos independientes si acierta el de Alemania o el de Inglaterra. Además, el enunciado nos dice cuál es la probabilidad de éxito para cada jugador.
Alemania.
\mathrm{P}\left(A\right)=\frac{2}{3}
Inglaterra.
P\left(I\right)=\frac{3}{4}
La probabilidad de que ambos acierten se calcula mediante la regla multiplicativa.
P\left(A\cap I\right)=\left(\frac{2}{3}\right)\left(\frac{3}{4}\right)=\frac{1}{5}=0.5
Indicamos como respuesta correcta al inciso c).
Reactivo 25
Una caja de las populares grageas de Harry Potter, tiene: 4 de naranja, 4 de tierra, 4 de césped y 4 de huevo podrido. ¿Cuál es la probabilidad de extraer, de forma consecutiva, las 4 grageas de naranja?
- Casi nula
- \frac{4}{16}
- \frac{3}{15}
Solución:
El total de grageas es igual a 16, al inicio hay 4 grageas de naranja, por tanto, la probabilidad de hacerlo en la primera es P\left(1\right)=\frac{4}{16}=\frac{1}{4} . En la segunda extracción, la probabilidad es P\left(2\right)=\frac{3}{15}=\frac{1}{5} . Para la tercera es: P\left(3\right)=\frac{2}{14}=\frac{1}{7} . Finalmente, la probabilidad en la cuarta es: P\left(4\right)=\frac{1}{13} .
La probabilidad de extraer de forma consecutiva las 4 grageas de naranja se calcula como:
P\left(1\cap 2\cap 3\cap 4\right)=\left(\frac{1}{4}\right)\left(\frac{1}{5}\right)\left(\frac{1}{7}\right)\left(\frac{1}{13}\right)=0.00055
La probabilidad es casi nula.
Comparando con los incisos, la respuesta correcta es el a).
Reactivo 26
Las resistencias eléctricas de medio vatio hacia debajo de potencia, tienen un encapsulado pequeño en el que no se pueden grabar números para indicar el valor de resistencia que posee. En su lugar, se utiliza un código con franjas de colores como el que se muestra en la figura.
Existen presentaciones con 4, 5 (como en este caso) y 6 bandas. En el de 5 bandas, las 3 primeras indican el valor resistivo, la cuarta es un factor multiplicativo y la quinta la tolerancia del material (estas dos últimas no son relevantes). Se cuenta con un total de 10 colores para las 3 primeras bandas.
¿Cuántos valores resistivos se pueden representar agrupándolos de 3 en 3?
- 1000
- 3000
- 2500
Solución:
Debido a que las franjas de colores forman un código, el código de color de las resistencias, importa el orden en el que se colocan, por tanto, para contarlas, debemos emplear una variación/permutación.
No intervienen todos los elementos, ya que se agrupan de 3 en 3 y se permite repetir. Empleamos la fórmula de variaciones con repetición.
{\mathrm{V}\mathrm{R}}_{\mathrm{10,3}}={10}^{3}=1000
Se pueden formar 1000 códigos de colores distintos con 10 colores.
La respuesta correcta es el inciso a).
Examen simulador: Probabilidad y estadística
Reactivo 27
Dado el siguiente gráfico, indique cuál es la igualdad que representa la zona subrayada.
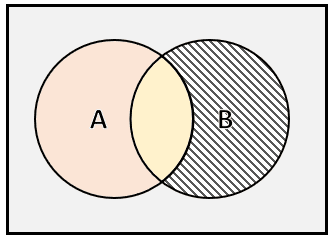
- B-A
- A-A\cap B
- A-B
Solución:
En la figura se encuentra señalada la región que pertenece al conjunto B y que no comparte ningún elemento con el conjunto A . Esto lo podemos representar mediante la diferencia de conjuntos:
B-A
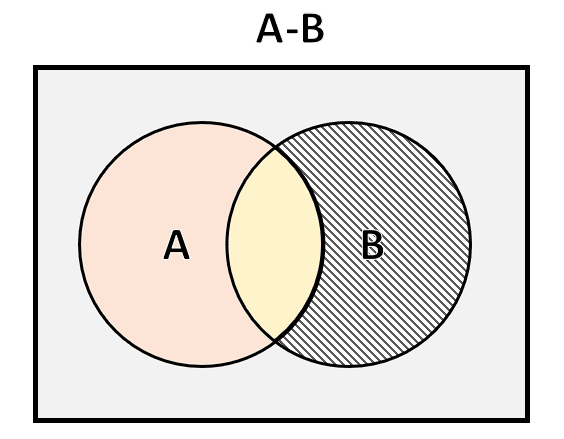
La respuesta correcta es el inciso a).
Reactivo 28
Para un conjunto m ordenado en grupos de n elementos, se sabe que la variación {\mathrm{V}}_{m, n}=20 y que la combinación {C}_{m, n}=10 . ¿Cuáles son los valores de m y n ?
- m=2, n=5
- m=5, n=2
- m=5, n=5
Solución:
De los temas referentes a las técnicas de conteo, sabemos que:
{V}_{m,n}=\frac{m!}{\left(m-n\right)!}
{C}_{m,n}=\frac{m!}{n!\left(m-n\right)!}
Debido a que trabajar con cantidades combinatorias sería un procedimiento extenso, vamos a ir probando los números de los incisos en las expresiones. Descartamos a los números del inciso a) porque m<n .
Inciso b).
{V}_{\mathrm{5,2}}=\frac{5!}{\left(5-2\right)!}=20
{C}_{\mathrm{5,2}}=\frac{5!}{2!\left(5-2\right)!}=\frac{20}{2\times 1}=10
Con este resultado, concluimos indicando que la respuesta correcta es el inciso b).
Reactivo 29
5 atletas olímpicos se encuentran disputando el podio en la última competición de salto. ¿De cuántas maneras se puede repartir el primer, segundo y tercer lugar entre los atletas?
- 65
- 62
- 60
Solución:
Debido a que no es igual que, por ejemplo, el atleta 1 sea el tercero o el primero, deducimos que importa el orden. Con esto, sabemos que debemos aplicar la fórmula de las permutaciones/variaciones.
No intervienen todos los elementos porque hay 3 lugares y 5 competidores. No se permiten repeticiones, porque un mismo atleta no puede ocupar dos lugares en el podio. Empleamos la ecuación de las variaciones ordinarias.
{V}_{\mathrm{5,3}}=\frac{5!}{\left(5-3\right)!}=60
El podio puede establecerse de 60 formas distintas.
La respuesta correcta es el inciso c).
Reactivo 30
El departamento de virología de un hospital, ha estimado que la probabilidad de que una persona llegue a emergencias contagiada con cierto virus es de P\left(V\right)=0.2 . Si durante ese mes el hospital contabilizó 1200 pacientes en emergencias, ¿cuántos estaban contagiados por el virus?
- 600
- 1000
- 240
Solución:
A partir de la fórmula de Laplace para calcular la probabilidad clásica, sabemos que la probabilidad de cualquier evento es igual a los sucesos favorables entre el total de sucesos. El enunciado nos da el total de pacientes y la probabilidad, podemos despejar a los pacientes contagiados.
P\left(V\right)=0.2=\frac{\mathrm{P}\mathrm{C}}{1200}
PC=\left(1200\right)\left(0.2\right)=240
El total de pacientes contagiados con el virus en ese mes fue de 240.
Indicamos como respuesta correcta al inciso c).
Hola, mi nombre es Fernando Toxqui y llevo más de una década como docente especializado en matemáticas, con un enfoque particular en la preparación para exámenes de admisión.
