Vamos a resolver la tercera parte de la guía de geometría analítica IPN 2023 que va desde el reactivo 21 hasta el 30.

Toma pausas entre grupo de reactivos, el descanso también forma parte del proceso de aprendizaje. Permítele a tu mente reflexionar sobre lo aprendido.
Reactivo 21
Dada la ecuación de la parábola (y-h)=r(x-k{)}^{2} , ¿qué valor determina si esta abre hacia arriba o hacia abajo?
- h
- k
- r
- x
Solución:
En la ecuación ordinaria de una parábola vertical, el parámetro que define la dirección de apertura (arriba o hacia abajo), es 4p .
Ecuación ordinaria de la parábola vertical.
4p\left(y-h\right)=(x-k{)}^{2}
La parábola abre hacia arriba si 4p>0 o abre hacia abajo si 4p<0 .
Comparando esto con la ecuación dada por el enunciado, tenemos que el parámetro 4p es equivalente a \frac{1}{r} .
\left(y-h\right)=r(x-k{)}^{2}\to \frac{1}{r}(y-h)=(x-k{)}^{2}
Por lo tanto, es el signo de r el que establece la dirección de la parábola.
Concluimos el problema indicando como respuesta correcta al inciso c).
Reactivo 22
Calcular el vértice y el foco de la parábola (x-9{)}^{2}=-6(y+5) .
- V\left(\mathrm{9,5}\right),F(\mathrm{9,13}/2)
- V\left(\mathrm{9,4}\right),F(9, 15/2)
- V(9,-5),F(9,-13/2)
- V(9,-4),F(9,-15/2)
Solución:
Para determinar el vértice y el foco de una parábola, iniciamos determinando la dirección en la que abre. Debido a que el parámetro 4p=-6 , es decir: negativo, la parábola se abre verticalmente hacia abajo.
Recordando que:
{\left(x-h\right)}^{2}=4p\left(y-k\right)
Sabemos por inspección que las coordenadas del vértice son: V\left(9, -5\right) . Por otra parte, el foco debe encontrarse por debajo del vértice debido a que abre hacia abajo. Las coordenadas del foco se calculan como:
F\left(h, k+p\right)
El valor de p lo extraemos de la ecuación.
4p=-6\to p=-\frac{3}{2}
Sustituyendo:
F\left(9, -5-\frac{3}{2}\right)\to F\left(9, -\frac{13}{2}\right)
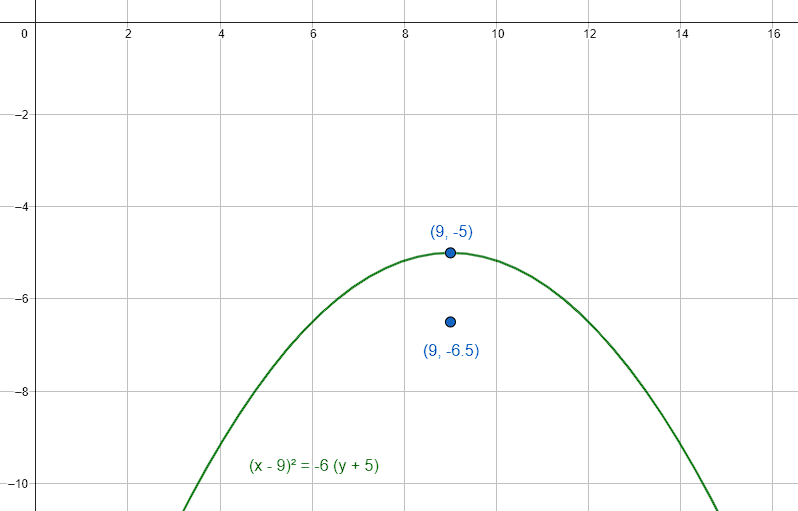
Concluimos indicando como respuesta correcta al inciso c).
Reactivo 23
Determinar la longitud del lado recto (LR) de la parábola con vértice V\left(\mathrm{5,4}\right) y foco F\left(\mathrm{5,2}\right) .
- 16
- 12
- 8
- 4
Solución:
Esta pregunta la podemos responder fácilmente con la fórmula para calcular las coordenadas del foco. Debido a que la coordenada x permanece constante entre el foco y el vértice, concluimos que se trata de una parábola que se abre verticalmente.
F\left(h, k+p\right)
Nos quedamos con la coordenada y del punto.
k+p=2
Sustituimos el valor de k .
4+p=2\to p=-2
Finalmente, calculamos el lado recto como:
LR=\left|4p\right|=\left|4(-2)\right|=8
El lado recto de la parábola, que tiene como vértice V\left(\mathrm{5,4}\right) y foco F\left(\mathrm{5,2}\right) , es de 8 unidades.
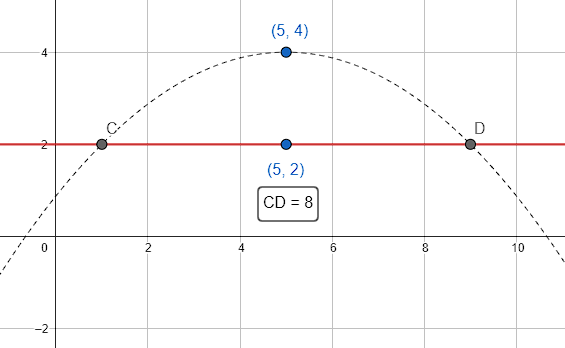
Concluimos que la respuesta correcta es el inciso c).
Conoce la oferta académica completa del Instituto Politécnico Nacional: Lista de carreras del IPN por área.
Reactivo 24
Determinar la excentricidad de la elipse
\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=25- \frac{\sqrt{7}}{4}
- \sqrt{\frac{7}{4}}
- \frac{\sqrt{7}}{2\sqrt{2}}
- \sqrt{\frac{7}{2}}
Solución:
Nota: en este reactivo hay un error en los incisos.
La excentricidad de una elipse se calcula como el cociente entre su semidistancia focal y el semieje mayor.
e=\frac{c}{a}=\sqrt{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}}
Simplificamos la ecuación de la elipse para obtener el valor de a y b .
\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=25
La ecuación debe estar igualada a 1, por tanto, dividimos todo entre 25.
\frac{{x}^{2}}{100}+\frac{{y}^{2}}{75}=1
{a}^{2}=100, {b}^{2}=75
Sustituimos en la ecuación de la excentricidad.
e=\sqrt{\frac{100-75}{100}}=\sqrt{\frac{1}{4}}
Hay un error en los incisos. La guía indica que la respuesta correcta es la b), pero esta excentricidad es mayor a 1, la excentricidad de una elipse se encuentra acotada e=\left[0, 1\right] .
Conoce los pasos para aplicar a la universidad: Todo sobre la convocatoria del IPN.
Reactivo 25
Dada la ecuación de la hipérbola, determinar su excentricidad.
4{x}^{2}-8x-9{y}^{2}+18y=41
- \frac{\sqrt{13}}{9}
- \frac{\sqrt{13}}{3}
- \frac{\sqrt{13}}{4}
- \frac{\sqrt{13}}{5}
Solución:
La excentricidad de una hipérbola, es igual al cociente entre la semi distancia focal y el semieje mayor.
e=\frac{c}{a}=\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}
Ahora, la tarea es encontrar el valor de a y b a partir de la forma general de la hipérbola. Acá podemos hacer dos cosas: completar cuadrados o aplicar alguna fórmula que relaciones a los coeficientes de la forma general con a y b .
Emplearemos el segundo camino, pero te queda como tarea aplicar el otro. Teniendo en cuenta los coeficientes de {x}^{2} y {y}^{2} :
{b}^{2}=4
-{a}^{2}=-9\to {a}^{2}=9
Sustituimos en la ecuación de la excentricidad.
e=\sqrt{1+\frac{4}{9}}=\sqrt{\frac{9+4}{9}}=\frac{\sqrt{13}}{3}
La excentricidad de la hipérbola es igual a \frac{\sqrt{13}}{3} .
Comparando con los incisos, indicamos a la opción b) como la respuesta correcta.
Reactivo 26
Encontrar la forma ordinaria de la ecuación de la elipse 9{x}^{2}+16{y}^{2}-144=0 .
- \frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}=-1
- \frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}=1
- \frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}=-1
- \frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}=1
Solución:
Debemos aplicar operaciones algebraicas hasta llegar a la forma ordinaria. Iniciamos enviando al término independiente al segundo miembro y dividiendo por 9 y 16.
9{x}^{2}+16{y}^{2}=144\to \frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}=\frac{144}{16\cdot 9}
Finalmente:
\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}=\frac{144}{144}\to \frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}=1
Concluimos indicando como respuesta correcta al inciso d).
Reactivo 27
Identificar la ecuación que corresponde a la siguiente gráfica:

- 4(x-2{)}^{2}+9(y+2{)}^{2}=144
- 9(x-2{)}^{2}+4(y+2{)}^{2}=144
- 9(x+2{)}^{2}+4(y-2{)}^{2}=144
- 4(x+2{)}^{2}+9(y-2{)}^{2}=144
Solución:
La ecuación ordinaria de una elipse con semieje mayor horizontal es:
\frac{{\left(x-h\right)}^{2}}{{a}^{2}}+\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1
Examinando la gráfica, extraemos las coordenadas del centro.
C\left(-2, 2\right)
Por otra parte, el semieje mayor y menor son:
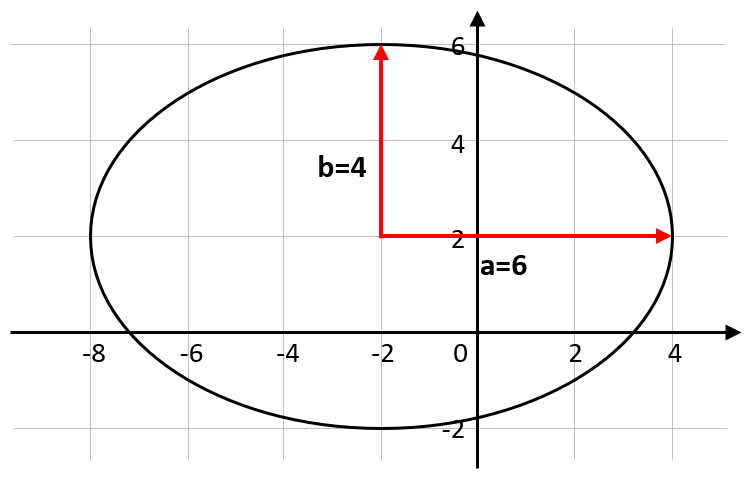
Sustituimos.
\frac{{\left(x+2\right)}^{2}}{{6}^{2}}+\frac{{\left(y-2\right)}^{2}}{{4}^{2}}=1\to \frac{{\left(x+2\right)}^{2}}{36}+\frac{{\left(y-2\right)}^{2}}{16}=1
Multiplicamos toda la expresión por 9 y 4.
\frac{{\left(x+2\right)}^{2}}{36}+\frac{{\left(y-2\right)}^{2}}{16}=1\to 16{\left(x+2\right)}^{2}+36{\left(y-2\right)}^{2}=576
Finalmente:
{4\left(x+2\right)}^{2}+{9\left(y-2\right)}^{2}=144
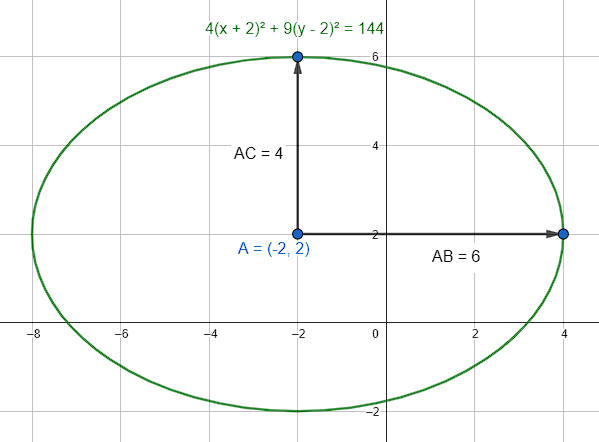
La respuesta correcta es el inciso d).
¿Sabes cuántos puntos necesitas para quedar? Conoce los aciertos por carrera del IPN.
Reactivo 28
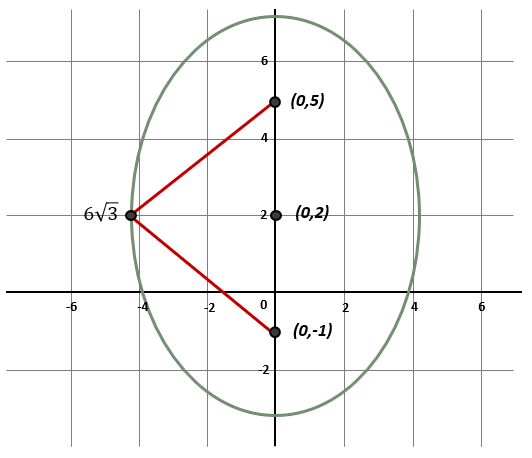
Elegir la ecuación de la elipse cuya suma de las distancias de un punto a los focos es 6\sqrt{3} , considerando que dichas distancias son iguales:
- \frac{(y-2{)}^{2}}{18}-\frac{{x}^{2}}{27}=1
- \frac{{y}^{2}}{27}-\frac{(x-2{)}^{2}}{18}=1
- \frac{(y-2{)}^{2}}{27}+\frac{{x}^{2}}{18}=1
- \frac{{y}^{2}}{18}+\frac{(x-2{)}^{2}}{27}=1
Solución:
Para resolver este problema, debemos utilizar la ecuación del lugar geométrico de la elipse.
d\left(P,{F}_{1}\right)+d\left(P,{F}_{2}\right)=2a
Donde 2a es una constante positiva y mayor que la distancia entre los focos. Si la suma de las distancias es 6\sqrt{3} entonces:
2a=6\sqrt{3}\to a=3\sqrt{3}
Este es el valor del semieje mayor.
Ahora, podemos calcular la semi distancia focal a partir de la imagen como la mitad de la distancia entre los focos.
c=\frac{d\left({F}_{1},{F}_{2}\right)}{2}=\frac{6}{2}=3
Con este resultado y apoyados en el triángulo rectángulo que se forma entre a , b y c , podemos calcular al semieje menor aplicando el teorema de Pitágoras.
b=\sqrt{{a}^{2}-{c}^{2}}=\sqrt{27-9}=\sqrt{18}
Finalmente, el centro de la elipse es \left(h, k\right)=\left(\mathrm{0,2}\right) , Sustituimos todo en la ecuación ordinaria de la elipse vertical y nos queda:
\frac{{\left(x-h\right)}^{2}}{{b}^{2}}+\frac{{\left(y-k\right)}^{2}}{{a}^{2}}=1\to \frac{{\left(x-0\right)}^{2}}{18}+\frac{{\left(y-2\right)}^{2}}{27}=1
Finalmente:
\frac{{x}^{2}}{18}+\frac{{\left(y-2\right)}^{2}}{27}=1
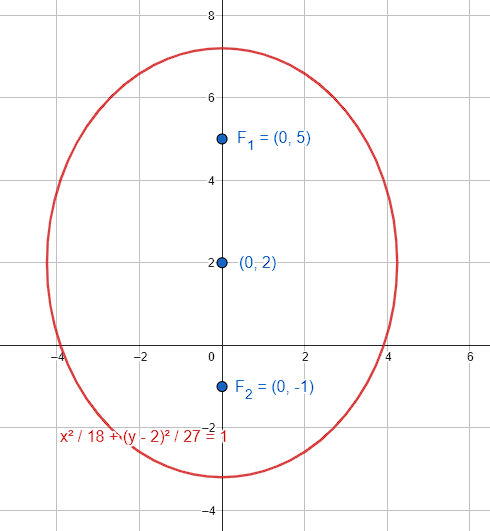
Concluimos indicando como respuesta correcta al inciso c).
Reactivo 29
La _______ es el lugar geométrico de los puntos en el plano donde la diferencia de sus distancias a dos puntos fijos es igual a una constante.
- elipse
- parábola
- hipérbola
- circunferencia
Solución:
Para responder esta pregunta, es necesario que conozcas previamente la descripción del lugar geométrico de las 4 cónicas. El enunciado anterior describe el lugar geométrico de la hipérbola.
\left|\left|FP\right|-\left|{F}^{\text{'}}P\right|\right|=2a
La respuesta correcta es el inciso c).
La hipérbola es el lugar geométrico de los puntos en el plano donde la diferencia de sus distancias a dos puntos fijos es igual a una constante.
Reactivo 30
Calcular el semieje mayor (a), semieje menor (b) y focos {F}_{1}\text{ y }{F}_{2} de la elipse
\frac{{x}^{2}}{625}+\frac{{y}^{2}}{400}=1
- a=25,b=20,{F}_{1}=\left(\mathrm{15,0}\right),{F}_{2}=\left(-\mathrm{15,0}\right)
- a=75,b=20,{F}_{1}=\left(0,-15\right),{F}_{2}=\left(\mathrm{0,15}\right)
- a=35,b=20,{F}_{1}=\left(\mathrm{15,0}\right),{F}_{2}=\left(-\mathrm{15,0}\right)
- a=55,b=20,{F}_{1}=\left(0,-15\right),{F}_{2}=\left(\mathrm{0,15}\right)
Solución:
Iniciamos identificando que se trata de una elipse con eje focal horizontal, debido a que el semieje de mayor tamaño se encuentra dividiendo a la variable x . Esto quiere decir que las coordenadas de los focos son:
{F}_{\mathrm{1,2}}=\left(h\pm c, k\right)
Donde c es la semidistancia focal y se calcula como:
c=\sqrt{{a}^{2}-{b}^{2}}
Examinando la ecuación, sabemos que: {a}^{2}=625 , {b}^{2}=400 y \left(h, k\right)=\left(0, 0\right) . Sustituimos los valores de {a}^{2} y {b}^{2} en la ecuación de c .
c=\sqrt{625-400}=\sqrt{225}=15
Por tanto, las coordenadas de los focos son:
{F}_{1}=\left(15, 0\right), {F}_{2}=\left(-15, 0\right)
Finalmente:
a=\sqrt{625}=25
b=\sqrt{400}=20
a=25,b=20,{F}_{1}=\left(\mathrm{15,0}\right),{F}_{2}=\left(-\mathrm{15,0}\right)
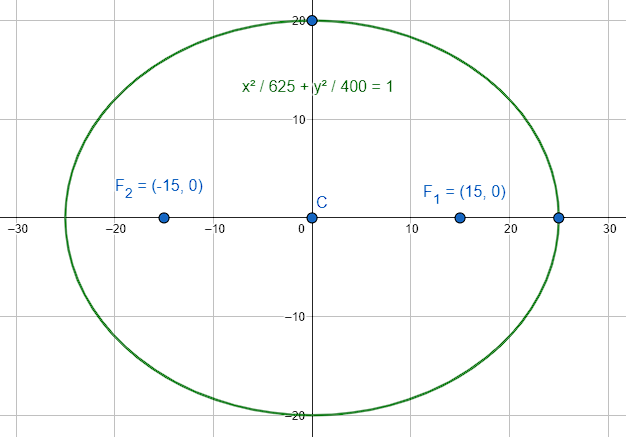
La respuesta correcta al problema se encuentra en el inciso a).


