Continuamos con la solución de la segunda parte de la guía de estudio IPN geometría analítica, desde el reactivo 11 al 20, como preparación al examen de ingreso.

Toma pausas entre grupo de reactivos, el descanso también forma parte del proceso de aprendizaje. Permítele a tu mente reflexionar sobre lo aprendido.
Reactivo 11
Determinar la forma simétrica de la ecuación de la recta que pasa por los puntos A\left(6,-2\right)\text{ y }B\left(-\mathrm{5,3}\right) .
- \frac{x}{\frac{8}{5}}+\frac{y}{\frac{8}{11}}=1
- y=-\frac{11}{4}x+\frac{5}{8}
- 4y=-9x-3
- 3x+4y-3=0
Solución:
Esta pregunta se puede responder con tan solo examinar los incisos. Recordemos que la ecuación simétrica de la recta es:
\frac{x}{a}+\frac{y}{b}=1
Donde a y b son los cortes con los ejes x y y respectivamente.
Teniendo en cuenta esto, la única opción que muestra una ecuación simétrica es la del inciso a). Sin embargo, vamos a realizar el cálculo para que puedas visualizar el procedimiento.
Debido a que el problema solo nos da dos puntos que pertenecen a la recta, iniciamos obteniendo la ecuación explícita de la recta. Calculamos la pendiente.
m=\frac{3+2}{-5-6}=-\frac{5}{11}
Sustituimos en la ecuación la pendiente y un punto, seleccionamos a A(6,-2) .
y+2=-\frac{5}{11}\left(x-6\right)\to y=-2+\frac{30}{11}-\frac{5}{11}x
y=\frac{8}{11}-\frac{5}{11}x
Despejamos y dividimos por el término independiente.
\frac{5}{11}x+y=\frac{8}{11}\to \frac{\frac{5}{11}x}{\frac{8}{11}}+\frac{y}{\frac{8}{11}}=1
Finalmente:
\frac{x}{\frac{8}{5}}+\frac{y}{\frac{8}{11}}=1
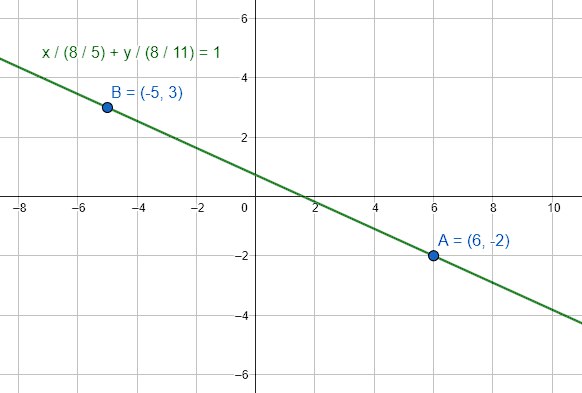
La respuesta correcta es el inciso a).
Reactivo 12
Calcular las ecuaciones correspondientes a la recta tangente en el punto (-\mathrm{3,3}) , ya la recta secante en el punto \left(\mathrm{1,3}\right) a la circunferencia (x+1{)}^{2}+(y-3{)}^{2}=4 cuando ambas se intersecan en el punto (-3,-1) .
- y=-3,y=x-2
- x=-3,y=x+2
- x=-3y,y=-x+2
- y=-3x,y=-x-2
Solución:
Analizando toda la información que nos proporciona el enunciado, sabemos que los puntos \left(-\mathrm{3,3}\right) y \left(-3,-1\right) pertenecen a la recta tangente, mientras que \left(-3, -1\right) y \left(1, 3\right) pertenecen a la recta secante. Solo debemos calcular la ecuación explícita de la recta en ambos casos.
Ecuación de la recta tangente.
Ambos puntos tienen la misma coordenada en x , esto significa que es una recta vertical en x=-3 .
x=-3
Ecuación de la recta secante.
{m}_{s}=\frac{3+1}{1+3}=1
Sustituimos cualquiera de los puntos en la ecuación punto pendiente. Seleccionamos \left(1, 3\right) .
y-3=\left(1\right)\left(x-1\right)\to y=x+2
Finalmente: x=-3 , y=x+2 .
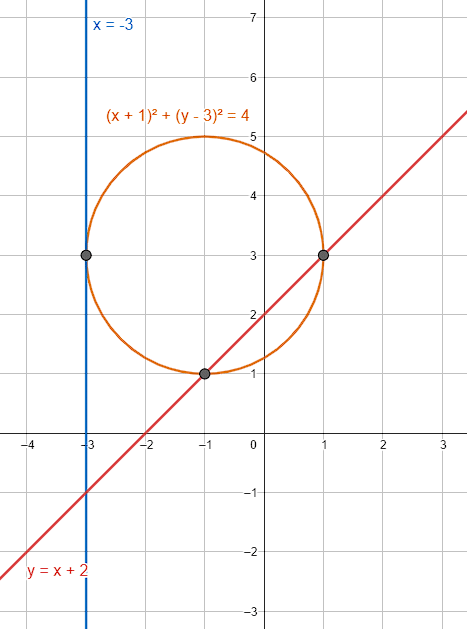
La respuesta correcta es el inciso b).
Reactivo 13
Asociar la ecuación con el tipo de cónica que le corresponde.

- 1D, 2C, 3B, 4A
- 1A, 2B, 3C, 4D
- 1D, 2A, 3C, 4B
- 1A, 2C, 3B, 4D
Solución:
Para responder esta pregunta, es necesario que conozcas de antemano las ecuaciones relacionadas a cada una de las cónicas. Teniendo en cuenta lo anterior: la primera ecuación representa a una circunferencia de radio r y centrada en \left(h, k\right) ; 1D.
La segunda ecuación pertenece a una elipse vertical centrada en \left(h, k\right) . Es vertical, porque el semieje mayor a está dividiendo a la y . Entonces: 2A. Con esta información: 1D, 2A, … tenemos para concluir que la respuesta correcta es el inciso c).
Reactivo 14
Calcular las coordenadas del centro y la longitud del radio de la circunferencia
{x}^{2}+{y}^{2}+10x-14y+10=0
- C\left(5,-7\right)\text{ y }r=8
- C\left(\mathrm{5,7}\right)\text{ y }r=\sqrt{10}
- C\left(-5,-7\right)\text{ y }r=\sqrt{10}
- C(-5, 7)\text{ y }r=8
Solución:
Para calcular las coordenadas del centro y el radio de la circunferencia, debemos completar cuadrados para ambas variables: x y y . Al completar cuadrados, convertimos a un trinomio de la forma {x}^{2}+bx+c en un trinomio cuadrado perfecto: {\left(x+d\right)}^{2}\pm e .
Agrupamos a los términos con la misma variable.
{x}^{2}+10x+{y}^{2}-14y+10=0
A los términos lineales tenemos que descomponerlos en bx=2dx , de esta forma identificamos el término independiente del trinomio cuadrado perfecto.
{x}^{2}+2\left(5\right)x+{y}^{2}-2\left(7\right)y+10=0
Para la variable x {d}_{x}=5 , mientras que la y , {d}_{y}=7 . Debemos sumar en ambos miembros de la igualdad el cuadrado de {d}_{x} y {d}_{y} .
{x}^{2}+10x+25+{y}^{2}-14y+49=49+25-10
Completamos cuadrado.
{\left(x+5\right)}^{2}+{\left(y-7\right)}^{2}=64
Finalmente:
{\left(x+5\right)}^{2}+{\left(y-7\right)}^{2}={8}^{2}
El centro de la circunferencia es \left(-5, 7\right) y el radio r=8 .
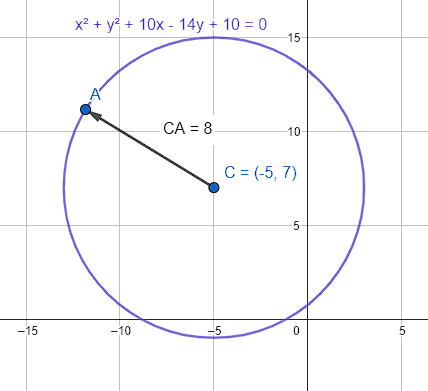
La respuesta correcta es el inciso d).
Reactivo 15
Identificar la ecuación circunferencia con centro \left(\frac{3}{2},-2\right) radio r=\sqrt{\sqrt{2}} .
- (2x-3{)}^{2}+4(y-2{)}^{2}=2\sqrt{2}
- (2x-3{)}^{2}+4(y+2{)}^{2}=4\sqrt{2}
- (2x-3{)}^{2}+4(y+2{)}^{2}=4\sqrt{\sqrt{2}}
- (2x-3{)}^{2}+4(y-2{)}^{2}=2\sqrt{\sqrt{2}}
Solución:
Debemos sustituir el valor del radio y centro en la ecuación ordinaria de la circunferencia.
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
Sustituyendo nos queda:
{\left(x-\frac{3}{2}\right)}^{2}+{\left(y+2\right)}^{2}={\left(\sqrt{\sqrt{2}}\right)}^{2}\to {\left(\frac{2x-3}{2}\right)}^{2}+{\left(y+2\right)}^{2}=\sqrt{2}
\frac{{\left(2x-3\right)}^{2}}{4}+{\left(y+2\right)}^{2}=\sqrt{2}\to {\left(2x-3\right)}^{2}+4{\left(y+2\right)}^{2}=4\sqrt{2}
Finalmente, la circunferencia que tiene por radio r=\sqrt{\sqrt{2}} y centro \left(\frac{3}{2},-2\right) es:
{\left(2x-3\right)}^{2}+4{\left(y+2\right)}^{2}=4\sqrt{2}
Concluimos el problema seleccionando la opción b) como la respuesta correcta.
Reactivo 16
Relacionar la ecuación de la circunferencia con su centro.

- 1C, 2B, 3A, 4D
- 1A, 2D, 3C, 4B
- 1A, 2B, 3C, 4D
- 1C, 2D, 3A, 4B
Solución:
En este caso, vamos a completar cuadrados en las ecuaciones que sea necesario.
Primera circunferencia.
{x}^{2}+{y}^{2}-4x+6y-23=0
{x}^{2}-4x+{y}^{2}+6y=23
Descomponemos a los coeficientes de los términos lineales.
{x}^{2}-2\left(2\right)x+{y}^{2}+2\left(3\right)y=23
Sumamos en ambos miembros {2}^{2}=4 y {3}^{2}=9 .
{x}^{2}-2\left(2\right)x+4+{y}^{2}+2\left(3\right)y+9=23+13
Aplicamos la fórmula del trinomio cuadrado perfecto.
{\left(x-2\right)}^{2}+{\left(y+3\right)}^{2}=36
El centro de esta primera circunferencia es \left(2, -3\right) . Por lo tanto: 1C. Descartamos los incisos b y c.
Segunda circunferencia.
{x}^{2}+{\left(y-5\right)}^{2}-25=0
El centro de la circunferencia 2 lo extraemos de forma directa: \left(0, 5\right) . Por tanto: 2D. Esta información: 1C, 2D, … podemos concluir que la respuesta correcta es el inciso d).
Reactivo 17
Determinar las coordenadas del centro de la circunferencia con ecuación:
{x}^{2}+{y}^{2}+5x-6y+\frac{61}{4}=25
- \left(\frac{5}{2},3\right)
- \left(-\frac{5}{2},-3\right)
- \left(\frac{5}{2},-3\right)
- \left(-\frac{5}{2},3\right)
Solución:
En este caso podríamos completar cuadrados para resolver el problema, pero en su lugar, aplicaremos la siguiente ecuación para encontrar el centro de la circunferencia dada su ecuación general.
{x}^{2}+{y}^{2}+Dx+Ey+F=0
c\left(-\frac{D}{2}, -\frac{E}{2}\right)
Examinando la circunferencia del enunciado, tenemos que:
D=5, E=-6
Sustituyendo:
c\left(-\frac{5}{2},\frac{6}{2}\right)=c\left(-\frac{5}{2}, 3\right)
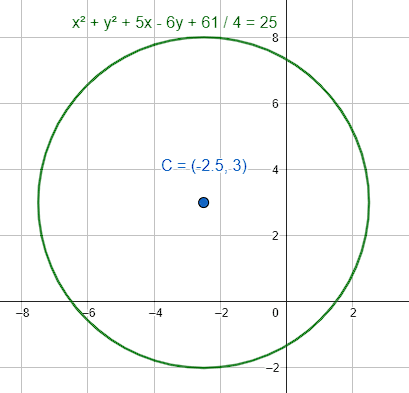
Concluimos que la respuesta correcta es el inciso d).
Reactivo 18
Determinar el vértice de la parábola de siguiente ecuación:
y=-{x}^{2}+2x+99
- \left(\mathrm{1,100}\right)
- \left(-\mathrm{1,100}\right)
- \left(1,-100\right)
- \left(-1,-100\right)
Solución:
Para encontrar el vértice de la parábola, debemos completar cuadrados respecto a la variable x . Iniciamos pasando al 99 al primer miembro.
y-99=-{x}^{2}+2x
Debemos restar 1 en ambos miembros para aplicar el trinomio cuadrado perfecto.
y-99-1=-{x}^{2}+2x-1
Simplificamos y extraemos al menos factor común.
y-100=-\left({x}^{2}-2x+1\right)
Finalmente:
y-100=-{\left(x-1\right)}^{2}
El vértice de la parábola es: \left(h,k\right)=\left(1, 100\right) .
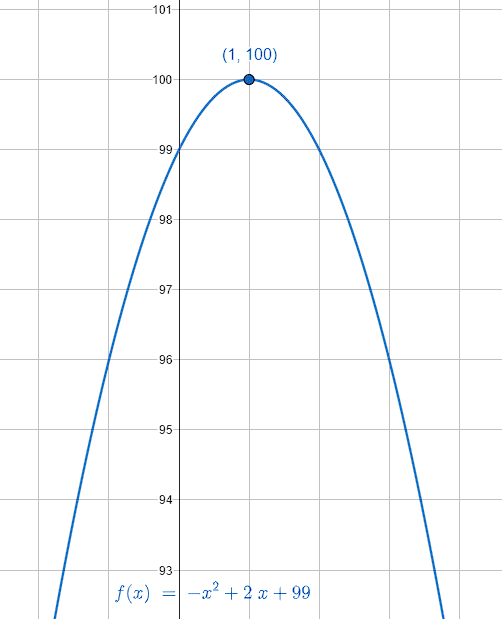
La respuesta correcta es el inciso a).
Reactivo 19
Calcular la ecuación de la circunferencia circunscrita en el triángulo rectángulo formado por las rectas x=0,y=0,y=x+4 , cuya intersección de medianas es el centro (h,k) .
- (x-2{)}^{2}+(y+2{)}^{2}=(\sqrt{2}{)}^{2}
- (x+2{)}^{2}+(y-2{)}^{2}={2}^{2}
- (x+2{)}^{2}+(y-2{)}^{2}=(2\sqrt{2}{)}^{2}
- (x+2{)}^{2}+(y+2{)}^{2}=(2{)}^{2}
Solución:
Iniciamos graficando las rectas indicadas en el enunciado. La recta x=0 es vertical, la recta y=0 es una recta horizontal y y=x+4 es una recta oblicua de pendiente 1.
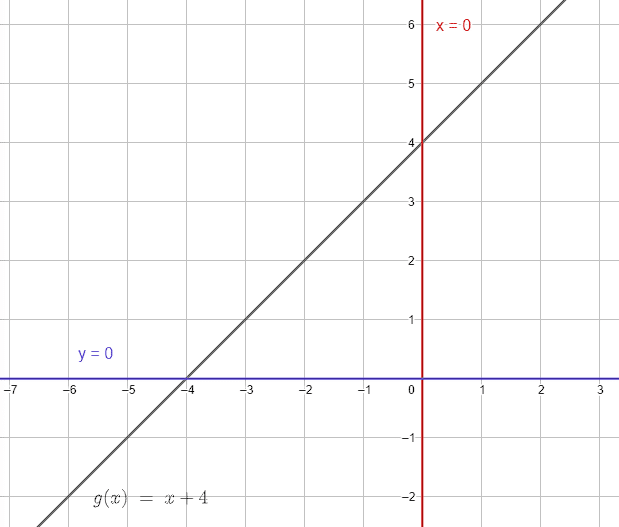
Cuando la circunferencia está circunscrita en un triángulo rectángulo, se cumple que la longitud de la hipotenusa es igual al diámetro y el centro es igual al punto medio de la hipotenusa.
A partir del gráfico, sabemos que los vértices del triángulo son:
{V}_{1}\left(-4, 0\right), {V}_{2}\left(0, 0\right), {V}_{3}\left(0, 4\right)
Los vértices de la hipotenusa son: {V}_{1}\left(-4, 0\right) y {V}_{3}\left(0, 4\right) .
Calculamos el centro aplicando la ecuación del punto medio de un segmento:
C\left(-\frac{4}{2},\frac{4}{2}\right)=C\left(-2, 2\right)
La longitud de la hipotenusa la calculamos aplicando Pitágoras. Los catetos miden 4 unidades cada uno.
D=\sqrt{{4}^{2}+{4}^{2}}=\sqrt{32}
El radio sería:
r=\frac{\sqrt{32}}{2}=\frac{4\sqrt{2}}{2}=2\sqrt{2}
Finalmente, sustituimos el resultado en la ecuación ordinaria de la circunferencia.
{\left(x+2\right)}^{2}+{\left(y-2\right)}^{2}={\left(2\sqrt{2}\right)}^{2}
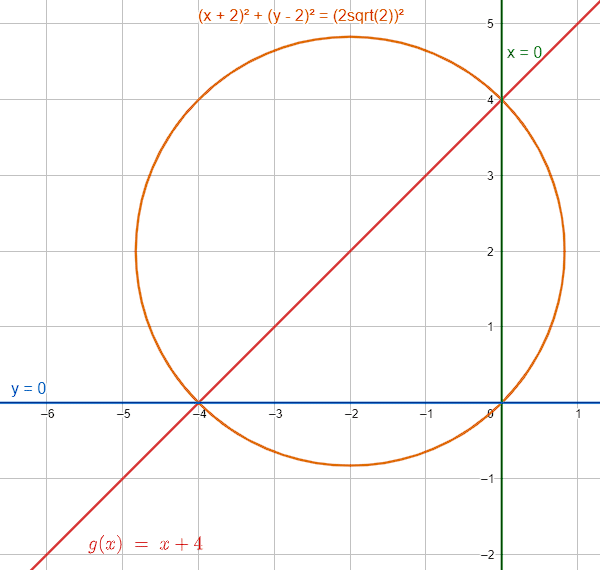
Concluimos que la respuesta correcta es el inciso c).
Reactivo 20
Identificar la ecuación de la parábola con vértice en (2,-1) y foco en (2,-1/2) .
- 2y={x}^{2}-4x+2
- 2y={x}^{2}-4x+3
- 2y={x}^{2}+2x-3
- 2y={x}^{2}-2x+2
Solución:
Examinando las coordenadas del vértice y el foco, vemos que este último se encuentra por encima del vértice, esto significa que es una parábola vertical y que abre hacia arriba.
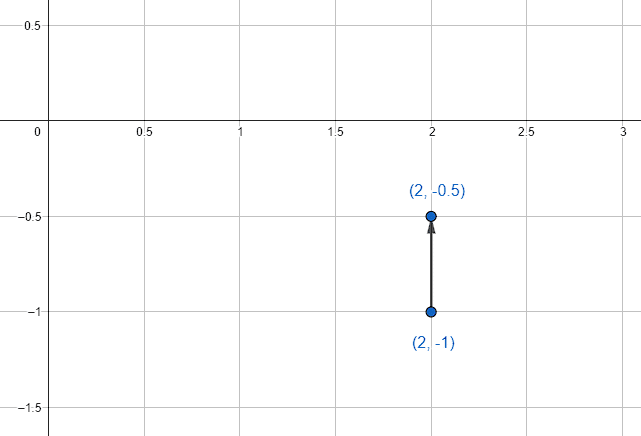
La ecuación de una parábola vertical y que abre hacia arriba es:
{\left(x-h\right)}^{2}=4p\left(y-k\right)
Donde \left(h,k\right) es el vértice y p es el lado recto de la parábola. El lado recto p es igual a la distancia entre el vértice y el foco.
p=d\left(V, F\right)=\sqrt{{\left(-1+\frac{1}{2}\right)}^{2}}=\frac{1}{2}
Sustituimos todos los valores en la expresión.
{\left(x-2\right)}^{2}=4\left(\frac{1}{2}\right)\left(y+1\right)\to {x}^{2}-4x+4=2y+2
2y={x}^{2}-4x+2
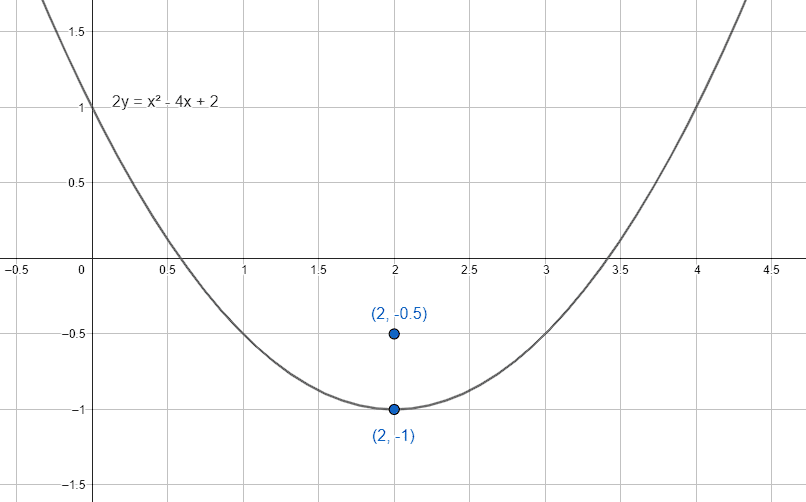
Finalmente, la respuesta correcta es el inciso a).

