Llegamos a la cuarta y última parte de la guía de estudio IPN 2023, geometría analítica. En este caso, resolveremos los reactivos comprendidos entre el 31 y el 40.
Puedes continuar estudiando para el examen de ingreso con el resto de material gratuito resuelto que tenemos en la zona IPN.
Conoce el curso que cubre todos los temas del nuevo examen de ingreso al IPN con clases en vivo y exámenes simulacro.
Reactivo 31
Asociar la ecuación con el tipo de cónica que le corresponde.
- 1A, 2B, 3C, 4D
- 1B, 2C, 3D, 4A
- 1A, 2B, 3D, 4C
- 1B, 2D, 3C, 4A
Solución:
Para resolver este problema, debes conocer de antemano la forma que tienen las ecuaciones de las cónicas. Vamos a ir examinando las ecuaciones en la columna izquierda para relacionarlas con los nombres en la columna derecha.
Primera ecuación.
{x}^{2}+{y}^{2}=9
Esta es la ecuación de una circunferencia centrada en el origen y con radio igual a 3. Para este caso: 1B. Descartamos los incisos a y c.
Segunda ecuación.
{x}^{2}-{y}^{2}=9\to \frac{{x}^{2}}{9}-\frac{{y}^{2}}{9}=1
Esta es la ecuación de una hipérbola, por lo tanto: 2C. Con la información que tenemos hasta este punto: 1B, 2C, … Concluimos que la respuesta correcta es el inciso b).
Reactivo 32
Señalar las coordenadas de los vértices y focos de la siguiente hipérbola.
\frac{(x-3{)}^{2}}{25}-\frac{{y}^{2}}{45}=1
- \begin{array}{c}{\mathrm{v}}_{1}\left(\mathrm{8,0}\right);\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{F}}_{1}(3+\sqrt{70},0)\\ {\mathrm{v}}_{2}\left(\mathrm{2,0}\right):\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{F}}_{2}(3-\sqrt{70},0)\end{array}
- \begin{array}{c}{\mathrm{v}}_{1}(-\mathrm{8,0});\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{F}}_{1}(3+\sqrt{70},0)\\ {\mathrm{v}}_{2}\left(\mathrm{2,0}\right):\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{F}}_{2}(3-\sqrt{70},0)\end{array}
- \begin{array}{c}{\mathrm{v}}_{1}\left(\mathrm{8,0}\right); {\mathrm{F}}_{1}(3+\sqrt{70},0)\\ {\mathrm{v}}_{1}\left(-\mathrm{2,0}\right); {\mathrm{F}}_{2}(3-\sqrt{70},0)\end{array}
- \begin{array}{c}{\mathrm{v}}_{1}\left(\mathrm{8,0}\right);\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{F}}_{1}(-3+\sqrt{70},0)\\ {\mathrm{v}}_{2}\left(\mathrm{2,0}\right):\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{F}}_{2}(-3-\sqrt{70},0)\end{array}
Solución:
Para obtener las coordenadas de los vértices y los focos, iniciamos identificando el tipo de hipérbola que representa. Debido a que la coordenada y es la negativa, tenemos que es una hipérbola con eje focal horizontal.
Los vértices se calculan como:
{V}_{\mathrm{1,2}}\left(h\pm a,k\right)
Donde \left(h, k\right) son las coordenadas del centro y a es la raíz cuadrada del divisor de x . Examinando la ecuación de la hipérbola: C\left(3, 0\right) y a=5 .
Coordenadas de los vértices.
{V}_{12}\left(3\pm 5, 0\right)\to \begin{array}{c}{V}_{1}\left(8, 0\right)\\ {V}_{2}\left(-2, 0\right)\end{array}
Si buscamos esta combinación en los incisos, la única que indica este resultado para los vértices es el c). En la solución del examen, en este punto puedes dar por concluido el ejercicio. Vamos a calcular los focos para que conozcas cuál es el procedimiento.
Los focos se calculan como:
{F}_{\mathrm{1,2}}\left(h\pm c, k\right)
Donde c es la hipotenusa del triángulo que forman a y b .
c=\sqrt{{a}^{2}+{b}^{2}}
Sustituimos.
c=\sqrt{25+45}=\sqrt{70}
Finalmente:
{F}_{\mathrm{1,2}}\left(3\pm \sqrt{70}, 0\right)
Conoce los pasos para aplicar a la universidad: Todo sobre la convocatoria del IPN.
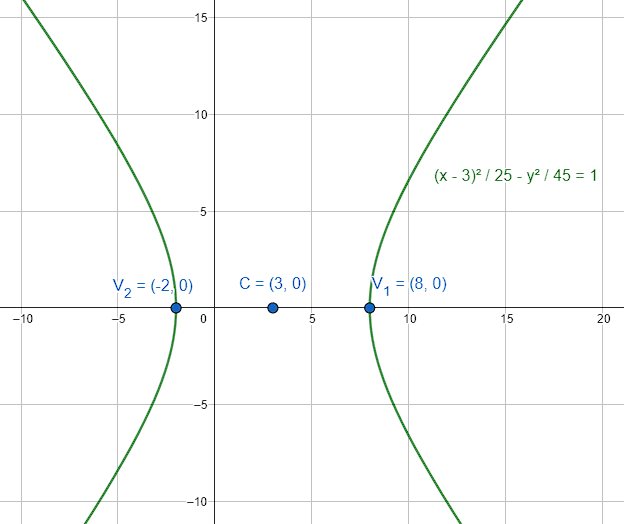
Reactivo 33
Encontrar la forma canónica de la siguiente ecuación:
25{x}^{2}-4{y}^{2}+100=0
- \frac{{y}^{2}}{25}-\frac{{x}^{2}}{4}=-1
- \frac{{y}^{2}}{25}-\frac{{x}^{2}}{4}=1
- \frac{{y}^{2}}{25}+\frac{{x}^{2}}{4}=-1
- \frac{{y}^{2}}{25}+\frac{{x}^{2}}{4}=1
Solución:
Iniciamos llevando al término independiente al segundo miembro, para luego dividir por los coeficientes de las variables.
25{x}^{2}-4{y}^{2}+100=0\to 25{x}^{2}-4{y}^{2}=-100
4{y}^{2}-25{x}^{2}=100
Dividimos por los coeficientes.
\frac{{y}^{2}}{25}-\frac{{x}^{2}}{4}=\frac{100}{4\cdot 25}\to \frac{{y}^{2}}{25}-\frac{{x}^{2}}{4}=1
Es la ecuación de una hipérbola vertical.
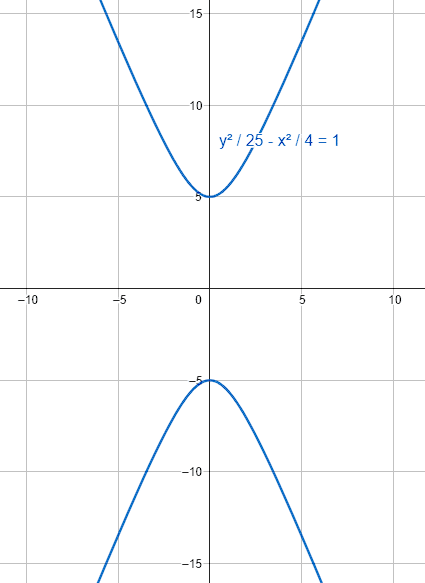
Concluimos indicando como respuesta correcta al inciso b).
Sigue practicando la parte de geometría analítica:
Reactivo 34
Determinar la ecuación de la hipérbola, con vértices \mathrm{V}=(\pm \mathrm{5,0})\text{ y }\mathrm{e}=\frac{4}{3} .
- 9{x}^{2}-7{y}^{2}=175
- 7{x}^{2}-9{y}^{2}=175
- 9{x}^{2}-7{y}^{2}=125
- 7{x}^{2}-9{y}^{2}=125
Solución:
Este problema tiene un detalle muy interesante. Resulta que el valor del parámetro a lo podemos extraer de los vértices, ya que este es igual a la mitad de la distancia entre ellos, es decir a=5 en esta ocasión.
Por otro lado, la excentricidad es igual al cociente entre c y a . Si intentamos extraer el valor de a y c a partir de la excentricidad veremos que:
c=4, a=3
El valor de a es aparentemente menor al calculado a partir de los vértices.
Esto realmente se debe a que extrayendo los valores de la fracción, estamos obteniendo los mínimos valores de a y c que la satisfacen. Existe infinidad de valores de a y c que la satisfacen. Por ello, a partir de la excentricidad debemos calcular a b .
e=\frac{4}{3}=\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}
Sustituyendo el valor de a .
\frac{4}{3}=\frac{\sqrt{25+{b}^{2}}}{5}
Resolviendo esta ecuación obtendremos el valor real de b .
\sqrt{25+{b}^{2}}=\frac{20}{3}\to 25+{b}^{2}=\frac{400}{9}
\therefore {b}^{2}=\frac{175}{9}
Con el valor de {a}^{2}=25 , {b}^{2}=\frac{175}{9} y C\left(0, 0\right) , podemos calcular la ecuación de la hipérbola. Sabemos que el centro es el origen porque los vértices tienen el mismo valor en x pero con signo opuesto.
Por otra parte, al encontrarse en la horizontal los vértices sabemos que se trata de una hipérbola horizontal:
\frac{{\left(x-h\right)}^{2}}{{a}^{2}}-\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1
Sustituimos todo.
\frac{{x}^{2}}{25}-\frac{{y}^{2}}{\frac{175}{9}}=1
Desarrollamos.
{x}^{2}-25\frac{{y}^{2}}{\frac{175}{9}}=25\to {x}^{2}-\frac{9}{7}{y}^{2}=25
\therefore 7{x}^{2}-9{y}^{2}=175
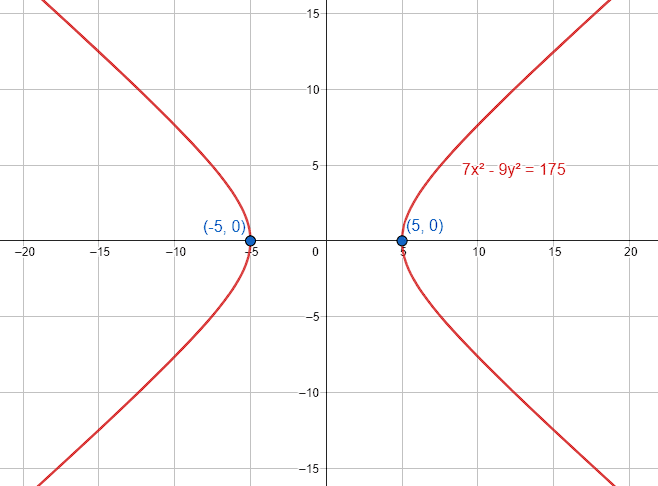
La respuesta correcta es el inciso b).
Conoce la oferta académica completa del Instituto Politécnico Nacional: Lista de carreras del IPN por área.
Reactivo 35
¿Qué longitudes tienen los semiejes de la hipérbola?
\frac{{x}^{2}}{9}-\frac{{y}^{2}}{25}=1
- a=2\text{ y }b=5
- a=3\text{ y }b=5
- a=9\text{ y }b=5
- a=3\text{ y }b=10
Solución:
En la hipérbola, el cuadrado del semieje a se encuentra dividiendo a la variable positiva, mientras que el cuadrado del semieje b divide a la variable negativa. Llevando esto a la hipérbola del enunciado, tenemos que:
{a}^{2}=9\to a=3
{b}^{2}=25\to 5
Finalmente:
a=3\text{ y }b=5
La respuesta correcta es el inciso b).
Reactivo 36
Expresar la ecuación de la recta en coordenadas polares.
y=4x+3
- r=4r\mathrm{cot}\left(\theta \right)+3\mathrm{csc}\left(\theta \right)
- r=4r\mathrm{tan}\left(\theta \right)+3\mathrm{csc}\left(\theta \right)
- r=4r\mathrm{cot}\left(\theta \right)+3\mathrm{sec}\left(\theta \right)
- r=4r\mathrm{tan}\left(\theta \right)+3\mathrm{sec}\left(\theta \right)
Solución:
Para transformar cualquier expresión de coordenadas rectangulares a coordenadas polares, tenemos las siguientes igualdades.
\left\{\begin{array}{c}x=r\mathrm{cos}\theta \\ y=r\mathrm{sin}\theta \end{array}\right.
Aplicando la transformación en la igualdad nos queda:
r\mathrm{sin}\theta =4r\mathrm{cos}\theta +3
Dividimos todo entre seno.
r=\frac{4r\mathrm{cos}\theta }{\mathrm{sin}\theta }+\frac{3}{\mathrm{sin}\theta }
r=4r\mathrm{cot}\theta +3\mathrm{csc}\theta
Comparando con los incisos, indicamos como respuesta correcta a la opción a).
¿Sabes cuántos puntos necesitas para quedar? Conoce los aciertos por carrera del IPN.
Reactivo 37
Señalar las coordenadas rectangulares del punto P\left(\sqrt{12},{60}^{\circ }\right) en el plano.
- x=-\sqrt{3},y=3
- x=\sqrt{3},y=-3
- x=-\sqrt{3},y=-3
- x=\sqrt{3},y=3
Solución:
Al transformar coordenadas polares a cartesianas, aplicamos las siguientes ecuaciones.
\left\{\begin{array}{c}x=r\mathrm{cos}\theta \\ y=r\mathrm{sin}\theta \end{array}\right.
Desde este momento podemos concluir que la respuesta es el inciso d), porque según el ángulo dado, el punto debe encontrarse en el primer cuadrante. Región del plano en el que ambas coordenadas son positivas. Sin embargo, vamos a realizar el cálculo paso a paso.
Sustituimos.
\left\{\begin{array}{c}x=\sqrt{12}\mathrm{cos}60\\ y=\sqrt{12}\mathrm{sin}60\end{array}\right.=\left\{\begin{array}{c}x=\sqrt{12}\mathrm{cos}60\\ y=\sqrt{12}\mathrm{sin}60\end{array}\right.=\left\{\begin{array}{c}x=\sqrt{12}\left(\frac{1}{2}\right)\\ y=\sqrt{12}\left(\frac{\sqrt{3}}{2}\right)\end{array}\right.
\left\{\begin{array}{c}x=\sqrt{\frac{12}{4}}\\ y=\sqrt{\frac{12\cdot 3}{4}}\end{array}\right.=\left\{\begin{array}{c}x=\sqrt{3}\\ y=\sqrt{9}\end{array}\right.=\left\{\begin{array}{c}x=\sqrt{3}\\ y=3\end{array}\right.
Las coordenadas del punto son: P\left(\sqrt{3}, 3\right) .
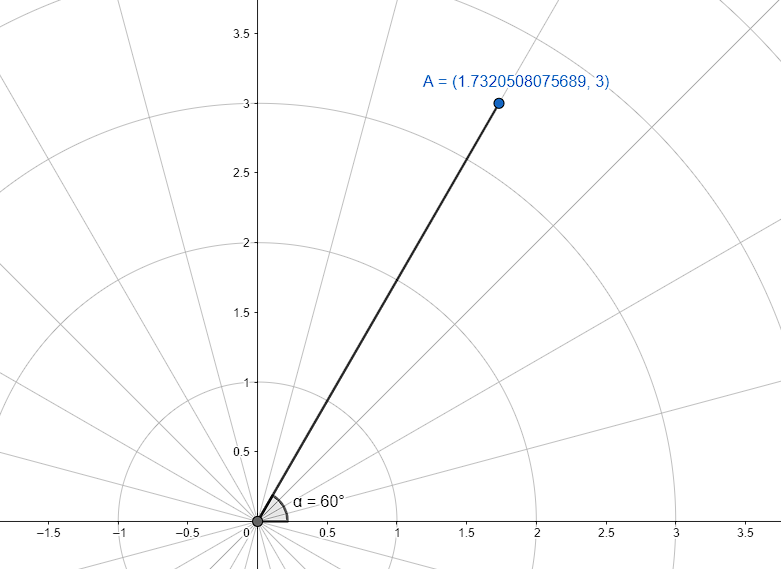
La respuesta correcta es el inciso d).
Reactivo 38
Identificar las coordenadas polares del punto (2, -2) en el plano.
- r=\sqrt{2};\theta ={300}^{\circ }
- r=2\sqrt{2};\theta ={315}^{\circ }
- r=\sqrt{2};\theta ={60}^{\circ }
- r=2\sqrt{2};\theta ={45}^{\circ }
Solución:
Examinando las coordenadas, sabemos que el punto se encuentra en el cuarto cuadrante. Esto quiere decir que el ángulo debe estar entre 270° y 360°, por lo tanto, descartamos a los incisos c y d.
Podemos concluir el reactivo con sólo calcular la longitud de r .
r=\sqrt{{x}^{2}+{y}^{2}}
Sustituyendo:
r=\sqrt{{2}^{2}+{\left(-2\right)}^{2}}=\sqrt{4+4}=2\sqrt{2}
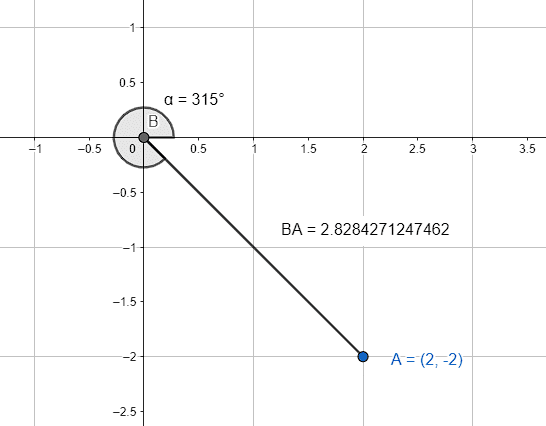
La respuesta correcta es el inciso b).
Reactivo 39
Las ecuaciones:
\begin{array}{c}x=2+6cos\left(\theta \right)\\ y=-4+6sen\left(\theta \right)\end{array}
para 0\le \theta \le 2\pi corresponden a la parametrización de una:
- recta
- elipse
- hipérbola
- circunferencia
Solución:
En este tipo de reactivos, debemos eliminar las identidades trigonométricas. Nuestra principal herramienta es la identidad pitagórica.
{\mathrm{cos}}^{2}\left(\theta \right)+{\mathrm{s}\mathrm{in}}^{2}\left(\theta \right)=1
Iniciamos elevando al cuadrado ambas ecuaciones.
x=2+6\mathrm{cos}\left(\theta \right)\to x-2=6\mathrm{cos}\left(\theta \right)
{\left(x-2\right)}^{2}=36{\mathrm{cos}}^{2}\left(\theta \right)\to \frac{{\left(x-2\right)}^{2}}{36}={\mathrm{cos}}^{2}\left(\theta \right)
y=-4+6\mathrm{sen}\left(\theta \right)\to y+4=6\mathrm{sen}\left(\theta \right)
{\left(y+4\right)}^{2}=36{\mathrm{sen}}^{2}\left(\theta \right)\to \frac{{\left(y+4\right)}^{2}}{36}={\mathrm{sen}}^{2}\left(\theta \right)
Sumamos ambas ecuaciones.
\frac{{\left(x-2\right)}^{2}}{36}+\frac{{\left(y+4\right)}^{2}}{36}={\mathrm{cos}}^{2}\left(\theta \right)+{\mathrm{sen}}^{2}\left(\theta \right)
\frac{{\left(x-2\right)}^{2}}{36}+\frac{{\left(y+4\right)}^{2}}{36}=1\to {\left(x-2\right)}^{2}+{\left(y+4\right)}^{2}=36
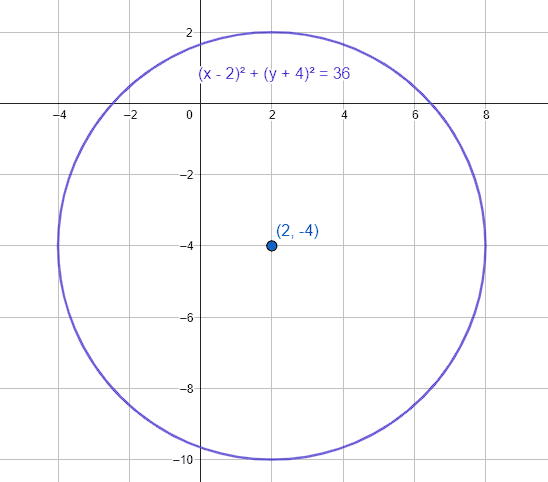
Esta es la ecuación de una circunferencia centrada en \left(2, -4\right) y de radio r=6 .
Indicamos al inciso d) como la respuesta correcta.
Reactivo 40
Identificar las ecuaciones paramétricas de la circunferencia con centro (1, -3) que pasa por el punto P (4, 1).
- \left\{\begin{array}{c}x=-1+3cos\left(\theta \right)\\ y=3+3sen\left(\theta \right)\end{array}\right.
- \left\{\begin{array}{c}x=1-4cos\left(\theta \right)\\ y=3+4sen\left(\theta \right)\end{array}\right.
- \left\{\begin{array}{c}x=1+5cos\left(\theta \right)\\ y=-3+5sen\left(\theta \right)\end{array}\right.
- \left\{\begin{array}{c}x=1+6cos\left(\theta \right)\\ y=-3-6sen\left(\theta \right)\end{array}\right.
Solución:
Este reactivo lo podemos resolver de dos formas: obteniendo la ecuación de la circunferencia a partir de las ecuaciones paramétricas o, calcular la ecuación paramétrica a partir de la ecuación de la circunferencia.
Vamos a aplicar la segunda opción. La ecuación de la circunferencia sería:
{\left(x-1\right)}^{2}+{\left(y+3\right)}^{2}=25
Dividimos todo entre 25.
\frac{{\left(x-1\right)}^{2}}{25}+\frac{{\left(y+3\right)}^{2}}{25}=1
Sustituimos al 1 por la identidad pitagórica.
\frac{{\left(x-1\right)}^{2}}{25}+\frac{{\left(y+3\right)}^{2}}{25}={\mathrm{cos}}^{2}\left(\theta \right)+{\mathrm{sen}}^{2}\left(\theta \right)
Parametrizamos a x con el coseno y a y con el seno.
\frac{{\left(x-1\right)}^{2}}{25}={\mathrm{cos}}^{2}\left(\theta \right)
\frac{{\left(y+3\right)}^{2}}{25}={\mathrm{sen}}^{2}\left(\theta \right)
Despejamos a las variables.
\left\{\begin{array}{c}\frac{{\left(x-1\right)}^{2}}{25}={\mathrm{cos}}^{2}\left(\theta \right)\\ \frac{{\left(y+3\right)}^{2}}{25}={\mathrm{sen}}^{2}\left(\theta \right)\end{array}\right.\to \left\{\begin{array}{c}{\left(x-1\right)}^{2}=25{\mathrm{cos}}^{2}\left(\theta \right)\\ {\left(y+3\right)}^{2}=25{\mathrm{sen}}^{2}\left(\theta \right)\end{array}\right.\to \left\{\begin{array}{c}x-1=5\mathrm{cos}\left(\theta \right)\\ y+3=5\mathrm{sen}\left(\theta \right)\end{array}\right.
Finalmente:
\left\{\begin{array}{c}x=5\mathrm{cos}\left(\theta \right)+1\\ y=5\mathrm{sen}\left(\theta \right)-3\end{array}\right.
Concluimos que la respuesta correcta es el inciso c).
