Examen Simulador IPN: Probabilidad y Estadística del 21 al 30

Para la tercera parte del examen simulacro de probabilidad y estadística, vamos con los ejercicios del 21 al 30 de matemáticas para el examen de admisión al IPN.

No olvides medir tu tiempo al momento de contestar los reactivos por tu cuenta. Recuerda que en el examen no basta con hacerlo bien, también debes hacerlo en el tiempo límite indicado.

Reactivo 21

Un vendedor de paletas le propone a un cliente un trato. El vendedor lanzará al aire dos monedas y al mismo tiempo el cliente lanzará también una moneda al aire, esto se repetirá ocho veces. Si cae dos veces águila le regalará una paleta, en caso contrario el cliente cubrirá el costo sin paleta. Con base al espacio muestral ¿Cuántas veces podría ganar el vendedor?

1. 3
2. 4
3. 5
4. 6

Solución:

Extrayendo del problema todo el enunciado, básicamente el experimento aleatorio se basa en lanzar al aire 3 monedas juntas ocho veces. Los posibles resultados con:

S=\{A A A, A A C, A C A, A C C, C A A, C A C, C C A, C C C\}

En este caso, solo nos interesa el evento en el que no sale águila dos veces por tanto, el subconjunto de este evento en particular sería:

S_{1}=\{A C C, C A C, C C A, C C C, A A A\}

Es decir, el vendedor tiene 5 oportunidades en las cuales, no sale águila dos veces. Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).

Reactivo 22

En un experimento se lanzan dos dados, se define la variable X  como la suma de los números que aparece en los dados ¿Cuántos posibles resultados constituyen el espacio muestral de la variable X ?

1. 6
2. 11
3. 12
4. 36

Solución:

Para dar respuesta al ejercicio, primero construiremos el espacio muestral de lanzar los dos dados a la vez.

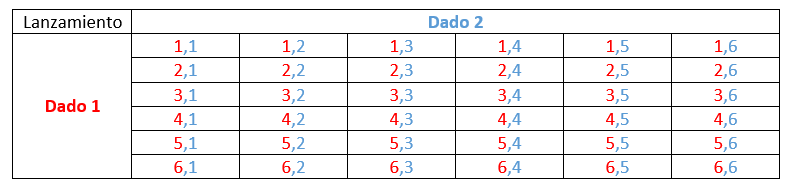
El espacio muestral es de 36 elementos o pares ordenados con los posibles resultados en las dos caras de los dados lanzados. Ahora, sumemos los posibles resultados para determinar el espacio muestral de X .

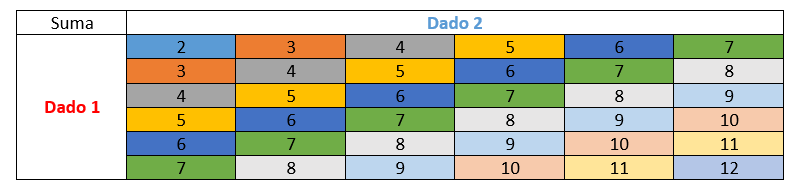
La suma de cada casilla se repite en diagonal y de la tabla podemos identificar 11 diagonales, es decir 11 números que son el resultado de sumar las caras de ambos lados.

X=\{2,3,4,5,6,7,8,9,10,11,12\}

El espacio muestral de X  tiene un tamaño de 11 elementos, por tanto la respuesta correcta es la b).

Reactivo 23

Se lanza una moneda y si aparece águila se lanza un dado y el experimento termina. Si aparece Sol se lanza la moneda una vez más. Seleccionar el espacio muestral del experimento.

1. A 1, A 2, A 3, A 4, A 5, A 6, A S, S S
2. S 1, S 2, S 3, S 4, S 5, S 6, S A, S S
3. A 1, A 2, A 3, A 4, A 5, A 6, S 1, S 2, S 3, S 4, S 5, S 6
4. A 1, A 2, A 3, A 4, A 5, A 6, S A, S S

Solución:

Para este problema, será conveniente realizar el diagrama de árbol porque brinda una perspectiva más clara de los eventos.

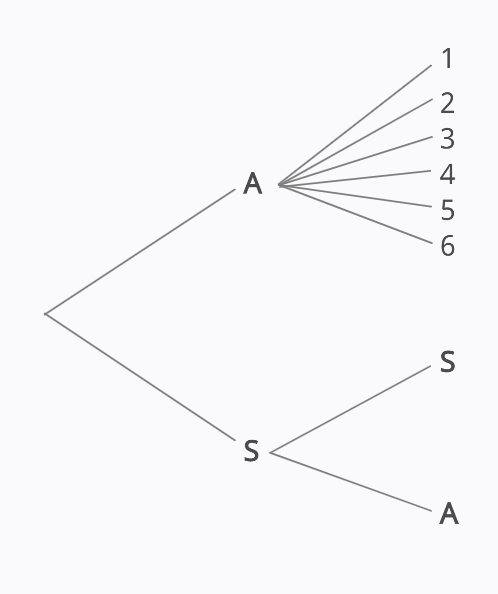
A partir del diagrama de árbol, podemos extraer el espacio muestral con todos los posibles eventos.

S=\{A 1, A, 2, A 3, A 4, A 5, A 6, S A, S S\}

Comprando con las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 24

Si  es el espacio muestral y A^{C} \cup A=S , expresar P(S)  en términos de P(A) \text { у } P\left(A^{C}\right) .

1. P(S)=P(A) \times P\left(A^{C}\right)
2. 1=P(A) \times P\left(A^{C}\right)
3. P(S)=P(A) \div P\left(A^{C}\right)
4. 1=P(A)+P\left(A^{C}\right)

Solución:

De la teoría de conjuntos, sabemos que A^{C} \cup A  da como resultado al conjunto universo, que en este caso corresponde al espacio muestral S de un experimento aleatorio.

La probabilidad del espacio muestral total es siempre 1 y si P(A)  es la probabilidad de un evento, P\left(A^{C}\right)  será la probabilidad del resto de eventos en S  que no son de A , por lo que la suma de ambas probabilidades es por definición la probabilidad de S , es decir 1.

P(A)+P\left(A^{C}\right)=1

Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 25

Se realizan análisis clínicos a los obreros de una fábrica. Se obtienen los siguientes datos: el 35% sufre de diabetes, el 45% padece hipertensión y el 20% sufre ambas afecciones. Si se escoge un obrero al azar, calcula la probabilidad de que no tenga alguna de estas enfermedades.

1. 60%
2. 45%
3. 40%
4. 35%

Solución:

Si analizamos el problema desde la perspectiva de la teoría de conjuntos, podríamos asegurar que los empleados con diabetes y con hipertensión representan a los conjuntos D \text { y } H , mientras que aquellos que padecen de ambas representan a la intersección de ambos conjuntos.

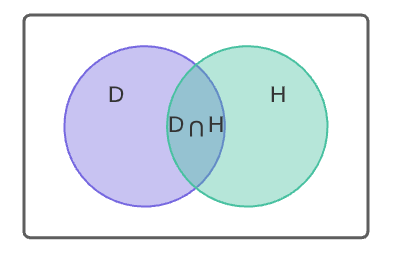
Al problema podremos resolverlo utilizando una de las reglas aditivas para eventos de un espacio muestral.

P(D \cup H)=P(D)+P(H)-P(D \cap H)

Nos interesa calcular la unión de ambos conjuntos, ya que el complemento de ese resultado son todos los empleados que no padecen ninguna de las dos enfermedades. Sería la zona blanca en el diagrama de Venn.

P(D \cup H)=35 \%+45 \%-20 \%

P(D \cup H)=60 \%

El complemento de un conjunto se calcula como:

P(D \cup H)^{c}=P(S)-P(D \cup H)

Ya que P(S)=100 \%  porque es el conjunto universo nos queda:

P(D \cup H)^{c}=100 \%-60 \%=40 \%

Concluimos que: el 40% de los empleados en la empresa no padecen ninguna enfermedad. Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).

Reactivo 26

Dados los eventos P\left(A^{c}\right)=3 / 4, P(B)=1 / 2, P(A \cap B)=1 / 8 \text { . Calcular } P(B \mid A) .

1. 1/8
2. 1/4
3. 1/2
4. 5/8

Solución:

La probabilidad condicionada de que un evento B  ocurra dado que ya ocurrió otro evento A  se calcula como:

P(A)=\frac{P(A \cap B)}{P(A)}

En este caso, el problema indica a P(A \cap B)  pero del evento A  solo conocemos la probabilidad de su complemento, del cual podemos calcular P(A)  gracias a que:

P(A)+P\left(A^{c}\right)=1

Entonces:

P(A)=1-P\left(A^{c}\right)=1-\frac{3}{4}=\frac{1}{4}

Sustituimos en la fórmula de probabilidad condicionada:

P(A)=\frac{\frac{1}{8}}{\frac{1}{4}}=\frac{1}{2}

Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).

Reactivo 27

Se tiene una bolsa con 10 dulces de chocolate, 8 de menta y 5 de limón. Si se extrae uno al azar, calcular la probabilidad de que este sea de menta.

1. 1/23
2. 8/23
3. 1/8
4. 1/4

Solución:

Para calcular la probabilidad de un suceso A, se realiza el cociente entre el número de casos favorables al suceso sobre el número total de casos posibles.

P(A)=\frac{C_{f}}{C_{t}}

Donde C_{f}  es el número de casos favorables al suceso \text { A y } C_{t}  es el número total de casos o espacio muestral total.

En el ejercicio, el suceso sería sacar un dulce de menta DM y la cantidad de casos favorables a ese suceso son 8 (la cantidad de dulces de menta). El espacio muestral total es la cantidad total de dulces en la bolsa, es decir D C+D L+D M=10+5+8=23 .

P(D L)=\frac{8}{23}

Comparando con las opciones que ofrece el problema, la opción correcta sería la b).

Reactivo 28

Una urna I  contiene dos esferas blancas y tres guindas, otra urna \text { II }  contiene cuatro esferas blancas y cuatro esferas guindas. Se selecciona una urna al azar y se elige una esfera al azar. Si la esfera resultante es blanca, calcular la probabilidad de que provenga de la urna I .

1. 1/5
2. 4/5
3. 4/9
4. 5/9

Solución:

Para resolver este problema, emplearemos la probabilidad condicionada, ya que debe ocurrir primero la escogencia entre las urnas, para luego sacar una esfera de la urna seleccionada. Lo anterior se visualiza mejor con un pequeño diagrama de árbol.

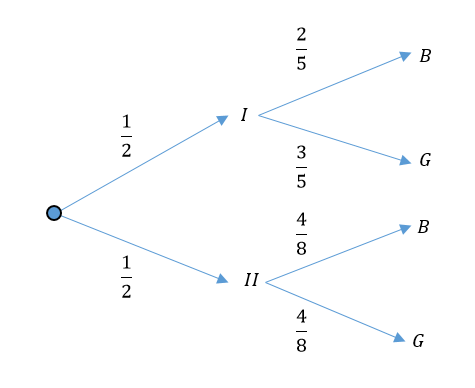
Donde B  representa a las esferas blancas y G  a las guindas. Finalmente, la probabilidad de sacar una esfera blanca de la urna I  es:

P(I \mid B)=\frac{P(I \cap B)}{P(B)}

Ya que I \text { y } B  son eventos independientes, su probabilidad conjunta es:

P(I \cap B)=P(I) P(B)=\frac{1}{2} \cdot \frac{2}{5}=\frac{1}{5}

La probabilidad marginal de B  es:

P(B)=P(B \cup I)+P(B \cup I I)=\frac{1}{5}+\frac{1}{2} \cdot \frac{1}{2}=\frac{9}{20}

Sustituyendo en la fórmula de P(I \mid B) :

P(I \mid B)=\frac{\frac{1}{5}}{\frac{9}{20}}=\frac{4}{9}

Concluimos que la probabilidad de escoger una esfera blanca y que provenga de la urna I \text { es } \frac{4}{9}  o 44.44%. Comparando con las opciones del problema, la respuesta correcta es la c).

Reactivo 29

Una caja contiene 6 billetes de $20, tres de $100 y uno de $500, todos los billetes son del mismo tamaño. Una persona puede extraer dos billetes de la caja y solo el segundo billete extraído se lo quedará. Los billetes se extraen de uno por uno y sin reemplazo ¿Cuál es la probabilidad de que en el segundo intento salga el billete de $500, dado que no salió antes?

1. 1/30
2. 1/15
3. 1/10
4. 1/9

Solución:

Debemos analizar con detenimiento la pregunta que se hace en el problema, nos solicitan la probabilidad de que en el segundo intento salga el billete de $500 dado que no salió antes, en probabilidad condicionada esto se escribiría:

P\left(B 500 \mid B 500^{c}\right)

Es decir, es la probabilidad condicionada del opuesto de un mismo evento y, por definición, ambos son mutuamente excluyentes, por tanto:

P\left(B 500 \mid B 500^{c}\right)=P(B 500)

En el segundo intento se quedan 9 billetes, porque del primero se ha extraído 1, por lo tanto, la probabilidad queda como:

P\left(B 500 \mid B 500^{c}\right)=\frac{1}{9}

Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 30

Se lanza un par de dados distinguibles, comunes y corrientes sobre una mesa, si la suma de los puntos de los dados es menor a siete, calcular la probabilidad de que ambos dados muestren números impares.

1. 1/5
2. 2/5
3. 3/5
4. 4/5

Solución:

Para resolver este problema, debemos aislar los números en las caras de ambos dados que sumados, dan como resultado un número menor que 7. En la siguiente imagen podemos visualizarlo.

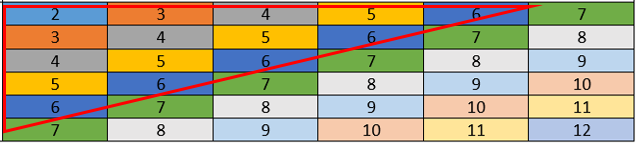
En total, son 15 los pares que suman menos de 7. Ahora, entre ellos solo debemos considerar aquellos que sean impares ambas caras.

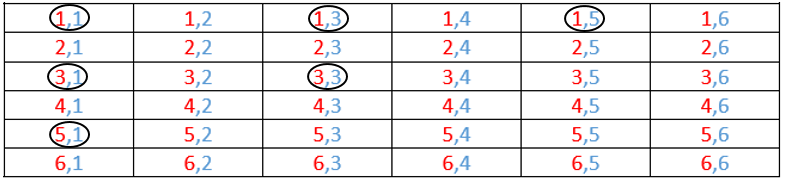
Son 6 los números que suman menos de 7 y que son ambos impares a la vez, por tanto:

P=\frac{6}{15}=\frac{2}{5}

Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).