Hola de nuevo, aspirante. ¿Cómo va tu nivel de conocimientos en matemáticas hasta ahora? Continuamos con los siguientes 10 reactivos de la parte 4 del examen simulacro de probabilidad y estadística para el examen de ingreso al IPN.

Ahora vamos a resolver los reactivos del 31 al 40. No olvides que este tema viene en el examen de admisión a todas las carreras.
Reactivo 31
Relacionar el evento con la descripción de manera correcta.
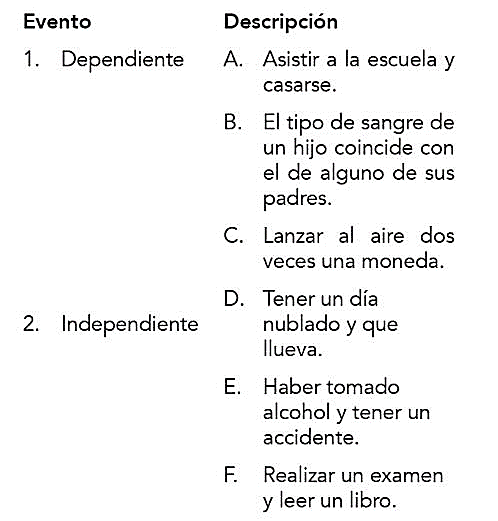
- 1BDF, 2ACE
- 1AED, 2BCF
- 1ACD, 2BEF
- 1BDE, 2ACF
Solución:
Para encontrar las relaciones correctas, analizaremos cada descripción en la columna derecha para asociarla con el tipo de evento probabilístico correcto.
A.
Evidentemente, asistir a la escuela y casarse no son eventos en la vida de una persona que dependen mutuamente. Es un caso de evento independiente.
B.
Por temas de biología básica, sabemos que el tipo de sangre que tendrá un bebe al nacer depende inequívocamente del tipo sanguíneo de su padre o madre. Por tanto, es un evento Dependiente.
C.
El resultado de lanzar al aire una moneda no tiene relación directa con haber sido lanzada antes. Es un evento igualmente aleatorio con dos posibilidades. Por tanto, es un evento independiente.
D.
Es bastante claro que, sin un cielo nublado no es posible que llueva. La lluvia es un evento Dependiente del cielo nublado.
E.
Consumir bebidas alcohólicas mientras se está al volante es una de las principales causas de accidentes viales al año. Por tanto, es un evento Dependiente.
F.
Leer un libro de cualquier temática y realizar un examen es un caso claro de eventos independientes.
Con todo analizado hasta este punto, la unión de todas las soluciones es:
1BDE y 2ACF
Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).
Reactivo 32
Se dice que R \text { y } Q son eventos independientes si P(R)=P(Q) , entonces P(R \cap Q) es igual a:
- P(Q)
- P(R \cup Q)
- P(Q) P(R)
- P(Q)+P(R)
Solución:
Si dos eventos son independientes, es claro que la operación P(R) que se lee como “la probabilidad de que ocurra Q , dado que ocurrió R ” sea igual a la probabilidad del evento Q , porque no depende en ninguna medida de R .
Ahora, si a este resultado lo igualamos a la expresión original de P(R) es decir \frac{P(R \cap Q)}{P(R)} nos queda que:
\frac{P(R \cap Q)}{P(R)}=P(Q)
Despejando a P(R \cap Q) .
P(R \cap Q)=P(Q) P(R)
Comparando con las opciones del problema, la respuesta correcta es la c).
Reactivo 33
Una fábrica emplea tres máquinas que hacen latas para empacar alimentos. Los porcentajes de latas que no cumplen con las especificaciones son: 5%, 8% y 3% respectivamente. Si se selecciona una lata al azar ¿Cuál es la probabilidad de que cumpla con las especificaciones?
- 4.8%
- 27.8%
- 48%
- 94.66%
Solución:
Para encontrar la solución, debemos identificar lo que nos está ofreciendo el problema para responder a la pregunta. Las probabilidades de que cada máquina saque un producto defectuoso, corresponden al evento P\left(D \mid M_{i}\right) con D=\text { defectuoso y } M_{i} es una de las 3 máquinas.
Por otra parte, lo solicitado es la probabilidad de escoger una lata que cumpla con las especificaciones, es decir se nos pide la probabilidad total P(N) \text { donde } N no es defectuoso. Para calcularla, empleamos el teorema de la probabilidad total:
P(N)=P\left(M_{1}\right) P\left(N \mid M_{1}\right)+P\left(M_{2}\right) P\left(N \mid M_{2}\right)+P\left(M_{3}\right) P\left(N \mid M_{3}\right)
Como el problema no nos indica la probabilidad asociada a cada máquina, asumimos que las tres tienen la misma probabilidad, es decir
P\left(M_{1}\right)=P\left(M_{2}\right)=P\left(M_{3}\right)=\frac{1}{3}
Solo nos falta P\left(N \mid M_{i}\right) asociada a cada máquina, como ya tenemos el evento opuesto, es decir P\left(D \mid M_{i}\right) , calculando el complemento de este último obtenemos a P\left(N \mid M_{i}\right) .
P\left(N \mid M_{1}\right)=100 \%-5 \%=95 \%
P\left(N \mid M_{2}\right)=100 \%-8 \%=92 \%
P\left(N \mid M_{3}\right)=100 \%-3 \%=97 \%
Sustituimos en la fórmula:
P(N)=\frac{1}{3}(0.95+0.92+0.97)=0.94666
Expresado en porcentaje:
P(N)=94.66 \%
Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).
Reactivo 34
Una caja negra contiene una esfera blanca y tres guindas, otra caja gris contiene cuatro esferas blancas y cuatro esferas guindas. Se selecciona una caja al azar y se elige una esfera. Si la esfera resultante es guinda, calcular la probabilidad de que provenga de la caja negra.
- 1/4
- 3/8
- 3/5
- 3/4
Solución:
Para calcular la probabilidad de escoger una guinda de la caja negra, debemos identificar los eventos en juego y las relaciones entre ellos.
Primero, están los eventos de esfera guinda G y escoger la caja negra C N . Además, hay guindas tanto en la caja negra como en la caja gris, por lo que la probabilidad P(G) se expresa como:
P(G)=P(G \cap C N)+P(G \cap C G)
Tanto P(G \cap C N) \text { у } P(G \cap C G) se calculan de los datos dados por el problema. En la caja negra hay 4 esferas: 1 blanca y 3 guindas. En la caja gris hay 8 esferas: 4 blancas y 4 guindas. Además, la probabilidad de escoger cualquiera de las cajas es de 1/2. Por tanto:
P(G)=\left(\frac{1}{2}\right)\left(\frac{3}{4}\right)+\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)=\frac{5}{8}
La probabilidad de escoger una esfera guinda en el experimento es 5/8. La probabilidad de seleccionar la caja negra y que salga una esfera guinda se expresa como:
P(C N \mid G)=\frac{P(C N \cap G)}{P(G)}=\frac{\left(\frac{1}{2}\right)\left(\frac{3}{4}\right)}{\frac{5}{8}}=\frac{\frac{3}{8}}{\frac{5}{8}}=\frac{3}{5}
En conclusión, la probabilidad de extraer una esfera guinda habiendo seleccionado la caja negra es del 60%. Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 35
La probabilidad de que un niño tenga cáncer es de 3%. Se dispone de pruebas de diagnóstico médico, la probabilidad de que un resultado sea positivo, dado que tiene cáncer es 90% y positivo dado que no está presente la enfermedad es 2%. Suponga que la prueba de diagnóstico médico ha dado un resultado positivo.
¿Cuál es la probabilidad de que no esté presente la enfermedad?
- 0.3715
- 0.4181
- 0.5855
- 0.6025
Solución:
Antes de comenzar a escribir ecuaciones, es necesario identificar cada uno de los datos del problema y entender qué relación tiene con la situación que se plantea.
El ejercicio trata de unas pruebas diagnóstico para el cáncer en niños, el 3% de ellos padecen la enfermedad y la probabilidad de que las pruebas den positivo es 90% si el niño es paciente oncológico y un 2% de dar positivo cuando no lo es. Todos estos datos se expresan así:
\text { Probabilidad de que un niño tenga cáncer: } P(C)=3 \%=0.03
\text { Probabilidad de positivo si tiene cáncer: } P(P \mid C)=90 \%=0.9
\text { Probabilidad de positivo si no tiene cáncer: } P(P \mid N C)=2 \%=0.02
El problema pregunta por la probabilidad de que no tenga cáncer y de positivo P(N C \mid P) .
P(N C \mid P)=\frac{P(N C \cap P)}{P(P)}
P(P) se calcula con el teorema de la probabilidad total.
P(P)=P(P \cap N C)+P(P \cap C)
Además:
P(P \mid C)=\frac{P(P \cap C)}{P(C)} \rightarrow P(P \cap C)=P(P \mid C) P(C)
P(P \mid N C)=\frac{P(P \cap N C)}{P(N C)} \rightarrow P(P \cap N C)=P(P \mid N C) P(N C)
P(N C) es el complemento de P(C) .
P(N C)=100 \%-P(C)=100 \%-3 \%=97 \%
P(P \cap C)=P(P \mid C) P(C)=(0.9)(0.03)=0.027
P(P \cap N C)=P(P \mid N C) P(N C)=(0.02)(0.97)=0.0194
Calculamos entonces a P(P) .
P(P)=P(P \cap N C)+P(P \cap C)=0.027+0.0194=0.0464
Ya que P(P \cap N C)=P(N C \cap P)
P(N C \mid P)=\frac{P(N C \cap P)}{P(P)}=\frac{0.0194}{0.0464}=0.4181
Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).
Reactivo 36
El departamento de crédito de la tienda Elkar, informó que 30% de sus ventas son en efectivo y 70% a crédito. Tiene que el 20% de las compras en efectivo y 60% a crédito son por más de $500. Natalia compró un vestido que cuesta $1800 ¿Cuál es la probabilidad de que haya pagado en efectivo?
- 0.125
- 0.345
- 0.654
- 0.873
Solución:
Aplicando el teorema o regla de Bayes, podremos llegar a la respuesta con gran rapidez. El teorema enuncia lo siguiente:
P\left(B_{r} \mid A\right)=\frac{P\left(B_{r}\right) P\left(A \mid B_{r}\right)}{\sum_{i=1}^{k} P\left(B_{i}\right) P\left(A \mid B_{i}\right)}
Es decir, que la probabilidad condicional de un evento aleatorio B_{r} dado A se puede escribir en términos de la probabilidad condicional de A dado B_{r} y las probabilidades condicionales del resto de eventos B_{i} que desencadenan a A .
En nuestro caso, los eventos son:
V E: \text { ventas en efectivo. }
V C: \text { ventas a crédito. }
M Q: \text { compras por más de } \$ 500 .
Las probabilidades en relación con los eventos son:
P(V E)=30 \%=0.3
P(V C)=70 \%=0.7
P(M Q \mid V E)=20 \%=0.2
P(M Q \mid V C)=60 \%=0.6
Y se nos pide la probabilidad condicionada de que una Venta en Efectivo sea por Más de Quinientos. Según el teorema de Bayes esto quedaría como:
P(V E \mid M Q)=\frac{P(V E) P(M Q \mid V E)}{P(M Q \mid V E) P(V E)+P(M Q \mid V C) P(V C)}
Sustituyendo queda:
P(V E \mid M Q)=\frac{(0.3)(0.2)}{(0,2)(0.3)+(0.6)(0.7)}=\frac{0.06}{0.48}=0.125
Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).
Reactivo 37
El siguiente histograma muestra la distribución de las calificaciones finales de un grupo de estudiantes.
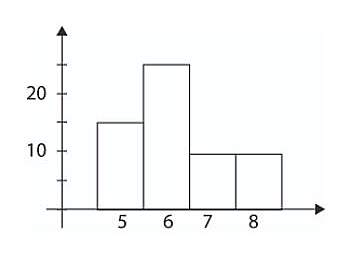
Calcular el porcentaje de estudiantes que aprobaron.
- 67.70%
- 71.38%
- 75.00%
- 78.00%
Solución:
Con ayuda del histograma, podemos crear la siguiente tabla de distribución:

Un estudiante se considera aprobado si su calificación es mayor o igual que 6. Según la tabla de datos hay: 25 estudiantes con 6, 10 estudiantes con 7 y 10 estudiantes con nota final igual a 8. Es decir, 45 estudiantes aprobados. Además, el total de estudiantes que cursaron la asignatura fue de 60.
El porcentaje de estudiantes aprobados se calcula como:
\% E A=\frac{N^{\circ} E A}{N^{\circ} T E} * 100 \%=\frac{45}{60} * 100 \%=75 \%
Con base en las opciones que ofrece el ejercicio, la respuesta correcta es la c).
Reactivo 38
Identificar en el siguiente histograma la barra que representa la frecuencia acumulada cuyo valor es de 34.
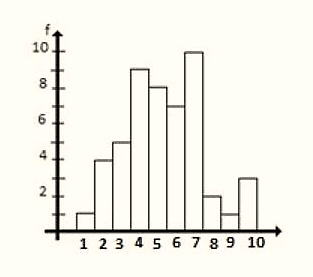
- 4
- 6
- 8
- 9
Solución:
La frecuencia acumulada F_{i} se calcula sumando la frecuencia absoluta o relativa de forma consecutiva a lo largo de los datos en un experimento aleatorio. Para visualizar mejor esto, construyamos la tabla con los datos mostrados en el histograma.
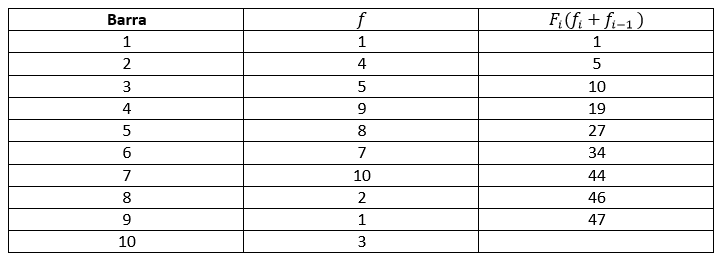
A partir de la tabla, podemos determinar que el dato o barra con frecuencia acumulada igual a 34 es 6. Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).
Reactivo 39
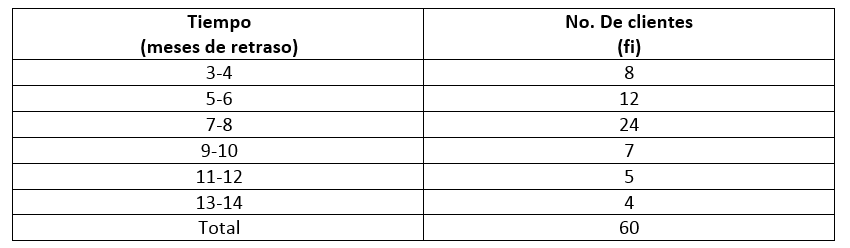
La siguiente tabla muestra la cantidad de meses de retraso de clientes morosos. Especificar el intervalo en el que se ubica la media.
- Primero
- Tercero
- Cuarto
- Sexto
Solución:
Por simple inspección en los datos, podemos intuir que la media debe encontrarse en el tercer intervalo de datos, ¿razón? Es el intervalo con mayor cantidad de población. Para comprobar nuestras sospechas, debemos calcular la media aritmética del conjunto de datos para compararla con los datos.
Para calcular la media aritmética de un conjunto de datos agrupados, se debe multiplicar la marca de clase por su frecuencia absoluta correspondiente y la suma de todos esos productos dividida entre el número total de eventos.
\bar{x}=\frac{\sum x_{i} f_{i}}{n}
Donde:
- x_{i} es la marca de una de las clases
- f_{i} es la frecuencia absoluta de una de las clases
- n es el total de observaciones o eventos
El problema nos da los intervalos o clases, pero no las marcas, es necesario calcularlas. La marca de clase se obtiene de la semisuma de los extremos del intervalo:
x_{i}=\frac{L_{\text {sup }}+L_{\text {inf }}}{2}
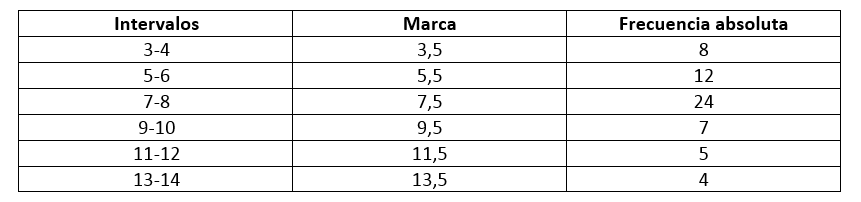
Con todos los datos y sabiendo que el total de observaciones es 60, procedemos a calcular la media de los meses de mora:
\bar{x}=\frac{(8)(3,5)+(12)(5,5)+(24)(7,5)+(7)(9,5)+(5)(11,5)+(4)(13,5)}{60}=7,533
Valor que efectivamente se ubica en el tercer intervalo 7-8. Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).
Reactivo 40
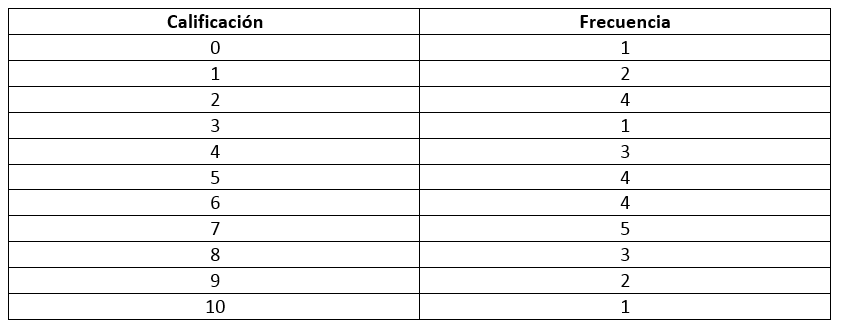
En la tabla se muestra la distribución de frecuencias de las calificaciones de 30 alumnos. Determinar la moda.
- 4
- 5
- 6
- 7
Solución:
En estadística, la moda es el valor que aparece con mayor frecuencia en un conjunto de datos respecto a un experimento aleatorio cualquiera. Si examinamos la tabla de datos del problema, encontraremos que la calificación de 7 puntos es la nota con mayor moda.
Por tanto, concluimos que la respuesta correcta es la opción d).


