Llegamos a la parte final de la solución del examen simulacro. ¿Lograste resolver los 50 reactivos por tu cuenta? En la parte 5, resolveremos los últimos 10 ejercicios de probabilidad y estadística.

Recuerda seguir practicando. Si tienes dudas, no olvides que en nuestro curso repasamos todos los temas y materias incluidos en el nuevo examen de admisión al IPN.
Reactivo 41
El gráfico muestra la distribución de edades de 50 visitantes a cierto museo de arte. ¿En qué barra se encuentra la mediana de las edades?
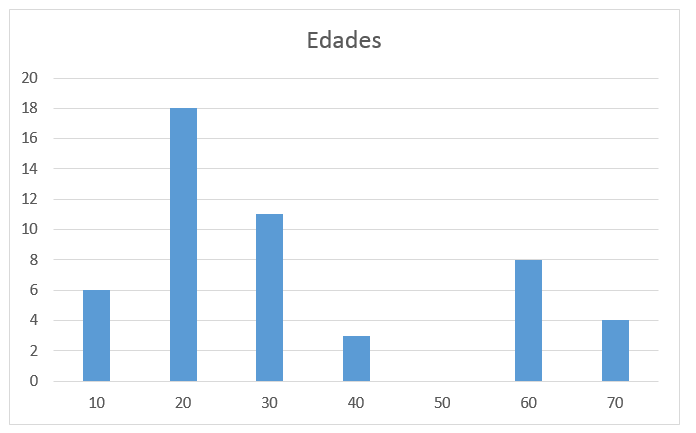
- Segunda
- Tercera
- Sexta
- Séptima
Solución:
La mediana es un valor de tendencia central que parte al conjunto de datos previamente ordenado en dos grupos con la misma cantidad de valores. Primero, se colocan los datos en una tabla y se determina la frecuencia acumulada para cada uno de ellos.
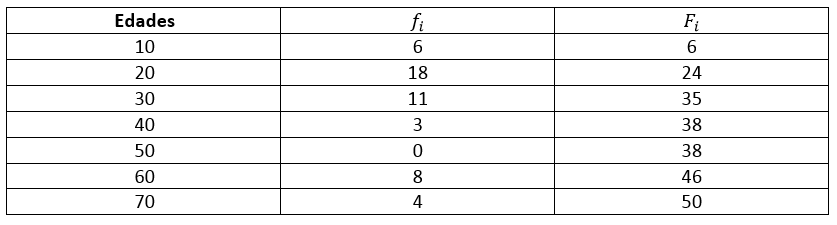
Ya los datos se encuentran ordenados de forma creciente. Como la cantidad de datos es par, 50 encontramos la posición de la mediana dividiendo entre 2.
P_{m e}=\frac{50}{2}=25
Ahora, se busca este resultado en la columna de frecuencias acumuladas, el dato que tenga una frecuencia acumulada inmediatamente mayor o igual al resultado obtenido, será la mediana.
Nuestro resultado es 25 y el inmediato superior es F_{i}=35 que corresponde a 30 años de edad o a la tercera columna. La respuesta correcta al problema es la opción b).
Reactivo 42
Ordenar los pasos en la construcción de una tabla de distribución de frecuencias para datos agrupados considerando el mismo ancho de clase.
- Conteo de los datos
- Calcular el ancho de la clase
- Determinar los límites de cada clase
- Especificar el número total de clases
- Acomodar los datos de menor a mayor
- 4, 2, 1, 5, 3
- 4, 3, 2, 1, 5
- 5, 4, 2, 3, 1
- 5, 4, 3, 2, 1
Solución:
Para construir correctamente una tabla de distribuciones, se necesitan seguir una serie de pasos para asegurar que los datos y los intervalos se establezcan de forma correcta. A continuación, se enumerarán los pasos en orden correcto.
- Acomodar los datos de menor a mayor
El orden creciente en el acomodo de los datos facilitará la determinación de ciertos valores de medida central, como también la construcción de un histograma de frecuencias.
- Especificar el número total de clases
Existen diferentes convenciones para determinar el número de clases.
- Si la cantidad de datos es menor que 200, el número de clases será igual a la raíz cuadrada del número de datos
- Si es superior a 200, el número de clases será la raíz cúbica del número total de datos
- Calcular el ancho de la clase
Primero, determina el rango de la muestra como:
R=D_{m a}-D_{m e}
Luego, el tamaño de las clases es el cociente entre el rango y el número de clases:
T_{c}=\frac{R}{N_{c}}
- Determinar los límites de cada clase
Se determina el límite inferior L_{i} y superior L_{s} de cada intervalo de clase. Se inicia por el menor de los datos, se le suma el ancho de la clase y ambos valores serán los extremos. Esto se hace de forma progresiva hasta completar el número de intervalos calculado.
I_{c}=\left[L_{i}, L_{i}+T_{c}\right)
- Conteo de los datos
Luego de agrupar los intervalos en una tabla, se crea una columna en la que se coloca la frecuencia absoluta de la clase o, el número de veces que un dato se encuentra en dicha clase.
Uniendo todo nos queda que:
5, 4, 2, 3, 1
Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 43
En un examen médico escolar se obtuvieron los siguientes datos:
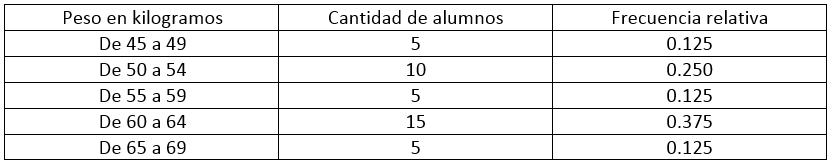
Calcular el límite real inferior de la clase modal.
- 59.0
- 59.5
- 60.0
- 64.5
Solución:
La moda es el valor que más se repite en un experimento estadístico. En conjuntos de datos agrupados, la clase modal es el intervalo de datos que posee la mayor frecuencia. En nuestro caso, el intervalo con la mayor frecuencia es De 60 a 64.
El límite real inferior se calcula como la media entre el límite superior de la clase antes de la modal y el límite inferior de la clase modal.
L M_{i}=\frac{59+60}{2}=59.5
Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).
Reactivo 44
Se grafica el ingreso per cápita (en miles) de la clase media en el área metropolitana para cierto año ¿Cuántas personas ganan el doble de un salario mínimo? Considerando el salario mínimo de $2400 mensuales.
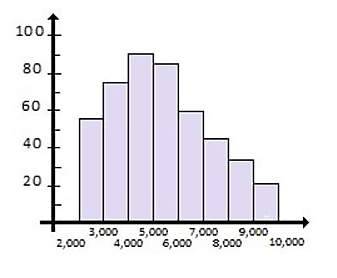
- 60
- 75
- 84
- 90
Solución:
Llevamos los datos recopilados en el histograma a una tabla de distribución de frecuencias.
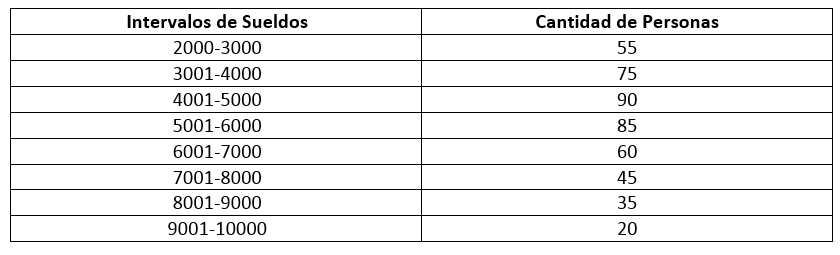
Si el salario mínimo es de $2400 el doble sería $4800, valor que se encuentra dentro del intervalo 4001-5000 en el que hay 90 personas. Por lo que concluimos que 90 personas en el área metropolitana en un cierto año ganaron el doble de un salario mínimo.
La respuesta correcta sería la opción d).
Reactivo 45
Sean los siguientes datos los minutos que 10 automóviles tardaron en recorrer 6 km en un día con tráfico moderado. Obtener la media y la moda.
\{14,15,12,18,17,14,19,16,15,20\}
- Mediana 16 – Moda 14
- Mediana 15.5 – Moda 14
- Mediana 14 – Moda 14 y 15
- Mediana 15.5 – Moda 14 y 15
Solución:
Primero, es necesario ordenar los datos de forma creciente.
\{12,14,14,15,15,16,17,18,19,20\}
La moda será el o los valores que más se repitan, en este caso son 14 y 15 que se repiten 2 veces cada uno. La mediana es el valor que divide a los datos a la mitad, como hay 10 datos la mediana es la media aritmética de los valores centrales 15 \text { y } 16 , por tanto:
M_{e}=\frac{15+16}{2}=15.5
Concluimos que la moda son 14 y 15 y la mediana es 15.5. Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).
Reactivo 46
La siguiente tabla muestra los registros de tiempo (en segundos) para el ensamble de una pieza automotriz ¿Cuál es la media y la mediana?
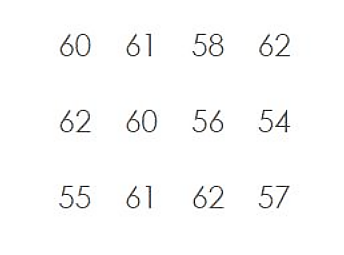
- \text { Media }=58, \text { Mediana }=59
- \text { Media }=59, \text { Mediana }=59
- \text { Media }=59, \text { Mediana }=60
- \text { Media }=60, \text { Mediana }=61
Solución:
Primero, procedemos a ordenar los datos de forma creciente.
54,55,56,57,58,60,60,61,61,62,62,62
La media de un conjunto de datos no agrupados es el promedio de los valores recolectados. Por tanto:
\bar{x}=\frac{54+55+56+57+58+60+60+61+61+62+62+62}{12}=59
Para la mediana, calculamos el promedio de los datos centrales por ser una población par.
M_{e}=\frac{60+60}{2}=60
Concluimos entonces que la mediana es 60 y la media es 59. Comparando con las opciones, la respuesta correcta es la c).
Reactivo 47
De un conjunto de 5 números se calcula la media; después, cada uno de los números incrementa en 10 unidades ¿Cómo es la nueva media comparada con la original?
- Es igual
- Aumentó en 2 unidades
- Aumentó en 10 unidades
- Aumentó en 50 unidades
Solución:
Esto será sencillo de demostrar. Recordemos la definición de media para datos no agrupados:
\bar{x}=\frac{\sum x_{i}}{n}
So el conjunto de datos es 5, la ecuación queda como:
\bar{x}_{1}=\frac{x_{1}+x_{2}+x_{3}+x_{4}+x_{5}}{5}
Sumemos a cada número 10, tal como lo indica el problema.
\bar{x}_{2}=\frac{x_{1}+10+x_{2}+10+x_{3}+10+x_{4}+10+x_{5}+10}{5}
Agrupamos a un lado los 10 y a otro los números.
\bar{x}_{2}=\frac{5(10)+\left(x_{1}+x_{2}+x_{3}+x_{4}+x_{5}\right)}{5}
Separamos y simplificamos.
\bar{x}_{2}=10+\bar{x}_{1}
Concluimos que la media originar aumenta en 10 unidades. Comparando con las opciones del problema, la respuesta correcta es la c).
Reactivo 48
La siguiente distribución muestra el tiempo de espera para la atención de clientes en un banco.

¿Cuál es el valor del tiempo medio de consulta?
- 2,52
- 6,03
- 8,57
- 17,51
Solución:
Para calcular la media aritmética de un conjunto de datos agrupados, es decir datos establecidos por intervalos, se debe multiplicar la marca de clase por su frecuencia absoluta correspondiente y la suma de todos esos productos dividida entre el número total de eventos.
\bar{x}=\frac{\sum x_{i} f_{i}}{n}
Donde:
- x_{i} es la marca de una de las clases
- f_{i} es la frecuencia absoluta de una de las clases
- n es el total de observaciones o eventos
El problema nos da los intervalos o clases, pero no las marcas, es necesario calcularlas. La marca de clase se obtiene de la semisuma de los extremos del intervalo:
x_{i}=\frac{L_{\text {sup }}+L_{\text {inf }}}{2}
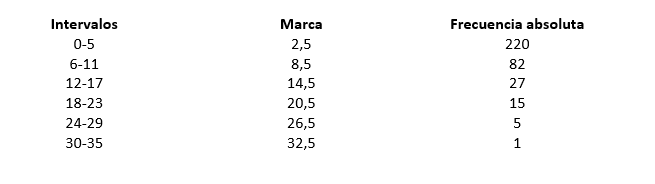
Con todos los datos y sabiendo que el total de observaciones es 350, procedemos a calcular la media del tiempo de consulta:
\bar{x}=\frac{(220)(2,5)+(82)(8,5)+(27)(14,5)+(15)(20,5)+(5)(26,5)+(1)(32,5)}{350}=\frac{2111}{350}
\bar{x}=6,03 \mathrm{~min}
Concluimos entonces que el tiempo medio de espera es de 6,03 minutos. Según las opciones del problema, seleccionamos como correcta a la b).
Reactivo 49
El siguiente polígono de frecuencias indica el número de personas que obtuvieron entre 80 y 120 aciertos en el examen de admisión al IPN.
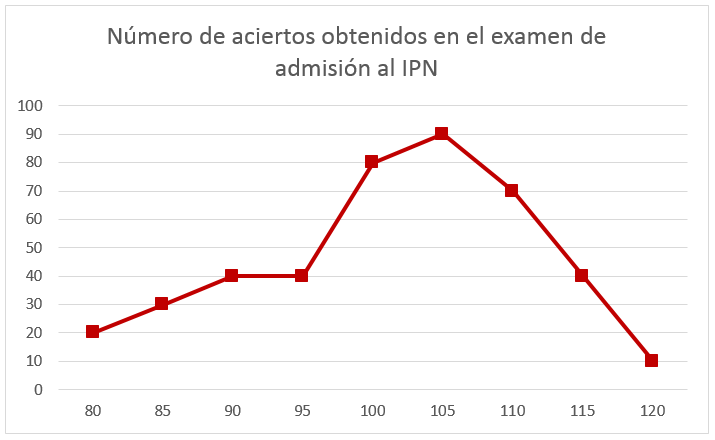
Obtener la mediana de la muestra.
- 100 aciertos
- 105 aciertos
- 104 aciertos
- 102 aciertos
Solución:
Como en todos los problemas de estadística, pasemos los datos a una tabla de frecuencias para trabajar con mayor comodidad.
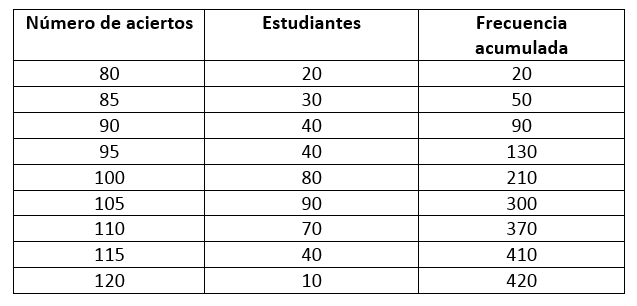
Como la cantidad de datos es par, 420 encontramos la posición de la mediana dividiendo entre 2.
P_{m e}=\frac{420}{2}=210
Ahora, se busca este resultado en la columna de frecuencias acumuladas, el dato que tenga una frecuencia acumulada inmediatamente mayor o igual al resultado obtenido, será la mediana.
Nuestro resultado es 210 igual a la frecuencia acumulada de 100 aciertos. La respuesta correcta al problema es la opción a).
Reactivo 50
Un conjunto de diez datos tiene media 6, otro conjunto de treinta datos tiene media 10, ambos conjuntos se juntan como uno solo. Calcular la media del nuevo conjunto.
- 8.0
- 8.5
- 9.0
- 9.5
Solución:
En este caso, se pide calcular la media luego de unir ambos conjuntos de datos. A la media del primer conjunto de datos la llamamos \bar{x}_{1}=6 y al total de sus datos n_{1}=10 . Por otra parte, al segundo conjunto \bar{x}_{2}=10 y al total de sus datos n_{2}=30 .
De la fórmula para calcular la media de datos no agrupados tenemos que:
\bar{x}=\frac{\sum x_{i}}{n} \rightarrow \sum x_{i}=n \bar{x}
En ambos conjuntos de datos obtenemos:
\sum x_{i}=n_{1} \bar{x}_{1}
\sum x_{j}=n_{2} \bar{x}_{2}
El nuevo conjunto de datos tiene como datos a \sum x_{i_{1}}+\sum x_{j_{2}} y de número total n_{2}+n_{1} . Por tanto, la media del nuevo conjunto es:
\bar{x}_{1,2}=\frac{\sum x_{i_{1}}+\sum x_{j_{2}}}{n_{2}+n_{1}}=\frac{n_{1} \bar{x}_{1}+n_{2} \bar{x}_{2}}{n_{2}+n_{1}}
Sustituimos en la ecuación.
\bar{x}_{1,2}=\frac{(10)(6)+(30)(10)}{40}=9
Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).


