Probabilidad y estadística es uno de los temas fundamentales de matemáticas en el nuevo examen de admisión al IPN. Con este examen simulacro podrás poner a prueba tus conocimientos con 50 reactivos de este tema.

¿Por qué debes realizar exámenes simulacro? Son la mejor herramienta al momento de poner a prueba tus conocimientos, y sobre todo, mejorar tu tiempo de respuesta.
Recuerda que el examen tiene un tiempo límite para responder los 140 reactivos.
Estructura del examen IPN
El examen de admisión del IPN se compone de 8 materias. Para cada área la cantidad de reactivos varía dependiendo del área del conocimiento, aunque independientemente de la carrera a la que apliques en tu examen deberás responder 140 reactivos.
A continuación puedes conocer la estructura del examen, y distribución de reactivos por materia.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
Temario de probabilidad y estadística
Matemáticas se compone de 7 temas, siendo el de probabilidad y estadística uno de ellos.
Estos son los temas correspondientes a esta materia:
- Probabilidad
- Teoría de conjuntos
- Técnicas de conteo
- Espacios muestrales
- Probabilidad de un evento
- Eventos aleatorios
- Probabilidad condicional
- Eventos dependientes e independientes
- Teorema de Bayes
- Estadística descriptiva
- Tablas de distribución de frecuencias
- Gráficas de datos
- Muestra y población
- Medidas de tendencia central
- Medidas de posición
- Medidas de dispersión
Ejercicios examen simulacro
Hemos dividido los 50 ejercicios de probabilidad y estadísticas en 5 partes, estos ejercicios tienen la finalidad de que identifiques si tienes el conocimiento necesario para obtener un buen puntaje en esta materia.
Reactivo 1
Por definición, ______________ se forma por todos los elementos dentro de un conjunto universo U que no son elementos del conjunto A .
- El complemento
- La intersección
- La diferencia
- La unión
Solución:
Según la Teoría de Conjuntos, el complemento de un conjunto A es el conjunto A^{c} que contiene a todos los elementos que no pertenecen a A , respecto de un conjunto universo. Esto podemos representarlo mediante un diagrama de Venn.
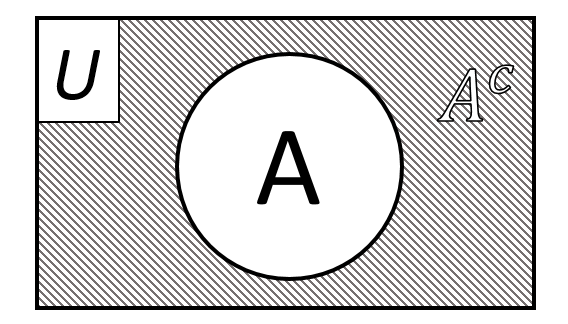
Con base en la definición anterior y apoyados en el diagrama, la respuesta correcta es la opción a). La frase completa sería:
Por definición, el complemento se forma por todos los elementos dentro de un conjunto universo U que no son elementos del conjunto A .
Reactivo 2
El enunciado “ x pertenece al conjunto Q pero no al conjunto P ” es una forma de representar la:
- Complementación
- Intersección
- Diferencia
- Unión
Solución:
Al igual que con los números podemos realizar las típicas operaciones de suma, resta, multiplicación y división, entre conjunto también se establecen ciertas operaciones. En el enunciado del problema, se está indicando que un elemento x pertenece a Q pero no a P .
Dicha comparación, establece una diferencia entre ambos conjuntos, donde x es un elemento que posee el conjunto Q pero no el conjunto P . En base a este sencillo análisis, concluimos que la respuesta correcta es la opción c).
Reactivo 3
Siendo A, B, C conjuntos no vacíos, relacionar las siguientes expresiones con su respectiva propiedad.
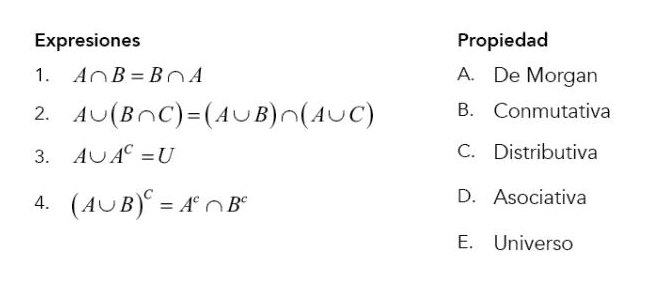
- 1B, 2E, 3C, 4A
- 1B, 2C, 3E, 4A
- 1E, 2D, 3A, 4C
- 1E, 2D, 3B, 4C
Solución:
Para encontrar la respuesta correcta, analizaremos cada una de las expresiones en la columna izquierda para luego relacionarlas con una de las propiedades en la columna derecha.
- A \cap B=B \cap A
Esta primera expresión indica que la intersección de A con B es igual a la intersección de B con A . Es decir, no importa el orden de los operandos, la intersección entre dos conjuntos es siempre el mismo resultado.
Eso último no es más que la propiedad conmutativa respecto a la operación intersección, por tanto: 1B.
- A \cup(B \cap C)=(A \cup B) \cap(A \cup C)
La igualdad establece que: la unión de A con la intersección de B con C es igual a la intersección de las uniones de A con B y A con C .
La descripción anterior concuerda con la propiedad distributiva respecto a la intersección y unión de conjuntos, por tanto: 2C.
- A \cup A^{C}=U
La definición del complemento de un conjunto dice que es el conjunto con todos los elementos que no pertenecen a A respecto de un conjunto universo U . Es decir, si unimos a A con su complemento, obtenemos al conjunto universo, por tanto: 3E.
- (A \cup B)^{C}=A^{c} \cap B^{c}
Esta última expresión es especial ya que es una de las Leyes de D Morgan. Ambas reglas permiten transformar expresiones escritas en disyunción a conjunción y viceversa, aplicando la negación o el complemento sobre ellas. En base a esto, concluimos que: 4A.
Uniendo la respuesta dada para cada inciso tenemos que:
1B, 2C, 3E, 4A
Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).
Reactivo 4
Expresar el conjunto P=\{2,3,4,5,6,9,16,25,36\} en términos de R=\{4,9,16,25,36\} \text { y } S=\{2,3,4,5,6\} .
- R-S
- S^{C} \cup R
- R \cup \mathrm{S}
- S \cap R
Solución:
Para resolver este problema, solo debemos identificar la operación entre los conjuntos R \text { y } S que dé como resultado al conjunto P . Lo primero que podemos ver, es que tanto R como S son subconjuntos de P , es decir:
R \subset P \text { y } S \subset P
Si realizamos la unión entre ambos conjuntos obtenemos:
R \cup S=\{4,9,16,25,36\} \cup\{2,3,4,5,6\}=\{2,3,4,5,6,9,16,25,36\}
Resultado que es igual al conjunto P . Concluimos entonces que:
R \cup S=P
Comparando con las opciones que ofrece el problema, la respuesta correcta sería la c).
Reactivo 5
Determinar (A \cap B \cap C) \text { si } A=\{1,2,3,4\}, B=\{2,4,6,8\} \text { y } C=\{1,3,5,7\}
- \{1\}
- \{2\}
- \{\emptyset\}
- \{1,2\}
Solución:
La operación que solicita el problema, es la de interceptar a los tres conjuntos A, B, C . Es decir, debemos determinar los elementos que son comunes en los tres conjuntos. Para ello, nos apoyaremos en la propiedad asociativa respecto de la intersección.
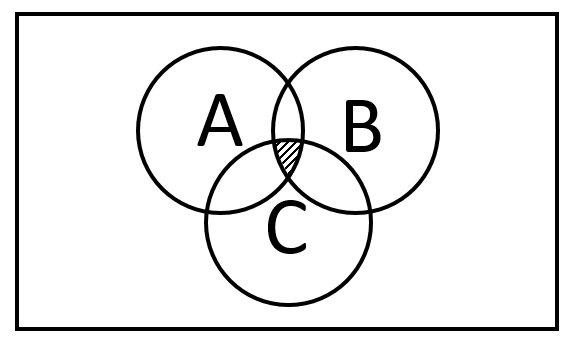
Primero calcularemos la intersección entre B \text { у } C y ese resultado lo interceptaremos con A .
A \cap B \cap C=A \cap(B \cap C)
Calculamos la intersección entre B \text { у } C :
B \cap C=\{2,4,6,8\} \cap\{1,3,5,7\}
Como no existen elementos comunes entre B \text { у } C , su intersección es el conjunto vacío.
B \cap C=\{2,4,6,8\} \cap\{1,3,5,7\}=\{\emptyset\}
En consecuencia, la intersección de A con el conjunto vacío es también el conjunto vacío.
A \cap(B \cap C)=\{1,2,3,4\} \cap\{\emptyset\}=\{\emptyset\}
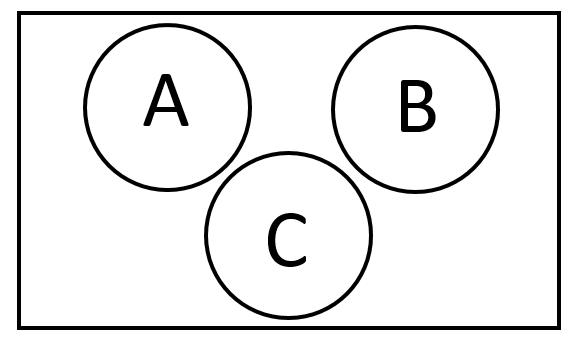
Concluimos entonces que A \cap B \cap C es igual al conjunto vacío \{\emptyset\} . Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 6
Dados los siguientes conjuntos A=\{1,2,4,5\}, B=\{2,4,6,7\}, U=\{1,2,3,4,5,6,7,8\} encontrar el evento \left(\mathrm{A}^{C} \cap \mathrm{B}^{C}\right) .
- \{3,4\}
- \{5,6\}
- \{3,6\}
- \{3,8\}
Solución:
En este caso, el ejercicio nos provee tres conjuntos, donde uno de ellos es el conjunto universo al que pertenecen los otros dos.
La operación que se nos pide calcular es la intersección de los complementos de ambos conjuntos. Por lo que, determinamos sus complementos y luego intersectamos dichos resultados. El complemento de un conjunto es igual a su diferencia con el conjunto universal.
A^{c}=U-A
Complemento del conjunto A .
A^{c}=\{1,2,3,4,5,6,7,8\}-\{1,2,4,5\}=\{3,6,7,8\}
Complemento del conjunto B .
B^{c}=\{1,2,3,4,5,6,7,8\}-\{2,4,6,7\}=\{1,3,5,8\}
Ahora, solo nos queda intersectar ambos resultados.
A^{C} \cap B^{C}=\{3,6,7,8\} \cap\{1,3,5,8\}=\{3,8\}
La intersección de los complementos de A \text { y } B \text { es }\{3,8\} . Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).
Reactivo 7
Escribir mediante lenguaje de conjuntos la expresión que describe la región sombreada del siguiente diagrama de Venn:
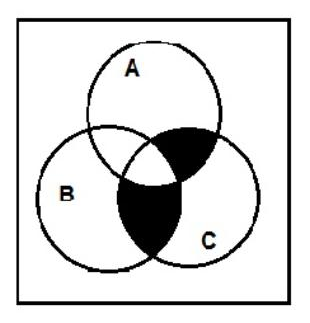
- [(A \cap B) \cup(B \cap C)]-(A \cap C)
- [(A \cap C) \cup(B \cap C)]-(A \cap B)
- [(A \cap B) \cap(B \cap C)]-(A \cap B)
- [(A \cap C) \cap(B \cap C)]-(A \cap C)
Solución:
Aunque parezca complejo, lo primero que debemos hacer es identificar a qué uniones o intersecciones corresponde cada sección sombreada, unirlas y por último restar las regiones que no deberían estar sombreadas.
Haciendo una inspección rápida, nos daremos cuenta de que la intersección entre el conjunto B y el conjunto C corresponde a la sección sombreada inferior; y la intersección entre A \text { у } C corresponde a la sección sombreada a la derecha.
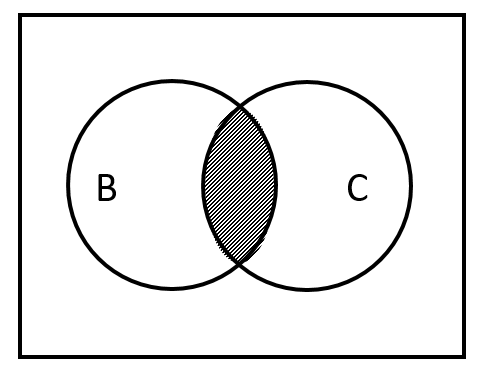
B \cap C
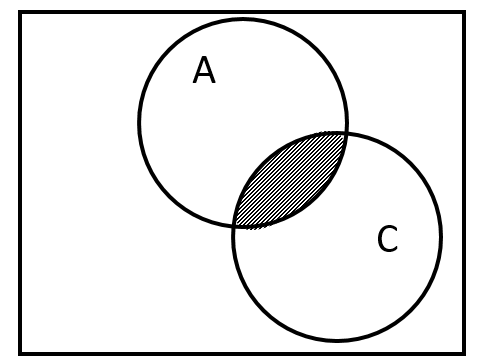
A \cap C
Si unimos ambas intersecciones, obtenemos a la región sombreada sin eliminar las zonas no correspondientes.
(A \cap C) \cup(B \cap C)
La zona que no debería estar sombreada, podemos extraerla de la intersección entre el conjunto B y el conjunto A , para luego restarla al conjunto deducido anteriormente.
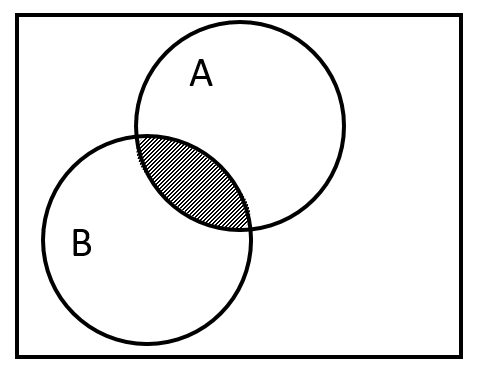
A \cap B
Recordemos lo que enuncia la diferencia de conjuntos:
La diferencia de dos conjuntos A \text { y } B es el conjunto de elementos que pertenecen a A , pero no a A .
Es decir, al restar A \cap B del conjunto solución anterior obtendremos la región sombreada que solicita el problema. Por tanto:
[(A \cap C) \cup(B \cap C)]-(A \cap B)
Es el diagrama de Venn escrito en lenguaje de conjuntos. Comparando con las opciones que ofrece el enunciado, escogemos a b) como la respuesta correcta.
Reactivo 8
De acuerdo al siguiente diagrama de Venn. Determinar la siguiente operación de conjuntos: (A \cup B \cup C)^{C}
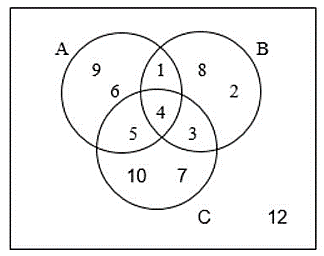
- \{4\}
- \{4\}
- \{12\}
- \{1,3,5\}
Solución:
Para resolver este problema, existen diferentes vías. Podríamos aplicar una de las Leyes de De Morgan para convertir la expresión en términos de uniones a intersecciones, analizar cada conjunto por separado o extraer información general a partir del diagrama de Venn.
Por ser el camino más rápido, optamos por analizar de forma general el diagrama de Venn. La expresión dentro de los paréntesis (sin tomar en cuenta al complemento) es la unión de los tres conjuntos.
A \cup B \cup C=\{1,2,3,4,5,6,7,8,9,10\}
Además, estos conjuntos se encuentran dentro de un conjunto Universo cuyos elementos son:
U=\{1,2,3,4,5,6,7,8,9,10,12\}
Entonces, podemos determinar el complemento de la unión de A, B, C como:
(A \cup B \cup C)^{C}=U-(A \cup B \cup C)
=\{1,2,3,4,5,6,7,8,9,10,12\}-\{1,2,3,4,5,6,7,8,9,10\}=\{12\}
Comparando este resultado con las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 9
Relacionar el diagrama de Venn con la expresión de conjuntos que le corresponda.
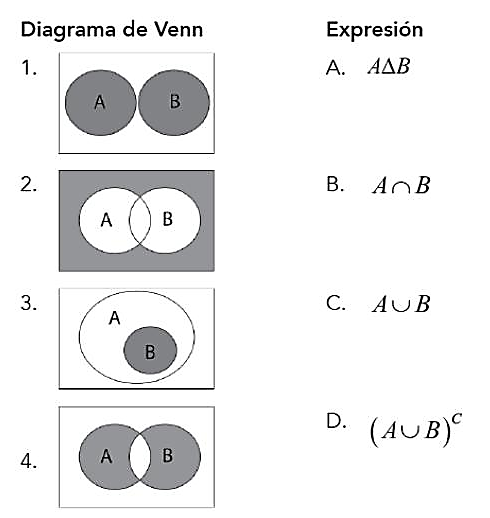
- 1C, 2A, 3B, 4D
- 1A, 2C, 2B, 4D
- 1A, 2D, 3C, 4B
- 1C, 2D, 3B, 4A
Solución:
Para dar con la solución a este problema, analizaremos cada uno de los diagramas en la columna izquierda y relacionarlo con una de las expresiones en la columna derecha.
Diagrama 1.
En este primer diagrama se ven dos conjuntos, A \text { у } B que se encuentran sombreados, es decir, a todos los elementos dentro de A y dentro de B , dicha representación corresponde a la Unión de conjuntos, por tanto:
A \cup B
Concluimos que 1C.
Diagrama 2.
En el segundo diagrama, se encuentran sombreados todos los elementos que no pertenecen ni a A ni a B . Es decir, unidos los elementos de ambos conjuntos nos quedamos con los que se encuentran fuera de esa unión. Esto se representa como:
(A \cup B)^{C}
Concluimos que 2D.
Diagrama 3.
Acá, B es subconjunto de A es decir, se encuentra dentro de él. Esto podemos representarlo mediante la intersección entre A \text { у } B , ya que todos los elementos de B pertenecen a A la intersección tienen como resultado a B . Por tanto:
A \cap B
Concluimos que 3B.
Diagrama 4.
Este último diagrama simboliza a todos los elementos que no son comunes entre A \text { у } B , se conoce como diferencia simétrica y se simboliza como:
A \Delta B
Concluimos que 4A.
Uniendo todas las soluciones obtenemos:
1C, 2D, 3B, 4A
Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).
Reactivo 10
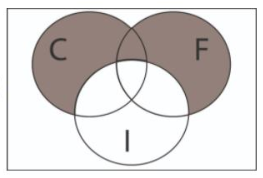
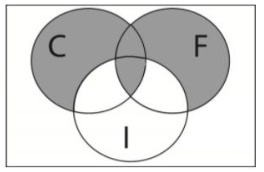
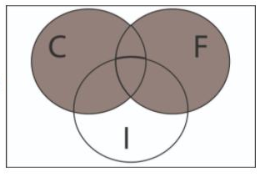
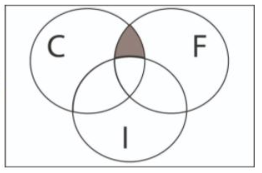
En una fiesta hay 3 sabores de pastel: chocolate (C), fresa (F) e imposible (I). Representar con un diagrama de Venn el evento: prefieren comer chocolate o de fresa, pero no el imposible.
Solución:
Para dar con el diagrama de Venn que representa al enunciado, es necesario analizar cada una de las relaciones que se establecen en él.
La parte del enunciado que dice: prefieren comer chocolate o de fresa… establece una disyunción entre el pastel de chocolate y el de fresa, en teoría de conjuntos esto lo entendemos como la unión entre el conjunto C y el conjunto F.
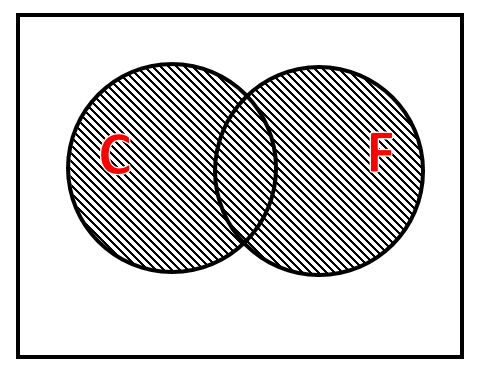
C \cup F
Al incluir el conjunto I en el problema con la otra parte de la frase: … Pero no el imposible, el diagrama de Venn se modifica, quedando:
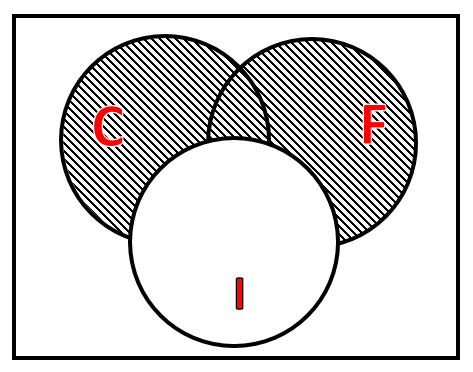
Comparando con las opciones que ofrece el problema, la respuesta correcta sería la a).