Examen Simulador IPN: Probabilidad y Estadística del 11 al 20

Segunda parte del examen simulacro de probabilidad y estadística para el examen de admisión al IPN. Vamos a resolver los reactivos del 11 al 20.

Antes de consultar el procedimiento, recuerda intentar resolver los ejercicios por tu cuenta.

Reactivo 11

Las __________ se emplean para describir el número de formas posibles de seleccionar r objetos de un total de n sin importar el orden.

1. Relaciones
2. Particiones
3. Permutaciones
4. Combinaciones

Solución:

En este problema, se nos pide completar el enunciado con el término correcto. De los temas referentes a la Probabilidad, sabemos que el número de formas que hay para seleccionar un número r de objetos, a partir de un total n se conoce como combinaciones y se calcula como:

C_{n}^{r}=\frac{n !}{r !(n-r) !} \text { para } n \geq r

Por ejemplo, si queremos saber cuántas combinaciones en parejas hay en un grupo de 10 personas, sustituimos a r=2 \text { у } n=10 en la ecuación.

C_{10}^{2}=\frac{10 !}{2 !(10-2) !}=45

Es decir, existen 45 formas de combinar en parejas a un grupo de 10 personas. Concluimos entonces que la opción correcta es la d) Combinaciones. La frase completada quedaría:

Las combinaciones se emplean para describir el número de formas posibles de seleccionar   r objetos de un total de n sin importar el orden.

Reactivo 12

Considere los conjuntos U=\{a, b, c, \ldots, z\} \text { Universo; } L=\{a, e, i, o, u\} y M=\{\text { números primos } \leq 11\} . Relacionar de manera correcta las columnas.

1. 1A, 2B, 3D, 4C, 5E
2. 1A, 2C, 3E, 4B, 5D
3. 1C, 2D, 3B, 4E, 5A
4. 1D, 2A, 3B, 4C, 5E

Solución:

Para encontrar la respuesta correcta, analizaremos cada una de las expresiones en la columna izquierda para relacionarla con un resultado en la columna derecha. Comenzamos por representar a los tres conjuntos mediante un diagrama de Venn.

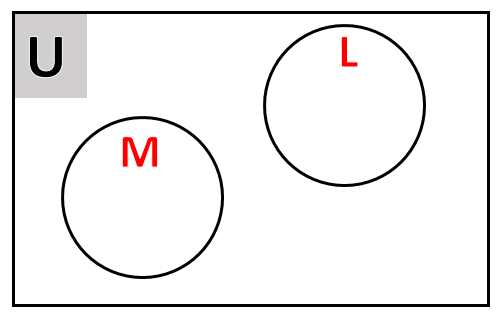
Además, notemos que L es subconjunto de U porque este último está compuesto por todas las letras del abecedario. Por otra parte, los elementos de M son:

M=\{1,2,3,5,7,11\}

Operación 1.

Esta primera operación corresponde a la unión de los conjuntos L \text { у } M

L \cup M=\{a, e, i, 0, u\} \cup\{1,2,3,5,7,11\}=\{a, e, i, 0, u, 1,2,3,5,7,11\}

Comparando con los incisos de la columna derecha, concluimos que: 1C.

Operación 2.

Recordemos que la diferencia entre el conjunto universo y cualquier otro conjunto es siempre igual al complemento de dicho conjunto, por tanto:

U-L=L^{c}

Comparando con los incisos de la columna derecha, concluimos que: 2D.

Operación 3.

Aunque el conjunto M este compuesto solo de números, el enunciado nos ha impuesto que U es el conjunto universo en este caso, por tanto:

M^{c}=U-M

Esta expresión no se encuentra en ninguno de los incisos, veamos cómo podemos simplificar. Recordemos que L es subconjunto de U y que ningún elemento de M está en U , por lo que el resto de elementos que no pertenecen a M son elementos de U , entonces:

M^{c}=U

Comparando con los incisos de la columna derecha, concluimos que: 3B.

Operación 4.

Tenemos varias formas de representar al conjunto universo, pero la que se encuentra presente entre las opciones es:

U=U \cup L

Recordemos que L \subset U , por lo que su unión es U . Comparando con los incisos de la columna derecha, concluimos que: 4E.

Operación 5.

La intersección de estos dos conjuntos es vacía, ya que U \text { y } M no tienen ningún elemento en común, por tanto:

U \cap M=\emptyset

Comparando con los incisos de la columna derecha, concluimos que: 5A.

Uniendo todas las respuestas obtenemos:

1C, 2D, 3B, 4E, 5A

Comparando con las opciones del problema, la respuesta correcta es la c).

Reactivo 13

El candado de un archivero tiene tres discos, cada uno de los cuales incluye los números enteros del 0 al 5. El candado se abre cuando la secuencia de los tres dígitos es correcta. Una persona olvida su clave, pero recuerda que ningún dígito se repite, calcular las secuencias de tres dígitos que puede probar para retirar el candado.

1. 60
2. 120
3. 125
4. 216

Solución:

Para resolver este problema, analizaremos las posibles ordenaciones que se tienen con los tres discos en el candado. Ya que los números son del 0 al 5, cada disco posee los mismos 6 dígitos.

D=\{0,1,2,3,4,5\}

Lo que necesitamos determinar son las permutaciones de estos 6 números en ternas, es decir en grupos de 3 no repetidos. Para ello, empleamos la fórmula de permutación:

{ }_{n} P_{r}=\frac{n !}{(n-r) !}

Siendo n=6 el conjunto total de objetos y r=3 la cantidad de objetos tomados a la vez.

{ }_{6} P_{3}=\frac{6 !}{(6-3) !}=120

Por tanto, existen 120 secuencias de 3 dígitos en el candado sin repetir ninguno, que debe probar la persona para retirar el candado. Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).

Reactivo 14

Calcular el número de cifras con tres dígitos que se pueden formar con los numerales 2, 3, 4 y 5 si se permite la repetición.

1. 4
2. 12
3. 16
4. 64

Solución:

En este caso, el conjunto de cifras es igual a 4 y se nos permite repetir. Es decir, que para el primer dígito podemos escoger entre los 4 numerales, para el siguiente también 4 y para el último 4 nuevamente.

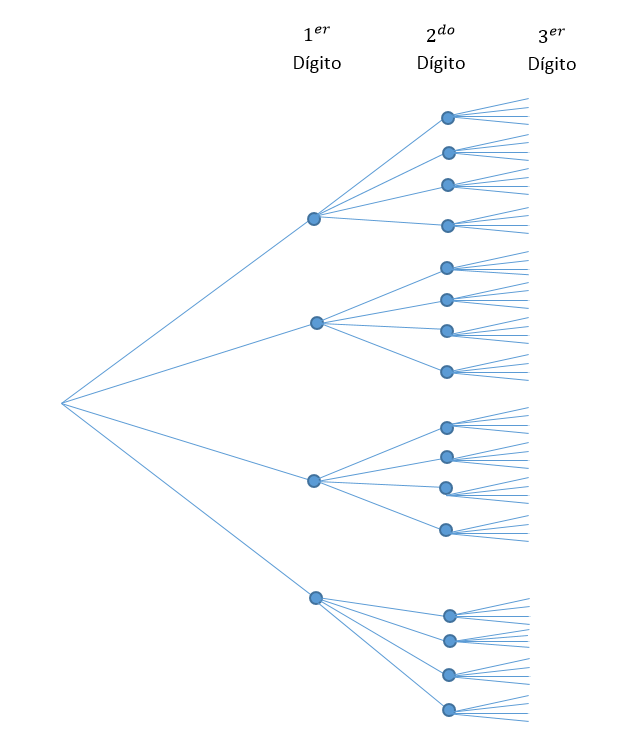
Con este diagrama de árbol, queda claro que el número de cifras con tres dígitos es:

N^{\circ} \text { de cifras }=4 \times 4 \times 4=64

Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 15

En una fiesta, todos los asistentes se saludaron entre sí. Hubo un total de 28 saludos ¿Cuántas personas asistieron a la fiesta?

1. 7
2. 8
3. 14
4. 28

Solución:

Para encontrar la respuesta correcta, analizaremos el problema desde una perspectiva más general. Imaginemos que el número de personas en la fiesta son vértices y que los saludos son conexiones entre esos puntos.

Además, no se permiten saludos dobles entre personas y tampoco importa el orden de saludo, es decir, no importa si es de A \text { a } B o de B \text { hacia } A , lo importante es que ocurra en cualquiera de las direcciones. Para el caso de 3, 4 y 5 personas, el diagrama de saludos sería:

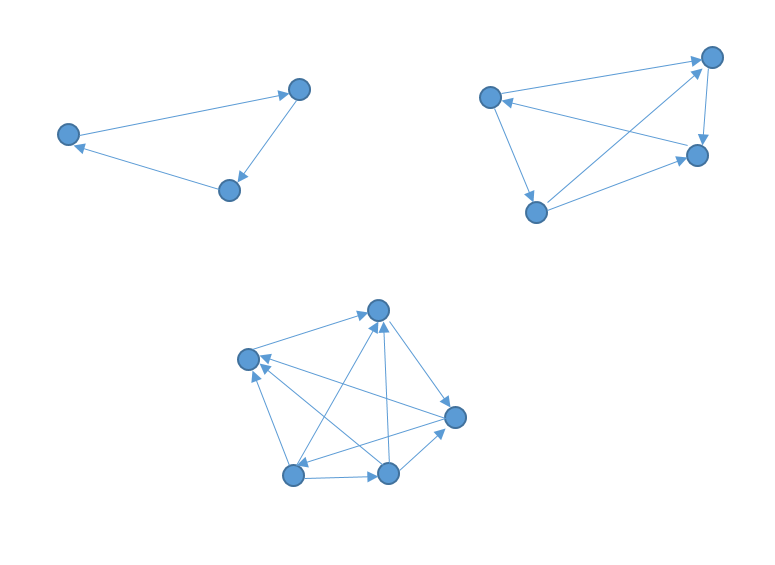
Las conexiones son los saludos entre las personas de cada grupo y las flechas indican la dirección del saludo. Es irrelevante el sentido, solo es necesario que se haga de una forma.

A partir del diagrama nos damos cuenta de que, por cada persona p se dan p-1 saludos (ya que nadie se saluda a sí mismo) y esto se repite por todas las p personas. Para eliminar las duplicidades, es necesario dividir entre dos quedando la expresión como:

N^{\circ} \text { saludos }=\frac{p(p-1)}{2}

Ya que el enunciado nos da el número de saludos totales, podemos despejar el número de personas.

\frac{p(p-1)}{2}=28 \rightarrow p^{2}-p-56=0

Aplicando la fórmula de la resolvente de segundo grado.

p=8

Concluimos entonces que la cantidad de personas en la fiesta es 8. Comparando con las opciones, la respuesta correcta es la b).

Reactivo 16

¿De cuántas formas diferentes se pueden sentar en la misma fila de un teatro, 7 amigos, si 4 son mujeres y 3 son hombres, y además quieren estar alternados?

1. 1
2. 28
3. 43
4. 144

Solución:

Tengamos en cuenta que para cualquiera que fuera la combinación, es necesario empezar siempre por una mujer, ya que si se comienza por un hombre no acabarán alternados.

A=\left\{m_{1}, h_{1}, m_{2}, h_{2}, m_{3}, h_{3}, m_{4}\right\}

Por otra parte, sabemos que por cada permutación en el orden de las mujeres, se presentan todas las permutaciones en el orden de los hombres (esto es recíproco).

Es decir, se dejan estáticas a las mujeres y se van cambiando a los hombres de lugar, cuando se han acabado todas las opciones, se cambia de lugar a una de las mujeres y comienza el conteo con los hombres nuevamente.

Aplicando la regla del producto, el total de las formas en que se pueden sentar es igual al producto de las permutaciones de los hombres con el de las mujeres:

P_{t}=P_{h} \times P_{m}=(3 !) \times(4 !)=144

Comparando con las opciones del problema, la respuesta correcta es la d).

Reactivo 17

Determinar cuántos números de 6 cifras se pueden construir con los dígitos 1, 2, 3, 5, 7, 9 sin repetir ningún dígito.

1. 720
2. 600
3. 120
4. 36

Solución:

Tengamos presente que, independientemente de los dígitos que nos da el enunciado, la cantidad de los mismos es 6. Cada vez que se coloca un número, disminuye en 1 la cantidad de dígitos para colocar la siguiente cifra.

Al principio tenemos 6, luego 5, después 4, así hasta que solo queda 1. Esto puede representarse a partir del factorial de la cantidad de cifras. Por tanto:

N^{\circ} \text { de disposiciones }=6 !=720

Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).

Reactivo 18

Una caja contiene 42 discos de vinil clásicos de Rock, se van a utilizar códigos de tres colores en cada uno, pero una combinación no puede ordenarse y utilizarse en otro disco, si se seleccionan 8 colores ¿Cuántos códigos cromáticos diferentes obtendrían?

1. 56
2. 64
3. 68
4. 96

Solución:

Para calcular la cantidad de códigos cromáticos diferentes, utilizaremos la fórmula de combinación.

C(n, r)=\frac{n !}{r !(n-r) !}

En nuestro caso, n es el total de colores, es decir, 8 y r es la cantidad de colores que se van a combinar a la vez, es decir 3. Sustituimos ambos valores en la fórmula.

C(8,3)=\frac{8 !}{3 !(8-3) !}=56

Por tanto, existen 56 formas de combinar a los 8 colores en ternas para crear los códigos cromáticos sin que sean reordenados. Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).

Reactivo 19

Juan, Sofía, Raquel, Fernando y Manuel se sientan en una mesa redonda de una cafetería, si Miguel es novio de Sofía, calcular el número de maneras diferentes en que se pueden sentar de tal manera que siempre estén juntos Manuel y Sofía.

1. 120
2. 24
3. 12
4. 6

Solución:

Para resolver este problema, es necesario recurrir a las permutaciones circulares. Como su nombre lo indica, son aquellas que se presentan al ordenar objetos en torno a una circunferencia. Este caso es especial, porque son dos los elementos que se mantienen fijos: Manuel y Sofía.

P_{c}=(n-2) !

¡Además, ellos también pueden permutarse de lugar 2 ! , por lo tanto, el número de formas diferentes en que pueden sentarse es:

P=(n-2) ! \times 2 !=(5-2) ! \times 2=12

Existen 12 formas en las que se pueden sentar para que Miguel y Sofía estén juntos. Comparando con las opciones del problema, la respuesta correcta es la c).

Reactivo 20

Encontrar los elementos del siguiente espacio muestral:

El conjunto de los números enteros entre 1 y 180, divisibles entre 15

1. \{15,45,60,90,105,120,135,150,165,180\}
2. \{15,30,45,60,75,90,105,120,135,150,165,180\}
3. \{1,15,25,45,60,75,85,105,120,135,150,165,180\}
4. \{1,5,15,25,30,40,60,75,100,115,130,145,160,175\}

Solución:

Recordemos que un espacio muestral es el conjunto de todos los posibles resultados en un experimento. De forma un poco abstracta, nuestro experimento es encontrar los enteros divisibles por 15 entre 1 y 180.

Un número será divisible entre 15 si y solo si es divisible entre 3 y 5 a la vez, es decir:

• Que la suma de sus dígitos sea un número múltiplo de 3
• Que termine en 0 o 5

Ya que son demasiados números para realizar la comprobación uno por uno, haremos algo más ingenioso. Las tablas de multiplicar se construyen tomando al número en cuestión y multiplicándose por la secuencia 1, 2, 3,… usualmente hasta el 10, esta vez lo haremos hasta \frac{180}{15}=12 .

M_{15}=\{15 n\}=\{15,30,45,60,75,90,105,120,135,150,165,180\}

Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).