Guía IPN 2023 Cálculo Diferencial Parte 4 del 31 al 40

¡Llegamos a la última parte aspirante! Encuentra la solución de los reactivos de cálculo diferencial desde el 31 al 40 correspondientes a la guía de estudio del IPN 2023.

¡Felicidades por llegar hasta este punto! Recuerda que puedes continuar estudiando para el resto de asignaturas con los materiales IPN 2023.

Reactivo 31

Calcular la ecuación de la recta normal a la curva y+{x}^{2}=2,\text{ en }(1, 1) .

1. y-2x=0
2. 2y+x=5
3. 2y-x=1
4. y+2x=5

Solución:

Este reactivo está mal planteado en la guía del IPN. Hemos rediseñado el enunciado para que tenga solución.

Iniciamos calculando la pendiente de la recta tangente a la curva en el punto dado. Para ello, debemos obtener la derivada de la curva.

y+{x}^{2}=2\to y=2-{x}^{2}

Derivando nos queda.

{y}^{\text{'}}=-2x

Evaluamos x=1 .

m={y}^{\text{'}}\left(1\right)=-2\left(1\right)

\therefore m=-2

Esta es la pendiente de la recta tangente, la pendiente de la normal a esta se calcula como:

{m}_{\perp }=-\frac{1}{m}=-\frac{1}{-2}=\frac{1}{2}

Con esta pendiente y el punto \left(1, 1\right) , podemos calcular la ecuación de la recta normal.

y-1=\frac{1}{2}\left(x-1\right)\to 2y-2=x-1

Simplificando:

2y-x=1

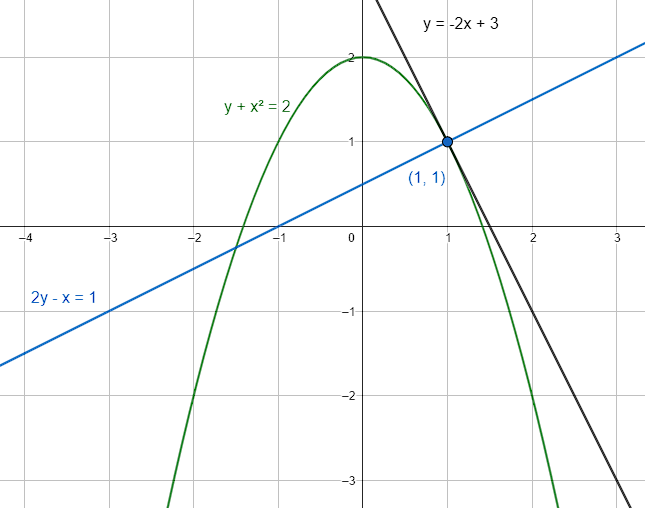
La respuesta correcta es el inciso c).

Sigue practicando la parte de cálculo diferencial:

• Parte 1: Ejercicios del 1 al 10
• Parte 2: Ejercicios del 11 al 20
• Parte 3: Ejercicios del 21 al 30

Reactivo 32

Obtener la derivada de la función:

y\left(x\right)=\frac{1}{2}{9}^{-\sqrt{1-{x}^{2}}}

1. \frac{{9}^{-\sqrt{1-{x}^{2}}}\mathrm{log}\left(9\right)}{2\sqrt{1-{x}^{2}}}
2. \frac{{9}^{-\sqrt{1-{x}^{2}}}\mathrm{log}\left(9\right)x}{\sqrt{1-{x}^{2}}}
3. \frac{{9}^{-\sqrt{1-{x}^{2}}}\mathrm{log}\left(3\right)x}{\sqrt{1-{x}^{2}}}
4. \frac{{9}^{-\sqrt{1-{x}^{2}}}\mathrm{log}\left(3\right)}{2\sqrt{1-{x}^{2}}}

Solución:

Para derivar esta función, es necesario aplicar la regla de la cadena. La función principal en este caso es la potencial, por lo que iniciamos aplicando la fórmula para derivar una función potencial.

{y}^{\text{'}}\left(x\right)={\left[\frac{1}{2}{9}^{-\sqrt{1-{x}^{2}}}\right]}^{\text{'}}=\frac{1}{2}{\left[{9}^{-\sqrt{1-{x}^{2}}}\right]}^{\text{'}}

{y}^{\text{'}}\left(x\right)=\frac{1}{2}{9}^{-\sqrt{1-{x}^{2}}}\cdot \mathrm{log}\left(9\right)\cdot {\left(-\sqrt{1-{x}^{2}}\right)}^{\text{'}}

La derivada indicada se resuelve aplicando la fórmula para una potencia.

{y}^{\text{'}}\left(x\right)=-\frac{\mathrm{log}\left(9\right)}{2}{9}^{-\sqrt{1-{x}^{2}}}\cdot \left[\frac{1}{2}\cdot {\left(1-{x}^{2}\right)}^{\frac{1}{2}-1}\cdot {\left(1-{x}^{2}\right)}^{\text{'}}\right]

{y}^{\text{'}}\left(x\right)=-\frac{\mathrm{log}\left(9\right)}{4}{9}^{-\sqrt{1-{x}^{2}}}\cdot {\left(1-{x}^{2}\right)}^{-\frac{1}{2}}\left(-2x\right)=\frac{\mathrm{log}\left(9\right)}{2}{9}^{-\sqrt{1-{x}^{2}}}\cdot \frac{x}{\sqrt{1-{x}^{2}}}

Finalmente:

{y}^{\text{'}}\left(x\right)=\frac{{9}^{-\sqrt{1-{x}^{2}}}\mathrm{log}\left(9\right)x}{2\sqrt{1-{x}^{2}}}

Para que la respuesta se asemeja a uno de los incisos, debemos simplificar al logaritmo.

{y}^{\text{'}}\left(x\right)=\frac{{9}^{-\sqrt{1-{x}^{2}}}\mathrm{log}\left({3}^{2}\right)x}{2\sqrt{1-{x}^{2}}}=2\frac{{9}^{-\sqrt{1-{x}^{2}}}\mathrm{log}\left(3\right)x}{2\sqrt{1-{x}^{2}}}=\frac{{9}^{-\sqrt{1-{x}^{2}}}\mathrm{log}\left(3\right)x}{\sqrt{1-{x}^{2}}}

\therefore {y}^{\text{'}}\left(x\right)=\frac{{9}^{-\sqrt{1-{x}^{2}}}\mathrm{log}\left(3\right)x}{\sqrt{1-{x}^{2}}}

Comparando con los incisos, concluimos que la respuesta correcta es la opción c).

Conoce todo sobre la nueva guía de ingreso al IPN

Reactivo 33

Determinar la derivada de la función:

f\left(x\right)={x}^{2}\mathrm{cos}\left(3x\right)

1. {f}^{\mathrm{\text{'}}}\left(x\right)=2x\mathrm{cos}\left(3x\right)-3{x}^{2}\mathrm{sen}\left(3x\right)
2. {f}^{\mathrm{\text{'}}}\left(x\right)=2x\mathrm{cos}\left(3x\right)+3{x}^{2}\mathrm{sen}\left(3x\right)
3. {f}^{\mathrm{\text{'}}}\left(x\right)=2x\mathrm{cos}\left(3x\right)-{x}^{2}\mathrm{sen}\left(3x\right)
4. {f}^{\mathrm{\text{'}}}\left(x\right)=3x\mathrm{c}\mathrm{o}\mathrm{s}\left(3x\right)-3{x}^{2}\mathrm{s}\mathrm{e}\mathrm{n}\left(3x\right)

Solución:

Debido a que la función es el producto de dos funciones, debemos iniciar derivando con la fórmula del producto.

{f}^{\text{'}}\left(x\right)={\left[{x}^{2}\mathrm{cos}\left(3x\right)\right]}^{\text{'}}={\left({x}^{2}\right)}^{\text{'}}\mathrm{cos}\left(3x\right)+{x}^{2}{\left[\mathrm{cos}\left(3x\right)\right]}^{\text{'}}

Aplicamos la fórmula de la derivada de una potencia y del coseno respectivamente.

{f}^{\text{'}}\left(x\right)=2x\mathrm{cos}\left(3x\right)-{x}^{2}\mathrm{sin}\left(3x\right){\left(3x\right)}^{\text{'}}

Finalmente:

{f}^{\text{'}}\left(x\right)=2x\mathrm{cos}\left(3x\right)-3{x}^{2}\mathrm{sin}\left(3x\right)

La respuesta correcta es el inciso a).

Reactivo 34

Determinar la derivada de la función:

y=\mathrm{ln}\left(\mathrm{tan}3x\right)

1. 3\mathrm{cot}3x+3\mathrm{tan}3x
2. \frac{3}{x}\mathrm{tan}3x+6\mathrm{ln}x{\mathrm{sec}}^{2}3x
3. 3\mathrm{sec}3x+6\mathrm{csc}3x
4. \frac{6}{x}{\mathrm{sec}}^{2}3x+3\mathrm{ln}\mathrm{xtan}3x

Solución:

Teniendo en cuenta la regla de la cadena, la función principal es la del logaritmo natural, por lo tanto, aplicamos la fórmula de la derivada del logaritmo natural.

{y}^{\text{'}}\left(x\right)={\left[\mathrm{ln}\left(\mathrm{tan}3x\right)\right]}^{\text{'}}=\frac{{\left(\mathrm{tan}3x\right)}^{\text{'}}}{\mathrm{tan}3x}

Ahora, aplicamos la fórmula de la derivada de la tangente.

{y}^{\text{'}}\left(x\right)=\frac{3{\mathrm{sec}}^{2}\left(3x\right)}{\mathrm{tan}3x}

Para que nuestra solución se asemeje a los incisos, debemos transformar aplicando identidades trigonométricas.

{\mathrm{tan}}^{2}\left(3x\right)+1={\mathrm{sec}}^{2}\left(3x\right)

Sustituyendo:

{y}^{\text{'}}\left(x\right)=3\frac{{\mathrm{tan}}^{2}\left(3x\right)+1}{\mathrm{tan}3x}=3\mathrm{tan}3x+3\mathrm{cot}3x

Finalmente:

{y}^{\text{'}}\left(x\right)=3\mathrm{tan}3x+3\mathrm{cot}3x

La respuesta correcta es el inciso a).

Conoce los pasos para aplicar a la universidad: Todo sobre la convocatoria del IPN.

Reactivo 35

Determinar la derivada de la función f\left(x\right)=\mathrm{ln}\left|3{x}^{2}+7\right| .

1. {f}^{\mathrm{\text{'}}}\left(x\right)=\frac{1}{3{x}^{2}+7}
2. {f}^{\mathrm{\text{'}}}\left(x\right)=\frac{3}{3{x}^{2}+7}
3. {f}^{\mathrm{\text{'}}}\left(x\right)=\frac{6}{3{x}^{2}+7}
4. {f}^{\mathrm{\text{'}}}\left(x\right)=\frac{6x}{3{x}^{2}+7}

Solución:

Para resolver la derivada de esta función con valor absoluto podemos hacer dos cosas:

• Aplicar la fórmula de la derivada del valor absoluto
• Buscar alguna simplificación

Debido a que es un caso bastante inusual, vamos a resolver el problema de ambas formas para contrastar.

Aplicando la fórmula del valor absoluto.

y=\left|f\left(x\right)\right|\to {y}^{\text{'}}=\frac{f\left(x\right)}{\left|f\left(x\right)\right|}{f}^{\text{'}}\left(x\right)

La función del enunciado tiene como función principal el logaritmo natural. Iniciamos aplicando la fórmula de la derivada del logaritmo natural.

{f}^{\text{'}}\left(x\right)=\frac{{\left|3{x}^{2}+7\right|}^{\text{'}}}{\left|3{x}^{2}+7\right|}

Ahora, aplicamos la derivada del valor absoluto.

{f}^{\text{'}}\left(x\right)=\frac{1}{\left|3{x}^{2}+7\right|}\cdot \frac{3{x}^{2}+7}{\left|3{x}^{2}+7\right|}{\left(3{x}^{2}+7\right)}^{\text{'}}=\frac{6x\left(3{x}^{2}+7\right)}{{\left|3{x}^{2}+7\right|}^{2}}

El cuadrado del valor absoluto es igual al argumento al cuadrado.

{f}^{\text{'}}\left(x\right)=\frac{6x\left(3{x}^{2}+7\right)}{{\left(3{x}^{2}+7\right)}^{2}}=\frac{6x}{3{x}^{2}+7}

Simplificación a partir de análisis.

Si observamos por un momento la función que se encuentra en el argumento del logaritmo natural, esta es positiva para todo su dominio. Podemos quitar las barras de valor absoluto porque el resultado siempre será positivo.

f\left(x\right)=\mathrm{ln}\left|3{x}^{2}+7\right|=\mathrm{ln}\left(3{x}^{2}+7\right)

Aplicamos la fórmula de la derivada del logaritmo natural.

{f}^{\text{'}}\left(x\right)=\frac{{\left(3{x}^{2}+7\right)}^{\text{'}}}{3{x}^{2}+7}=\frac{6x}{3{x}^{2}+7}

El resultado es el mismo.

La respuesta correcta es el inciso d).

Reactivo 36

Identificar la derivada \frac{df}{dx} de la función f\left(u\right)={u}^{3};\text{ si }u\left(x\right)=\frac{2}{3}{x}^{2}-4x .

1. 3{\left(\frac{2}{3}{x}^{2}-4x\right)}^{2}\left(x-4\right)
2. 4{\left(\frac{2}{3}{x}^{2}-4x\right)}^{2}\left(x-3\right)
3. 12{\left(\frac{2}{3}{x}^{2}-4x\right)}^{2}\left(\frac{1}{3}x-1\right)
4. \frac{12}{3}{\left(\frac{2}{3}{x}^{2}-4x\right)}^{2}\left(x-3\right)

Solución:

Este problema puede resolverse de dos formas: aplicando composición de funciones o mediante la regla de la cadena. Debido a que los reactivos de esta sección tienen la intensión de que apliques los conceptos del cálculo diferencial, emplearemos la regla de la cadena.

\frac{df\left(u\right)}{dx}=\frac{df\left(u\right)}{du}\times \frac{du}{dx}

Derivamos a cada función según la variable independiente que las compone.

\frac{df\left(u\right)}{du}=\frac{d\left({u}^{3}\right)}{du}=3{u}^{2}

\frac{du}{dx}=\frac{d\left(\frac{2}{3}{x}^{2}-4x\right)}{dx}=\frac{4}{3}x-4

Sustituimos u=\frac{2}{3}{x}^{2}-4x en la primera derivada.

\frac{df\left(u\right)}{du}\times \frac{du}{dx}=3{u}^{2}\left(\frac{4}{3}x-4\right)=3{\left(\frac{2}{3}{x}^{2}-4x\right)}^{2}\left(\frac{4}{3}x-4\right)

Simplificando nos queda:

\frac{df\left(u\right)}{dx}=4{\left(\frac{2}{3}{x}^{2}-4x\right)}^{2}\left(x-3\right)

La respuesta correcta es el inciso b). Tanto el inciso b) como el c) son equivalentes. Si solo extraemos factor común el 4 nos queda:

3{\left(\frac{2}{3}{x}^{2}-4x\right)}^{2}\left(\frac{4}{3}x-4\right)=12{\left(\frac{2}{3}{x}^{2}-4x\right)}^{2}\left(\frac{1}{3}x-1\right)

Tanto la opción b) como la c) son correctas.

¿Sabes cuántos puntos necesitas para quedar? Conoce los aciertos por carrera del IPN.

Reactivo 37

Determinar la derivada de la función

f\left(x\right)=\mathrm{cos}\left(\sqrt{{x}^{2}+1}\right)

1. {f}^{\mathrm{\text{'}}}\left(x\right)=-\frac{x}{\sqrt{{x}^{2}+1}}\mathrm{sen}\left(\sqrt{{x}^{2}+1}\right)
2. {f}^{\mathrm{\text{'}}}\left(x\right)=-\frac{2x}{\sqrt{{x}^{2}+1}}\mathrm{sen}\left(\sqrt{{x}^{2}+1}\right)
3. {f}^{\mathrm{\text{'}}}\left(x\right)=-\frac{x}{2\sqrt{{x}^{2}+1}}\mathrm{sen}\left(\sqrt{{x}^{2}+1}\right)
4. {f}^{\mathrm{\text{'}}}\left(x\right)=-\frac{1}{2\sqrt{{x}^{2}+1}}\mathrm{sen}\left(\sqrt{{x}^{2}+1}\right)

Solución:

Iniciamos aplicando la fórmula de la derivada del coseno.

{f}^{\text{'}}\left(x\right)={\left[\mathrm{cos}\left(\sqrt{{x}^{2}+1}\right)\right]}^{\text{'}}=-\mathrm{sin}\left(\sqrt{{x}^{2}+1}\right){\left(\sqrt{{x}^{2}+1}\right)}^{\text{'}}

Resolvemos la derivada indicada.

{f}^{\text{'}}\left(x\right)=-\mathrm{sin}\left(\sqrt{{x}^{2}+1}\right)\cdot \frac{1}{2}{\left({x}^{2}+1\right)}^{-\frac{1}{2}}\left(2x\right)=-\frac{x\mathrm{sin}\left(\sqrt{{x}^{2}+1}\right)}{\sqrt{{x}^{2}+1}}

Finalmente:

{f}^{\text{'}}\left(x\right)=-\frac{x}{\sqrt{{x}^{2}+1}}\mathrm{sin}\left(\sqrt{{x}^{2}+1}\right)

Concluimos que la respuesta correcta es el inciso a).

Reactivo 38

Utilizando la regla de la cadena, derivar la siguiente función:

f\left(x\right)=\mathrm{ln}\sqrt{1+9{x}^{2}}

1. \frac{\frac{9}{2}x}{\sqrt{1+9{x}^{2}}}
2. \frac{9x}{\sqrt{1+9{x}^{2}}}
3. \frac{9x}{\left(1+9{x}^{2}\right)}
4. \frac{9x}{\mathrm{ln}\sqrt{1+9{x}^{2}}}

Solución:

La función principal es la del logaritmo natural. Iniciamos derivando con la fórmula del logaritmo natural.

{f}^{\text{'}}\left(x\right)={\left[\mathrm{ln}\sqrt{1+9{x}^{2}}\right]}^{\text{'}}=\frac{{\left(\sqrt{1+9{x}^{2}}\right)}^{\text{'}}}{\sqrt{1+9{x}^{2}}}

Resolvemos la derivada indicada.

{f}^{\text{'}}\left(x\right)=\frac{{\left(\sqrt{1+9{x}^{2}}\right)}^{\text{'}}}{\sqrt{1+9{x}^{2}}}=\frac{\frac{1}{2}{\left(1+9{x}^{2}\right)}^{-\frac{1}{2}}{\left(1+9{x}^{2}\right)}^{\text{'}}}{\sqrt{1+9{x}^{2}}}

Simplificando nos queda:

{f}^{\text{'}}\left(x\right)=\frac{\frac{1}{2}{\left(1+9{x}^{2}\right)}^{-\frac{1}{2}}\left(18x\right)}{\sqrt{1+9{x}^{2}}}=\frac{9x}{\sqrt{1+9{x}^{2}}\sqrt{1+9{x}^{2}}}=\frac{9x}{1+9{x}^{2}}

Finalmente:

{f}^{\text{'}}\left(x\right)=\frac{9x}{1+9{x}^{2}}

La respuesta correcta es el inciso c).

Conoce la oferta académica completa del Instituto Politécnico Nacional: Lista de carreras del IPN por área.

Reactivo 39

La derivada de y=\mathrm{arctan}\left(x+3\right) es:

1. {y}^{\mathrm{\text{'}}}=\frac{1}{(x+3{)}^{2}+1}
2. {y}^{\mathrm{\text{'}}}=-\frac{1}{(x+3{)}^{2}+1}
3. {y}^{\mathrm{\text{'}}}=\frac{1}{(x+3{)}^{2}-1}
4. {y}^{\mathrm{\text{'}}}=-\frac{1}{(x+3{)}^{2}-1}

Solución:

Iniciamos aplicando la fórmula para la derivada de la arco tangente.

{y}^{\text{'}}={\left[\mathrm{arctan}\left(x+3\right)\right]}^{\text{'}}=\frac{{\left(x+3\right)}^{\text{'}}}{{\left(x+3\right)}^{2}+1}

Resolvemos la derivada indicada y simplificamos.

{y}^{\text{'}}=\frac{1}{{\left(x+3\right)}^{2}+1}

Indicamos como respuesta correcta al inciso a).

Reactivo 40

Identificar las coordenadas de los puntos máximo o mínimo de la función:

f\left(x\right)=\frac{1}{3}{x}^{3}-\frac{5}{2}{x}^{2}+4x

1. \left(-1,-\frac{41}{6}\right)\text{ máximo },\left(-4,-\frac{10}{3}\right)\text{ mínimo}
2. \left(1,\frac{11}{6}\right)\text{ máximo, }\left(4,-\frac{8}{3}\right)\text{ mínimo}
3. \left(-1,-\frac{41}{6}\right)\text{ máximo, }\left(4,-\frac{10}{3}\right)\text{ mínimo}
4. \left(1,-\frac{11}{6}\right)\text{ máximo, }\left(-4,\frac{8}{3}\right)\text{ mínimo}

Solución:

Para determinar los máximos y mínimos de una función, primero debemos calcular los números críticos de f\left(x\right) . Los cuales se obtienen al igualar a cero la primera derivada de la función.

\frac{df}{dx}=0\to {\left(\frac{1}{3}{x}^{3}-\frac{5}{2}{x}^{2}+4x\right)}^{\text{'}}=0

{x}^{2}-5x+4=0

Este trinomio se puede factorizar sin el uso de la fórmula de segundo grado. Buscamos dos números que sumados sean -5 y que multiplicados 4. Estos son: -1 y -4.

{x}^{2}-5x+4=0\to \left(x-1\right)\left(x-4\right)=0

Despejando:

{x}_{1}=1, {x}_{2}=4

Con estos valores de x , podríamos concluir que la respuesta correcta es el inciso b) porque es la única opción con estos valores de x . De igual forma, continuemos la solución. Evaluamos estos resultados en la función para obtener la ordenada del punto.

{f}_{1}\left(1\right)=\frac{1}{3}{\left(1\right)}^{3}-\frac{5}{2}{\left(1\right)}^{2}+4\left(1\right)=\frac{11}{6}\to {P}_{1}\left(1,\frac{11}{6}\right)

{f}_{2}\left(4\right)=\frac{1}{3}{4}^{3}-\frac{5}{2}{4}^{2}+4\left(4\right)=-\frac{8}{3}\to {P}_{2}\left(4,-\frac{8}{3}\right)

Ahora, para saber cual es mínimo o máximo, empleamos el criterio de la segunda derivada. Si {f}^{\text{'}\text{'}}\left(a\right)<0 el punto es un máximo relativo, en caso contrario: {f}^{\text{'}\text{'}}\left(a\right)>0 es un mínimo relativo.

Calculamos la segunda derivada.

{f}^{\text{'}\text{'}}\left(x\right)=2x-5

Evaluamos el primer número crítico.

{f}^{\text{'}\text{'}}\left(1\right)=2\left(1\right)-5=-3

{P}_{1}\left(1,\frac{11}{6}\right)\to \mathrm{m}\mathrm{á}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{o}

Evaluamos el segundo número crítico.

{f}^{\text{'}\text{'}}\left(4\right)=2\left(4\right)-5=3

{P}_{2}\left(4,-\frac{8}{3}\right)\to \mathrm{m}\mathrm{í}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{o}

Finalmente:

\left(1,\frac{11}{6}\right)\text{ máximo, }\left(4,-\frac{8}{3}\right)\text{ mínimo}

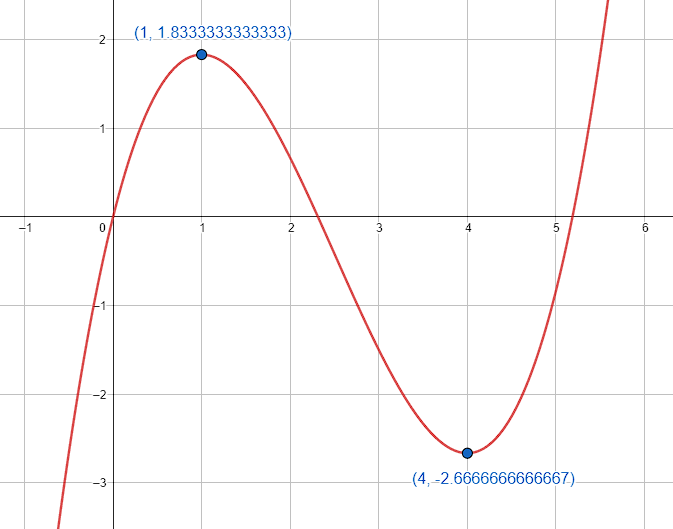
La respuesta correcta es el inciso b).