Guía IPN 2023 resuelta Álgebra – ejercicios del 11 al 20 – Parte 2

¡Hola de nuevo, aspirante! Continuamos con la segunda parte de la solución paso a paso de los reactivos de álgebra en la guía del IPN 2023. En esta segunda parte, vamos con los problemas del 11 al 20.

Desarrolla los ejercicios por tu cuenta antes de checar la solución. Utiliza esta guía resuleta como material de consulta.

Reactivo 11

En una mueblería a los productos que después de un año no se han vendido se les aplica un 50% de descuento. En la época navideña se les hace un 30% de descuento adicional y únicamente el 31 de diciembre el descuento es del 40%. ¿Cuánto se pagará por un producto que no se ha vendido en dos años el día 31 de diciembre si, originalmente costaba 1400?

1. $294
2. $210
3. $148
4. $98

Solución:

Debido a que el día en el que se realiza la compra de 1400 pesos, se encuentran válidos los tres descuentos, podemos obtener el precio final a pagar como el producto de los descuentos por el precio original.

\mathrm{P}\mathrm{F}=\mathrm{P}\mathrm{O}\left(1-D\right)

Nota: el descuento se sustituye en forma de decimal.

Debido a que el producto se encuentra en el almacén desde hace dos años, el descuento del 50% se le aplica dos veces según a lo establecido en el enunciado: a los productos que después de un año no se han vendido se les aplica un 50% de descuento.

El precio de venta pasado el primer año sería:

{\mathrm{P}\mathrm{V}}_{1}=1400\left(1-0.5\right)=700\$

Pasado el segundo año, el precio de venta sería:

{\mathrm{P}\mathrm{V}}_{2}=700\left(1-0.5\right)=350\mathrm{\$}

Finalmente, debido a que el producto se vende el 31 de diciembre, se le aplica un 40% de descuento en lugar de 30%.

\mathrm{P}\mathrm{F}\mathrm{V}=350\left(1-0.4\right)=210\$

El precio final del producto que no se ha vendido en dos años es de 210 pesos.

Concluimos indicando como respuesta correcta al inciso b).

Reactivo 12

Un grupo de 40 electricistas realiza un tendido de 20 km de cable en 35 días. Al acercarse la fecha límite de entrega deben colocar los mismos 20 km, pero en 25 días. ¿Cuántos electricistas deben contratarse para concluir a tiempo?

1. 5
2. 16
3. 20
4. 28

Solución:

Para resolver el problema, debemos aplicar una regla de tres compuesta. Se llama “compuesta” porque hay más de dos variables relacionadas. Nuestra incógnita de interés es el número de electricistas. Debemos establecer el tipo de relación entre la incógnita y el resto de variables.

Cantidad de electricistas – km de cable. La relación es directa, porque a mayor cantidad de cable más electricistas deben ser contratados.

Cantidad de electricistas – tiempo de entrega. La relación es inversa, porque a mayor cantidad de electricistas, menor tiempo tomará culminar el proyecto.

Disponemos las variables en una tabla.

Aplicamos la regla de tres compuesta:

\frac{x}{40}=\left(\frac{20}{20}\right)\left(\frac{35}{25}\right)\to x=40\left(\frac{35}{25}\right)

x=56 \mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{s}

La empresa desarrolladora del proyecto ya cuenta con 40 electricistas en su nómina, esto significa que debe contratar 16 electricistas adicionales para culminar la obra en el tiempo establecido. La respuesta correcta es el inciso b).

Reactivo 13

La expresión algebraica ____ representa al enunciado: «La duplicidad de la diferencia de dos números entre tres veces la raíz cúbica del sustraendo».

1. \frac{2}{3}\left(\frac{x}{\sqrt[3]{x}}-y\right)
2. \frac{2}{3}\left(x-\frac{y}{\sqrt[3]{y}}\right)
3. \frac{2\left(x-y\right)}{3\sqrt[3]{x}}
4. \frac{2\left(x-y\right)}{3\sqrt[3]{y}}

Solución:

Para resolver este tipo de problemas, debes conocer de antemano las equivalencias entre lenguaje natural y lenguaje algebraico. Vamos a ir analizando parte por parte de la frase hasta llegar a la expresión completa.

La duplicidad de la diferencia de dos números…

En este caso, la duplicidad se obtiene al multiplicar por 2 la resta que se enuncia a continuación. Cuando se habla de “dos números”, esto se traduce en dos variables. Por conveniencia usaremos x para el primer número y y para el segundo. Lo anterior quedaría como:

2\left(x-y\right)\dots 

…entre tres veces la raíz cúbica del sustraendo.

Debemos dividir al resultado anterior por el producto de 3 con la raíz cúbica del sustraendo. Recordando a los elementos de la resta, el minuendo es el número que resta, el que se encuentra a la derecha del signo menos. La y en nuestro caso. Esta parte se refiere a 3\sqrt[3]{y} .

\frac{2\left(x-y\right)}{3\sqrt[3]{y}}

Comparando nuestro resultado con los incisos, concluimos que la respuesta correcta se encuentra en el d).

Conoce los pasos para aplicar a la universidad: Todo sobre la convocatoria del IPN.

Reactivo 14

Identificar la expresión que representa lo dicho en el siguiente enunciado:

La raíz cuadrada del triple del cuadrado de la suma de un número par y uno impar consecutivos entre la diferencia de cuadrados de los mismos números.

1. \sqrt{3\frac{(2n{)}^{2}+(2n+1{)}^{2}}{(2n{)}^{2}-(2n+1{)}^{2}}}
2. \sqrt{\frac{3(2n+(2n+1){)}^{2}}{(2n-(2n+1\left)\right)(2n+(2n-1\left)\right)}}
3. \sqrt{\frac{3(2n+(2n+1){)}^{2}}{(2n{)}^{2}-(2n+1{)}^{2}}}
4. \sqrt{3\frac{(2n{)}^{2}+(2n+1{)}^{2}}{(2n-(2n+1\left)\right)(2n+(2n-1\left)\right)}}

Solución:

Debemos analizar con cuidado las relaciones que establece el enunciado. Sabemos que a toda la expresión se le va a aplicar raíz cuadrada y que el interior va a ser multiplicado por 3. Eso lo extraemos de la primera parte de la frase: La raíz cuadrada del triple…

\sqrt{3\left(\frac{}{}\right)\dots }

…del cuadrado de la suma de un número par y uno impar consecutivos entre…

Cuando queremos calcular un número par dada una secuencia de n números naturales 1, 2, 3, \dots  lo que hacemos es multiplicar a n por 2. Es decir, el número par se obtiene como 2n . Por otro lado, los impares se consiguen sumando 1 a los pares, es decir: 2n+1 .

Tenemos la suma de ambas cantidades: 2n+\left(2n+1\right) , elevada al cuadrado.

{\left[2n+\left(2n+1\right)\right]}^{2}

Escribiendo la expresión completa nos va quedando:

\sqrt{3\frac{{\left[2n+\left(2n+1\right)\right]}^{2}}{\dots }}

…entre la diferencia de cuadrados de los mismos números.

La diferencia de cuadrados establece que vamos a expresar al cuadrado del par menos el cuadrado del impar. Tal cuál como el producto notable que lleva el mismo nombre: {a}^{2}-{b}^{2} . En esta ocasión: {\left(2n\right)}^{2}-{\left(2n+1\right)}^{2}

\sqrt{3\frac{{\left[2n+\left(2n+1\right)\right]}^{2}}{{\left(2n\right)}^{2}-{\left(2n+1\right)}^{2}}}

Comparando con los incisos, indicamos al c) como la respuesta correcta.

Conoce la oferta académica completa del IPN

Reactivo 15

Elegir el par de números que cumplen con el planteamiento:

La suma del primero más la mitad del segundo es igual a 21 y la suma de la tercera parte negativa del segundo número más el doble del primero es igual a 18.

1. 10 y 12
2. 12 y 18
3. 18 y 22
4. 22 y 30

Solución:

Debido a que tenemos dos relaciones indicadas por el enunciado y conectadas a través de “y”, el reactivo nos plantea un sistema de ecuaciones en lenguaje natural. Iniciamos llevando a lenguaje algebraico a las expresiones. El primer número será x y el segundo y .

La suma del primero más la mitad del segundo es igual a 21.

x+\frac{y}{2}=21

…la suma de la tercera parte negativa del segundo número más el doble del primero es igual a 18.

2x-\frac{y}{3}=18

El sistema de ecuaciones sería:

\left\{\begin{array}{c}x+\frac{y}{2}=21\\ 2x-\frac{y}{3}=18\end{array}\right.

Eliminamos las fracciones de las ecuaciones multiplicando por 2 y por 3 respectivamente.

\left\{\begin{array}{c}x+\frac{y}{2}=21\\ 2x-\frac{y}{3}=18\end{array}\right.\to \left\{\begin{array}{c}2x+y=42\\ 6x-y=54\end{array}\right.

Sumamos las ecuaciones.

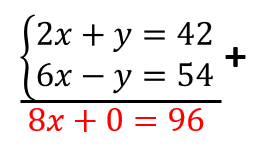
8x=96\to x=12

El único inciso que asocia al primer número 12 es el b).

La respuesta correcta es el inciso b).

Reactivo 16

Un legislador en la cámara baja propone un modelo de bienestar ( {B}_{E} ) para un habitante promedio. Este señala que el bienestar es inversamente proporcional al cuadrado de la edad del individuo (E), directamente proporcional al cubo de su salario (s) y directamente proporcional a los años que lleva casado (A). ¿Qué ecuación representa a {B}_{E} en términos de variables si \gamma  involucra las constantes de proporcionalidad?

1. {B}_{E}=\gamma \left({E}^{2}+{s}^{3}+\frac{1}{A}\right)
2. {B}_{E}=\gamma {E}^{2}{s}^{3}A
3. {B}_{E}=\gamma \frac{{E}^{2}}{{s}^{3}}A
4. {B}_{E}=\gamma \frac{{s}^{3}A}{{E}^{2}}

Solución:

En este problema de lenguaje natural matemático, debemos ir analizando lo que nos dice el reactivo con los incisos para descartar y seleccionar la respuesta correcta.

Sabemos que el modelo de bienestar es la variable dependiente {B}_{E} del modelo matemático por lo que la función inicia:

{B}_{E}=\dots 

En la siguiente frase nos indican que el bienestar es inversamente proporcional (es decir, el inverso multiplicativo) del cuadrado de la edad E . Esto se escribiría como:

{B}_{E}=\frac{\dots }{{E}^{2}}

El único inciso que tiene en el denominador al cuadrado de la edad es el d).

Indicamos como respuesta correcta al inciso d).

Lista completa de aciertos mínimos para entrar al IPN

Reactivo 17

Identificar el resultado de la resta:

\frac{3}{{x}^{2}-5}-5

1. \frac{28-5{x}^{2}}{{x}^{2}-5}
2. \frac{8-5{x}^{2}}{{x}^{2}-5}
3. \frac{18-5{x}^{2}}{{x}^{2}-5}
4. \frac{28-5{x}^{2}}{{x}^{2}-25}

Solución:

Resolvemos la resta de fracciones con distinto denominador. Rellenamos con 1 al denominados del sustraendo y resolvemos.

\frac{3}{{x}^{2}-5}-\frac{5}{1}=\frac{3-5\left({x}^{2}-5\right)}{{x}^{2}-5}

Simplificamos.

\frac{3-5\left({x}^{2}-5\right)}{{x}^{2}-5}=\frac{3-5{x}^{2}+25}{{x}^{2}-5}=\frac{28-5{x}^{2}}{{x}^{2}-5}

Examinando a los incisos, concluimos que la respuesta correcta es el a).

Reactivo 18

Simplificar la siguiente suma de fracciones:

\frac{2}{x-2}-\frac{3x}{x+2}

1. \frac{3{x}^{2}+8x+4}{{x}^{2}-4}
2. \frac{3{x}^{2}+8x-4}{{x}^{2}-4}
3. \frac{-3{x}^{2}+8x+4}{{x}^{2}-4}
4. \frac{3{x}^{2}-8x+4}{{x}^{2}-4}

Solución:

Multiplicamos cruzado a los numeradores con los denominadores y de forma lineal a los denominadores.

\frac{2}{x-2}-\frac{3x}{x+2}=\frac{2\left(x+2\right)-3x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}

Simplificamos las distributivas y aplicamos diferencia de cuadrados en el numerador.

\frac{2\left(x+2\right)-3x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{2x+4-3{x}^{2}+6x}{{x}^{2}-4}=\frac{-3{x}^{2}+8x+4}{{x}^{2}-4}

Finalmente:

\frac{2}{x-2}-\frac{3x}{x+2}=\frac{-3{x}^{2}+8x+4}{{x}^{2}-4}

La respuesta correcta es el inciso c).

Reactivo 19

Racionalizar la expresión fraccionaria:

\frac{x-2}{\sqrt{x}-\sqrt{2}}

1. \sqrt{x}-\sqrt{2}
2. \sqrt{x}+\sqrt{2}
3. x-2
4. x+2

Solución:

Para racionalizar el denominador de una fracción en forma de binomio y cuyos términos tienen raíces cuadradas, se procede a multiplicar y dividir por el conjugado del denominador a toda la fracción.

El conjugado en este caso sería: \sqrt{x}+\sqrt{2} .

\frac{x-2}{\sqrt{x}-\sqrt{2}}\cdot \frac{\sqrt{x}+\sqrt{2}}{\sqrt{x}+\sqrt{2}}=\frac{\left(x-2\right)\left(\sqrt{x}+\sqrt{2}\right)}{\left(\sqrt{x}-\sqrt{2}\right)\left(\sqrt{x}+\sqrt{2}\right)}

En el denominador aplicamos diferencia de cuadrados en sentido inverso: \left(a-b\right)\left(a+b\right)={a}^{2}-{b}^{2} .

\frac{\left(x-2\right)\left(\sqrt{x}+\sqrt{2}\right)}{\left(\sqrt{x}-\sqrt{2}\right)\left(\sqrt{x}+\sqrt{2}\right)}=\frac{\left(x-2\right)\left(\sqrt{x}+\sqrt{2}\right)}{{\left(\sqrt{x}\right)}^{2}-{\left(\sqrt{2}\right)}^{2}}

\frac{\left(x-2\right)\left(\sqrt{x}+\sqrt{2}\right)}{x-2}=\sqrt{x}+\sqrt{2}

Finalmente:

\frac{x-2}{\sqrt{x}-\sqrt{2}}=\sqrt{x}+\sqrt{2}

Concluimos indicando como respuesta correcta al inciso b).

Reactivo 20

Simplificar la expresión mediante las leyes de exponentes:

\frac{300\times {10}^{6}}{\sqrt{10\times {10}^{4}}\cdot \sqrt{100\times {10}^{7}}}

1. 30
2. 300
3. 3\times {10}^{-4}
4. \frac{3\times {10}^{2}}{\sqrt{\times {10}^{7}}}

Solución:

El trabajo de simplificación se encuentra en el denominador. Iniciamos uniendo ambas raíces cuadradas.

\frac{300\times {10}^{6}}{\sqrt{10\times {10}^{4}}\cdot \sqrt{100\times {10}^{7}}}=\frac{300\times {10}^{6}}{\sqrt{10\times {10}^{4}\times 100\times {10}^{7}}}

Resolvemos a los productos entre las potencias por un lado y entre los números enteros por otro.

\frac{300\times {10}^{6}}{\sqrt{10\times {10}^{4}\times 100\times {10}^{7}}}=\frac{300\times {10}^{6}}{\sqrt{1000\times {10}^{11}}}

Expresamos al 1000 como potencia y lo multiplicamos con el {10}^{11} .

\frac{300\times {10}^{6}}{\sqrt{1000\times {10}^{11}}}=\frac{300\times {10}^{6}}{\sqrt{{10}^{3}\times {10}^{11}}}=\frac{300\times {10}^{6}}{\sqrt{{10}^{14}}}

Expresamos a la raíz cuadrada en forma de potencia y luego simplificamos.

\frac{300\times {10}^{6}}{\sqrt{{10}^{14}}}=\frac{300\times {10}^{6}}{{10}^{\frac{14}{2}}}=\frac{300\times {10}^{6}}{{10}^{7}}

Ahora simplificamos a las potencias de base 10 aplicando la propiedad del cociente de potencias de igual base.

\frac{300\times {10}^{6}}{{10}^{7}}=300\times {10}^{6}\times {10}^{-7}=300\times {10}^{6}\times {10}^{-7}=300\times {10}^{-1}

Expresamos ahora el {10}^{-1} como \frac{1}{10} .

300\times {10}^{-1}=\frac{300}{10}=30

Finalmente:

\frac{300\times {10}^{6}}{\sqrt{10\times {10}^{4}}\cdot \sqrt{100\times {10}^{7}}}=30

Comparando con los incisos, concluimos indicando como respuesta correcta al a).