El Razonamiento matemático es una de las tantas áreas del campo de la matemática en las cuales serás evaluado al presentar el examen de admisión del IPN. Por eso es tan importante que te prepares al respecto. En vista de ello, hemos decidido resolver todos los ejercicios de la guía de matemáticas del IPN, por lo que podrás guiarte y estudiar con anticipación.

En este caso, nos encontramos en la tercera parte de nuestra serie de post dedicados al Razonamiento Matemático. Concretamente, abordaremos los ejercicios que van del número 21 al 30. Ten presente que la clave del éxito para este examen recae sobre la preparación y el estudio tanto de las matemáticas, como las demás áreas en las que serás evaluado en el examen del IPN.
¿Qué viene en el examen del IPN?
En cada convocatoria del Instituto Politécnico Nacional, los aspirantes deben presentar un examen de admisión compuesto de un total de 130 preguntas. Dichas preguntas se desgranan entre cinco áreas de estudio diferentes. La primera mitad del examen aborda conocimientos de Matemáticas y Comunicación. Seguidamente, la segunda parte se concentra en el estudio de Física, Química y Biología.
Para que tengas una idea más clara de cómo es este examen y qué tan importante es cada una de estas áreas en las cuales debes prepararte, te dejamos con la cantidad de reactivos que encontrarás en cada una de las mencionadas áreas:
- 50 preguntas de matemáticas.
- 40 preguntas de comunicación.
- 10 preguntas de biología.
- 15 preguntas de química.
- 15 preguntas de física.
Sin más que añadir, queremos que te concentres en lo importante, así que aquí tienes la tercera parte de nuestra guía resuelta de ejercicios de Razonamiento Matemático del IPN:
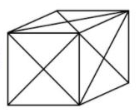
Reactivo 21: Triángulos formados
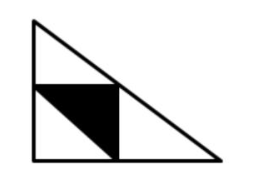
Si se corta la hipotenusa de un triángulo rectángulo en su punto medio y se traza otro triángulo rectángulo, como se muestra en la figura, después de hacer este procedimiento dos veces más ¿Cuántos triángulos se obtienen?
- 4
- 5
- 10
- 13
Solución:
Entendamos lo que describe el problema antes de pasar a contar los triángulos que se forman. Observemos que partimos de un primer triángulo rectángulo y desde el punto medio de su hipotenusa trazamos otro triángulo rectángulo, el de color negro.
Pero no solo se forma ese triángulo negro, también lo hacen 3 más de color blanco. Es decir, de 1 triángulo obtenemos 4, cuya suma es de 5.
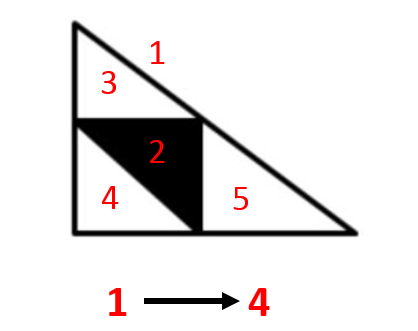
El siguiente corte no se realiza en los 4 triángulos, sino sobre el triángulo formado en el primer corte, es decir sobre el triángulo negro.

A partir de uno de los 4 triángulos anteriores, se forman 4 triángulos nuevos. El siguiente y último corte se hace de la misma forma, se toma el triángulo base y se corta para formar 4 triángulos más.
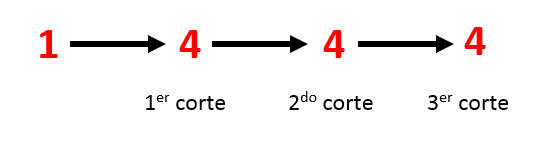
La cantidad total de triángulos formados es:
T_{t}=1+4+4+4=13
Comparando con las opciones del problema, la respuesta correcta es la d).
[wpipa id=»6649″]Reactivo 22: Número de cuadritos
Si se continúa rellenando la cuadrícula diagonalmente como se muestra en la figura ¿Cuántos cuadritos se rellenaran en una cuadrícula 11×11?

- 46
- 48
- 49
- 50
Solución:
Podemos darnos cuenta que la cuadricula en este momento es 10×10 y que el número de cuadritos negros es un cuadro 3×3 en la esquina superior izquierda, es decir 9 cuadritos. El resto se rellena siguiendo un patrón de 5 cuadritos en dirección de la esquina inferior derecha.
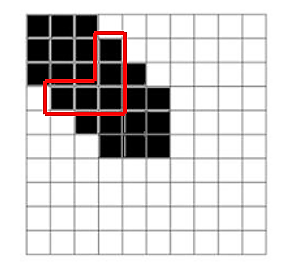
Para rellenar la cuadrícula 10×10 se necesita repetir este patrón 7 veces, las tres que ya están pintadas y 4 más. Esto se puede expresar como:
C N_{10 x 10}=9+7 * 5=44
Una cuadrícula 11×11 es igual a una 10×10 con una fila y una columna adicional, lo que ocasiona que el patrón de 5 cuadritos en diagonal se tenga que repetir una vez más, por tanto:
C N_{11 x 11}=C N_{10 \times 10}+5=44+5=49
En una cuadricula 11×11 se deben rellenar 49 cuadritos negros. Comparando con las opciones, la respuesta correcta es la c).
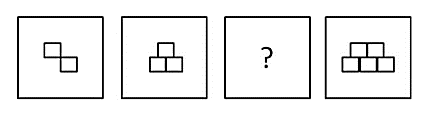
Reactivo 23: Secuencias gráficas
¿Qué figura ocupa la tercera posición?
Solución:
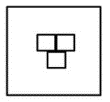
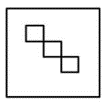
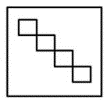
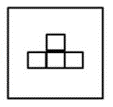
En esta secuencia se pueden identificar 2 transformaciones entre términos. La primera, es que la cantidad de cuadrados blancos aumenta en 1. El primer término posee 2, el segundo 3, el tercero debe tener 4 y el cuarto término tiene 5 cuadrados blancos.
La segunda transformación, es que los cuadrados pasan de disponerse en diagonal a apilarse. En el primer término diagonal, el segundo apilados y en el cuarto apilados. Siguiendo esta secuencia, en el tercero deben disponerse en diagonal.
Sintetizando todo el análisis, la figura del término faltante debe tener 4 cuadrados blancos con disposición en diagonal. Comparando con las opciones del problema, la respuesta correcta es la c).
Reactivo 24: Arreglo de números
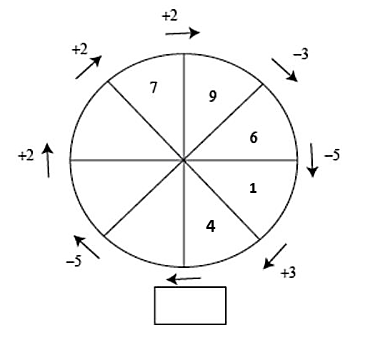
En la figura se tiene un arreglo circular de números. Cada número se construye a partir del anterior con la operación indicada en la flecha correspondiente ¿Cuál es la operación que falta en el espacio que está junto a la flecha de abajo?
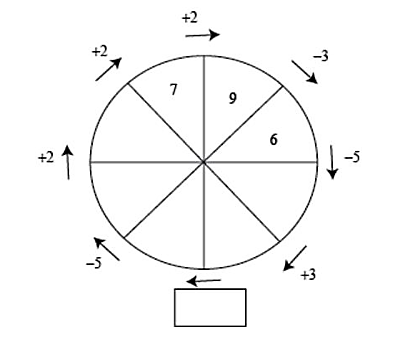
- +4
- +2
- -3
- -5
Solución:
Para determinar la operación en el cuadro indicado, debemos rellenar los espacios vacíos en el arreglo circular. Comencemos desde el 6 siguiendo la dirección de la flecha correspondiente.
La operación para obtener el siguiente número partiendo del 6 es 6-5=1 .
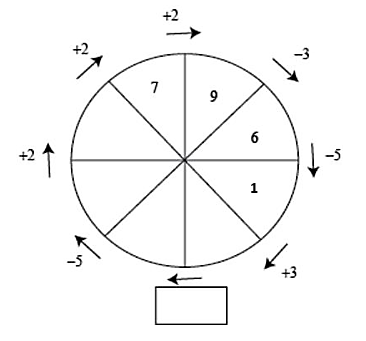
El siguiente se obtiene mediante la operación 1+3=4 .
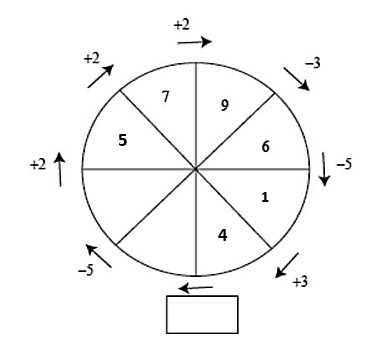
Cómo hemos llegado al cuadro con la operación desconocida, hacemos el mismo procedimiento pero en sentido contrario partiendo desde el 7. El número antes del 7 era dos unidades más pequeño, es decir 7-2=5 .
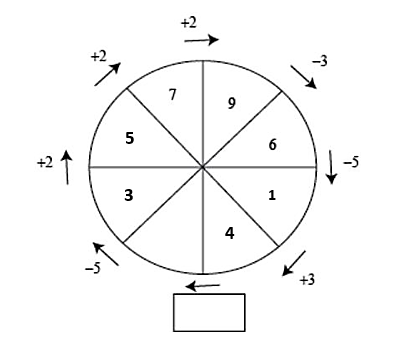
De igual forma, el número antes del 5 era dos unidades más pequeño, 5-2=3 .
El número antes del tres es 5 unidades más grande, 3+5=8 .
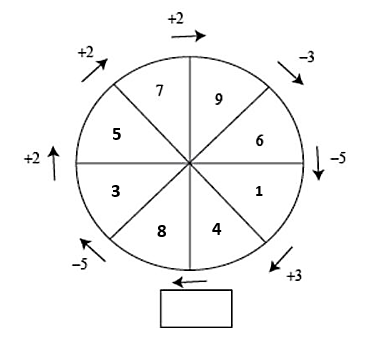
Ahora, queda claro que la operación para pasar del 4 al 8 es +4.
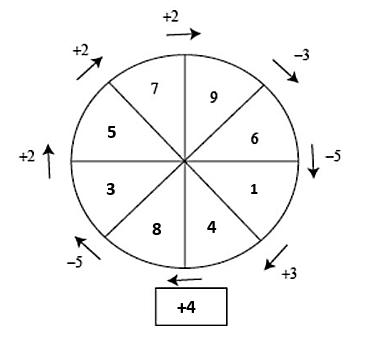
Comparando con las opciones del problema, seleccionamos como correcta a la a).
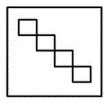
Reactivo 25: Vista superior de una figura
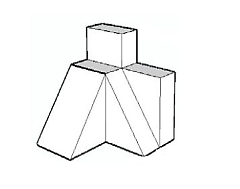
Identificar cual es la vista superior de la siguiente figura.
Solución:
Este problema se basa en la memoria espacial para encontrar la vista superior de la figura en 3 dimensiones. Primero, debemos identificar los topes en la base de la figura, los límites y las conexiones entre partes.
La rampa frontal llega a la misma altura que la meseta rectangular, dicha meseta tiene las mismas dimensiones que el siguiente escalón pero con altura diferente. La rampa del costado llega a la base de la figura al mismo punto que la pieza rectangular trasera, lo mismo ocurre con el tope superior de la rampa.
La pieza con base rectangular trasera parece tener las mismas dimensiones que los dos escalones y es congruente con el escalón más alto.
Desde arriba, las rampas deben verse como rectángulos y los escalones deben tener ancho y largo iguales, además no debe notarse la diferencia de altura. Comparando con las opciones, la vista correspondiente es la a).
Reactivo 26: Figura y patrón
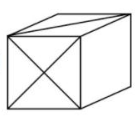
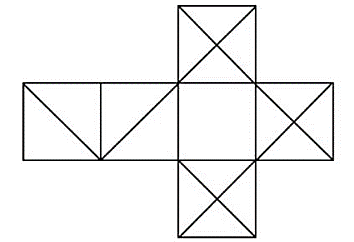
Al doblar el siguiente patrón ¿Qué cubo se obtiene?
Solución:
Para escoger la opción correcta, debemos identificar como deberían quedar dispuestas unas caras con otras a partir de los incisos dados por el problema.
Tomemos como referencia la cara frontal de cada opción y si luego de doblar, las otras dos caras corresponden a la de la opción ese es el cubo correcto.
Opción A.
La cara frontal posee una “x”, en el patrón hay 3 caras con una “x”. Si se toma como referencia la cara más baja del patrón, se dobla y se coloca al frontal, obtendremos que la cara lateral es la blanca y la superior la que tiene una línea diagonal.
El sentido de la diagonal toca la esquina superior izquierda en la cara con “x” en el cubo de la opción a, tal cual como quedaría al doblar el patrón y disponerlo en esa posición.
Respuesta tentativa a).
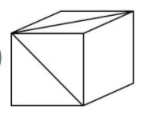
Opción B.
Las caras con líneas diagonales en el patrón nunca tendrán esa disposición respecto a la cara vacía, ya que una de las caras en diagonal es siempre opuesta a la cara vacía.
Opción C.
Esta opción se puede descartar de inmediato, porque las caras con “x” en el patrón son consecutivas en una misma dirección al doblar el cubo.
Opción D.
Esta última opción también puede descartarse por completo, ya que en el patrón solo hay dos caras con una línea diagonal.
Concluimos finalmente que la respuesta correcta es la a).
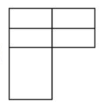
Reactivo 27: Vista lateral de una figura
Identificar la vista lateral derecha que corresponde a la imagen:

Solución:
La vista lateral derecha debe tener el mismo nivel, exceptuando por el pilar que sobresale de la base. Además, debe distinguirse la rampa como una línea diagonal que va desde la base hasta antes del pilar.
Entre las opciones del problema, la que concuerda con la descripción basada en el análisis es la a).
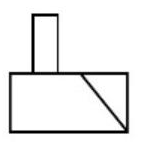
Reactivo 28: Volumen del Prisma
Indicar cuál de las siguientes opciones representa el volumen en \mathrm{cm}^{3} del prisma que se forma en la siguiente figura.
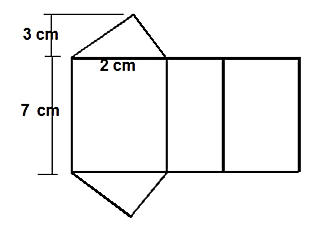
- 21
- 35
- 40
- 42
Solución:
La complejidad en este problema, radica en comprender que el prisma al que hace referencia el enunciado se encuentra “desarmado” en la figura. Solo nos muestran el patrón con el que se arma el prisma. Si se mira detenidamente, los triángulos son las bases del prisma y las secciones rectangulares de sus caras.
Para calcular el volumen, debemos determinar el área de la base del prisma y luego multiplicarla por la altura del mismo. Como la base es triangular, el área se calcula como:
A_{b}=\frac{b h}{2}
De la imagen sabemos que la altura del triángulo es 3 cm y la base es 2 cm. Sustituimos y calculamos.
A_{b}=\frac{(2)(3)}{2}=3 \mathrm{~cm}^{2}
Multiplicando ahora por la altura, obtenemos que el volumen del prisma es:
V_{p}=A_{b} \times h_{p}=\left(3 \mathrm{~cm}^{2}\right)(7 \mathrm{~cm})=21 \mathrm{~cm}^{3}
Comparando con las opciones, la respuesta correcta es la a).
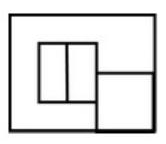
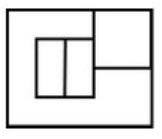
Reactivo 29: Composición de figuras
Identificar cuáles son las tres figuras que permiten formar un tablero de 5×3 cuadrados.
Solución:
Ya que el tablero debe ser 5×3, la cantidad de cuadrados que debe tener es 15. Podemos emplear este número como ayuda para identificar qué incisos tienen las combinaciones de figuras correctas.
En la figura del inciso a) hay 14 cuadrados distribuidos entre las tres formas, queda descartada. La figura b) y c) hay 18 cuadrados distribuidos en las 3 formas, sobran 3 cuadrados por tanto quedan descartadas ambas. La figura del inciso d) posee exactamente 15 cuadros entre las tres formas, es la correcta.
Concluimos entonces indicando que la figura correcta es la del inciso d).
[wpipa id=»6866″]Reactivo 30: Vértices de poliedros regulares
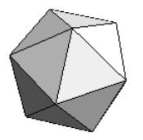
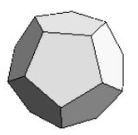
Jerarquizar de menor a mayor los siguientes poliedros regulares de acuerdo con el número total de sus vértices.
- 1, 3, 2, 4
- 1, 4, 3, 2
- 2, 1, 3, 4
- 2, 4, 3, 1
Solución:
Los sólidos en los incisos pertenecen a la familia de sólidos platónicos, donde tanto sus caras como los ángulos internos entre lados son iguales. Respectivamente son: hexaedro o cubo, octaedro, dodecaedro e icosaedro.
De los temas referentes a geometría de cuerpos sólidos, sabemos que: el cubo tiene 8 vértices, el octaedro posee 6 vértices, el dodecaedro 20 y el icosaedro 12. Ordenando de forma ascendente nos queda:
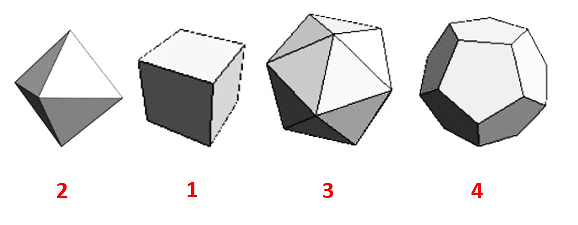
Comparando con las opciones del problema, la respuesta correcta es la c).