Guía IPN 2023 Cálculo Diferencial Parte 3 del 21 al 30

¡Hola de nuevo, aspirante! Seguimos con la solución de los reactivos de cálculo diferencial de la guía del IPN. En este caso, desarrollamos paso a paso los reactivos del el 21 al 30.

¿Te parecen complejos los reactivos? ¡No te preocupes! A lo largo de las soluciones te mencionamos algunos hacks efectivos para acortar el tiempo de solución. Únete al curso y accede a todo el contenido exclusivo.

Reactivo 21

Identificar los intervalos donde la función es continua:

f\left(x\right)=\frac{x}{{x}^{3}-5x}

1. \left(-\mathrm{5,5}\right)
2. \left(-\mathrm{\infty },5\right)\cup \left(-\mathrm{5,5},\right)\cup \left(5,\mathrm{\infty }\right)
3. \left(-\mathrm{\infty },\sqrt{5}\right)\cup \left(-\sqrt{5},\sqrt{5},\right)\cup \left(\sqrt{5},\mathrm{\infty }\right)
4. \left(-\mathrm{\infty },\sqrt{5}\right)\cup \left(-\sqrt{5},0\right)\cup \left(0,\sqrt{5}\right)\cup \left(\sqrt{5},\mathrm{\infty }\right)

Solución:

Una función es continua en un intervalo, si es continua en todos sus puntos. Además, dicho intervalo de continuidad puede ser cerrado o abierto, según si la función es continua en los extremos del intervalo.

Iniciemos calculando el dominio de f\left(x\right) .

f\left(x\right)=\frac{x}{{x}^{3}-5x}

La función existe siempre que:

{x}^{3}-5x\ne 0\to x\left({x}^{2}-5\right)\ne 0

Esta desigualdad puede descomponerse en dos:

x\ne 0, {x}^{2}-5\ne 0

Resolvemos la segunda desigualdad.

{x}^{2}-5\ne 0\to {x}^{2}\ne 5\to x\ne \pm \sqrt{5}

Finalmente:

\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=R-\left\{-\sqrt{5},0,\sqrt{5}\right\}

Escrito en forma de conjunto:

\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=\left(-\infty ,-\sqrt{5} \right)\cup \left(-\sqrt{5}, 0\right)\cup \left(0, \sqrt{5}\right)\cup \left(\sqrt{5}, \infty \right)

No es necesario comprobar los extremos de los intervalos, porque la función no está definida en ellos, por lo tanto, rompe una de las condiciones necesarias para la continuidad de la función. Concluimos entonces que f\left(x\right) es continua en:

\left(-\infty ,-\sqrt{5} \right)\cup \left(-\sqrt{5}, 0\right)\cup \left(0, \sqrt{5}\right)\cup \left(\sqrt{5}, \infty \right)

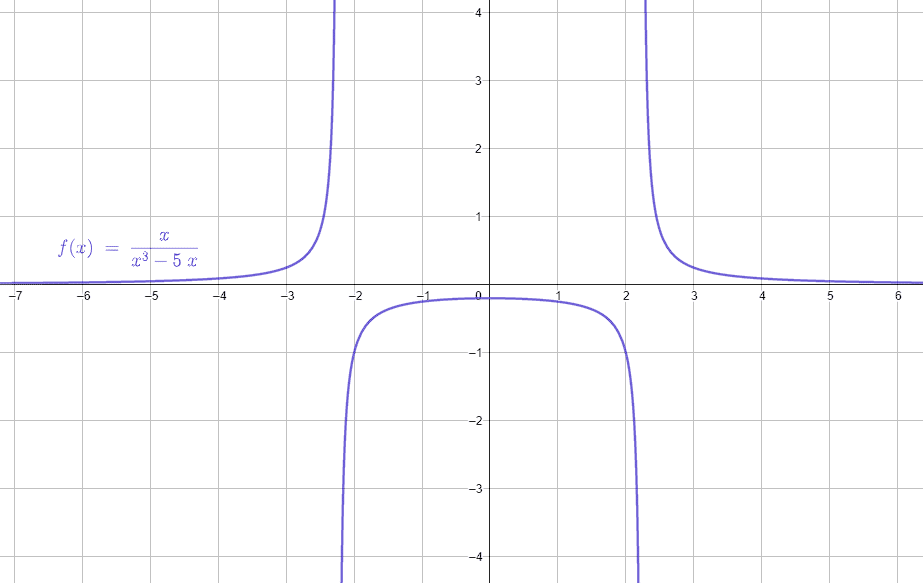
Seleccionamos como respuesta correcta al inciso d).

Reactivo 22

Determinar los valores de x para los cuales es discontinua la función:

f\left(x\right)=\frac{1}{{x}^{3}+2{x}^{2}-3x}

1. {x}_{1}=1,{x}_{2}=-1,{x}_{3}=3
2. {x}_{1}=1,{x}_{2}=-1,{x}_{3}=-3
3. {x}_{1}=0,{x}_{2}=1,{x}_{3}=3
4. {x}_{1}=0,{x}_{2}=1,{x}_{3}=-3

Solución:

Una función es discontinua en un punto cuando:

• La función no se encuentra definida en x=a
• El límite de la función en el punto no existe o, los límites laterales son distintos
• La función evaluada en el punto y el límite son distintos

Debido a que se trata de una función racional, la función es discontinua en los puntos donde se anula el denominador y, por ende, la función deja de estar definida.

Igualamos a cero el denominador.

{x}^{3}+2{x}^{2}-3x=0\to x\left({x}^{2}+2x-3\right)=0

El trinomio puede factorizarse de forma directa. Buscamos dos números que sumados sean 2 y multiplicados -3, estos son: -1 y 3.

x\left({x}^{2}+2x-3\right)=0\to x\left(x-1\right)\left(x+3\right)=0

Finalmente, la función es discontinua en:

x=0, x=1, x=-3

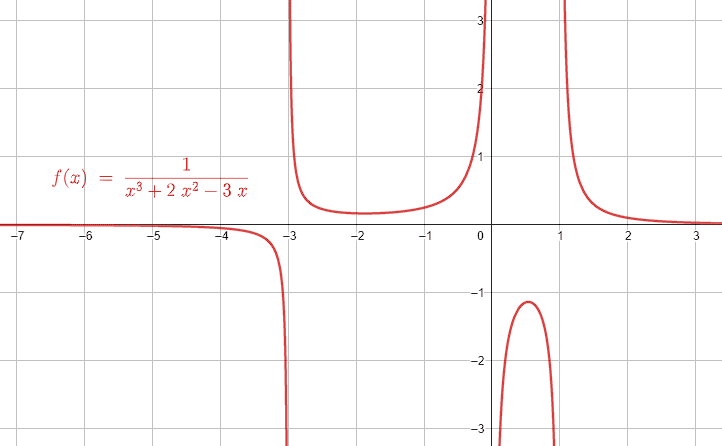
La respuesta correcta es el inciso d).

Reactivo 23

Una función f(x) continua en un punto a, no siempre es _____ en a.

1. continua
2. derivable
3. discontinua
4. infinitamente derivable

Solución:

La continuidad y la diferenciabilidad, son conceptos que van muy de la mano en el estudio de funciones. El que una función sea diferenciable en un punto, implica que la misma es también continua, pero no al contrario.

Supongamos que tenemos un punto de estudio x=a en el que la función existe y se encuentra definida. f\left(x\right) es continua en x=a si el límite existe y es igual a f\left(a\right) .

Por otra parte, f\left(x\right) será diferenciable si las derivadas laterales son iguales, es decir, si la razón de cambio antes y después de x=a es igual. Un ejemplo de continuidad, pero no diferenciabilidad es la función valor absoluto.

f\left(x\right)=\left|x\right|

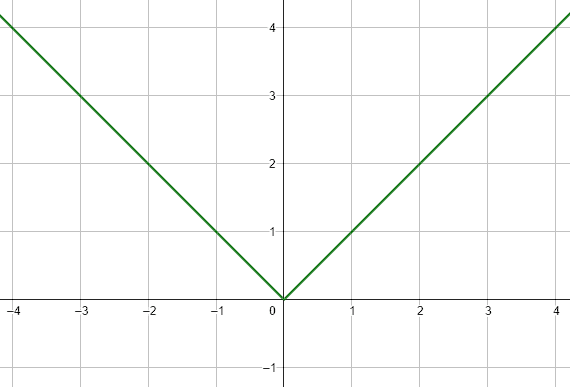
Esta función es continua en x=0 pero no es diferenciable. Antes de x=0 la derivada de la función es -1, pero después es igual a 1. Otro ejemplo más sofisticado es la función de Weierstrass.

f\left(x\right)=\sum _{n=0}^{\infty }{a}^{n}\mathrm{cos}\left({b}^{n}x\right)

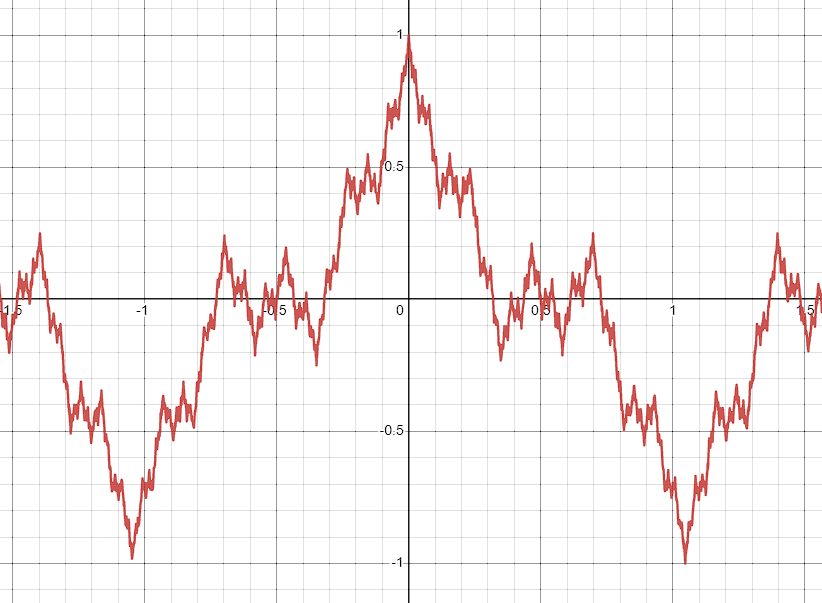
Una función continua en todo su dominio, pero no es diferenciable en ninguno. Finalmente:

Una función f(x) continua en un punto a, no siempre es derivable en a.

La respuesta correcta es el inciso b).

Reactivo 24

Señalar los criterios ordenados correctamente que debe cumplir una función f(x) para que sea continua.

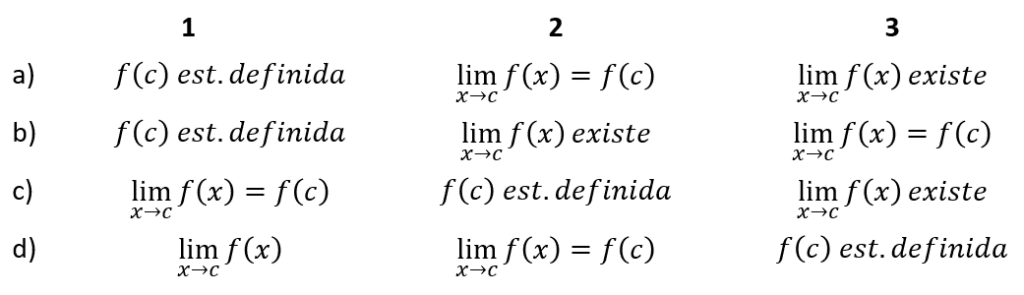
Solución:

Las condiciones para que una función sea continua son:

1. La función debe estar definida en el punto.
2. El límite de la función en el punto debe existir
3. El límite y la función evaluada en el punto deben ser iguales

El inciso que muestra esta combinación es el b). La respuesta correcta es el inciso b).

Reactivo 25

Calcular el valor de A para que la función:

s\left(x\right)=\left\{\begin{array}{c}{x}^{3}+\frac{9}{2}{x}^{2}+\frac{3}{2}Ax-2,x\le 1\\ 6+Ax-{x}^{2},x>1\end{array}\right.

sea continua en el punto x=1 .

1. 1
2. 3
3. 5
4. 9

Solución:

La función dada por el enunciado es a trozos. Desde -\infty  hasta 1 la función es {x}^{3}+\frac{9}{2}{x}^{2}+\frac{3}{2}Ax-2 y para 1 hasta \infty  , la función está definida por 6+Ax-{x}^{2} .

La condición para que la función a trozos sea continua en x=1 , es que las funciones {x}^{3}+\frac{9}{2}{x}^{2}+\frac{3}{2}Ax-2 y 6+Ax-{x}^{2} , sean iguales. Evaluamos e igualamos.

{\left(1\right)}^{3}+\frac{9}{2}{\left(1\right)}^{2}+\frac{3}{2}A\left(1\right)-2=6+A\left(1\right)-{\left(1\right)}^{2}

1+\frac{9}{2}+\frac{3}{2}A-2=6+A-1\to \frac{11}{2}+\frac{3}{2}A-2=5+A

\frac{3}{2}A-A=5+2-\frac{11}{2}

\frac{A}{2}=\frac{3}{2}\to A=3

Para que la función a trozos sea continua en x=1 , el parámetro A debe ser igual a 3.

s\left(x\right)=\left\{\begin{array}{c}{x}^{3}+\frac{9}{2}{x}^{2}+\frac{9}{2}x-2,x\le 1\\ 6+3x-{x}^{2},x>1\end{array}\right.

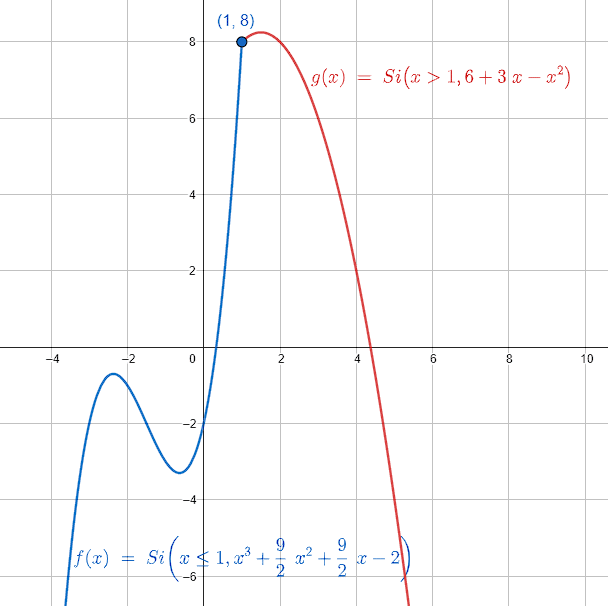
La respuesta correcta es el inciso b).

Reactivo 26

Derivar el polinomio p\left(t\right)=\left({t}^{2}-9\right)(t+4) .

1. {p}^{\mathrm{\text{'}}}\left(t\right)=3\left({t}^{2}-3\right)+8
2. {p}^{\mathrm{\text{'}}}\left(t\right)=3{t}^{2}+9t-8
3. {p}^{\mathrm{\text{'}}}\left(t\right)=3{t}^{2}+8t-9
4. {p}^{\mathrm{\text{'}}}\left(t\right)=2\left({t}^{2}-3\right)t

Solución:

Podemos desarrollar el producto o derivar la función tal como se muestra en el enunciado. Debido a que en ambos casos hay que hacer un desarrollo algebraico, vamos a derivar la función tal como se muestra.

{p}^{\text{'}}\left(t\right)={\left[\left({t}^{2}-9\right)\left(t+4\right)\right]}^{\text{'}}

Aplicamos la fórmula de la derivada del producto.

{\left[\left({t}^{2}-9\right)\left(t+4\right)\right]}^{\text{'}}={\left({t}^{2}-9\right)}^{\text{'}}\left(t+4\right)+\left({t}^{2}-9\right){\left(t+4\right)}^{\text{'}}

Resolvemos las derivadas indicadas, aplicando la propiedad de la derivada de una suma.

{\left({t}^{2}-9\right)}^{\text{'}}\left(t+4\right)+\left({t}^{2}-9\right){\left(t+4\right)}^{\text{'}}=\left(2t\right)\left(t+4\right)+\left({t}^{2}-9\right)\left(1\right)

Finalmente:

{p}^{\text{'}}\left(t\right)=2t\left(t+4\right)+{t}^{2}-9=2{t}^{2}+8t+{t}^{2}-9

{p}^{\text{'}}\left(t\right)=3{t}^{2}+8t-9

Concluimos indicando como respuesta correcta al inciso c).

Reactivo 27

Identificar la definición de derivada de h\left(x\right) .

1. {h}^{\mathrm{\text{'}}}\left(x\right)=\underset{\mathrm{\Delta }x\to 0}{lim} \frac{h\left(x+\mathrm{\Delta }x\right)-h\left(x\right)}{\mathrm{\Delta }x}
2. {h}^{\mathrm{\text{'}}}\left(x\right)=\underset{\mathrm{\Delta }x\to 0}{lim} \frac{h\left(x+\mathrm{\Delta }x\right)+h\left(x\right)}{\mathrm{\Delta }x}
3. {h}^{\mathrm{\text{'}}}\left(x\right)=\underset{x\to 0}{lim} \frac{h\left(x+\mathrm{\Delta }x\right)-h\left(x\right)}{\mathrm{\Delta }x}
4. {h}^{\mathrm{\text{'}}}\left(x\right)=\underset{\mathrm{\Delta }x\to 0}{lim} \frac{h\left(x-\mathrm{\Delta }x\right)-h\left(x\right)}{\mathrm{\Delta }x}

Solución:

Para resolver este reactivo, debes conocer los fundamentos de la derivada y su definición.

Derivada de una función:

{h}^{\mathrm{\text{'}}}\left(x\right)=\underset{\mathrm{\Delta }x\to 0}{lim} \frac{h\left(x+\mathrm{\Delta }x\right)-h\left(x\right)}{\mathrm{\Delta }x}

La respuesta correcta es el inciso a).

Reactivo 28

Calcular la derivada de la siguiente función:

y=\frac{1}{x\sqrt{4{x}^{2}-1}}

1. \frac{1-{x}^{2\sqrt{4{x}^{2}-1}}}{x}
2. \frac{1-x}{x{\left(4{x}^{2}-1\right)}^{3}}
3. \frac{1-{x}^{2}}{x{\left(4{x}^{2}-1\right)}^{2}}
4. \frac{1-8{x}^{2}}{{x}^{2}{\left(4{x}^{2}-1\right)}^{\frac{3}{2}}}

Solución:

Iniciamos aplicando la fórmula para la derivada de un cociente.

{y}^{\text{'}}=\frac{{\left(1\right)}^{\text{'}}\left(x\sqrt{4{x}^{2}-1}\right)-{\left(x\sqrt{4{x}^{2}-1}\right)}^{\text{'}}\left(1\right)}{{\left(x\sqrt{4{x}^{2}-1}\right)}^{2}}=\frac{0-{\left(x\sqrt{4{x}^{2}-1}\right)}^{\text{'}}}{{x}^{2}\left(4{x}^{2}-1\right)}=-\frac{{\left(x\sqrt{4{x}^{2}-1}\right)}^{\text{'}}}{{x}^{2}\left(4{x}^{2}-1\right)}

Aplicamos la fórmula de la derivada de un producto en la derivada del numerador.

{y}^{\text{'}}=-\frac{{\left(x\right)}^{\text{'}}\sqrt{4{x}^{2}-1}+x{\left(\sqrt{4{x}^{2}-1}\right)}^{\text{'}}}{{x}^{2}\left(4{x}^{2}-1\right)}=-\frac{\sqrt{4{x}^{2}-1}+x\frac{1}{2}{\left(4{x}^{2}-1\right)}^{-\frac{1}{2}}{\left(4{x}^{2}-1\right)}^{\text{'}}}{{x}^{2}\left(4{x}^{2}-1\right)}

{y}^{\text{'}}=-\frac{\sqrt{4{x}^{2}-1}+\frac{x}{2\sqrt{4{x}^{2}-1}}\left(8x\right)}{{x}^{2}\left(4{x}^{2}-1\right)}=-\frac{\sqrt{4{x}^{2}-1}+\frac{4{x}^{2}}{\sqrt{4{x}^{2}-1}}}{{x}^{2}\left(4{x}^{2}-1\right)}

Resolvemos la suma de fracciones.

{y}^{\text{'}}=-\frac{\sqrt{4{x}^{2}-1}+\frac{4{x}^{2}}{\sqrt{4{x}^{2}-1}}}{{x}^{2}\left(4{x}^{2}-1\right)}=-\frac{\frac{4{x}^{2}-1+4{x}^{2}}{\sqrt{4{x}^{2}-1}}}{{x}^{2}\left(4{x}^{2}-1\right)}=-\frac{8{x}^{2}-1}{{x}^{2}\left(4{x}^{2}-1\right)\sqrt{4{x}^{2}-1}}

Simplificando nos queda:

{y}^{\text{'}}=-\frac{8{x}^{2}-1}{{x}^{2}{\left(4{x}^{2}-1\right)}^{\frac{3}{2}}}=\frac{1-8{x}^{2}}{{x}^{2}{\left(4{x}^{2}-1\right)}^{\frac{3}{2}}}

Comparando con los incisos, la respuesta correcta es d).

Reactivo 29

Determinar la pendiente de la parábola y=3{x}^{2}-2x+5 en el punto x=2 .

1. 13
2. 12
3. 11
4. 10

Solución:

La derivada de una función evaluada en un punto, da como resultado la pendiente de la recta tangente en dicho punto. Teniendo en cuenta esto, para calcular la pendiente derivamos a y\left(x\right) y luego evaluamos en x=2 .

{y}^{\text{'}}=6x-2

Ahora, evaluamos en x=2 .

{y}^{\text{'}}=6\left(2\right)-2=10

La pendiente de la recta tangente a y=3{x}^{2}-2x+5 en x=2 es m=10 .

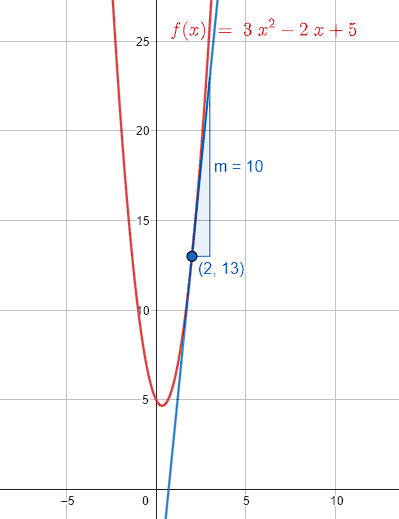
La respuesta correcta es el inciso d).

Reactivo 30

Calcular la derivada de la función

s\left(x\right)=\frac{2{e}^{x}}{{\left({e}^{x}+1\right)}^{2}}

1. -\frac{2{e}^{x}}{{\left({e}^{x}+1\right)}^{3}}
2. \frac{2{e}^{x}-1}{{\left({e}^{x}+1\right)}^{4}}
3. \frac{2{e}^{x}\left({e}^{x}-1\right)}{{\left({e}^{x}+1\right)}^{3}}
4. -\frac{2{e}^{x}\left({e}^{x}-1\right)}{{\left({e}^{x}+1\right)}^{3}}

Solución:

Iniciamos aplicando la fórmula de la derivada del cociente.

{s}^{\text{'}}\left(x\right)=\frac{{\left(2{e}^{x}\right)}^{\text{'}}\left[{\left({e}^{x}+1\right)}^{2}\right]-{\left[{\left({e}^{x}+1\right)}^{2}\right]}^{\text{'}}\left(2{e}^{x}\right)}{{\left({e}^{x}+1\right)}^{4}}

Recordemos que la derivada de {e}^{x} es {e}^{x} .

{s}^{\text{'}}\left(x\right)=\frac{2{e}^{x}\left[{\left({e}^{x}+1\right)}^{2}\right]-\left[2\left({e}^{x}+1\right)\left({e}^{x}\right)\right]\left(2{e}^{x}\right)}{{\left({e}^{x}+1\right)}^{4}}

Simplificamos.

{s}^{\text{'}}\left(x\right)=\frac{2{e}^{x}{\left({e}^{x}+1\right)}^{2}-4{e}^{2x}\left({e}^{x}+1\right)}{{\left({e}^{x}+1\right)}^{4}}=\frac{2{e}^{x}\left({e}^{x}+1\right)-4{e}^{2x}}{{\left({e}^{x}+1\right)}^{3}}

{s}^{\text{'}}\left(x\right)=\frac{2{e}^{2x}+2{e}^{x}-4{e}^{2x}}{{\left({e}^{x}+1\right)}^{3}}=\frac{2{e}^{x}-2{e}^{2x}}{{\left({e}^{x}+1\right)}^{3}}

Extraemos factor común -2{e}^{x} .

{s}^{\text{'}}\left(x\right)=-\frac{2{e}^{x}\left({e}^{x}-1\right)}{{\left({e}^{x}+1\right)}^{3}}

Concluimos que la respuesta correcta es el inciso d).