¡Felicidades aspirante! Llegamos a la cuarta y última parte de la guía resuelta de álgebra, correspondiente a los reactivos del 31 al 40, como preparación al examen de ingreso del Politécnico Nacional.

Recuerda intentar resolverlos por cuenta propia antes de consultar las respuestas, acá tienes las partes anteriores:
Reactivo 31
Realizar los siguientes productos notables:
\left(2{x}^{n+2}{z}^{1/2}-6{x}^{2m+4}+{x}^{m-2(n-1)}\right)\left(2{x}^{n+2}{z}^{1/2}+6{x}^{2m+4}+{x}^{m-2(n-1)}\right)
- 4{x}^{4}\left({x}^{2n}z+2{x}^{m-n}{z}^{1/2}+\frac{1}{4}{x}^{2m-4n}-9{x}^{4m+4}\right)
- 2{x}^{2}\left({x}^{2n}z+2{x}^{m-2n}{z}^{1/2}+{x}^{2m-4n}-9{x}^{4m+4}\right)
- 4{x}^{4}\left({x}^{2n}z+2{x}^{m-2n}{z}^{1/2}-3{x}^{2m-n}+{x}^{2m-4n}-9{x}^{4m+4}\right)
- 2{x}^{2}\left({x}^{2n}z+2{x}^{m-n}{z}^{1/2}-3{x}^{2m-n}+\frac{1}{4}{x}^{2m-4n}-9{x}^{4m+4}+2{x}^{2m-n-1}\right)
Solución:
Antes de realizar la simplificación término a término, podemos identificar que los factores son conjugados si los separamos de la siguiente forma.
\left(2{x}^{n+2}{z}^{1/2}+{x}^{m-2(n-1)}-6{x}^{2m+4}\right)\left(2{x}^{n+2}{z}^{1/2}+{x}^{m-2(n-1)}+6{x}^{2m+4}\right)
El producto de los conjugados, es igual a una diferencia de cuadrados.
{\left(2{x}^{n+2}{z}^{\frac{1}{2}}+{x}^{m-2\left(n-1\right)}\right)}^{2}-{\left(6{x}^{2m+4}\right)}^{2}={\left(2{x}^{n+2}{z}^{\frac{1}{2}}+{x}^{m-2\left(n-1\right)}\right)}^{2}-36{x}^{4m+8}
Desarrollamos el binomio al cuadrado aplicando el producto notable correspondiente.
{\left(2{x}^{n+2}{z}^{\frac{1}{2}}+{x}^{m-2\left(n-1\right)}\right)}^{2}-36{x}^{4m+8}=
={\left(2{x}^{n+2}{z}^{\frac{1}{2}}\right)}^{2}+2\left(2{x}^{n+2}{z}^{\frac{1}{2}}\right)\left({x}^{m-2\left(n-1\right)}\right)+{\left({x}^{m-2\left(n-1\right)}\right)}^{2}-36{x}^{4m+8}
Simplificamos aplicando potencia de una potencia y producto de potencias de igual base.
4{x}^{2n+4}\mathrm{z}+4{x}^{n+2+m-2\left(n-1\right)}{z}^{\frac{1}{2}}+{x}^{2m-4\left(n-1\right)}-36{x}^{4m+8}
4{x}^{2n+4}\mathrm{z}+4{x}^{m-n+4}{z}^{\frac{1}{2}}+{x}^{2m-4n+4}-36{x}^{4m+8}
Debido a que en los incisos queda un coeficiente numérico acompañando al factor común, el monomio factor común a extraer es 4{x}^{4} .
4{x}^{2n+4}\mathrm{z}+4{x}^{m-n+4}{z}^{\frac{1}{2}}+{x}^{2m-4n+4}-36{x}^{4m+8}=
=4{x}^{4}\left({x}^{2n}\mathrm{z}+{x}^{m-n}{z}^{\frac{1}{2}}+\frac{1}{4}{x}^{2m-4n}-9{x}^{4m+4}\right)
La respuesta correcta es el inciso a).
Reactivo 32
Relacionar el polinomio con su raíz.

- 1A, 2C, 3D, 4B
- 1A, 2B, 3D, 4C
- 1D, 2B, 3A, 4C
- 1D, 2C, 3A, 4B
Solución:
En este caso, debemos calcular las raíces para cada polinomio e ir relacionando los resultados parciales con la columna derecha.
Primer polinomio.
{x}^{2}+x-6=0
Podemos factorizar este polinomio encontrando a dos números que sumados sean 1 y multiplicados -6. Estas cantidades son: -2 y +3.
{x}^{2}+x-6=\left(x-2\right)\left(x+3\right)
De acá obtenemos:
{x}_{1}=2, {x}_{2}=-3
Tenemos: 1D. Descartamos los incisos c) y d).
Segundo polinomio.
{x}^{2}+4=0
Despejamos a x .
{x}^{2}=-4
Esto nos da dos raíces imaginarias conjugadas. Recordemos que la unidad imaginaria es i=\sqrt{-1} .
x=\pm 2i\to {x}_{1}=2i, {x}_{2}=-2i
Para este inciso: 2B. Con esta información: 1D, 2B, … podemos concluir que la respuesta correcta es la opción c).
Reactivo 33
Simplificar la expresión:
\left(\frac{3{x}^{3}+7{x}^{2}-40x}{{x}^{3}-2{x}^{2}-35x}\right)\left(\frac{{x}^{3}-14{x}^{2}+49x}{3{x}^{2}-8x}\right)
- \frac{1}{x+3}
- (x-7{)}^{2}
- x-7
- (x-3)(x-7)
Solución:
Iniciamos extrayendo factor común x .
\left(\frac{3{x}^{3}+7{x}^{2}-40x}{{x}^{3}-2{x}^{2}-35x}\right)\left(\frac{{x}^{3}-14{x}^{2}+49x}{3{x}^{2}-8x}\right)=\frac{x\left(3{x}^{2}+7\mathrm{x}-40\right)}{x\left({x}^{2}-2\mathrm{x}-35\right)}\cdot \frac{x\left({x}^{2}-14\mathrm{x}+49\right)}{x\left(3\mathrm{x}-8\right)}
=\frac{3{x}^{2}+7\mathrm{x}-40}{{x}^{2}-2\mathrm{x}-35}\cdot \frac{{x}^{2}-14\mathrm{x}+49}{3\mathrm{x}-8}
Ahora, factorizamos a los polinomios {x}^{2}-14\mathrm{x}+49 y {x}^{2}-2\mathrm{x}-35 .
{x}^{2}-14\mathrm{x}+49=\left(x-7\right)\left(x-7\right)={\left(x-7\right)}^{2}
{x}^{2}-2\mathrm{x}-35=\left(x-7\right)\left(x+5\right)
Sustituimos.
\frac{3{x}^{2}+7\mathrm{x}-40}{{x}^{2}-2\mathrm{x}-35}\cdot \frac{{x}^{2}-14\mathrm{x}+49}{3\mathrm{x}-8}=\frac{3{x}^{2}+7\mathrm{x}-40}{\left(x-7\right)\left(x+5\right)}\cdot \frac{{\left(x-7\right)}^{2}}{3\mathrm{x}-8}=\frac{3{x}^{2}+7\mathrm{x}-40}{x+5}\cdot \frac{\left(x-7\right)}{3\mathrm{x}-8}
Al polinomio 3{x}^{2}+7\mathrm{x}-40 lo factorizamos aplicando la fórmula de segundo grado.
3{x}^{2}+7\mathrm{x}-40=\left(x+5\right)\left(3x-8\right)
\frac{3{x}^{2}+7\mathrm{x}-40}{x+5}\cdot \frac{\left(x-7\right)}{3\mathrm{x}-8}=\frac{\left(x+5\right)\left(3x-8\right)}{x+5}\cdot \frac{\left(x-7\right)}{3\mathrm{x}-8}
Simplificamos.
\frac{\left(x+5\right)\left(3x-8\right)}{x+5}\cdot \frac{\left(x-7\right)}{3\mathrm{x}-8}=x-7
Finalmente:
\left(\frac{3{x}^{3}+7{x}^{2}-40x}{{x}^{3}-2{x}^{2}-35x}\right)\left(\frac{{x}^{3}-14{x}^{2}+49x}{3{x}^{2}-8x}\right)=x-7
La respuesta correcta es el inciso c).
¿Conoces cuántos puntos necesitas para quedar? Conoce los aciertos por carrera del IPN.
Reactivo 34
Obtener el resultado de la siguiente división de polinomios:
\frac{8{x}^{4}+44{x}^{3}+30{x}^{2}-175x-250}{x-2}
- 8{x}^{3}+60{x}^{2}+150x+125
- 8{x}^{3}+60{x}^{2}-150x+125
- 8{x}^{3}-60{x}^{2}+150x-25
- 8{x}^{3}-60{x}^{2}-150x-25
Solución:
Para resolver el cociente entre los polinomios, aplicamos el algoritmo de la división sintética o el método de Ruffini. En esta ocasión, emplearemos el algoritmo de la división sintética.
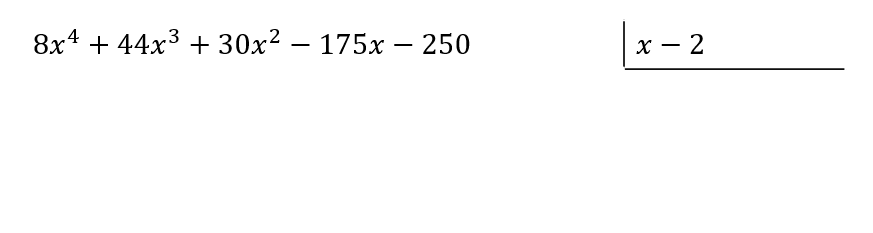
Recordemos que el cociente se obtiene dividiendo el término de mayor grado del dividendo con el término de mayor grado del divisor. Para 8{x}^{4} , el monomio que se debe multiplicar por x es 8{x}^{3} .
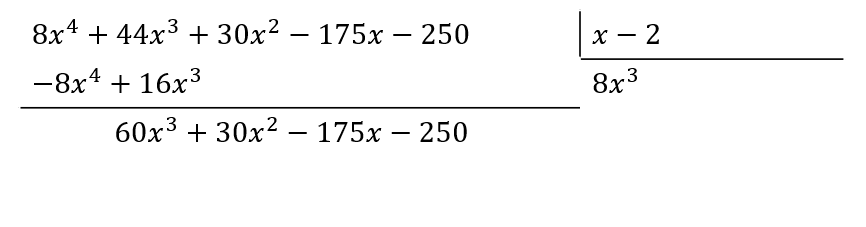
El siguiente término del cociente debe ser 60{x}^{2} .
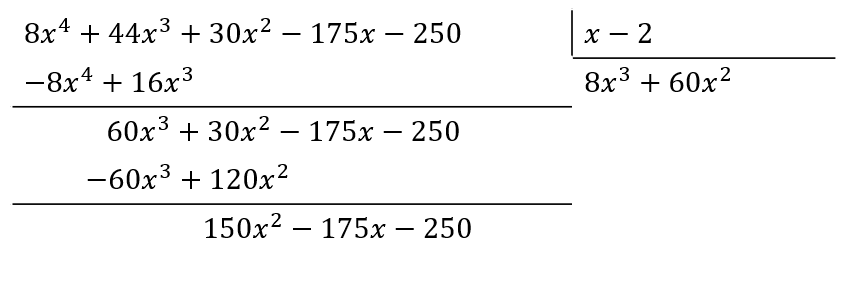
Con este resultado parcial descartamos a los incisos c y d. El siguiente término del cociente es +150x .
Con esto no es necesario continuar con la división, sabemos que el cociente hasta este punto es 8{x}^{3}+60{x}^{2}+150x+\dots esta información es suficiente para concluir que la respuesta correcta es el inciso a).
Reactivo 35
Determinar los valores de las constantes A, B, y C para que la igualdad de polinomios sea válida.
2A{x}^{2}+Ax+C=-5{x}^{2}+(2B+1)x+3
- A=-7/2,B=-5/4,C=3
- A=-5/2,B=-7/4,C=3
- A=-7/4,B=-5/2,C=-3
- A=-5/4,B=-7/2,C=-3
Solución:
Para que dos polinomios sean iguales, sus coeficientes deben ser iguales.
\begin{array}{c}2A=-5\\ A=2B+1\\ C=3\end{array}
Del sistema de ecuaciones anterior, podemos conocer de forma directa los valores de A y C :
A=-\frac{5}{2}, C=3
Esta información es suficiente para concluir que la respuesta correcta es el inciso b).
Reactivo 36
Evaluar la función:
{S}_{n}\left(x\right)=(-1{)}^{2n+1}{2}^{n}{\left(\frac{{A}^{2}}{4}\right)}^{3/2}\mathrm{s}\mathrm{e}\mathrm{n}\left[\frac{(2n+1)}{2}\pi x\right]
En x=1,x=2,x=3 , para valores de n=0 .
- {S}_{0}\left(1\right)=-2{\left(\frac{A}{2}\right)}^{3/2},{S}_{0}\left(2\right)=0,{S}_{0}\left(3\right)={\left(\frac{A}{2}\right)}^{3}
- {S}_{0}\left(1\right)={\left(\frac{A}{2}\right)}^{3},{S}_{0}\left(2\right)=0,{S}_{0}\left(3\right)=-{\left(\frac{A}{2}\right)}^{3}
- {S}_{0}\left(1\right)=0,{S}_{0}\left(2\right)=-2{\left(\frac{A}{2}\right)}^{3/2},{S}_{0}\left(3\right)={\left(\frac{A}{2}\right)}^{3}
- {S}_{0}\left(1\right)=-{\left(\frac{A}{2}\right)}^{3},{S}_{0}\left(2\right)=0,{S}_{0}\left(3\right)={\left(\frac{A}{2}\right)}^{3}
Solución:
Primero sustituimos el valor de n en la expresión.
{S}_{0}\left(x\right)=(-1{)}^{1}{2}^{0}{\left(\frac{{A}^{2}}{4}\right)}^{\frac{3}{2}}\mathrm{sen}\left[\frac{\left(1\right)}{2}\pi x\right]=-{\left(\frac{{A}^{2}}{4}\right)}^{\frac{3}{2}}\mathrm{sen}\left[\frac{1}{2}\pi x\right]=-{\left(\frac{\mathrm{A}}{2}\right)}^{3}\mathrm{sen}\left[\frac{1}{2}\pi x\right]
Evaluamos x=1 .
{S}_{0}\left(x=1\right)=-{\left(\frac{\mathrm{A}}{2}\right)}^{3}\mathrm{sen}\left[\frac{1}{2}\pi \left(1\right)\right]=-{\left(\frac{\mathrm{A}}{2}\right)}^{3}\mathrm{sen}\left(\frac{\pi }{2}\right)
El seno de pi medios es igual a +1.
{S}_{0}\left(x=1\right)=-{\left(\frac{\mathrm{A}}{2}\right)}^{3}
El único inciso que tiene este resultado para {S}_{0}\left(x=1\right) es el d). Concluimos que la respuesta correcta es la opción d).
Reactivo 37
Identificar la solución que corresponde al sistema de ecuaciones.
\begin{array}{c}-x-2y=-3\\ -4x-5y=-6\end{array}
- x=6,y=-3/2
- x=2,y=1/2
- x=2,y=-1
- x=-1,y=2
Solución:
Para resolver el sistema de ecuaciones podemos emplear el método de preferencia: sustitución, igualación, reducción o Cramer. Esta vez, aplicaremos el método por reducción. Iniciamos multiplicando la primera ecuación por -4.
\begin{array}{c}-x-2y=-3\\ -4x-5y=-6\end{array}\to \begin{array}{c}4x+8y=12\\ -4x-5y=-6\end{array}
Sumando las ecuaciones nos queda:
3y=6\to y=2
No es necesario continuar resolviendo. El inciso d) es el único con y=2 . El inciso d) es la respuesta correcta.
Reactivo 38
Identificar las ecuaciones que tienen por solución:
x=3/4,y=-7/4
- 2x-2y=5,-3x+y=-4
- x-2y=3,-2x+y=4
- x-5y=\mathrm{2,3}x-y=-4
- x-3y=2,-x+5y=-4
Solución:
Para comprobar qué sistema de ecuaciones viene representado por los valores de x y y , sustituimos los valores en ambas ecuaciones, si se cumple la igualdad en ambas ese par de coordenadas es la solución del sistema.
Sistema de ecuaciones del inciso a.
2x-2y=5,-3x+y=-4
2\left(\frac{3}{4}\right)-2\left(-\frac{7}{4}\right)=5,-3\left(\frac{3}{4}\right)-\frac{7}{4}=-4
\frac{3}{2}+\frac{7}{2}=5,-\frac{9}{4}-\frac{7}{4}=-4
\therefore 5=5, -4=-4
El sistema de ecuaciones del inciso a) cumple la igualdad. Indicamos a la opción a) como la respuesta correcta.
Reactivo 39
Una empresa textil le vende a una tienda del sur 1200 playeras (P1) y 700 pantalones (P2) por $66, 000.00, mientras que a la tienda del norte le envía 2000 playeras y 1500 pantalones por un monto de $130 000.00. ¿Cuál es el costo unitario para P1 y P2 que maneja la empresa?
- P1=10,P2=30
- P1=25,P2=40
- P1=20,P2=60
- P1=45,P2=30
Solución:
Iniciamos expresando las relaciones entre playeras y pantalones como expresiones matemáticas.
1200{P}_{1}+700{P}_{2}=66000
2000{P}_{1}+1500{P}_{2}=130000
Dividimos ambas ecuaciones por 100.
12{P}_{1}+7{P}_{2}=660
20{P}_{1}+15{P}_{2}=1300
A la segunda ecuación la podemos simplificar nuevamente dividiéndola por 5.
12{P}_{1}+7{P}_{2}=660
4{P}_{1}+3{P}_{2}=260
Multiplicamos a la segunda ecuación por -3.
12{P}_{1}+7{P}_{2}=660
-12{P}_{1}-9{P}_{2}=-780
Sumamos las ecuaciones:
-2{P}_{2}=-120\to {P}_{2}=60
El único inciso con {P}_{2}=60 es el c).
P1=20,P2=60
La respuesta correcta es la opción c).
Reactivo 40
Identificar el polinomio de raíces reales que reproduce la siguiente gráfica:
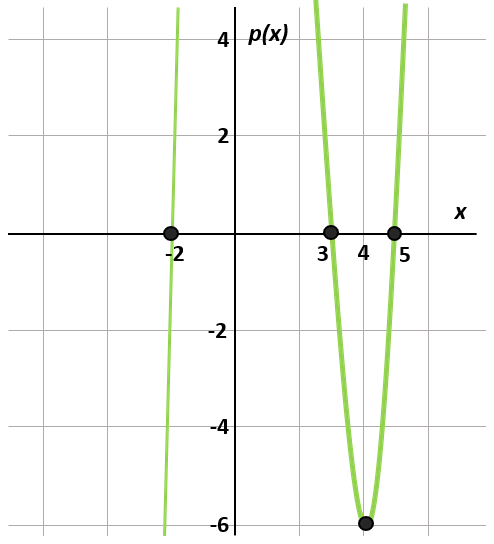
- {x}^{3}-4{x}^{2}-3x+18
- {x}^{3}-6{x}^{2}-x+30
- {x}^{3}-4{x}^{2}-3x-18
- {x}^{3}-3{x}^{2}-x+30
Solución:
Las raíces del polinomio, según el gráfico, deberán ser:
{x}_{1}=-2, {x}_{2}=3, {x}_{3}=5
Expresadas como producto, nos queda:
\left(x+2\right)\left(x-3\right)\left(x-5\right)=0
Desarrollamos.
\left({x}^{2}-3x+2x-6\right)\left(x-5\right)=0\to \left({x}^{2}-x-6\right)\left(x-5\right)=0
{x}^{3}-{x}^{2}-6x-5{x}^{2}+5x+30=0
Simplificamos.
{x}^{3}-6{x}^{2}-x+30=0
El polinomio p\left(x\right) es igual a {x}^{3}-6{x}^{2}-x+30 .
La respuesta correcta es el inciso b).


