¿Problemas resolviendo la guía de álgebra IPN 2023? No te preocupes, ¡llegaste al lugar correcto! En este tutorial vamos a resolver los primeros 10 reactivos de álgebra de la guía de ingreso al Instituto Politécnico Nacional.

Te dejo un resumen con los puntos clave de la convocatoria IPN 2023.
- Carreras ofertadas en IPN: 70+.
- Porcentaje de Aceptación: 20%.
- Preguntas en el examen de Admisión: 140 preguntas.
- Nuevos temas: historia e inglés (reading comprehension).
- Tipo: selección múltiple.
Estructura del Examen IPN
En la nueva estructura, la cantidad de reactivos por asignatura cambia según el área de conocimientos de tu carrera. Te recuerdo que las carreras en el Politécnico Nacional se dividen en 3 áreas:
- Ingeniería y Ciencias Físico Matemáticas IyCFM
- Ciencias Sociales y Administrativas CSA
- Ciencias Médico Biológias CMB
La siguiente tabla muestra la estructura de reactivos por materia para cada área.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
¿Qué tan difícil es el examen al IPN?
Es una pregunta recurrente entre los aspirantes, pero sí: es muy difícil. Si no comienzas a estudiar a tiempo, si no fortaleces tus debilidades, si no aceleras tu capacidad de análisis frente a los problemas; el examen te parecerá difícil.
Para la convocatoria de este año se han agregado 2 asignaturas nuevas y la estructura ha cambiado. En la guía de álgebra los reactivos tienen una complejidad aumentada respecto a los años anteriores.
Temario álgebra IPN
Estos son los temas de álgebra que deberás dominar antes de presentar el examen de ingreso:
- Números reales
- Propiedades
- Operaciones básicas
- Proporciones
- Expresiones algebraicas
- Lenguaje algebraico
- Expresiones fraccionarias
- Leyes de los exponentes y los radicales
- Productos notables
- Métodos de factorización
- Funciones y ecuaciones lineales
- Concepto de función
- Propiedades de las desigualdades
- Ecuaciones lineales
- Sistemas de ecuaciones lineales
- Funciones y ecuaciones cuadráticas
- Concepto de función cuadrática
- Ecuaciones cuadráticas
¿Cómo resolver la guía del IPN?
Inicia examinando la bibliografía recomendada por el IPN. Estudia el temario y comprende los fundamentos. Un error común entre los aspirantes consiste en leer los temas mientras resuelven la guía.
Los siguientes hacks te ayudarán a mejorar el desempeño, resolviendo la mayor cantidad de reactivos en el menor tiempo y así obtener los aciertos necesarios para quedar en tu carrera.
- Resuelve cada parte por tu cuenta antes de checar las respuestas. Utiliza este material a modo de consulta.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
- Te advierto que la guía del IPN 2023 tiene algunos errores, aquí te señalamos cuáles son.
Reactivo 1
El conjunto de números ___________ y __________ constituye a los números ________.
- irracionales – racionales – trascendentes
- irracionales – reales – racionales
- irracionales – reales – trascendentes
- irracionales – racionales – reales
Solución:
Para encontrar el enunciado que contiene los conceptos que completan correctamente a la frase, debemos recordar cuál es la estructura de los conjuntos numéricos.
Iniciamos con los números naturales N , compuestos por todos los números positivos sin decimales incluido el cero.
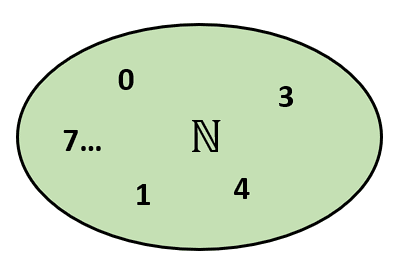
A partir de este conjunto, se construyen los enteros \mathbb{Z} , compuesto por todos los números sin decimales positivos y negativos, incluido el cero.
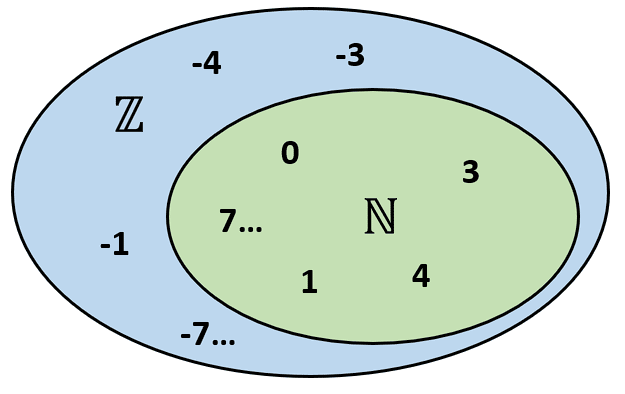
Teniendo a todos los enteros, se construye el conjunto de los racionales \mathbb{Q} . Son todos aquellos números que pueden expresarse como el cociente entre dos enteros. Este conjunto es la extensión de los enteros.
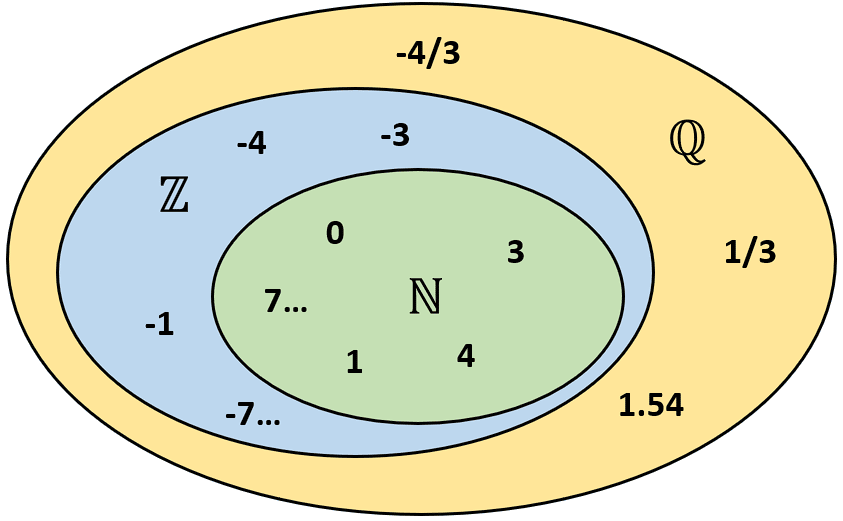
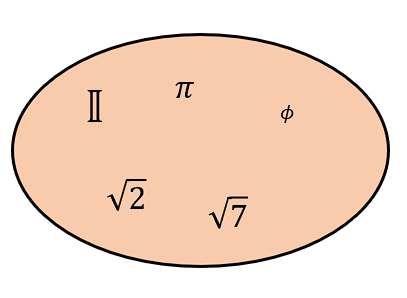
El siguiente conjunto numérico es el de los irracionales \mathbb{I} . Estos números son la contraparte de los racionales (de ahí su nombre), debido a que no se pueden expresar como el cociente de dos enteros.
Son cantidades con decimales infinitos no periódicos. Se representan como un conjunto aparte de los racionales. Por otro lado, los irracionales se subdividen en: trascendentes y algebraicos.
La unión de estos dos grandes conjuntos: irracionales y racionales, forman a los números reales
\mathbb{R} .
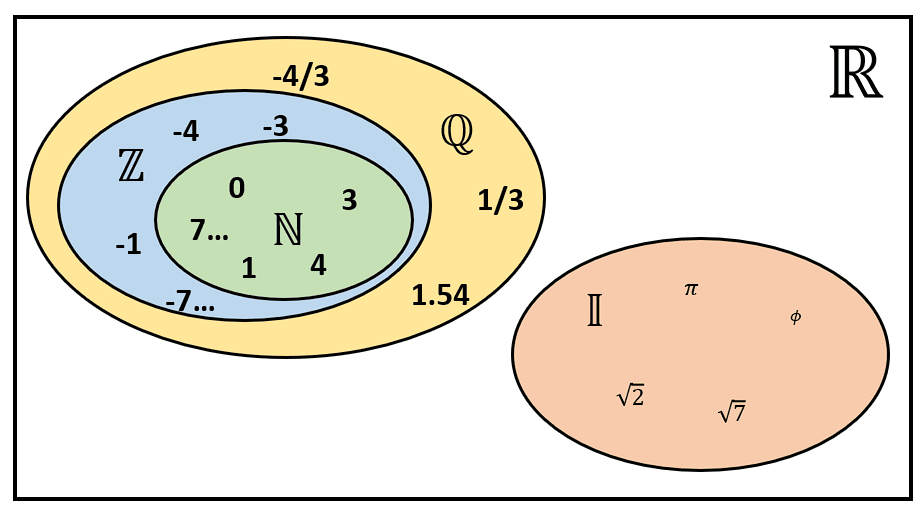
Teniendo en cuenta todo lo anterior y examinando los incisos, concluimos que el d) completa de forma correcta a la frase del enunciado.
El conjunto de números irracionales y racionales constituye a los números reales.
La solución parece extensa porque acá te mencionamos los fundamentos detrás de la respuesta correcta. Toda la justificación se fundamenta en los temas de conjuntos numéricos.
Reactivo 2
La propiedad de _________ hace válida la igualdad:
\frac{10}{\sqrt{5}}=2\sqrt{5}
- inverso aditivo
- inverso multiplicativo
- elemento neutro aditivo
- elemento neutro multiplicativo
Solución:
Debemos iniciar reconociendo la operación que permite llevar a la expresión \frac{10}{\sqrt{5}} hacia 2\sqrt{5} . En este caso, se está aplicando una racionalización del denominador de la fracción.
Debido a que el radical es un monomio con índice 2, el artificio matemático que se emplea es el de multiplicar y dividir por el mismo radical.
\frac{10}{\sqrt{5}}=\frac{10}{\sqrt{5}}\cdot 1=\frac{10}{\sqrt{5}}\cdot \frac{\sqrt{5}}{\sqrt{5}}=\frac{10\sqrt{5}}{{\left(\sqrt{5}\right)}^{2}}=\frac{10\sqrt{5}}{5}=2\sqrt{5}
El segundo paso del artificio, indica que se multiplica por 1, resultado que se obtiene al dividir un número sobre sí mismo, por ejemplo \frac{\sqrt{5}}{\sqrt{5}} . Desde el punto de vista de las propiedades de la multiplicación, el 1 corresponde al elemento neutro de la multiplicación.
La propiedad de elemento neutro multiplicativo hace válida la igualdad…
Concluimos indicando como respuesta correcta al inciso d).
Reactivo 3
Relacionar la igualdad con su propiedad.
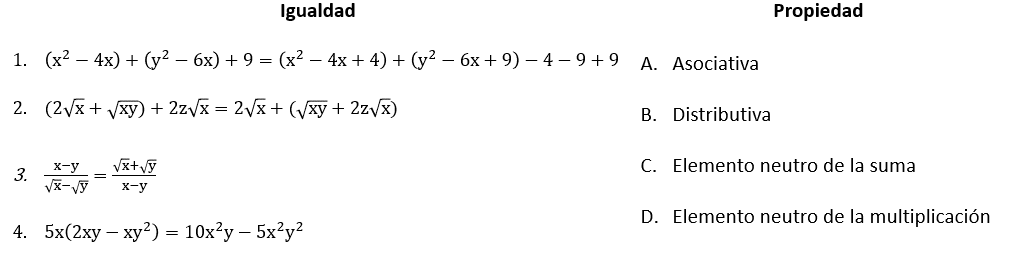
- 1C, 2A, 3D, 4B
- 1D, 2B, 3C, 4A
- 1A, 2C, 3B, 4D
- 1B, 2C, 3A, 4D
Solución:
En este caso, vamos a analizar las operaciones empleadas en los incisos de la columna izquierda, para relacionarlos con la propiedad correspondiente a la derecha.
Igualdad del inciso 1.
\left({x}^{2}-4x\right)+\left({y}^{2}-6x\right)+9=\left({x}^{2}-4x+4\right)+\left({y}^{2}-6x+9\right)-4-9+9
Para llevar a la expresión de la derecha, se debe sumar 4 y 9 dentro de los paréntesis respectivamente y a restarlos fuera de los paréntesis. Esto es equivalente a sumar cero dos veces.
\left({x}^{2}-4x+4\right)+\left({y}^{2}-6x+9\right)-4-9+9={x}^{2}-4x+4+{y}^{2}-6x+9-4-9+9
{x}^{2}-4x+4+{y}^{2}-6x+9-4-9+9=\left({x}^{2}-4x\right)+\left({y}^{2}-6x\right)-4+4-9+9+9
\left({x}^{2}-4x\right)+\left({y}^{2}-6x\right)-4+4-9+9+9=\left({x}^{2}-4x\right)+\left({y}^{2}-6x\right)+9
La propiedad empleada en este caso es la del elemento neutro de la suma. 1C. Examinando los incisos, solo el A inicia por 1C. Por lo tanto, con la información que tenemos podemos concluir que la respuesta correcta es el inciso a).
Reactivo 4
¿Qué opción ordena de menor a mayor el siguiente conjunto de números?
\left\{2\sqrt{2},\frac{2}{\sqrt{2}},\mathrm{2,1},\sqrt[5]{2}\right\}
- \left\{\mathrm{1,2},\frac{2}{\sqrt{2}},\sqrt[5]{2},2\sqrt{2}\right\}
- \left\{\mathrm{1,2},\sqrt[5]{2},2\sqrt{2},\frac{2}{\sqrt{2}}\right\}
- \left\{1,\frac{2}{\sqrt{2}},\mathrm{2,2}\sqrt{2},\sqrt[5]{2}\right\}
- \left\{1,\sqrt[5]{2},\frac{2}{\sqrt{2}},\mathrm{2,2}\sqrt{2}\right\}
Solución:
Antes de iniciar la solución, vamos a racionalizar el término \frac{2}{\sqrt{2}} .
\left\{2\sqrt{2},\frac{2}{\sqrt{2}},\mathrm{2,1},\sqrt[5]{2}\right\}\to \left\{2\sqrt{2},\sqrt{2},\mathrm{2,1},\sqrt[5]{2}\right\}
Ahora, la raíz cuadrada de 2 es aproximadamente 1.414 . Ahora, la raíz quinta de 2 debe ser un número menor que \sqrt{2} pero mayor que 1.
1<\sqrt[5]{2}<\sqrt{2}
Con seguridad sabemos que el 1 es el menor y le sigue \sqrt[5]{2} según el análisis anterior. Solo el inciso d) inicia 1, \sqrt[5]{2}, \dots Concluimos entonces que la respuesta correcta es el inciso d).
Reactivo 5
Simplificar la expresión:
\frac{\sqrt{\left({x}^{2}+6x+9\right)(x+2)}\cdot \sqrt{{x}^{2}-x-6}}{\sqrt{{x}^{2}-9}\cdot (x+2)}
- \sqrt{x-3}
- \sqrt{x+3}
- \frac{\sqrt{x-3}}{x+2}
- \sqrt{x-3}\cdot \left(x+2\right)
Solución:
Para simplificar la expresión del enunciado, debemos factorizar a las expresiones de segundo grado que se encuentran en el numerador y el denominador. Iniciamos con el trinomio {x}^{2}+6x+9 .
Buscamos dos números que sumados sean +6 y multiplicados +9.
\frac{\sqrt{\left({x}^{2}+6x+9\right)(x+2)}\cdot \sqrt{{x}^{2}-x-6}}{\sqrt{{x}^{2}-9}\cdot (x+2)}=\frac{\sqrt{\left(x+3\right)\left(x+3\right)(x+2)}\cdot \sqrt{{x}^{2}-x-6}}{\sqrt{{x}^{2}-9}\cdot (x+2)}
\frac{\sqrt{\left(x+3\right)\left(x+3\right)\left(x+2\right)}\cdot \sqrt{{x}^{2}-x-6}}{\sqrt{{x}^{2}-9}\cdot \left(x+2\right)}=\frac{\sqrt{{\left(x+3\right)}^{2}\left(x+2\right)}\cdot \sqrt{{x}^{2}-x-6}}{\sqrt{{x}^{2}-9}\cdot \left(x+2\right)}
=\frac{(x+3)\sqrt{(x+2)}\cdot \sqrt{{x}^{2}-x-6}}{\sqrt{{x}^{2}-9}\cdot (x+2)}
Ahora vamos con el trinomio {x}^{2}-x-6 . Dos números que sumados sean -1 y multiplicados -6.
{x}^{2}-x-6=\left(x-3\right)\left(x+2\right)
\frac{(x+3)\sqrt{(x+2)}\cdot \sqrt{{x}^{2}-x-6}}{\sqrt{{x}^{2}-9}\cdot (x+2)}=\frac{(x+3)\sqrt{(x+2)}\cdot \sqrt{\left(x-3\right)\left(x+2\right)}}{\sqrt{{x}^{2}-9}\cdot (x+2)}
\frac{(x+3)\sqrt{(x+2)}\cdot \sqrt{\left(x-3\right)\left(x+2\right)}}{\sqrt{{x}^{2}-9}\cdot (x+2)}=\frac{(x+3)\sqrt{(x+2)}\sqrt{\left(x-3\right)}\sqrt{\left(x+2\right)}}{\sqrt{{x}^{2}-9}\cdot (x+2)}
\frac{(x+3)\sqrt{(x+2)}\sqrt{\left(x-3\right)}\sqrt{\left(x+2\right)}}{\sqrt{{x}^{2}-9}\cdot (x+2)}=\frac{(x+3)(x+2)\sqrt{\left(x-3\right)}}{\sqrt{{x}^{2}-9}\cdot (x+2)}
Finalmente, al denominador lo factorizamos aplicando diferencia de cuadrados.
\frac{(x+3)(x+2)\sqrt{\left(x-3\right)}}{\sqrt{{x}^{2}-9}\cdot (x+2)}=\frac{(x+3)(x+2)\sqrt{\left(x-3\right)}}{\sqrt{\left(x+3\right)\left(x-3\right)}\cdot (x+2)}=\frac{(x+3)(x+2)\sqrt{\left(x-3\right)}}{\sqrt{\left(x+3\right)}\sqrt{\left(x-3\right)}(x+2)}
Simplificamos.
\frac{(x+3)(x+2)\sqrt{\left(x-3\right)}}{\sqrt{\left(x+3\right)}\sqrt{\left(x-3\right)}(x+2)}=\frac{(x+3)(x+2)}{\sqrt{\left(x+3\right)}(x+2)}=\frac{(x+3)}{\sqrt{\left(x+3\right)}}
Finalmente:
\frac{(x+3)}{\sqrt{\left(x+3\right)}}=\left(x+3\right){\left(x+3\right)}^{-1/2}=\sqrt{x+3}
\therefore \frac{\sqrt{\left({x}^{2}+6x+9\right)(x+2)}\cdot \sqrt{{x}^{2}-x-6}}{\sqrt{{x}^{2}-9}\cdot (x+2)}=\sqrt{x+3}
Concluimos indicando como respuesta correcta al inciso b).
Reactivo 6
En la expresión, calcular el valor de x .
\frac{1/2}{6x-1}=\frac{2}{8x-3}
- 1/3
- 3/4
- 1/16
- 3/32
Solución:
Despejamos los denominadores en ambas fracciones.
\frac{1/2}{6x-1}=\frac{2}{8x-3}\to \frac{1}{2}\left(8x-3\right)=2\left(6x-1\right)
Simplificamos.
\frac{1}{2}\left(8x-3\right)=2\left(6x-1\right)\to 8x-3=4\left(6x-1\right)\to 8x-3=24x-4
Despejamos a la variable x .
8x-3=24x-4\to 8x-24x=-4+3
-16x=-1
\therefore x=\frac{1}{16}
Indicamos como respuesta correcta al inciso c).
Reactivo 7
Resolver el siguiente producto:
\sqrt{17+2\sqrt{30}}\sqrt{17-2\sqrt{30}}
- \sqrt{34}
- \sqrt{77}
- 13
- 17
Solución:
Debido a que las raíces tienen el mismo índice, podemos unir el producto dentro de un mismo radical.
\sqrt{17+2\sqrt{30}}\sqrt{17-2\sqrt{30}}=\sqrt{\left(17+2\sqrt{30}\right)\cdot \left(17-2\sqrt{30}\right)}
El producto es el de binomios conjugados. Por lo tanto, podemos evitar el desarrollo y emplear el producto notable correspondiente.
\left(a+b\right)\left(a-b\right)={a}^{2}-{b}^{2}
\sqrt{\left(17+2\sqrt{30}\right)\cdot \left(17-2\sqrt{30}\right)}=\sqrt{{17}^{2}-{\left(2\sqrt{30}\right)}^{2}}=\sqrt{{17}^{2}-4\left(30\right)}=\sqrt{{17}^{2}-120}
Sustituimos el resultado de la potencia {17}^{2}=289 .
\sqrt{{17}^{2}-120}=\sqrt{289-120}=\sqrt{169}
La raíz cuadrada de 169 es 13.
\sqrt{169}=13
La respuesta correcta es el inciso c). Si no tienes calculadora, una forma de concluir la respuesta es calcular el cuadrado de los números sin raíces en los enunciados, es decir, del 13 y 17.
Reactivo 8
Evaluar las funciones:
h\left(x\right)={x}^{3}-2x-3 y s\left(x\right)=\frac{2}{3}{x}^{2}+4x
Para calcular la diferencia:
s\left(3\right)-2h\left(2\right)=
- 20
- 16
- 4
- 8
Solución:
Este problema consiste en evaluar las funciones y calcular el resultado indicado en el enunciado. Iniciamos por obtener la imagen para h\left(x\right) y s\left(x\right) .
h\left(x=2\right)={2}^{3}-2\left(2\right)-3=8-4-3=1
s\left(x=3\right)=\frac{2}{3}{\left(3\right)}^{2}+4\left(3\right)=6+12=18
Sustituimos en la expresión:
s\left(3\right)-2h\left(2\right)=18-2\left(1\right)=18-2=16
La respuesta correcta al problema es el inciso b).
Reactivo 9
Relacionar la fracción con su representación en decimales periódicos.

- 1A, 2D, 3C, 4B
- 1A, 2C, 3D, 4B
- 1B, 2D, 3C, 4A
- 1B, 2C, 3D, 4A
Solución:
En lugar de resolver cada una de las fracciones de la izquierda para relacionarla con los decimales periódicos de la derecha, vamos a analizar ciertas características que nos permitan reducir la cantidad de pasos.
Las únicas fracciones que pueden arrojar decimales con una parte entera mayor que cero, son la 1 y la 4. Ambas fracciones tienen como denominador el 9, por lo tanto, el resultado del cociente depende de qué tan grande sea el numerador.
El 4 tiene como numerador 17 y el inciso uno al 13. Como resultado parcial: 1B y 4A. Los únicos incisos con estas opciones son el c) y el d). Solo debemos resolver una división para determinar cuál de los dos incisos es el correcto.
La fracción \frac{1}{3} es un número racional bastante conocido, cuyo resultado es 0.333\dots Por lo tanto: 3D. Esta información es suficiente para concluir que el pareo correcto es: 1B, 2C, 3D, 4A. Concluimos indicando como respuesta correcta al inciso d).
Reactivo 10
Una fábrica de zapatos tiene un supervisor por cada 25 empleados. Para mejorar la calidad del trabajo, los directivos decidieron asignar un supervisor por cada 15 empleados. Si, actualmente, hay 300 empleados, ¿cuántos supervisores más será necesario contratar?
- 9
- 8
- 7
- 6
Solución:
Inicialmente, la empresa tiene una razón de supervisores por empleados de:
\frac{1}{25}\cdot \frac{\mathrm{s}\mathrm{u}\mathrm{p}}{\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{o}\mathrm{s}}
Si multiplicamos esta razón por los 300 empleados nos quedan:
{s}_{1}=\frac{1}{25}\cdot \frac{\mathrm{s}\mathrm{u}\mathrm{p}}{\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{o}\mathrm{s}}\cdot 300 \mathrm{e}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{o}\mathrm{s}=12\mathrm{ }\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}
La razón de supervisores cambia a:
\frac{1}{15}\cdot \frac{\mathrm{s}\mathrm{u}\mathrm{p}}{\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{o}\mathrm{s}}
Multiplicamos nuevamente por los 300 empleados.
{s}_{2}=\frac{1}{15}\cdot \frac{\mathrm{s}\mathrm{u}\mathrm{p}}{\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{o}\mathrm{s}}\cdot 300 \mathrm{e}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{o}\mathrm{s}=20\mathrm{ }\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}
Si la empresa inicialmente tenía 12 supervisores, debe contratar a 8 para cumplir con el nuevo requerimiento. La respuesta correcta es el inciso b).

