Llegamos a la quinta y última parte del simulacro de física para el área de Ciencias Médico Biológicas del Instituto Politécnico Nacional.

¡Felicidades por llegar a esta última parte! Recuerda continuar tu ruta de estudio en las demás materias de conocimientos generales utilizando todas las herramientas que colocamos a tu disposición.
Reactivo 41
A partir del circuito eléctrico que se muestra en la figura, calcule la corriente que circula a través de la resistencia {R}_{3} .
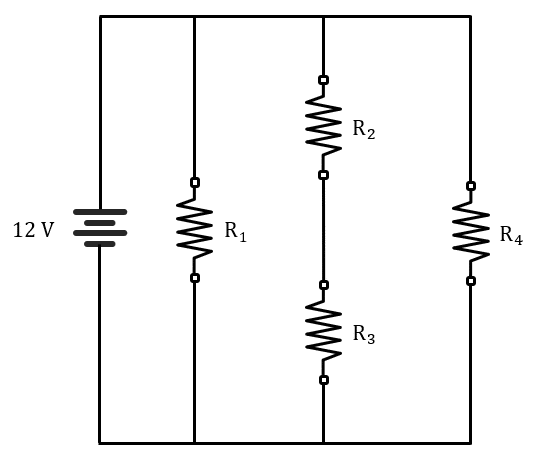
Tenga en cuenta que: {R}_{1}={R}_{2}={R}_{3}={R}_{4}=1 \mathrm{\Omega } .
- 6 A
- 9 A
- 12 A
- 30 A
Solución:
Aunque el circuito parezca complejo, podemos analizar su topología para buscar un voltaje o una corriente que simplifique el cálculo solicitado por el enunciado. Lo primero que vemos es que la pila de 12 volts está en paralelo a {R}_{1} , a la serie {R}_{2} {R}_{3} y a la resistencia {R}_{4} .
Esto simplifica mucho el cálculo, ya que solo nos interesa la corriente que circula a través de {R}_{3} , que es la misma que circula a través de {R}_{2} por encontrarse en serie. Ya que los 12 volts caen entre los terminales de la serie, podemos calcular la {i}_{23} como:
12 \mathrm{V}=\left({R}_{2}+{R}_{3}\right){i}_{23}
Recordemos que resistencias en serie se suman. Despejamos a {i}_{23} y sustituimos.
{i}_{23}=\frac{12 \mathrm{V}}{1\mathrm{\Omega }+1\mathrm{\Omega }}=6 \mathrm{A}
La corriente que circula a través de la resistencia {R}_{3} es de 6 amperios.
Examinando los incisos, concluimos que la respuesta correcta está en el a).
Reactivo 42
A partir de un experimento, se ha encontrado que la fuerza de repulsión entre dos cargas eléctricas es de 40 N cuando están a una distancia {d}_{1} . ¿Cuál sería la magnitud de la fuerza si las cargas se sitúan a 1/3 de la distancia original?
- 180 N
- 200 N
- 300 N
- 360 N
Solución:
Para resolver este problema debemos utilizar la Ley de Coulomb, de tal forma que haciendo el cociente entre las fuerzas podamos eliminar el resto de variables que no conocemos como la magnitud de las cargas.
Para el primer momento del experimento, la fuerza eléctrica es:
{F}_{1}=\frac{{k}_{e}{q}_{1}{q}_{2}}{{d}_{1}^{2}}
Ahora, luego de acortar la distancia a {d}_{2}=\frac{{d}_{1}}{3} obtenemos:
{F}_{2}=\frac{{k}_{e}{q}_{1}{q}_{2}}{{d}_{2}^{2}}=\frac{{k}_{e}{q}_{1}{q}_{2}}{{\left(\frac{{d}_{1}}{3}\right)}^{2}}=9\frac{{k}_{e}{q}_{1}{q}_{2}}{{d}_{1}^{2}}
Dividimos ambas fuerzas:
\frac{{F}_{1}}{{F}_{2}}=\frac{\frac{{k}_{e}{q}_{1}{q}_{2}}{{d}_{1}^{2}}}{9\frac{{k}_{e}{q}_{1}{q}_{2}}{{d}_{1}^{2}}}=\frac{1}{9}
Despejamos la fuerza 2.
{F}_{2}=9{F}_{1}
Sustituimos {F}_{1}=40 \mathrm{N} .
{F}_{2}=360 \mathrm{N}
La fuerza ha aumentado 9 veces al disminuir la distancia a una tercera parte.
Concluimos que la respuesta correcta es el inciso d).
Reactivo 43
Relacione correctamente el concepto en la columna izquierda con su respectiva formulación matemática en la columna derecha.

- 1A, 2C, 3D, 4B
- 1B, 2D, 3C, 4A
- 1B, 2C, 3A, 4D
- 1B, 2C, 3D, 4A
Solución:
Para relacionar cada uno de los conceptos con las ecuaciones de la columna derecha, analizaremos paso a paso cada una de las leyes.
Ley de Faraday.
Establece que la fuerza electromotriz inducida en un circuito es directamente proporcional al número de espiras y a la variación de flujo magnético respecto del tiempo.
\epsilon =N\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}=N\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}
Para este inciso: 1B.
Ley de Ohm.
Esta ley es fundamental en el análisis de circuitos eléctricos, pues establece que la relación entre la caída de tensión V en un resistor es linealmente proporcional a la corriente I que lo circula, a través de un factor constante R llamado resistencia eléctrica.
V=R\cdot I
Para este inciso: 2C.
Fuerza magnética sobre una carga.
Establece que una carga eléctrica q que se desplaza a lo largo de un campo magnético de intensidad B , a una rapidez v , experimenta sobre ella una fuerza magnética perpendicular al plano del campo y el desplazamiento.
F=qvB
Para este inciso: 3D.
Flujo magnético.
Esta cantidad escalar nos permite cuantificar la cantidad de líneas de campo magnético B a través de una superficie con área A .
\mathrm{\Phi }=B\cdot A
Para este inciso: 4A.
Uniendo todas las soluciones, obtenemos que: 1B, 2C, 3D, 4A.
Comparando con los incisos, concluimos que la respuesta correcta se encuentra en el d).
Reactivo 44
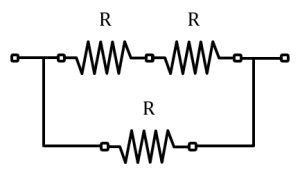
Identifique cuál de las siguientes configuraciones posee mayor resistencia eléctrica. Tenga en cuenta que R=1 \mathrm{\Omega } .
Solución:
Para resolver este problema, vamos a ir encontrando la resistencia equivalente de cada inciso, de tal forma que la mayor será la respuesta al ejercicio.
Arreglo A.
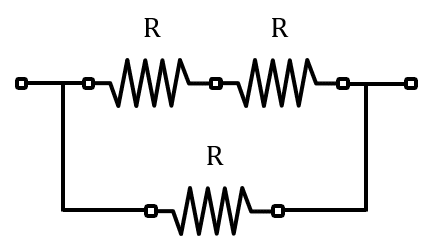
La resistencia equivalente es igual al paralelo de la serie R+R y R .
{R}_{A}=\frac{2{R}^{2}}{2R+R}=\frac{2}{3}R
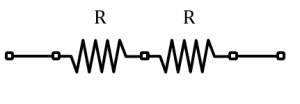
Arreglo B.
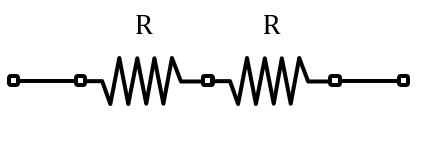
La resistencia equivalente es igual a la suma de los resistores R .
{R}_{B}=2R
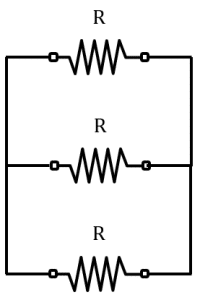
Arreglo C.
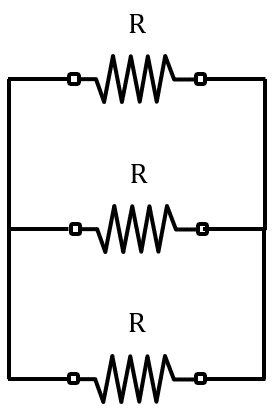
Es el paralelo de 3 resistencias R .
{R}_{B}=\frac{1}{\frac{1}{R}+\frac{1}{R}+\frac{1}{R}}=\frac{R}{3}
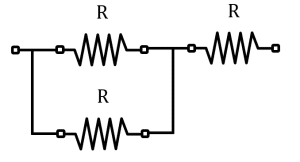
Arreglo D.
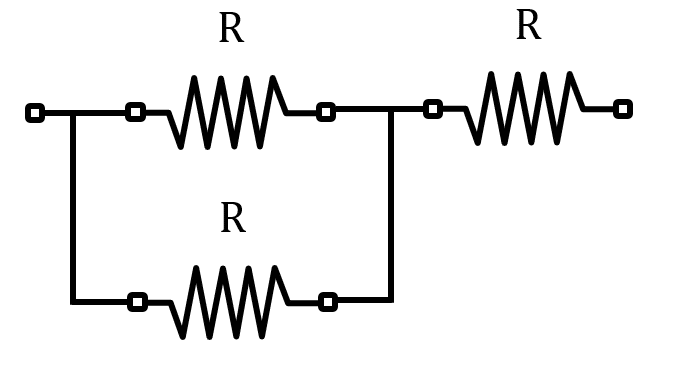
Este arreglo es la serie de un paralelo y R.
{R}_{D}=\frac{{R}^{2}}{R+R}+R=\frac{R}{2}+R=\frac{3}{2}R
Comparando los resultados, concluimos que el arreglo con la mayor resistencia es el b).
Reactivo 45
A partir del electroimán conectado a la pila que se muestra en la figura, indique el sentido de las líneas de campo para la configuración mostrada.
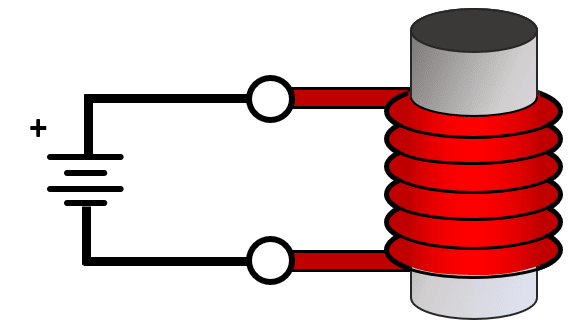
- Norte a Sur
- Sur a Sur
- Sur a Norte
- Norte a Norte
Solución:
Desde los experimentos de Oersted, sabemos que al hacer circular una corriente eléctrica a través de un hilo conductor, alrededor de éste se forma un campo magnético circular y centrado en el alambre conductor.
Más tarde, se descubrió que al enrollar alambre alrededor de un material ferromagnético (aquellos que favorecen el flujo magnético) se consigue construir un imán artificial, también conocidos como electroimanes.
Para conocer el sentido de las líneas de campo eléctrico, utilizamos la regla de la mano derecha. Colocamos los dedos apuntando en la dirección de la corriente y hacia donde termine apuntando el pulgar, hacia allí salen las líneas de campo.
Debido a que el terminal positivo de la pila se encuentra conectado en la parte superior del electroimán, siguiendo el sentido del cable encontramos que el campo magnético apunta hacia abajo.
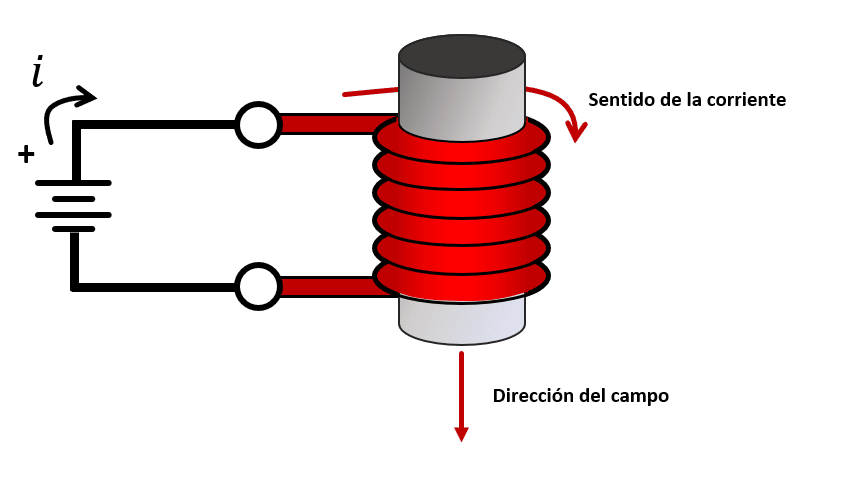
Las líneas de campo magnético apuntan de Norte a Sur.
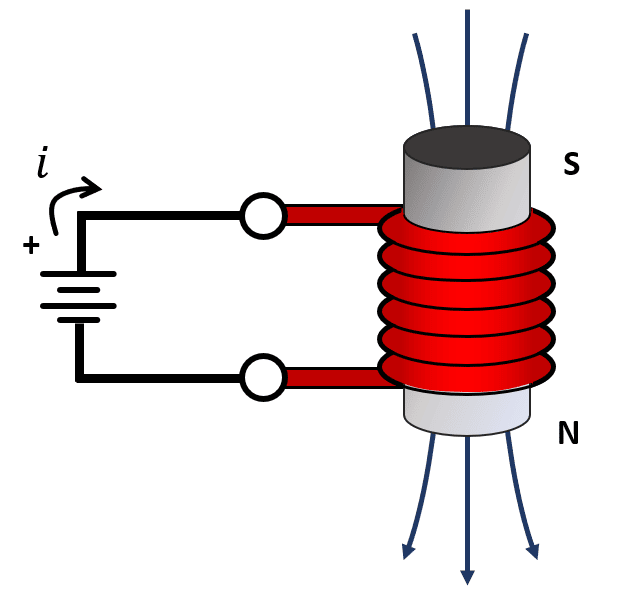
Comparando con los incisos, concluimos que la respuesta correcta es el a).
Reactivo 46
Calcule el índice de refracción que experimenta un rayo de luz que va desde el medio A hacia el medio B, teniendo en cuenta que sus índices de refracción absolutos son 1.36 y 4.22 respectivamente.
- 0.133
- 0.322
- 3.1
- 4.22
Solución:
En este caso, debemos calcular el índice de retracción relativo {n}_{\mathrm{A}-\mathrm{B}} que se obtiene como el cociente entre el índice absoluto {n}_{A} respecto al índice relativo {n}_{B} .
{n}_{A-B}=\frac{{n}_{A}}{{n}_{B}}
Sustituimos los valores dados:
{n}_{A-B}=\frac{1.36}{4.22}=0.322
Concluimos que la respuesta correcta es el inciso b).
Reactivo 47
Calcule la potencia de consumo de una estufa eléctrica conectada a una red de 110 V y que presenta una resistencia eléctrica de 100 \mathrm{\Omega } .
- 50 W
- 88 W
- 100 W
- 121 W
Solución:
La potencia eléctrica es aquella que consumen los elementos resistivos en un circuito eléctrico cuando por ellos circula una corriente. Dicha potencia que disipa en forma de calor se puede calcular con cualquiera de las siguientes expresiones, equivalentes todas gracias a la Ley de Ohm.
P=V\cdot I=\frac{{V}^{2}}{R}=R\cdot {I}^{2}
En nuestro caso, tenemos como dato al voltaje V=110 \mathrm{V} y a la resistencia eléctrica R=100 \mathrm{\Omega } .
P=\frac{{\left(110\right)}^{2}}{100}=121 \mathrm{w}
La estufa consume 121 watts de potencia.
La respuesta correcta es el inciso d).
Reactivo 48
La principal característica de las lentes convergentes es que…
- Son más gruesas en los extremos y estrechas en el centro
- Son más gruesas en el centro y estrechas en los extremos
- Tienen forma de prisma curvo
- Siempre producen imágenes virtuales
Solución:
Como sabemos, una lente es todo medio transparente que se encuentra limitado por dos caras, donde al menos una de ellas es curva. Las lentes más comunes en óptica son las denominadas esféricas, debido a que sus caras corresponden a superficies esféricas.
Entre ellas, se clasifican de dos formas: convergentes y divergentes. La principal diferencia entre ellas es su construcción geométrica, las convergentes poseen caras convexas y las divergentes cóncavas.
Teniendo esto en cuenta y examinando las opciones, concluimos que la respuesta correcta es el b).
Reactivo 49
Cuando dos ondas electromagnéticas viajan en el vacío y se encuentran en un punto, de tal forma que se anulan mutuamente, esto se denomina…
- Efecto Doppler
- Dualidad onda partícula
- Interferencia constructiva
- Interferencia destructiva
Solución:
Debido a que la radiación electromagnética puede estudiarse de forma clásica a través de los fenómenos ondulatorios, cuando dos o más ondas electromagnéticas se encuentran en un punto se interfieren unas a otras, de tal forma que el resultado puede ser una onda con mayor o menor amplitud que las originales.
En el caso que la resultante tenga amplitud nula, se dice que la interferencia es destructiva, en caso contrario que la amplitud sea la suma de las ondas originales, entonces se trata de interferencia constructiva.
Teniendo en cuenta esto y considerando los incisos, concluimos que la respuesta correcta es el d).
Reactivo 50
Calcule la frecuencia de una onda electromagnética cuya longitud de onda es de 20 nm y viaja a 3\cdot {10}^{8} \mathrm{m}/\mathrm{s} .
- 1.5\cdot {10}^{16} \mathrm{H}\mathrm{z}
- 1.5\cdot {10}^{15} \mathrm{H}\mathrm{z}
- 1.5\cdot {10}^{17} \mathrm{H}\mathrm{z}
- 15\cdot {10}^{16} \mathrm{H}\mathrm{z}
Solución:
Recordemos la relación que existe entre la frecuencia, la velocidad y la longitud de una onda:
v=\lambda \cdot f
De esta podemos despejar directamente la frecuencia:
f=\frac{v}{\lambda }
Recordemos que nanómetros es {10}^{-9} , por tanto:
f=\frac{3\cdot {10}^{8} \mathrm{m}/\mathrm{s}}{20\cdot {10}^{-9} \mathrm{m}}=1.5\cdot {10}^{16} \mathrm{H}\mathrm{z}
La onda tiene una frecuencia de 15 peta Hertz.
Concluimos que la respuesta correcta es el inciso a).