Seguimos con la segunda para del simulacro de Geometría y trigonometría, vamos a resolver los ejercicios del 11 al 20, recuerda tomar apuntes como si estuvieras haciendo el examen real.

Reactivo 11
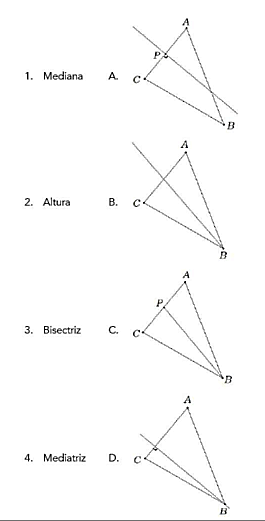
Relacionar la recta notable del triángulo con su respectiva figura.
- 1B, 2D, 3C, 4A
- 1C, 2D, 3B, 4A
- 1B, 2A, 3C, 4D
- 1C, 2A, 3B, 4D
Solución:
Para resolver este problema, es necesario aplicar algo de teoría sobre las rectas notables en el triángulo. Comenzaremos por examinar la recta en cada triángulo de la columna derecha, identificar su clasificación y luego emparejarla con una de las opciones en la columna izquierda.
Triángulo A
La recta que corta a este triángulo tiene la particularidad de que intersecta al lado \overline{C A} perpendicularmente en el punto P . Además, dicho punto P es también el punto medio del lado \overline{C A} .
Esta descripción encaja con la definición de mediatriz. De esta manera, concluimos que la recta A es la mediatriz del triángulo, por tanto: 4A.
Triángulo B
Esta recta pasa por el vértice B , cortando además a la mitad el ángulo que se forma en dicho vértice del triángulo. La recta notable conocida por dividir a la mitad cualquiera de los 3 ángulos de un triángulo, se denomina bisectriz.
Concluimos entonces que la recta B es una bisectriz del triángulo, por tanto: 3B.
Triángulo C
El segmento de recta de este triángulo, tiene uno de sus extremos en el vértice B y el otro en el punto medio del lado \overline{C A} , que es paralelo a dicho vértice. La recta notable que cumple con esta descripción es la mediana.
Concluimos entonces que la recta C es una mediana del triángulo, por tanto: 1C.
Triángulo D
Por simple completación, esta recta debería ser una de las alturas del triángulo, pero vale la pena analizar el porqué de dicha afirmación.
En principio, la recta es perpendicular al lado \overline{C A} del triángulo y pasa por el vértice que es paralelo a ese lado, es decir, el vértice B . La recta notable que, en efecto, cumple con esa descripción es la altura.
Concluimos entonces que la recta D es una de las alturas del triángulo, por tanto: 2D.
Uniendo todas las soluciones en orden numérico creciente nos queda que: 1C, 2D, 3B, 4A. Comparando con las opciones que ofrece el problema, la correcta es la b).
Reactivo 12
La intersección de las __________ de un triángulo se conoce como circuncentro.
- Alturas
- Medianas
- Bisectrices
- Mediatrices
Solución:
Según la teoría de puntos notables en un triángulo, el circuncentro es el punto en el que se intersectan las mediatrices de un triángulo. La mediatriz es una recta que corta el punto medio de uno de los lados y es también perpendicular a él.
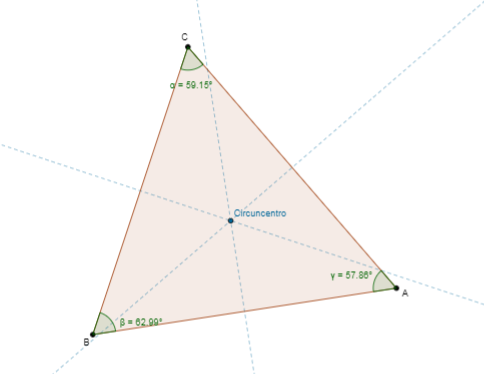
Concluimos entonces que la respuesta correcta es la d) Mediatrices. Se le llama circuncentro, porque dicho punto es el centro de una circunferencia que pasa por los tres vértices del triángulo.
La intersección de las Mediatrices de un triángulo se conoce como circuncentro.
Reactivo 13
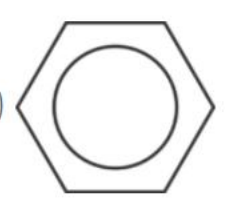
¿Qué figura representa una circunferencia inscrita en un hexágono?
Solución:
Según la teoría de polígonos regulares, a una circunferencia se le llama inscrita cuando se encuentra dentro del polígono y es también tangente a todos sus lados en un punto.
A partir de la definición anterior, queda claro que las opciones a) y b) no pueden ser correctas. En la primera, es la circunferencia quien contiene al hexágono y en la segunda, la circunferencia pasa por los vértices del hexágono, característica que corresponde a la circunferencia exinscrita.
La opción c) es la correcta. Se encuentra interna al hexágono y es tangente en un punto a sus lados. Por su parte, la opción d) no es correcta. Es interior pero no tangente a los lados.
Concluimos finalmente que la respuesta correcta es la c).

Circunferencia inscrita en un hexágono.
Reactivo 14
Un ángulo mide 2 x+20 y su ángulo opuesto por el vértice mide 5 x-34 . Encontrar la medida de cada ángulo.
- 18°
- 34°
- 56°
- 72°
Solución:
En este problema aplicaremos las relaciones existentes entre ángulos opuestos por el vértice.
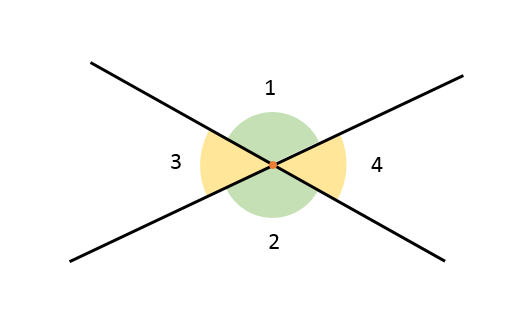
Podemos escoger cualquier par de ángulos. Esta vez serán 3 y 4. La relación dice que 3 y 4 deben ser iguales si son opuestos por el vértice. Es decir, 2 x+20 debe ser igual a 5 x-34 .
5 x-34=2 x+20
Despejamos a x de la ecuación:
5 x-2 x=20+34 \rightarrow 3 x=54
\therefore x=18^{\circ}
Sustituimos este valor en cualquiera de las ecuaciones para encontrar el valor que deben tener ambos ángulos.
\alpha=5 x-34=5\left(18^{\circ}\right)-34=56^{\circ}
Concluimos entonces que la respuesta correcta es la c).
Una persona mide 1.80 m y proyecta una sombra de 60 cm. Si a la misma hora la sombra de un árbol es de 3 m ¿Cuántos metros mide el árbol?
- 6
- 8
- 9
- 11
Solución:
El análisis es similar al problema anterior. Ambas sombras forman un ángulo de 90° con los objetos que la proyectan, en este caso el árbol y la persona, generando así dos triángulos rectángulos semejantes donde la incógnita es la altura del árbol. Aplicamos la propiedad de proporción entre los lados de los triángulos.
\frac{h_{a}}{h_{p}}=\frac{S_{a}}{S_{p}}
Despejamos de esta relación la altura del árbol h_{a} :
h_{a}=S_{a} \frac{h_{p}}{S_{p}}=(3 m) \frac{1.8 m}{0.6 m}=9 m
Concluimos entonces que la respuesta correcta es la c), el árbol mide 9 metros de altura.
Reactivo 16
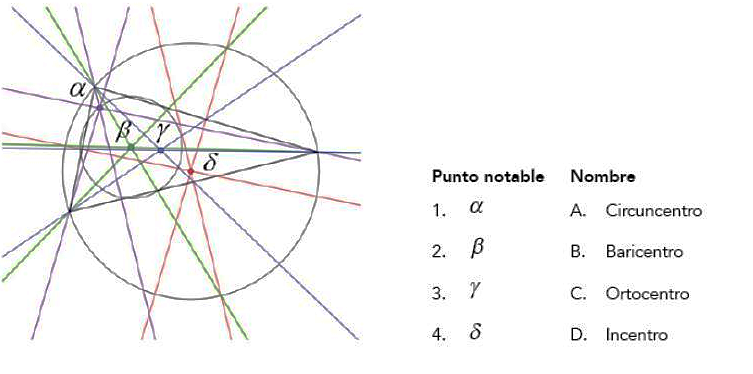
Asociar los puntos notables trazados en el triángulo con el nombre que corresponde a cada uno:
- 1C, 2D, 3A, 4B
- 1C, 2D, 3B, 4A
- 1A, 2B, 3D, 4C
- 1A, 2B, 3C, 4D
Solución:
Para resolver este problema, analizaremos la situación de cada uno de los puntos en la columna izquierda para luego asociarlo con la denominación correcta en la columna derecha.
Punto notable \alpha
Es el punto de intersección de las rectas en color morado. Inspeccionándolas nos daremos cuenta de que son las alturas del triángulo. Por definición, el punto notable que tiene como intersección las alturas de un triángulo se denomina ortocentro.
Concluimos entonces que 1C.
Punto notable \beta
Este punto es la intersección de las rectas de color verde. Las tres rectas parecen cortar a la mitad el ángulo formado en el vértice por el que pasan. Esta descripción concuerda con la de las bisectrices y su punto notable de intersección es el incentro.
Concluimos entonces que 2D.
Punto notable \gamma
Por este punto pasan las tres rectas en color azul. En este caso, tienen la particularidad de pasar por un vértice y el punto medio del lado paralelo a dicho vértice. La recta notable que cumple con esa descripción es la mediana, cuyo punto de intersección se llama baricentro.
Concluimos entonces que 3B.
Punto notable \delta
Es el último punto de la lista y por el que pasan las rectas de color rojo. Dichas rectas son perpendiculares a los lados en sus respectivos puntos medios. Reciben el nombre de mediatrices y su intersección se conoce como circuncentro.
Concluimos entonces que 4A.
Uniendo todas las soluciones, nos queda 1C, 2D, 3B, 4A correspondiente con la opción b).
Reactivo 17
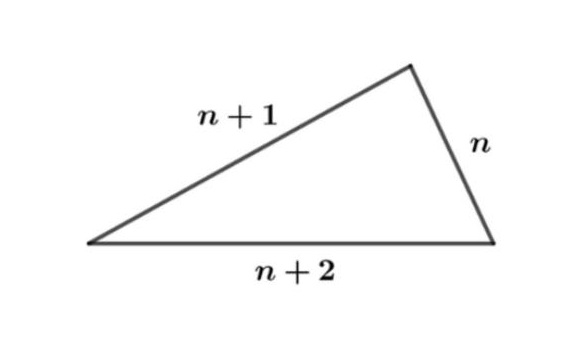
Calcular el valor del entero n en el siguiente triángulo si su perímetro es igual a 24.
- 5
- 7
- 9
- 11
Solución:
El perímetro de cualquier figura geométrica se entiende como la magnitud (lo que mide) de todo su trazo. El trazo de un cuadrado son sus 4 lados, el de un pentágono los 5 lados y el de una circunferencia, la línea curva cerrada alrededor del centro.
Para un triángulo como es el caso, será la suma de sus tres lados, igualado a 24, tal como lo indica el enunciado.
(n+1)+(n)+(n+2)=24
Resolvemos sumas y despejamos el valor de n .
3 n+3=24 \rightarrow 3 n=21
\therefore n=7
Concluimos entonces que la respuesta correcta es la b).
Reactivo 18
Se necesita medir la altura de un edificio de 8 pisos, desafortunadamente solo contamos con una cinta métrica de 5m, lo cual hace poco práctico medir la altura con dicha cinta. Para medir la altura del edificio procederemos como sigue: a cierta hora del día el edificio proyecta sobre el suelo una sombra que al medirla con nuestra cinta nos da 20 m. Al siguiente día a la misma hora mido la altura que proyecta mi cuerpo, que es de 90 cm. Si mi altura es de 1.8 m, la altura del edificio es:
- 46 m
- 42 m
- 40 m
- 36 m
Solución:
Para analizar este problema, será útil hacer un bosquejo de cómo se ha proyectado la sombra del edificio y de la persona que hace la medición:

Ya que ambas mediciones se han realizado a la misma hora del día, se garantiza que el ángulo al que el sol proyecta las sombras es el mismo, por lo tanto, si unimos los extremos libres en ambas situaciones obtendremos dos triángulos rectángulos semejantes.
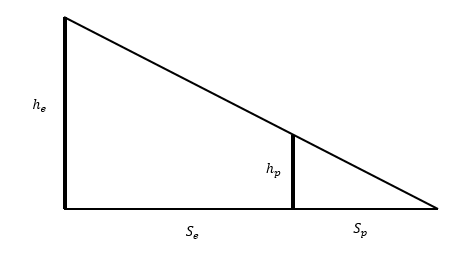
Es necesario aclarar que los triángulos están dispuestos en la posición de Thales para triángulos semejantes. Es decir, los vértices de la derecha de ambas figuras están superpuestos. Aplicamos entonces la proporcionalidad entre los lados:
\frac{h_{e}}{h_{p}}=\frac{S_{e}}{S_{p}}
Despejamos la altura del edificio h_{e} :
h_{e}=S_{e} \frac{h_{p}}{S_{p}}
h_{e}=(20 \mathrm{~m}) \frac{1.8 \mathrm{~m}}{0.9 \mathrm{~m}}=40 \mathrm{~m}
La respuesta correcta al problema es la c), el edificio tiene 40 metros de altura.
Reactivo 19
Encontrar la altura del edificio, si se sitúa a un punto de 20 metros, además de que su ángulo de elevación al punto más alto es de 45°.
- 20 m
- 25 m
- 30 m
- 35 m
Solución:
Para analizar este problema, es necesario hacer un bosquejo de la situación planteada.
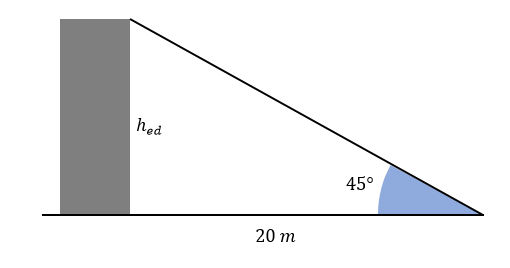
Vemos como se forma un triángulo rectángulo, donde: el cateto adyacente es la distancia de 20 metros y el cateto opuesto la altura del edificio que se desea calcular. Todo eso respecto al ángulo de 45° formado con la horizontal, también llamado ángulo de elevación en el enunciado.
Necesitamos una identidad trigonométrica que relacione los catetos de un triángulo respecto a uno de los ángulos. La tangente es esa identidad:
\tan 45^{\circ}=\frac{C O}{C A}
El cateto opuesto al ángulo es h_{e d} y el adyacente la distancia de 20 metros. Sustituimos y despejamos el valor de h_{e d} .
\tan 45^{\circ}=\frac{h_{e d}}{20} \rightarrow h_{e d}=20 \tan 45^{\circ}
La tangente de 45° es 1:
h_{e d}=20 \tan 45^{\circ}=20 m
Concluimos entonces que la altura del edificio es de 20 metros. La respuesta correcta es la a).
Reactivo 20
Calcular la longitud del segmento \overline{D E} en el siguiente triángulo si se conoce que |\overline{A B}|=10 \mathrm{~cm} , 3|\overline{D C}|=|\overline{A C}| \text { y } \overline{D E} / / \overline{A B} .
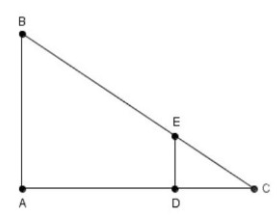
- 20/30
- 10/3
- 10/6
- 3/10
Solución:
Lo primero que identificamos es que ambos son triángulos rectángulos semejantes. Además, el problema nos da la proporción entre los lados |\overline{D C}| \text { у }|\overline{A C}| , donde |\overline{A C}| pertenece al triángulo A B C y el lado |\overline{D C}| al triángulo C D E .
3|\overline{D C}|=|\overline{A C}|
Que podemos escribir como:
\frac{|\overline{A C}|}{|\overline{D C}|}=3
Aplicando ahora la propiedad de proporcionalidad entre los lados de dos triángulos semejantes, sabemos que:
\frac{|\overline{A B}|}{|\overline{D E}|}=\frac{|\overline{A C}|}{|\overline{D C}|}=3
Ya que \overline{D E} / / \overline{A B} (las dos barras inclinadas quieren decir paralelo a)
Como el problema nos da el valor del lado |\overline{A B}| , podemos emplear la proporción para calcular el segmento solicitado \overline{D E} :
\frac{|\overline{A B}|}{|\overline{D E}|}=3 \rightarrow|\overline{D E}|=\frac{|\overline{A B}|}{3}
\therefore \overline{D E}=\frac{10}{3} \mathrm{~cm}
Concluimos que la respuesta correcta es la b).