Guía IPN 2023 resuelta Álgebra – ejercicios del 21 al 30 – Parte 3

Vamos a resolver la tercera parte de la guía de álgebra del IPN 2023. En este tutorial, continuamos con la solución paso a paso de los reactivos desde el 21 al 30.

¡Algunos reactivos de la guía tienen errores! A lo largo del post te indicamos cuáles son, mientras revisamos algunos hacks para que no cometas los mismos errores en el examen.

Reactivo 21

Simplificar la siguiente expresión:

\frac{{x}^{8}{y}^{4}{z}^{-8}}{{x}^{-3}{y}^{3}{z}^{-2}}

1. {x}^{11}y{z}^{-10}
2. {x}^{5}y{z}^{-6}
3. {x}^{11}y{z}^{-6}
4. {x}^{5}{y}^{7}{z}^{-10}

Solución:

Este problema es bastante sencillo, solo debemos aplicar la propiedad del cociente de potencias de igual base. Recordando la propiedad:

\frac{{a}^{n}}{{a}^{m}}={a}^{n-m}

Aplicando esto a la fracción del enunciado nos queda:

\frac{{x}^{8}{y}^{4}{z}^{-8}}{{x}^{-3}{y}^{3}{z}^{-2}}={x}^{8-\left(-3\right)}{y}^{4-3}{z}^{-8-\left(-2\right)}={x}^{8+3}{y}^{1}{z}^{-8+2}={x}^{11}{y}^{1}{z}^{-6}

Finalmente:

\frac{{x}^{8}{y}^{4}{z}^{-8}}{{x}^{-3}{y}^{3}{z}^{-2}}={x}^{11}\cdot y\cdot {z}^{-6}

Comparando con los incisos, concluimos que la respuesta correcta se encuentra en c).

Reactivo 22

Ordenar la secuencia de pasos a seguir para racionalizar el denominador de la expresión \frac{{x}^{2}-81}{\sqrt{x}-3} .

1. \frac{{x}^{2}-81}{\sqrt{x}-3}
2. (x+9)(\sqrt{x}+3)
3. \frac{(x-9)(x+9)(\sqrt{x}+3)}{x-9}
4. \frac{(x-9)(x+9)(\sqrt{x}+3)}{(\sqrt{x}-3)(\sqrt{x}+3)}
5. \left(\frac{(x-9)(x+9)}{\sqrt{x}-3}\right)\left(\frac{\sqrt{x}+3}{\sqrt{x}+3}\right)

 

1. 3, 1, 2, 4, 5
2. 1, 5, 4, 3, 2
3. 1, 5, 3, 2, 4
4. 3, 2, 1, 4, 5

Solución:

Para racionalizar una fracción cuyo denominador es un binomio con radicales, aplicamos el artificio matemático de multiplicar y dividir por su conjugado.

Además, sabemos que partimos de la expresión en sí: \frac{{x}^{2}-81}{\sqrt{x}-3} , por lo que el primer paso es el 1. Con esto descartamos a los incisos a y d. El siguiente paso sería el 5, porque se multiplica y divide por el conjugado de \sqrt{x}-3 , es decir: \sqrt{x}+3 .

Debido a que es el producto entre dos fracciones, se realiza una multiplicación lineal. Esto se lleva a cabo en el paso 4. Con esta información: 1, 5, 4, … tenemos suficiente para concluir que la respuesta correcta es el inciso b).

Reactivo 23

Simplificar la expresión:

\left(\frac{\sqrt[3]{x}-3}{\sqrt[3]{x}+3}\right)\cdot \left(\frac{\sqrt[3]{{x}^{2}}+3\sqrt[3]{x}+9}{\sqrt[3]{{x}^{2}}-3\sqrt[3]{x}+9}\right)\cdot \left(\frac{3x+81}{x-27}\right)

1. 1
2. 2
3. 3
4. 4

Solución:

Para resolver este problema, debemos aplicar la factorización para una diferencia de cubos.

{a}^{3}\pm {b}^{3}=\left(a\pm b\right)\left({a}^{2}\mp ab+{b}^{2}\right)

Tenemos que identificar tanto en el numerador como en el denominador cuál es el binomio que debemos factorizar. Esto lo hacemos elevando al cuadrado a los términos del binomio, si dan como resultado \sqrt[3]{{x}^{2}} y 9 respectivamente.

Debido a la similitud, podemos intuir que dichos binomios son \sqrt[3]{x}-3 y \sqrt[3]{x}+3 . Ahora, extraemos factor común 3 de 3x+81 .

\left(\frac{\sqrt[3]{x}-3}{\sqrt[3]{x}+3}\right)\cdot \left(\frac{\sqrt[3]{{x}^{2}}+3\sqrt[3]{x}+9}{\sqrt[3]{{x}^{2}}-3\sqrt[3]{x}+9}\right)\cdot \left(\frac{3x+81}{x-27}\right)=3\left(\frac{\sqrt[3]{x}-3}{\sqrt[3]{x}+3}\right)\cdot \left(\frac{\sqrt[3]{{x}^{2}}+3\sqrt[3]{x}+9}{\sqrt[3]{{x}^{2}}-3\sqrt[3]{x}+9}\right)\cdot \left(\frac{x+27}{x-27}\right)

La factorización de \sqrt[3]{x}-3 es:

\sqrt[3]{x}-3=\left(x-27\right)\left(\sqrt[3]{{x}^{2}}-3\sqrt[3]{x}+9\right)

Mientras que la factorización de \sqrt[3]{x}+3 es:

\sqrt[3]{x}+3=\left(x+27\right)\left(\sqrt[3]{{x}^{2}}+3\sqrt[3]{x}+9\right)

Sustituimos estas igualdades en la expresión.

3\left(\frac{\sqrt[3]{x}-3}{\sqrt[3]{x}+3}\right)\cdot \frac{\left(x+27\right)\left(\sqrt[3]{{x}^{2}}+3\sqrt[3]{x}+9\right)}{\left(x-27\right)\left(\sqrt[3]{{x}^{2}}-3\sqrt[3]{x}+9\right)}=3\left(\frac{\sqrt[3]{x}-3}{\sqrt[3]{x}+3}\right)\cdot \frac{\sqrt[3]{x}+3}{\sqrt[3]{x}-3}=3

Finalmente:

\left(\frac{\sqrt[3]{x}-3}{\sqrt[3]{x}+3}\right)\cdot \left(\frac{\sqrt[3]{{x}^{2}}+3\sqrt[3]{x}+9}{\sqrt[3]{{x}^{2}}-3\sqrt[3]{x}+9}\right)\cdot \left(\frac{3x+81}{x-27}\right)=3

Comparando con los incisos, indicamos como respuesta correcta al c).

Reactivo 24

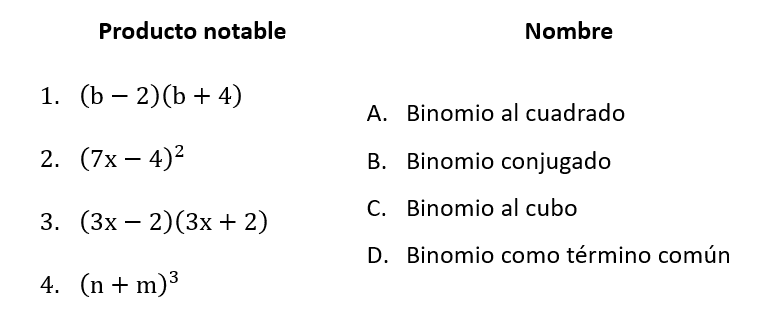
Relacionar el producto notable con su nombre.

1. 1A, 2B, 3C, 4D
2. 1B, 2C, 3D, 4A
3. 1D, 2A, 3B, 4C
4. 1D, 2B, 3A, 4C

Solución:

Vamos a ir examinando a las expresiones algebraicas en la columna izquierda, para relacionarla con su correspondiente propiedad indicada en la columna derecha.

En el producto del inciso 1, no se identifica ningún producto notable. Para llegar hacia esta factorización, se aplicó factor común sobre alguno de los binomios, por lo tanto: 1D. Descartamos al inciso a) y al b).

Ahora, la expresión del inciso 2 muestra a un binomio elevado al cuadrado. Comparando con los nombres en la columna derecha: 2A. Con esta información: 1D, 2A, … tenemos suficiente información para concluir que la respuesta correcta es la opción c).

Reactivo 25

Desarrollar el producto:

{\left({x}^{2n+1}{y}^{2}-\frac{1}{3}{x}^{2}{y}^{2n-1}\right)}^{2}

1. {x}^{2n+2}{y}^{4}-\frac{1}{3}{x}^{2n+3}{y}^{2n-3}+\frac{1}{9}{x}^{4}{y}^{2n-2}
2. {x}^{4n+2}{y}^{4}-\frac{2}{3}{x}^{2n+3}{y}^{2n-3}+\frac{1}{9}{x}^{4}{y}^{4n-2}
3. {x}^{4n+2}{y}^{4}-\frac{2}{3}{x}^{2n+3}{y}^{2n+1}+\frac{1}{9}{x}^{4}{y}^{4n-2}
4. {x}^{2n+2}{y}^{4}-\frac{2}{3}{x}^{2n+3}{y}^{2n-3}+\frac{1}{9}{x}^{4}{y}^{2n-2}

Solución:

Para resolver este problema sin recurrir a un desarrollo demasiado extenuante, vamos a aplicar el siguiente truco: llamaremos a {x}^{2n+1}{y}^{2}=a y al segundo término \frac{1}{3}{x}^{2}{y}^{2n-1}=b , de esta forma:

{\left({x}^{2n+1}{y}^{2}-\frac{1}{3}{x}^{2}{y}^{2n-1}\right)}^{2}\to {\left(a-b\right)}^{2}

Este producto notable es más sencillo de desarrollar.

{\left(a-b\right)}^{2}={a}^{2}-2ab+{b}^{2}

Ahora, vamos a calcular por separado cada uno de los términos.

{a}^{2}={\left({x}^{2n+1}{y}^{2}\right)}^{2}={\left({x}^{2n+1}\right)}^{2}{\left({y}^{2}\right)}^{2}={x}^{2\left(2n+1\right)}{y}^{4}={x}^{4n+2}{y}^{4}

Con este valor de {a}^{2} , descartamos a los incisos a y d. Vamos a calcular el siguiente término.

2ab=2\left({x}^{2n+1}{y}^{2}\right)\left(\frac{1}{3}{x}^{2}{y}^{2n-1}\right)=\frac{2}{3}{x}^{2n+1+2}{y}^{2+2n-1}=\frac{2}{3}{x}^{2n+3}{y}^{2n+1}

Entre el inciso b y c, el único cuyo segundo término corresponde con \frac{2}{3}{x}^{2n+3}{y}^{2n+1} es el c). Concluimos que la respuesta correcta es el inciso c).

Reactivo 26

¿Cuál es la expresión equivalente del siguiente producto?

(x-4)\left({x}^{2}+4x+16\right)

1. {x}^{3}-{x}^{2}+16
2. {x}^{3}+{x}^{2}+16
3. {x}^{3}+64
4. {x}^{3}-64

Solución:

En este caso podríamos desarrollar el producto entre el binomio y el trinomio, pero si analizamos bien las expresiones, vemos que {x}^{2} se obtiene al elevar a x al cuadrado, que 16 al elevar al 4 al cuadrado y que 4x se obtiene al multiplicar los términos del binomio.

Lo anterior indica que podemos utilizar la factorización para una diferencia de cubos:

{a}^{3}-{b}^{3}=\left(a-b\right)\left({a}^{2}+ab+{b}^{2}\right)

Apoyados en los anterior:

\left(x-4\right)\left({x}^{2}+4x+16\right)={x}^{3}-64

Examinando las opciones, concluimos que la respuesta correcta es la d).

Reactivo 27

¿Qué factorización corresponde al siguiente polinomio?

6{m}^{2}{n}^{2}-3{m}^{2}ns+2{m}^{2}{s}^{2}-4{m}^{2}ns

1. {m}^{2}(s-3n)(s-2n)
2. {m}^{2}(2n-3s)(n-2s)
3. {m}^{2}(2s-3n)(s-2n)
4. {m}^{2}(n-3s)(n-2s)

Solución:

Iniciamos extrayendo factor común a {m}^{2} .

6{m}^{2}{n}^{2}-3{m}^{2}ns+2{m}^{2}{s}^{2}-4{m}^{2}ns={m}^{2}\left(6{n}^{2}-3ns+2{s}^{2}-4ns\right)

Ahora, extraemos factor común 2n de 6{n}^{2}-3ns y 2s de 2{s}^{2}-4ns .

{m}^{2}\left(6{n}^{2}-3ns+2{s}^{2}-4ns\right)={m}^{2}\left[3n\left(2n-s\right)+2s\left(s-2n\right)\right]

Extraemos factor común el menos de s-2n .

{m}^{2}\left[3n\left(2n-s\right)+2s\left(s-2n\right)\right]={m}^{2}\left[3n\left(2n-s\right)-2s\left(2n-s\right)\right]

Finalmente, extraemos factor común 2n-s de ambos términos.

{m}^{2}\left[3n\left(2n-s\right)-2s\left(2n-s\right)\right]={m}^{2}\left(3n-2s\right)\left(2n-s\right)

Extraemos factor común de uno de los binomios y lo multiplicamos con el otro.

{m}^{2}\left(3n-2s\right)\left(-1\right)\left(s-2n\right)={m}^{2}\left(2s-3n\right)\left(s-2n\right)

Finalmente:

6{m}^{2}{n}^{2}-3{m}^{2}ns+2{m}^{2}{s}^{2}-4{m}^{2}ns={m}^{2}\left(2s-3n\right)\left(s-2n\right)

Comparando con las opciones del problema, concluimos que la correcta está en c).

Reactivo 28

Simplificar el siguiente producto:

\frac{2x-2}{{x}^{2}-9}\cdot \frac{5{x}^{2}+16x+3}{{x}^{2}-2x+1}\cdot \frac{{x}^{2}+5x-24}{5{x}^{2}+41x+8}

1. \frac{1}{x-1}
2. \frac{2}{x-1}
3. \frac{x}{x-1}
4. \frac{-2}{x-1}

Solución:

En este caso no se visualiza la posibilidad de aplicar la factorización para la diferencia de cubos. Solo nos queda factorizar a los polinomios tanto del numerador como del denominador. A {x}^{2}-9 le aplicamos diferencia de cuadrados.

Por otra parte, a {x}^{2}-2x+1 le buscamos dos números que sumados sean -2 y que multiplicados +1; estos son: -1 y -1.

\frac{2x-2}{{x}^{2}-9}\cdot \frac{5{x}^{2}+16x+3}{{x}^{2}-2x+1}\cdot \frac{{x}^{2}+5x-24}{5{x}^{2}+41x+8}=\frac{2\left(x-1\right)}{\left(x+3\right)\left(x-3\right)}\cdot \frac{5{x}^{2}+16x+3}{{\left(x-1\right)}^{2}}\cdot \frac{{x}^{2}+5x-24}{5{x}^{2}+41x+8}

Buscamos dos números que sumados den +5 y multiplicados -24 para el trinomio {x}^{2}+5x-24 . Estas cantidades son: -3 y +8.

=\frac{2\left(x-1\right)}{\left(x+3\right)\left(x-3\right)}\cdot \frac{5{x}^{2}+16x+3}{{\left(x-1\right)}^{2}}\cdot \frac{\left(x-3\right)\left(x+8\right)}{5{x}^{2}+41x+8}

En este punto podemos simplificar varios factores.

\frac{2\left(x-1\right)}{\left(x+3\right)\left(x-3\right)}\cdot \frac{5{x}^{2}+16x+3}{{\left(x-1\right)}^{2}}\cdot \frac{\left(x-3\right)\left(x+8\right)}{5{x}^{2}+41x+8}=\frac{2\left(x+8\right)}{\left(x+3\right)\left(x-1\right)}\cdot \frac{5{x}^{2}+16x+3}{5{x}^{2}+41x+8}

Para los otros dos trinomios es necesario aplicar la fórmula de segundo grado.

x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}

Para el trinomio 5{x}^{2}+16x+3 aplicando la fórmula obtenemos:

5{x}^{2}+16x+3=\left(x+\frac{1}{5}\right)\left(x+3\right)

Para el trinomio 5{x}^{2}+41x+8 aplicando la fórmula obtenemos:

5{x}^{2}+41x+8=\left(x+\frac{1}{5}\right)\left(x+8\right)

Sustituimos:

\frac{2\left(x+8\right)}{\left(x+3\right)\left(x-1\right)}\cdot \frac{5{x}^{2}+16x+3}{5{x}^{2}+41x+8}=\frac{2\left(x+8\right)}{\left(x+3\right)\left(x-1\right)}\cdot \frac{\left(x+\frac{1}{5}\right)\left(x+3\right)}{\left(x+\frac{1}{5}\right)\left(x+8\right)}

Simplificamos factores.

\frac{2\left(x+8\right)}{\left(x+3\right)\left(x-1\right)}\cdot \frac{\left(x+\frac{1}{5}\right)\left(x+3\right)}{\left(x+\frac{1}{5}\right)\left(x+8\right)}=\frac{2}{x-1}

Finalmente:

\frac{2x-2}{{x}^{2}-9}\cdot \frac{5{x}^{2}+16x+3}{{x}^{2}-2x+1}\cdot \frac{{x}^{2}+5x-24}{5{x}^{2}+41x+8}=\frac{2}{x-1}

Concluimos el problema seleccionando como respuesta correcta al inciso b).

Reactivo 29

Expresar el polinomio 16{x}^{4}-81{y}^{4} como el producto de polinomios.

1. \left(4{x}^{2}+9{y}^{2}\right)\left(2x+3y\right)\left(2x-3y\right)
2. \left(4{x}^{2}+9{y}^{2}\right)\left(x+y\right)\left(2x-3y\right)
3. \left(4{x}^{2}+9{y}^{2}\right)\left(2x-3y\right)\left(2x-3y\right)
4. \left(4{x}^{2}-9{y}^{2}\right)\left(2x+3y\right)\left(2x-3y\right)

Solución:

Iniciamos expresando a los coeficientes de x y y como potencias de exponente cuarto.

16{x}^{4}-81{y}^{4}={2}^{4}{x}^{4}-{3}^{4}{y}^{4}

Ahora expresamos todo como una potencia al cuadrado. Empleamos la propiedad de potencia de una potencia.

{2}^{4}{x}^{4}-{3}^{4}{y}^{4}={\left({2}^{2}{x}^{2}\right)}^{2}-{\left({3}^{2}{y}^{2}\right)}^{2}

Esto con la finalidad de aplicar diferencia de cuadrados.

{\left({2}^{2}{x}^{2}\right)}^{2}-{\left({3}^{2}{y}^{2}\right)}^{2}=\left(4{x}^{2}-9{y}^{2}\right)\left(4{x}^{2}+9{y}^{2}\right)

Aplicamos el mismo razonamiento para el binomio con signo negativo.

\left(4{x}^{2}-9{y}^{2}\right)\left(4{x}^{2}+9{y}^{2}\right)=\left({\left(2x\right)}^{2}-{\left(3y\right)}^{2}\right)\left(4{x}^{2}+9{y}^{2}\right)=\left(2x-3y\right)\left(2x+3y\right)\left(4{x}^{2}+9{y}^{2}\right)

Finalmente:

16{x}^{4}-81{y}^{4}=\left(2x-3y\right)\left(2x+3y\right)\left(4{x}^{2}+9{y}^{2}\right)

Comparando con los incisos, concluimos que la respuesta correcta es el inciso a).

Reactivo 30

Asociar el tipo de función con su ejemplo.

1. 1B, 2D, 3C, 4A, 5E
2. 1B, 2E, 3A, 4C, 5D
3. 1E, 2C, 3A, 4D, 5B
4. 1E, 2B, 3A, 4D, 5C

Solución:

El primer tipo de función indicado en la columna de la izquierda es: sinusoidal. Examinando la columna derecha, identificamos que la función sinusoidal está en el inciso B, por lo tanto: 1B. Con esta información descartamos a c) y d).

Una función racional es aquella fracción con polinomio en el numerador y denominador. De entre las 4 opciones restantes, la única que luego de una simplificación queda como una función racional es la E.

x-\left(\frac{1}{x}-2\right)=x-\frac{1-2x}{x}=\frac{{x}^{2}+2x-1}{x}

Con estas dos respuestas parciales: 1B, 2E, … tenemos información suficiente para concluir que la respuesta correcta es el inciso b).