Continuamos con la cuarta parte del simulador de Geometría y trigonometría para el examen del IPN, ahora vamos a resolver los ejercicios del 31 al 40.

Reactivo 31
Determinar la amplitud del ángulo central \alpha que se muestra en la siguiente configuración:

- 170°
- 160°
- 150°
- 140°
Solución:
Para llegar a la solución del problema, podemos aplicar la ecuación para el ángulo exterior de una circunferencia. Su definición dice que:
El ángulo exterior formado entre dos rectas que cortan cada una en dos puntos a una circunferencia, es igual a la semiresta del arco mayor con el arco menor.
\beta_{e x t}=\frac{\alpha-\gamma}{2}
La situación que se presenta en la figura es exactamente esa. Alfa corresponde al arco de mayor amplitud, mientras que \widehat{A B} es el de amplitud más pequeña y vale 100°. Por otro lado, el ángulo exterior \beta_{\text {ext }} es 30° como se indica en la ilustración.
Sustituyendo estos valores en la ecuación, podremos finalmente calcular el valor de alfa.
30^{\circ}=\frac{\alpha-100^{\circ}}{2}
\alpha=60^{\circ}+100^{\circ}
\alpha=160^{\circ}
Comparando con las opciones que ofrece el problema, la correcta es la b).
Reactivo 32
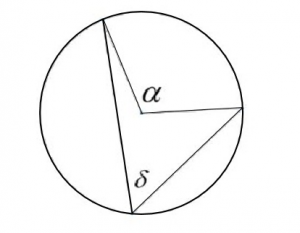
Determinar la amplitud del ángulo \delta si se sabe que la amplitud del ángulo central \alpha que subtiene es de 110° como se indica en la siguiente figura:
- 57°
- 55°
- 53°
- 51°
Solución:
Para resolver este primer problema, recurriremos a la relación entre el ángulo central y el ángulo inscrito de una circunferencia. Se sabe que:
\beta_{i}=\frac{\beta_{c}}{2}
El ejercicio ofrece como dato al ángulo central \beta_{c}=110^{\circ} , solo es necesario sustituir.
\beta_{i}=\frac{110^{\circ}}{2}=55^{\circ}
Concluimos entonces que la respuesta correcta es la b).
Reactivo 33
Calcular el área sombreada de la siguiente figura, sí \overline{A B}=10 \mathrm{~cm} ; \overline{B C}=15 \mathrm{~cm} \text{ y } \overline{C D}=5 \mathrm{~cm} y estos segmentos son diámetros de las circunferencias inscritas en la circunferencia de diámetro \overline{A D} .

- 125 \pi
- 5 \pi
- 75 \pi
- 25 \pi
Solución:
Para calcular el área solicitada, hay que darnos cuenta de que sin el resto de círculos inscritos, el área sería la mitad del que tiene como diámetro el segmento \overline{A D} . A esta se le resta la mitad del área del círculo \overline{A B} , la del círculo \overline{C D} y se le suma la mitad del círculo \overline{B C} .
Expresado en forma de ecuación, el área sombreada en azul sería:
A_{s}=\frac{A_{\overline{A D}}}{2}+\frac{A_{\overline{B C}}}{2}-\frac{A_{\overline{A B}}}{2}-\frac{A_{\overline{C D}}}{2}
Como recordatorio, la fórmula para calcular el área de un círculo es:
A_{s}=\pi r^{2}=\pi \frac{D^{2}}{4}
Sustituyendo nos queda:
A_{s}=\pi \frac{\overline{A D}^{2}}{4}+\pi \frac{\overline{B C}^{2}}{4}-\pi \frac{\overline{A B}^{2}}{4}-\pi \frac{\overline{C D}^{2}}{4}
Del enunciado sabemos que:
\overline{A B}=10 \mathrm{~cm}
\overline{B C}=15 \mathrm{~cm}
\overline{C D}=5 \mathrm{~cm}
\overline{A D}=\overline{A B}+\overline{B C}+\overline{C D}=30 \mathrm{~cm}
Sustituimos los valores respectivos y concluimos con la resolución del problema:
A_{s}=\pi \frac{30^{2}}{4}+\pi \frac{15^{2}}{4}-\pi \frac{10^{2}}{4}-\pi \frac{5^{2}}{4}=125 \pi
De las opciones que da el problema, la correcta es la a).
Reactivo 34
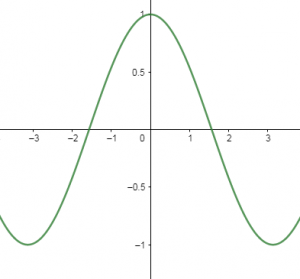
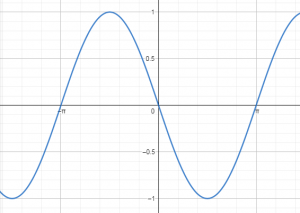
¿Cuál es la representación gráfica de \frac{1}{\cos \theta} ?
Solución:
Según las identidades trigonométricas básicas, el opuesto multiplicativo del coseno es la secante, por tanto:
\frac{1}{\cos \theta}=\sec \theta
Se podría determinar la respuesta correcta al investigar cuál es la gráfica de la secante, pero es más interesante analizar su comportamiento para determinados valores y llegar así a la respuesta correcta.
Los signos para el coseno según el cuadrante son:
- Primer y cuarto cuadrantes positivos
- Segundo y tercer cuadrante negativo
Por simple aritmética, el opuesto multiplicativo del coseno \frac{1}{\cos \theta} cumplirá con la misma característica de signos en esos cuadrantes.
El coseno y su opuesto \frac{1}{\cos \theta} para determinados ángulos notables:

Con el estudio anterior queda claro que las opciones a) y b) no pueden ser la respuesta. Ambas son continuas para todo R y \frac{1}{\cos \theta} presenta discontinuidades en múltiplos impares de \frac{\pi}{2} .
La opción c) tampoco corresponde, porque tiene una discontinuidad en cero y \frac{1}{\cos \theta} es continua en ese punto, vale exactamente 1.
La opción d) encaja a la perfección. Es acotada en 0, \pi y \pi (tal como se muestra en la imagen) y discontinua tanto en \frac{\pi}{2} como en - \frac{\pi}{2} con las respectivas tendencias a los laterales de dichos valores.
Conclusión: la respuesta correcta es la d).
Reactivo 35
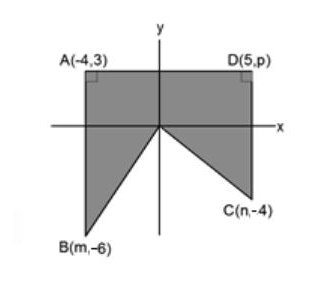
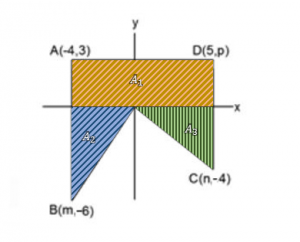
Determinar el valor del área en la siguiente figura:
- 51 u^{2}
- 47 u^{2}
- 49 u^{2}
- 59 u^{2}
Solución:
Comencemos por completar las coordenadas en los puntos de la imagen.
El punto B tiene como coordenadas m y -6, ya que A(-4,3) es paralelo respecto al eje x de B ambos tienen la misma coordenada en x. Por lo tanto B(-4,-6) .
El punto C tiene como coordenadas n y -4. D y C son también paralelos respecto al eje x, eso quiere decir que poseen la misma coordenada en x. Por lo tanto C(5,-4) .
El punto D tiene como coordenada faltante a p. Como es paralelo al punto A respecto al eje y, ambos poseen la misma coordenada en y. Por lo tanto D(5,3) .
Conocidos los puntos, nos queda solo dividir el dibujo en figuras simples como rectángulos y triángulos. En la parte superior podemos identificar un rectángulo y en la inferior 2 triángulos rectángulos. Las áreas quedarían divididas de la siguiente manera:
El área total de la figura sería:
A=A_{1}+A_{2}+A_{3}
El área 1 es un rectángulo de base 9cm (medida desde el punto A hasta el punto D) y altura de 3cm:
A_{1}=9 * 3=27 \mathrm{~cm}^{2}
El área 2 es un triángulo rectángulo de base 4cm y de altura 6cm:
A_{2}=\frac{4 * 6}{2}=12 \mathrm{~cm}^{2}
El área 3 es también un triángulo de base 5cm y de altura 4cm:
A_{3}=\frac{5 * 4}{2}=10 \mathrm{~cm}^{2}
Finalmente:
A=27 \mathrm{~cm}^{2}+12 \mathrm{~cm}^{2}+10 \mathrm{~cm}^{2}=49 \mathrm{~cm}^{2}
Comparando con las opciones del problema, la respuesta correcta sería la c).
Reactivo 36
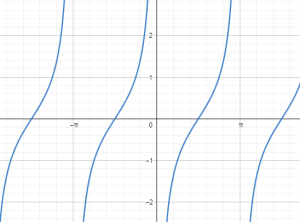
Identificar la gráfica de la función trigonométrica que cumpla las siguientes características:
- Sea una función impar
- Sea discontinua para los siguientes valores \left\{x \in R \mid x=\frac{\pi}{2}+k \pi, k \in Z\right\}
- No es acotada
- Siempre es creciente en intervalos
Solución:
Para resolver el problema, analizaremos cada una de las condiciones impuestas en el enunciado.
Sea función impar:
Una función se considera impar si f(-x)=-f(x) , es decir que si la gráfica se rota 180° respecto al origen se obtiene la misma representación. Otra forma de verlo, es identificando simetría en diagonal respecto al origen.
La opción a y b cumplen con tener simetría impar, por lo que descartamos de primera mano a c y d.
Sea discontinua para los valores \left\{x \in R \mid x=\frac{\pi}{2}+k \pi, k \in Z\right\} :
La opción b) precisamente es discontinua para x=\frac{\pi}{2}+k \pi , es decir, para múltiplos impares de \frac{\pi}{2} . Por su parte, la opción a) es continua para todo R , al no cumplir con la segunda condición solo queda la b).
No es acotada y Siempre es creciente en intervalos
La grafica del inciso b) no posee un rango acotado, por el contario el rango se extiende entre menos y más infinito. Además, siempre es creciente entre los intervalos \left(\frac{\pi}{2}+k \pi, \frac{\pi}{2}+(k+1) \pi\right) desde menos infinito hasta más infinito.
Sin más por analizar, la opción b) cumple todas las condiciones impuestas. Seleccionamos como respuesta correcta a b). La gráfica corresponde a la función \tan (x) .
Reactivo 37
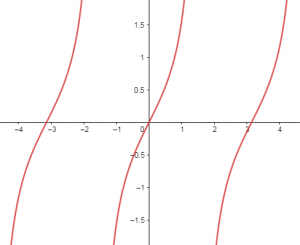
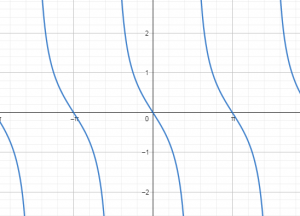
Identificar la gráfica de la función f(\varphi)=-\tan (\varphi) .
Solución:
Para resolver el problema, nos valdremos de analizar la gráfica que debería tener pos si sola la tangente, multiplicando luego los valores obtenidos por -1 tendríamos entonces el comportamiento de -\tan (\varphi) .
La tangente posee la siguiente relación de signos por cuadrante:
- Primer y tercer cuadrante positivo
- Segundo y cuarto cuadrante negativo
Es decir que -\tan (\varphi) debe ser:
- Primer y cuarto cuadrante negativo
- Segundo y tercer cuadrante positivo
La tangente al igual que -\tan (\varphi) son discontinuas para \varphi=\frac{\pi}{2}+k \pi , ambas pasan por cero. Esto reduce las opciones entre a) y b).
Además, la tangente tiende a +\infty en \frac{\pi}{2} por la izquierda y a -\infty por la derecha. Eso quiere decir que -\tan (\varphi) tiende a -\infty en \frac{\pi}{2} por la izquierda y a +\infty por la derecha. Con todo este análisis, queda claro que la respuesta correcta es la b).
Reactivo 38
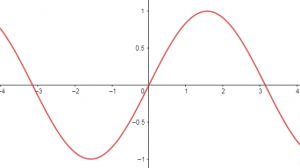
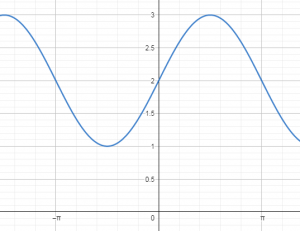
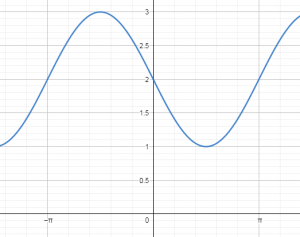
Identificar la gráfica que corresponde a la función: y=2-\sin (x) .
Solución:
La gráfica del seno por sí sola pasa por el origen, es máxima positiva en \frac{\pi}{2} y vuelve a cero en \pi , todo eso en el primer y segundo cuadrante.
La función solicitada tiene al menos seno con el eje de simetría desplazado a 2 en el eje de las y . Por tanto, al pasar por cero el resultado será 2, en \frac{\pi}{2} será máxima negativa dando como resultado 1 y en \pi valdrá de nuevo 2.
y=2-\sin (0)=2
y=2-\sin \left(\frac{\pi}{2}\right)=2-1=1
y=2-\sin (\pi)=2-0=2
Comparando con las gráficas de los incisos, la opción correcta sería la a).
Reactivo 39
Identificar las cotas de la función: f(x)=\sin (x)
- \pi, 2 \pi
- 0,2 \pi
- 0, 1
- 1, -1
Solución:
La función seno posee como valor máximo 1 y como valor mínimo -1. Es decir, su rango está acotado en el intervalo [-1,1] . Fácilmente, podemos concluir que las cotas de f(x)=\sin (x) son 1 y -1.
La respuesta correcta es la d).
Reactivo 40
Determinar la igualdad de la expresión: \operatorname{sen}^{2} 2 x\left(\csc ^{2} 2 x-1\right)
- \cos ^{2} 2 x
- \operatorname{sen}^{2} 2 x
- \cot ^{2} 2 x
- \operatorname{tg}^{2} 2 x
Solución:
De la identidad pitagórica escrita en términos de cotangente y cosecante sabemos que:
\cot ^{2} x+1=\csc ^{2} x
Despejando queda:
\cot ^{2} x=\csc ^{2} x-1
Sustituimos en la expresión que estamos simplificando:
\operatorname{sen}^{2} 2 x\left(\csc ^{2} 2 x-1\right)=\operatorname{sen}^{2} 2 x \cot ^{2} 2 x
Escribimos a cotangente en términos de seno y coseno, siguiendo con la recomendación general de trabajar el seno con coseno:
\operatorname{sen}^{2} 2 x \cot ^{2} x 2=\operatorname{sen}^{2} 2 x \frac{\cos ^{2} 2 x}{\operatorname{sen}^{2} 2 x}
Simplificamos y nos queda finalmente que:
\operatorname{sen}^{2} 2 x \frac{\cos ^{2} 2 x}{\operatorname{sen}^{2} 2 x}=\cos ^{2} 2 x
\operatorname{sen}^{2} 2 x\left(\csc ^{2} 2 x-1\right)=\cos ^{2} 2 x
Comparando con las opciones que ofrece el problema, la correcta sería a).