Hola aspirante, ¿Vas a presentar el Exani II de Ceneval? En este simulador de examen vamos a resolver 50 reactivos correspondientes al área de pensamiento matemático, recuerda que en tu examen de admisión vendrán 30 reactivos correspondientes a esta área.

Diseñamos este examen simulador de pensamiento matemático para que refuerces, repases y practiques todos los temas de matemáticas que vendrán en tu examen de admisión, por lo que es muy importante que antes de consultar las respuestas, intentes resolverlo por tu propia cuenta.
Toma en cuenta lo siguiente:
- Además de explicar la solución en este tutorial, vamos a resolver los ejercicios del simulador en clases en vivo, la recomendación es exactamente la misma, primero intenta resolverlos en tu cuaderno.
- Dividimos el simulador en 5 partes, en la primera parte vamos a resolver los reactivos del 1 al 10.
- En cada reactivo encontrarás el problema junto con la explicación de la respuesta correcta.
Antes de comenzar te voy a dar una breve introducción a lo que es el Exani II de Ceneval, además de mostrarte el temario de pensamiento matemático, si ya conoces esta información simplemente deslízate hacia abajo y comienza con el examen.
¿Cómo es el Exani II?
El nuevo Exani II de Ceneval es un examen de admisión que se caracteriza por evaluar conocimientos generales, y específicos relacionados con el área de estudio de tu carrera.
Es decir, que cada carrera tiene su propia estructura de examen, que a grandes rasgos es:
- Pensamiento matemático
- Comprensión lectora
- Redacción indirecta
- Módulo 1 + Módulo 2
No importante la carrera a la que apliques las primeras 3 materias vienen en todas las versiones del examen.
¿Es la primera vez que vas a presentar el examen? Es importante que conozcas tanto la estructura como el temario completo de la guía Exani II.
Por lo que te recomiendo que además de practicar con este examen simulacro, te informes sobre la estructura y las partes del examen.
Estructura del examen
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
El examen diagnóstico de inglés no cuenta para tu resultado final, incluso es probable que tu universidad no lo aplique.
Temario de Pensamiento matemático
Si ya descargaste la guía, quizás ya te diste cuenta de que el temario es un bastante extenso, ya que prácticamente se incluyen todos los temas de las materias de matemáticas, a excepción de cálculo que se incluye en uno de los módulos específicos.
Pensamiento matemático se divide en dos grandes subáreas que abarcan el temario completo:
Subárea: Comprensión de lo matemático
- Sentido numérico
- Inecuaciones lineales
- Simplificación de expresiones algebraicas
- Razones trigonométricas
- Área
- Desviación estándar
- Media aritmética
- Conexiones
- Razones y proporciones
- Interpretación gráfica de ecuaciones lineales
- Ejes de simetría
- Estimación de trayectorias
- Frecuencias
- Probabilidad clásica de eventos simples
- Estimaciones
- Leyes de los exponentes
- Porcentaje
- Unidades de medida como patrón de comparación
- Espacio muestral
Subárea: Matematización
- Desarrollo de usos
- Representación gráfica de ecuaciones de segundo grado
- Comportamiento gráfico de funciones cuadráticas
- Relaciones trigonométricas
- Representación gráfica de información
- Medidas de tendencia central y de dispersión
- Lenguaje matemático
- Polinomios
- Sistemas de ecuaciones lineales con dos y tres incógnitas
- Resignificaciones
- Variación lineal tabular
- Medidas de posición (deciles, cuartiles y percentiles)
Si bien matemáticas suele ser la materia que se considera más difícil, toma en cuenta que en tu examen vendrán 30 reactivos de los 138, por lo que es igual de importante estudiar español, así como los módulos específicos.
Simulacro pensamiento matemático
Antes de comenzar a resolver el simulacro es importante que sigas las siguientes recomendaciones, esto para aprovechar al máximo la experiencia de realizar un examen de prueba, previo al examen real Exani II.
Recomendaciones:
- Mide tus tiempos: Usa la app de tu celular para medir cuanto tiempo tardas en responder estos primeros 10 reactivos.
- Usa una calculadora sencilla: Ceneval te permite el uso de una calculadora sencilla, por lo que si vas a usar una, asegúrate de que no sea científica para que no te acostumbres, aunque lo mejor es intentar hacer las operaciones a mano para subir la dificultad.
- Identifica los reactivos más difíciles: Toma notas de los reactivos que se te hagan más complicados e identifica el tema para después estudiarlo en profundidad.
- Revisa las respuestas hasta el final: Compara tus respuestas con las del simulacro y asígnate una calificación.
- Evita distracciones: No pares hasta terminarlo, y asegúrate de hacerlo en un ambiente tranquilo.
El principal objetivo de este examen simulacro de pensamiento matemático es que identifiques los temas que más se te compliquen, sin más que decir comenzamos.
Reactivo 1
Un estudiante se encuentra a 20 m de una estructura para la que debe hacer un modelo a escala. El estudiante observa la parte alta de este y se da cuenta de que forma un ángulo de depresión de 45° paralelo a su línea de visión (línea punteada).
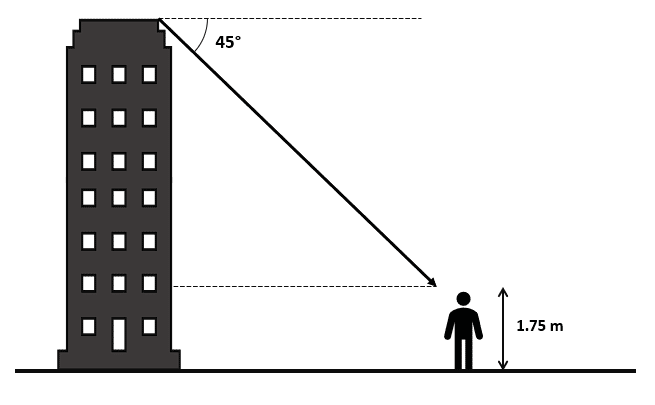
Considere que:
\begin{array}{c}\mathrm{sin}45°=0.707\\ \mathrm{cos}45°=0.707\\ \mathrm{tan}45°=1\end{array}¿Cuál debe ser la altura del edificio a escala, si el mismo debe ser 26 veces más pequeño que el original?
- 42 m
- 84 m
- 84 m
Solución:
Para resolver el problema, debemos identificar el triángulo que se forma entre el ángulo de depresión, la distancia entre el edificio y el estudiante, y la diagonal desde la punta hasta su línea de visión.
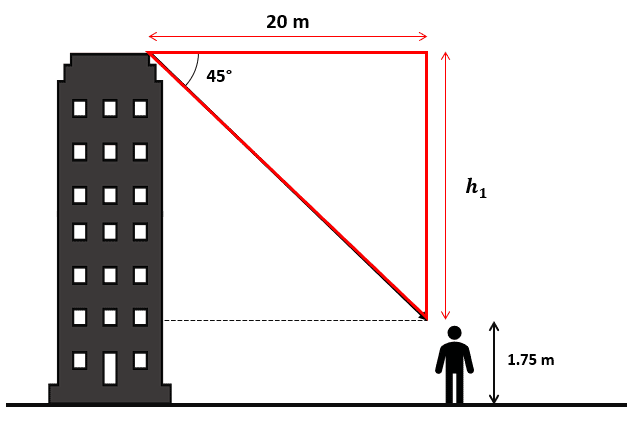
De la imagen podemos identificar dos cosas: que a partir del triángulo se obtiene a la altura {h}_{1} y que la altura total del edificio se obtiene sumándole a {h}_{1} los 1.75 metros de altura del estudiante.
Aplicando la tangente al ángulo de depresión, obtenemos:
\mathrm{tan}45°=\frac{{h}_{1}}{20}\to {h}_{1}=20\mathrm{tan}45°
Sustituimos el valor numérico de la tangente de 45°.
{h}_{1}=20 \mathrm{m}
De esta manera, la altura total del edificio se obtiene como:
h=20+1.75=21.75 \mathrm{m}
Como último paso, nos queda dividir la altura por el factor de escala para la maqueta.
{h}_{m}=\frac{h}{26}=\frac{21.75}{26}=0.837 \mathrm{m}\approx 0.84 \mathrm{m}
La maqueta del edificio debe tener una altura de 0.84 metros.
Concluimos indicando como respuesta correcta al inciso c).
Reactivo 2
En base a la imagen que se muestra a continuación, indique cuál de las opciones representa el valor de su área sombreada.
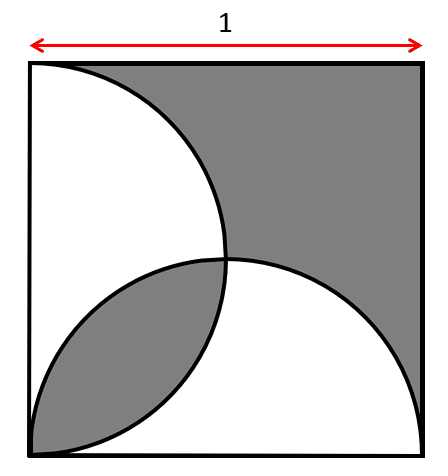
- 2-\frac{3}{8}\pi
- \frac{1}{2}
- \frac{3}{2}-\frac{\pi }{8}
Solución:
En este caso, la disposición de las figuras dentro del cuadrado dificulta encontrar un mecanismo rápido para calcular el área sombreada.
Vamos a dividir a la figura en 4 partes iguales para simplificar la solución, de tal forma que: el área sombreada total será igual a la fracción sombreada en cada parte.
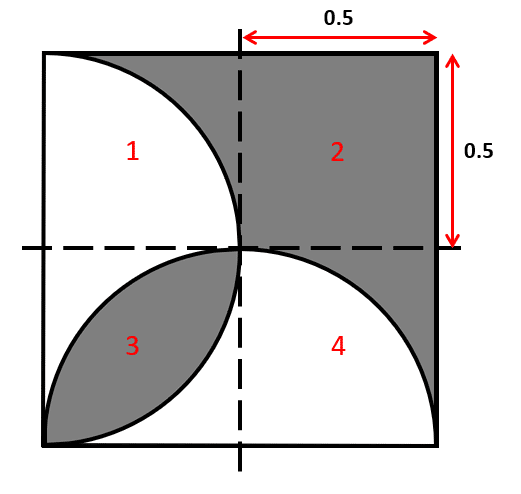
De esta forma:
{A}_{s}={A}_{s1}+{A}_{s2}+{A}_{s3}+{A}_{s4}
Vamos con la solución de la fracción número 3, ya que es la más complicada. Examinando a la fracción, vemos que podemos descomponerla de la siguiente forma:
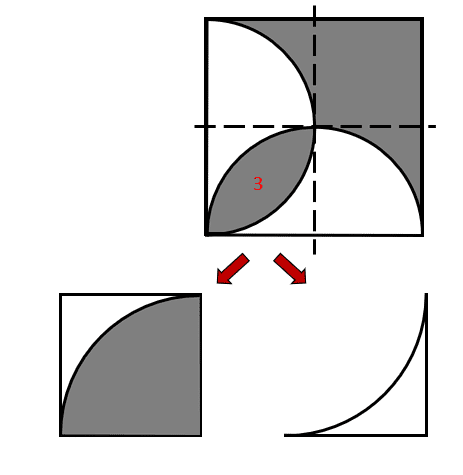
A su vez, cada una de las áreas puede obtenerse como:
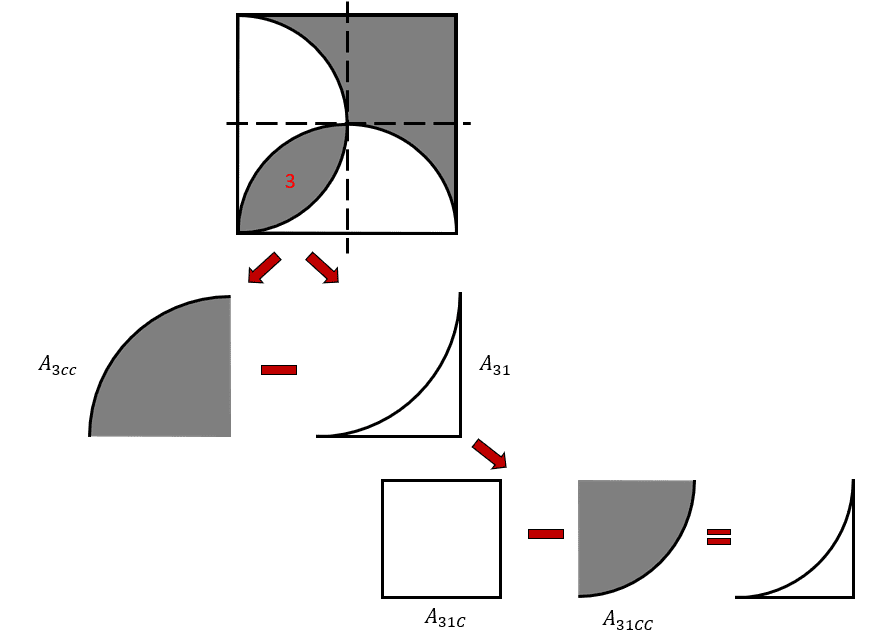
A partir de la imagen anterior, podemos trabajar las áreas de una forma algebraica.
{A}_{3}={A}_{3CC}-{A}_{31}
{A}_{31}={A}_{31C}-{A}_{31CC}
Sustituyendo la segunda ecuación en {A}_{3} :
{A}_{3}={A}_{3CC}-{A}_{31C}+{A}_{31CC}
Ahora cada una de las áreas corresponde a:
- {A}_{3CC} y {A}_{31CC} son el área de un cuarto de circunferencia de radio igual a 0.5 .
- {A}_{31C} es el área de un cuadrado de lado igual a 0.5 .
{A}_{3CC}={A}_{31CC}=\frac{\pi {r}^{2}}{4}
{A}_{31C}={a}^{2}
Sustituimos en la ecuación de {A}_{3} :
{A}_{3}=\frac{\pi {r}^{2}}{4}-{a}^{2}+\frac{\pi {r}^{2}}{4}=\frac{\pi {r}^{2}}{2}-{a}^{2}
Sustituimos los valores para a y r .
{A}_{3}=\frac{\pi }{8}-\frac{1}{4}
Una vez calculada el área más compleja, vamos con el resto.
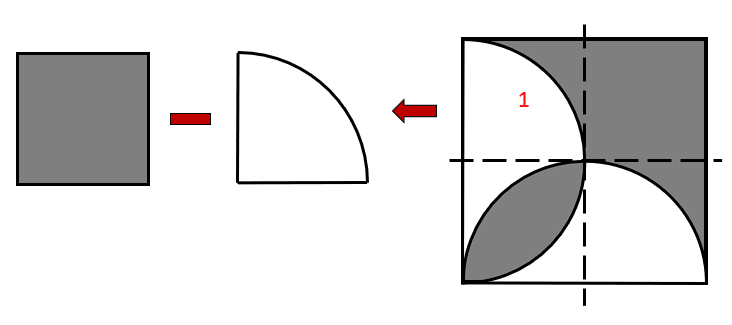
El área 1 es igual al área de un rectángulo de lado 0.5 menos un cuarto de circunferencia de radio 0.5 .
{A}_{1}={a}^{2}-\frac{\pi {r}^{2}}{4}=\frac{1}{4}-\frac{\pi }{16}
El área 2 es igual a un cuadrado de lado 0.5 mientras que el área 4 es igual al área 1.
{A}_{2}=\frac{1}{4}, {A}_{4}=\frac{1}{4}-\frac{\pi }{16}
Finalmente, el área sombreada de toda la figura es:
{A}_{s}={A}_{1}+{A}_{2}+{A}_{3}+{A}_{4}=\left(\frac{1}{4}-\frac{\pi }{16}\right)+\frac{1}{4}+\left(\frac{\pi }{8}-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{\pi }{16}\right)=\frac{1}{2}
Analizando el resultado, vemos que es equivalente a medio cuadrado de lado 1. Esto es porque las zonas grises de las partes 1 y 4, rellenan los espacios en blanco de la figura 3, formando así otro cuadrado de lado 0.5 .
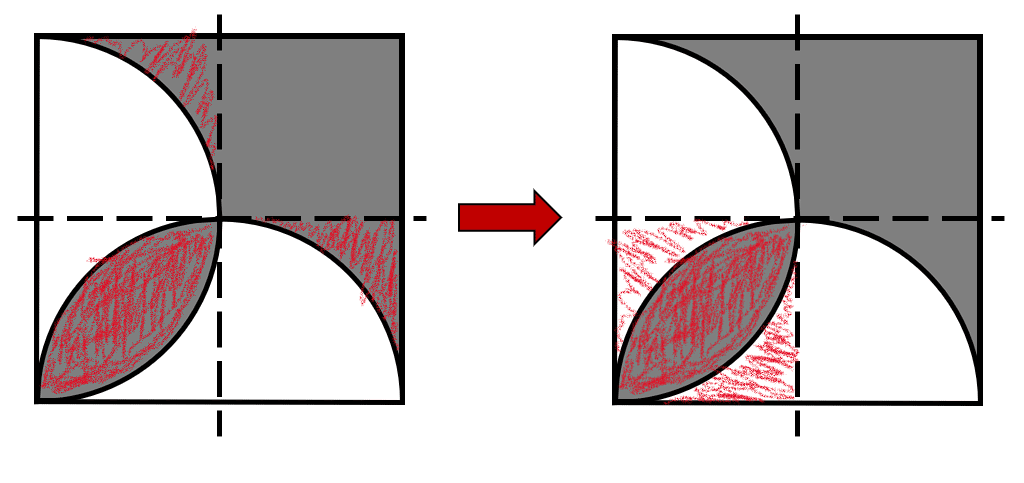
La respuesta correcta al ejercicio es el inciso b).
Reactivo 3
¿Qué opción es equivalente a la expresión \frac{\left({x}^{2}+x-2\right)\left(x+3\right)}{{x}^{2}+5x+6} ?
- \frac{1}{x-1}
- \left(x-1\right)
- \left(x+1\right)
Solución:
A simple vista, no hay simplificaciones entre los polinomios del numerador y el denominador. Por esta razón, debemos factorizar a los trinomios del numerador y el denominador.
Trinomio del numerador.
{x}^{2}+x-2
Buscamos a dos números que sumados sean +1 y que multiplicados -2.
{x}^{2}+x-2=\left(x+2\right)\left(x-1\right)
Trinomio del denominador.
{x}^{2}+5x+6
Ahora, toca buscar a dos números que sumen +5 y cuyo producto sea +6.
{x}^{2}+5x+6=\left(x+2\right)\left(x+3\right)
Sustituimos en la fracción.
\frac{\left({x}^{2}+x-2\right)\left(x+3\right)}{{x}^{2}+5x+6}=\frac{\left(x+2\right)\left(x-1\right)\left(x+3\right)}{\left(x+2\right)\left(x+3\right)}
Simplificamos:
\frac{\left(x+2\right)\left(x-1\right)\left(x+3\right)}{\left(x+2\right)\left(x+3\right)}=x-1
La respuesta correcta es el inciso b).
Reactivo 4
Un grupo de 7 amigos van a cenar a un restaurante y dos de ellos quieren sentarse juntos en la mesa con forma redonda. ¿De cuántas maneras se pueden sentar el resto de amigos alrededor de la pareja?
- 60
- 140
- 120
Solución:
Para resolver cualquier problema de conteo, debemos darnos cuenta que se trata de una permutación circular. La ecuación para calcular permutaciones circulares es:
P{C}_{n}^{m}=\left(m-n\right)!
En este caso, m es el total de elementos y n son los elementos que se mantienen fijos.
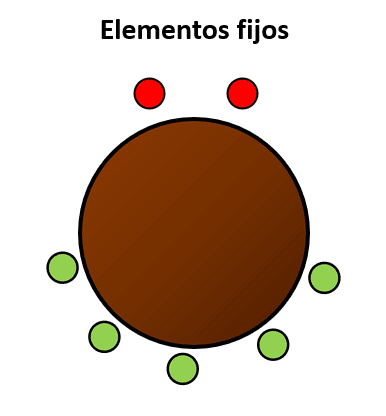
Sustituimos en la ecuación:
P{C}_{2}^{7}=\left(7-2\right)!=120
El resto de amigos pueden acomodarse de 120 formas distintas.
La respuesta correcta es el inciso c).
Reactivo 5
Un emprendedor tiene dos alternativas de negocio para implementar en su local. La primera, consiste en adquirir en mayoreo 1000 piezas de computadoras cada una por el precio de 10$, pero el máximo margen de ganancias a percibir es del 33%.
La segunda, consta en adquirir piezas en mercados nacionales con un costo de 18$ por unidad, con una ganancia máxima del 25%. ¿Cuántas piezas debe comprar el emprendedor en mercados nacionales para que sea mejor alternativa que la importación?
- x>733
- x<733
- x\ge 733
Solución:
Para responder a la pregunta del enunciado, debemos calcular la ganancia final en pesos para cada una de las alternativas. Luego, debemos calcular el volumen de compra para la segunda alternativa con base en la primera.
Recordemos que la ganancia de un producto se calcula como la resta entre su precio de venta y su precio de adquisición.
G=PV-PA
Primera alternativa.
El precio de adquisición en este caso es de 10$, mientras que el precio de venta se calcula como:
P{V}_{1}=P{A}_{1}\left(1+{\%}_{1}\right)=10\left(1+0.33\right)=13.3\$
Las ganancias netas son:
{G}_{1}=13.3-10=3.3\$
Segunda alternativa.
Aplicando el mismo razonamiento nos queda:
{G}_{2}=18\left(1+0.25\right)-18=4.5\$
Ahora, las ganancias por el cargamento entero de las piezas importadas son:
G{T}_{1}=1000\cdot 3.3\$=3300\$
Si el volumen de compra para la alternativa 2 es V{C}_{2} , podemos despejar su mínimo valor de la siguiente inecuación:
4.5V{C}_{2}>3300\$\to V{C}_{2}>733.33
El emprendedor debe comprar más de 733 unidades en mercados nacionales para que sea una mejor alternativa que la importación. La respuesta correcta es el inciso a).
Reactivo 6
María tiene una tienda de decoraciones y planea ofrecer una promoción a sus clientes. La oferta consiste en 1 arreglo de flores y 1 caja de bombones importados a 520$. Ella calcula que con su oferta aumentará en un 35% los pedidos de arreglos y cajas de bombones. Si el arreglo cuesta 330$ y los bombones rellenos 260$, ¿cuál es la diferencia en ganancias que obtiene María?
- 125 pesos por venta
- 80 pesos por venta
- 130 pesos por venta
Solución:
Debemos calcular por separado las ganancias con y sin la promoción. En el caso de la promoción, el flujo de ventas debe estimarse con el 35% de aumento en los pedidos y con un precio total de 520$.
Por otra parte, al no considerar la promoción se estima el flujo de ventas de siempre y los predios de cada producto son los indicados por el enunciado. Debido a que no conocemos el flujo de ventas, lo trataremos como un parámetro FV .
Ingresos brutos con la promoción.
I{B}_{cp}=520\cdot FV\cdot 1.35=720FV
Ingresos brutos sin la promoción.
I{B}_{sp}=\left(330+260\right)\cdot FV=590FV
La diferencia se obtiene como:
I{B}_{cp}-I{B}_{sp}=720FV-590FV=130FV
Estas ganancias están referidas al total del flujo de ventas base. Dividimos entre FV para encontrar la diferencia por venta:
\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{i}\mathrm{a}=\frac{130\mathrm{F}\mathrm{V}}{\mathrm{F}\mathrm{V}}=130 \$
María va a ganar 130$ extras al implementar su promoción.
Concluimos que la respuesta correcta es el inciso c).
Reactivo 7
¿Cuál de las siguientes expresiones permiten calcular el valor del dinero en el tiempo con interés compuesto?
- S=P\left(1+{i}^{n}\right)
- S=P{\left(1+i\right)}^{n}
- S=P\left(1+ni\right)
Solución:
En matemáticas financieras, el interés compuesto es aquel que se agrega al capital inicial teniendo en cuenta el resto de intereses. En este caso P es el capital inicial, S es el valor del dinero en el periodo actual, i es la tasa de interés y n es el período actual.
El interés compuesto en el periodo n se calcula a partir de la siguiente ecuación:
S=P{\left(1+i\right)}^{n}
Comparando con los incisos, concluimos que la respuesta correcta es el b).
Reactivo 8
¿Qué significa que la desviación estándar para un conjunto de datos sea grande?
- Que los resultados tienen poca relación unos entre otros
- Que la media es un valor muy grande
- Que los datos se encuentran dispersos unos de otros
Solución:
En estadística descriptiva, la desviación típica nos permite obtener una medida acerca de cuán alejados se encuentra un conjunto de datos respecto a su media aritmética.
\sigma =\sqrt{\frac{\sum {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{N}}
En consecuencia, una desviación típica alta implica que los datos se encuentran separados en mayor medida respecto a la media, es decir, una mayor diferencia {\left({x}_{i}-\stackrel{-}{x}\right)}^{2} . Concluimos entonces que la respuesta correcta es el inciso c).
Todas las partes del Simulacro:
Reactivo 9
En la línea de producción de una empresa, se fabrican 400 piezas al día con la ayuda de 4 máquinas especializadas. Cada una de ellas genera piezas defectuosas, tal como se muestra en la siguiente tabla.

Determine la media de piezas defectuosas que salen de la línea de producción por día.
- 8.75
- 10
- 5
Solución:
En este caso, debemos calcular la media de las piezas defectuosas de toda la línea de producción en un día. Los datos para realizar los cálculos se extraen de la tabla suministrada por el enunciado.
\stackrel{-}{pd}=\frac{{l}_{1}+{l}_{2}+{l}_{3}+{l}_{4}}{N}
Sustituimos N=4 y los respectivos valores para cada línea de producción.
\stackrel{-}{pd}=\frac{10+5+12+8}{4}=8.75
Las líneas de producción, en promedio, hacen 8.75 piezas defectuosas en un día laboral.
La respuesta correcta es el inciso a).
Reactivo 10
En la tabla se muestra la intensidad de corriente en vacío de los sensores que fabrica una empresa tecnológica, agrupada en conjuntos.
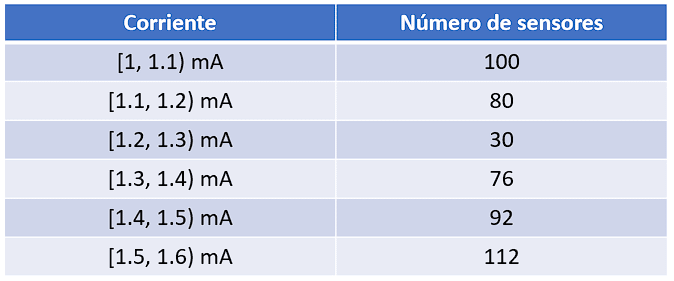
¿Cuál es la mediana del conjunto de datos agrupados?
- 1.346 \mathrm{m}\mathrm{A}
- 1.46 \mathrm{m}\mathrm{A}
- 1.3 \mathrm{m}\mathrm{A}
Solución:
De los temas referentes a la estadística descriptiva, sabemos que la mediana de un conjunto de datos es aquel valor que lo divide en dos partes iguales. En el caso de datos agrupados por intervalos, la mediana se calcula como:
{M}_{e}={L}_{i}+\frac{{P}_{i}-{F}_{i-1}}{{f}_{i}}\cdot {A}_{i}
Donde:
- {P}_{i} es la posición de la mediana. Se usa \frac{n}{2} cuando los datos son pares y \frac{n+1}{2} cuando son impares
- {L}_{i} es el límite inferior de la clase modal
- {f}_{i} es la frecuencia absoluta de la clase modal
- {F}_{i-1} es la frecuencia acumulada de la clase anterior
- {A}_{i} es la amplitud de la clase modal
Iniciamos por adicionar una columna a la tabla con la frecuencia absoluta acumulada.
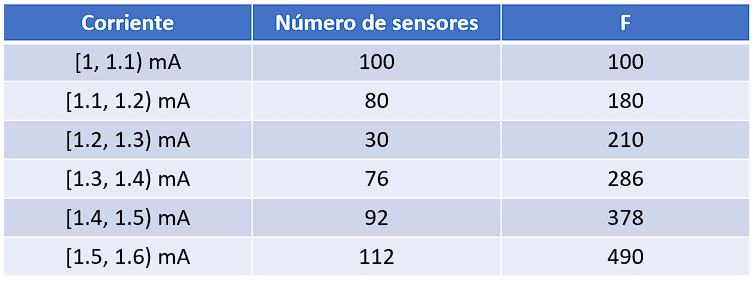
El total de datos es par: 490. Por esta razón, calculamos la posición como:
{P}_{i}=\frac{n}{2}=\frac{490}{2}=245
La clase modal será la primera en tener su frecuencia absoluta acumulada mayor o igual a 245. Examinando la tabla, sería la clase \left[1.3, 1.4\right) \mathrm{m}\mathrm{A} .
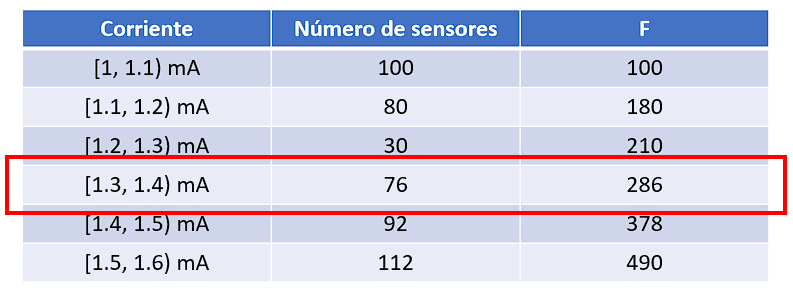
Extraemos el resto de datos a partir de la clase.
{L}_{i}=1.3, {f}_{i}=76, {F}_{i-1}=210, {A}_{i}=0.1
Sustituimos en la ecuación de la media:
{M}_{e}=1.3+\frac{245-210}{76}\cdot 0.1=1.346 \mathrm{m}\mathrm{A}
La mediana de las corrientes en vacío de los sensores es de 1.346 mA.
La respuesta correcta es el inciso a).


