Continuamos con la segunda parte el examen simulacro de pensamiento matemático para el examen de ingreso a la universidad Exani II de Ceneval, vamos a resolver los reactivos del 11 al 20.

Recuerda que además de matemáticas debes de estudiar los temas de comprensión lectora, redacción indirecta y los dos módulos específicos que le corresponden a tu carrera, si no los conoces ingresa a la guía exani II.
Estructura del Exani II
El Exani II de Ceneval tiene un total de 168 reactivos, dividiéndose en diferentes módulos, para que te familiarices con la estructura de la prueba, puedes ver la siguiente tabla:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Temario de Pensamiento matemático
Pensamiento Matemático es uno de los módulos generales del examen, por lo que es importante familiarizarte con esta parte de la prueba. Aquí puedes ver el temario completo.
Subárea: Comprensión de lo matemático
- Sentido numérico
- Inecuaciones lineales
- Simplificación de expresiones algebraicas
- Razones trigonométricas
- Área
- Desviación estándar
- Media aritmética
- Conexiones
- Razones y proporciones
- Interpretación gráfica de ecuaciones lineales
- Ejes de simetría
- Estimación de trayectorias
- Frecuencias
- Probabilidad clásica de eventos simples
- Estimaciones
- Leyes de los exponentes
- Porcentaje
- Unidades de medida como patrón de comparación
- Espacio muestral
Subárea: Matematización
- Desarrollo de usos
- Representación gráfica de ecuaciones de segundo grado
- Comportamiento gráfico de funciones cuadráticas
- Relaciones trigonométricas
- Representación gráfica de información
- Medidas de tendencia central y de dispersión
- Lenguaje matemático
- Polinomios
- Sistemas de ecuaciones lineales con dos y tres incógnitas
- Resignificaciones
- Variación lineal tabular
- Medidas de posición (deciles, cuartiles y percentiles)
Reactivo 11
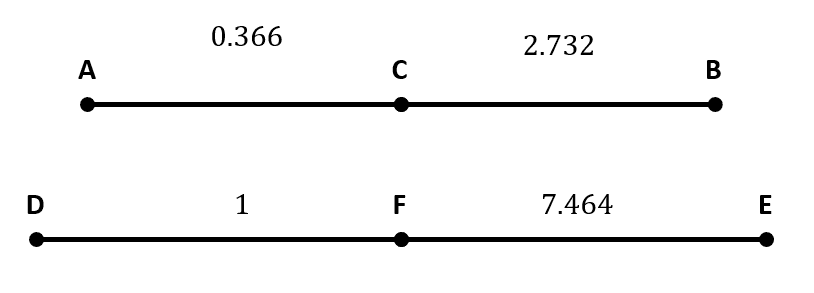
Dados los segmentos de la figura, ¿para qué valores de x se cumple que los segmentos son proporcionales?
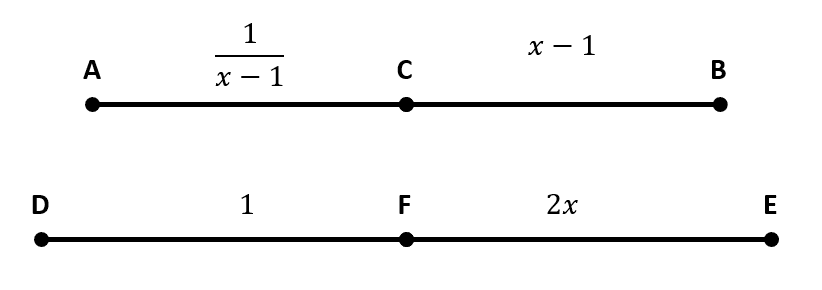
\frac{AC}{CB}=\frac{DF}{FE}
- 3.732
- 0.732
- 0.268
Solución:
En este caso, debemos igualar a las razones que dividen a los segmentos AB y DE . En términos geométricos, el valor de x que encontremos satisface la proporcionalidad entre AB y DE . Una vez resolvamos la ecuación resultante, debemos evaluar los resultados de x cuidando que ningún segmento sea negativo.
\frac{AC}{CB}=\frac{DF}{FE}\to \frac{\frac{1}{x-1}}{x-1}=\frac{1}{2x}\to \frac{1}{{\left(x-1\right)}^{2}}=\frac{1}{2x}
Linealizamos la expresión y desarrollamos el producto notable.
2x={x}^{2}-2x+1\to {x}^{2}-4x+1=0
Debemos resolver la ecuación de segundo grado:
{x}^{2}-4x+1=0
Aplicamos la fórmula de segundo grado para resolver la ecuación.
{x}_{\mathrm{1,2}}=\frac{-\left(-4\right)\pm \sqrt{{\left(-4\right)}^{2}-4\left(1\right)\left(1\right)}}{2\left(1\right)}=\frac{4\pm \sqrt{16-4}}{2}=\frac{4\pm \sqrt{12}}{2}
Los posibles valores para x son:
{x}_{1}=3.732 y {x}_{2}=0.268
Descartamos a {x}_{2} porque arrojaría resultados negativos en los segmentos AC y CB .
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 12
La producción en una empresa de enlatados depende de los registros de demanda para los 5 meses anteriores. En la siguiente tabla se muestran la producción (en rojo) y la demanda (en amarillo) para los 5 meses anteriores.
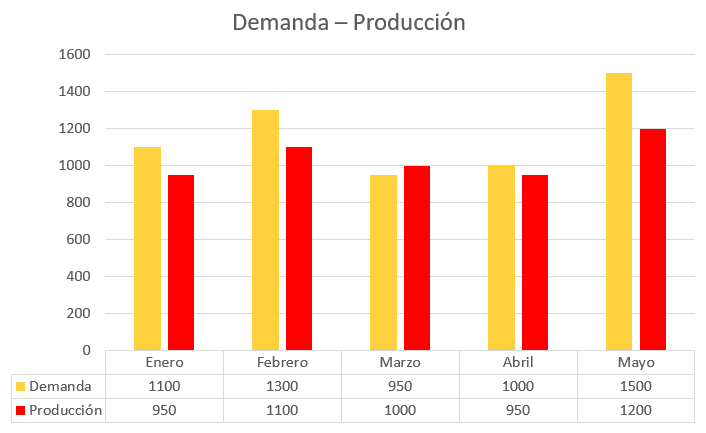
La producción del mes siguiente (junio), se calcula sumando a la producción del mes anterior el promedio de las diferencias \mathrm{d}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{a}-\mathrm{o}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{a} de los meses anteriores. ¿Cuál es la producción para el siguiente mes?
- 1030
- 1330
- 1630
Solución:
Haciendo síntesis de lo indicado por el enunciado, debemos estimar la producción de la empresa para el mes de junio, tomando como base la producción del mes de mayo y sumándole el promedio de las diferencias Demanda – Producción de los meses anteriores.
Iniciamos calculando las respectivas diferencias.
{D}_{1}=1100-950=150
{D}_{2}=1300-1100=200
{D}_{3}=950-1000=-50
{D}_{4}=1000-950=50
{D}_{5}=1500-1200=300
Ahora, calculamos el promedio de las diferencias.
\stackrel{-}{D}=\frac{150+200-50+50+300}{5}=130
Finalmente, la producción para el mes de junio es:
{P}_{6}=1200+130=1330
Concluimos indicando como respuesta correcta al inciso b).
Reactivo 13
Un estudiante necesita llegar lo más rápido posible a su clase de matemáticas, pero la ruta del tren que toma todos los días está congestionada. En su lugar, tiene las dos opciones que se muestran a continuación:
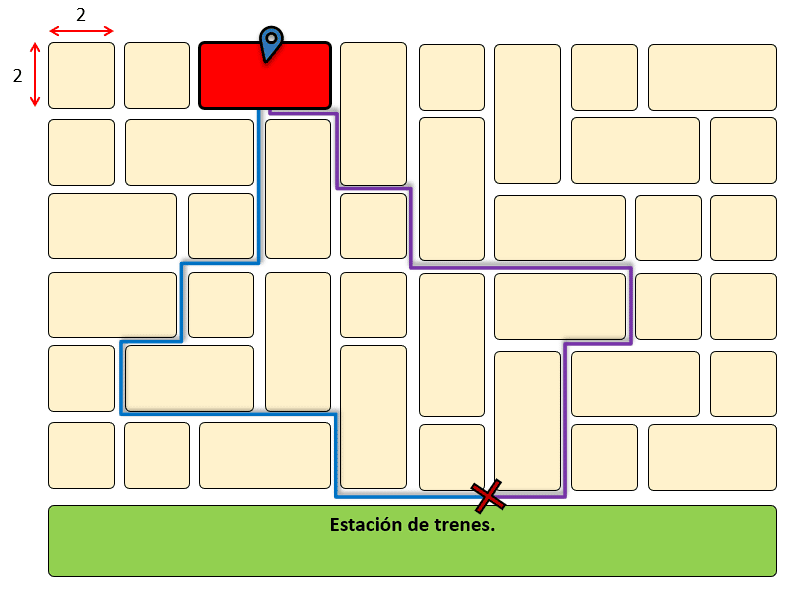
La ruta de color morado se recorre con una rapidez promedio de 10 m/s, mientras que la ruta de color azul se recorre a 8 m/s. ¿Cuál es la ruta más rápida?
- Azul
- Ambas
- Morada
Solución:
Lo primero que debemos calcular es la distancia de ambas rutas, para luego dividir esta longitud por la rapidez promedio correspondiente.
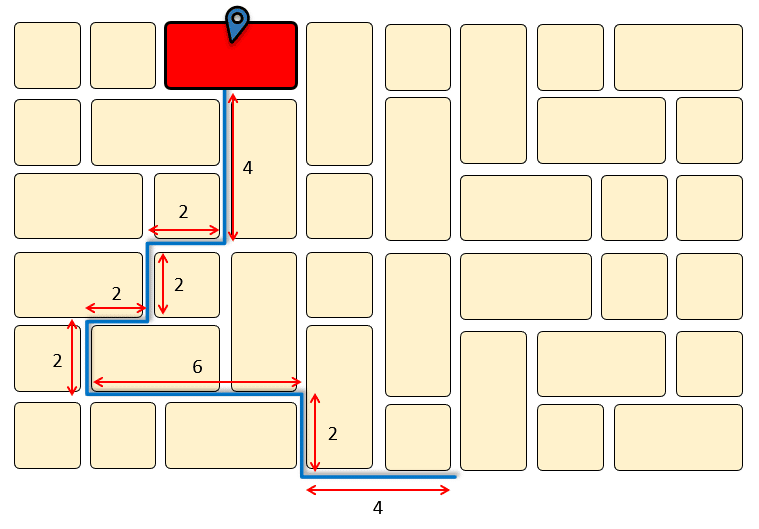
Longitud de la ruta azul.
{R}_{a}=4+2+6+2+2+2+2+4=24 \mathrm{m}
Longitud de la ruta morada.
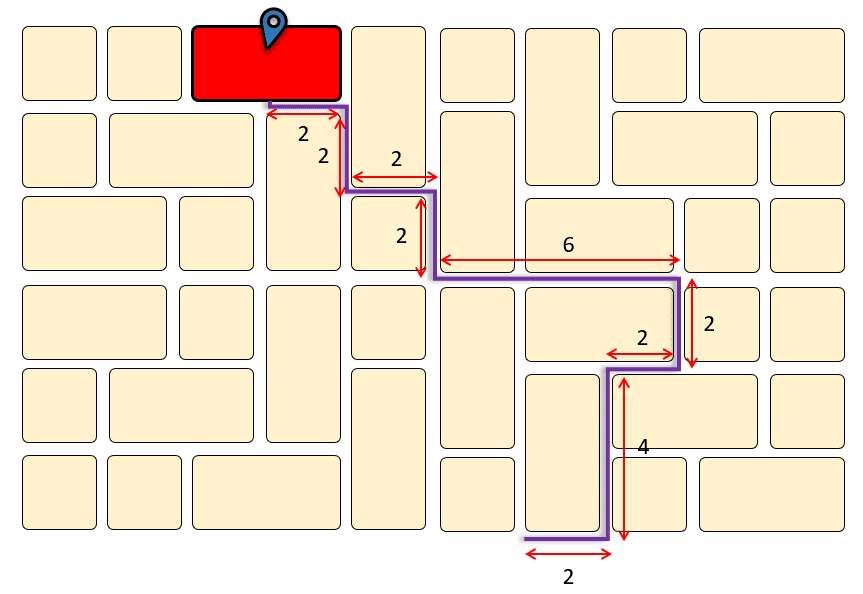
{R}_{m}=2+4+2+2+6+2+2+2+2=24 \mathrm{m}
Debido a que ambas rutas tienen la misma longitud, seleccionamos la que tenga mayor rapidez promedio, es decir, la ruta morada. Concluimos indicando como respuesta correcta al inciso c).
Reactivo 14
Se tiene un juego de azar, en el que hay dos urnas. En la primera hay 3 bolas rojas y 2 amarillas, mientras que en la segunda hay 1 bola roja y 3 amarilla. ¿Cuál es la probabilidad de obtener una bola roja en la primera extracción?
- \frac{4}{9}
- \frac{1}{9}
- \frac{1}{4}
Solución:
Debido a que nos encontramos en la primera extracción, la probabilidad de sacar una bola roja es igual al total de bolas rojas sobre las bolas en ambas urnas. En este caso no hacemos distinción entre las urnas, porque solo nos interesa que el resultado sea una bola roja.
\mathrm{P}\left(\mathrm{B}\mathrm{R}\right)=\frac{3+1}{3+2+1+3}=\frac{4}{9}\approx 0.4444
Hay una probabilidad del 44.44% de sacar una bola roja en la primera extracción.
Concluimos el ejercicio indicando como respuesta correcta al inciso a).
Reactivo 15
Identifique la figura que se forma al otro lado del eje por simetría axial.
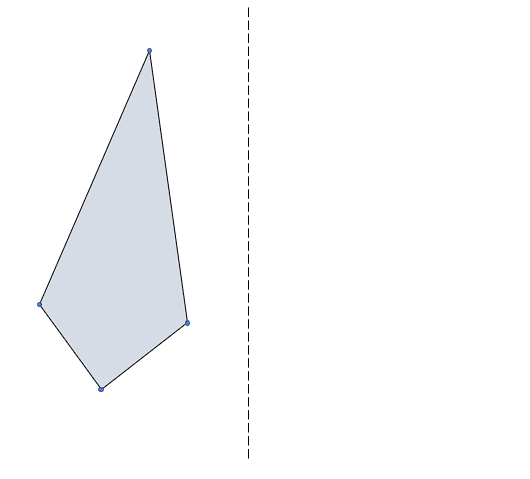
Solución:
En geometría, una figura es simétrica respecto a otra a partir de un eje o de un punto. Se reconocen 3 tipos de simetría básicas: traslacional, central o radial y axial.
Para efectos de este ejercicio, la simetría axial es la reflexión especular de un cuerpo geométrico respecto a un eje de simetría. La figura es el polígono de relleno azul y el eje es la línea negra punteada.
Aplicando la definición de simetría axial, el objeto reflejado es:
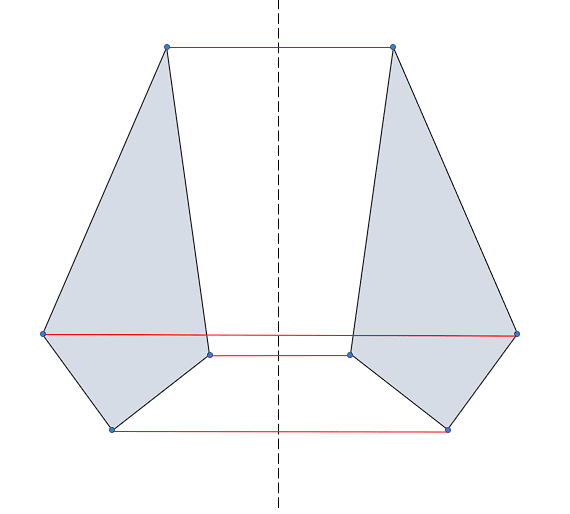
La respuesta correcta es el inciso a).
Reactivo 16
Juan, Emilia y Gabriel van a almorzar a un restaurante y acuerdan pagar la cuenta entre los tres. Juan pide una pizza a las leñas y 1 refresco con un total de 230$. Emilia pide un filete de salmón con ensalada por 320$ y Gabriel pide un corte de res con papas fritas y refresco por 287$.
¿Cuál de los tres amigos termina pagando más dinero respecto al precio de su platillo?
- Emilia
- Juan
- Gabriel
Solución:
Iniciamos calculando el total de la cuenta por los tres platillos.
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}=230+320+287=837\mathrm{\$}
Ahora, dividimos el total entre tres para obtener el monto a pagar por cada uno.
\mathrm{M}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{ }\mathrm{a}\mathrm{ }\mathrm{p}\mathrm{a}\mathrm{g}\mathrm{a}\mathrm{r}=279\mathrm{\$}
Comparando este resultado con el precio de los platillos, concluimos que Juan es quien paga la mayor diferencia, mientras que Emilia es quien sale mejor beneficiada. La respuesta correcta es el inciso b).
Reactivo 17
Complete la siguiente frase utilizando el concepto de regla de tres.
Todas las partes del Simulacro:
Una planta fabrica 300 piezas en 4 horas con 2 máquinas. Si desean aumentar la producción a 780 piezas y el tiempo estimado es de 7 horas, deberán adicionar ______ máquinas a la planta.
- 1
- 2
- 3
Solución:
Una vez analizado el ejercicio, queda claro que debemos emplear una regla de tres compuesta, ya que hay 3 variables en juego: piezas a fabricar, tiempo y número de máquinas. Además, la variable de interés es el número de máquinas.
Organizamos los datos en una tabla los datos suministrados.

Ahora, establecemos las relaciones entre las variables.
Piezas a fabricar – máquinas: si se desean fabricar más piezas, se debe incrementar el número de máquinas. Relación directa.
Tiempo – máquinas: si la planta cuenta con mayor cantidad de máquinas, el tiempo de fabricación será menor. Relación inversa.
Escribimos la igualdad como:
\frac{x}{2}=\left(\frac{780}{300}\right)\left(\frac{4}{7}\right)\to x=2\left(\frac{780}{300}\right)\left(\frac{4}{7}\right)
x=2.971\approx 3
La planta necesita 3 máquinas para suplir la nueva demanda en el tiempo estipulado. Es necesario integrar otra máquina.
Una planta fabrica 300 piezas en 4 horas con 2 máquinas. Si desean aumentar la producción a 780 piezas y el tiempo estimado es de 7 horas, deberán adicionar una máquina a la planta.
Concluimos que la respuesta correcta es el inciso a).
Reactivo 18
Sin utilizar la fórmula de segundo grado, ¿qué valores a y b permiten factorizar el polinomio 3{x}^{2}+3x-6 ?
- a=-1, b=2
- a=-1, b=-2
- a=1, b=1
Solución:
Antes de aplicar la técnica de factorización, debemos extraer como factor común el 3.
3{x}^{2}+3x-6=3\left({x}^{2}+x-2\right)
Ahora, debemos buscar dos números que sumados den +1 y que multiplicados sean -2.
a+b=1, ab=-2
Si probamos con el -1 y el +2 obtenemos:
a+b=-1+2=1
ab=\left(-1\right)\left(2\right)=-2
Factorizamos el trinomio como: \left(x+a\right)\left(x+b\right) .
3\left({x}^{2}+x-2\right)=3\left(x-1\right)\left(x+2\right)
Concluimos el ejercicio indicando como respuesta correcta al inciso a).
Reactivo 19
Desarrolle el siguiente trinomio al cuadrado utilizando el producto notable correcto.
{\left(2x-y+z\right)}^{2}
- 4{x}^{2}+{y}^{2}+{z}^{2}-4xyz
- 4{x}^{2}-{y}^{2}+{z}^{2}-4xy-4xz-2yz
- 4{x}^{2}+{y}^{2}+{z}^{2}-4xy+4xz-2yz
Solución:
Iniciamos agrupando a dos de los términos dentro de la potencia. En nuestro caso elegimos agrupar a 2x con -y .
{\left(\left(2x-y\right)+z\right)}^{2}
Ahora, aplicamos la fórmula del binomio al cuadrado donde a=2x-y y b=z .
{\left(\left(2x-y\right)+z\right)}^{2}={\left(2x-y\right)}^{2}+2z\left(2x-y\right)+{z}^{2}
Desarrollamos el binomio al cuadrado indicado.
{\left(2x-y\right)}^{2}+2z\left(2x-y\right)+{z}^{2}=4{x}^{2}-4xy+{y}^{2}+4xz-2yz+{z}^{2}
Reacomodamos.
4{x}^{2}-4xy+{y}^{2}+4xz-2yz+{z}^{2}=4{x}^{2}+{y}^{2}+{z}^{2}-4xy+4xz-2yz
Finalmente:
{\left(2x-y+z\right)}^{2}=4{x}^{2}+{y}^{2}+{z}^{2}-4xy+4xz-2yz
Comparando con los incisos, indicamos como respuesta correcta al c).
Reactivo 20
En una construcción civil, se necesitan construir dos acueductos: uno de 36 metros y otro de 60 metros. Por temas económicos, la constructora le solicita utilizar la misma longitud de tubería, de tal forma que cubra el mayor tramo posible.
¿Cuántos segmentos de tubería se deben comprar para la construcción?
- 12 segmentos
- 8 segmentos
- 9 segmentos
Solución:
Para encontrar el trozo de tubería de máxima longitud que permite cubrir ambos tramos, es necesario calcular el máximo común divisor entre 36 y 60 metros.
MCD\left(36, 60\right)=12 \mathrm{m}
Se necesitan tuberías de 12 metros para cubrir ambos tramos. Calculamos cuántos se necesitan para toda la construcción.
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}=\frac{36+60}{12}=8 \mathrm{t}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{o}\mathrm{s}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{t}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{í}\mathrm{a}
Se necesitan 8 tramos de 12 metros para construir ambos acueductos.
La respuesta correcta es el inciso b).