Tercera parte del examen simulador de pensamiento del Exani II, vamos a resolver los ejercicios del 21 al 30 y explicarlos paso a paso.

En la sección de materiales podrás encontrar simulacros de otras áreas del examen, durante el curso abarcamos el 100% de los temas del nuevo Exani II.
Estructura del Exani II
El Exani II consta de 168 reactivos y se divide en diferentes módulos, tres de ellos se evocan a evaluar aptitudes de conocimiento general, y otros dos son de conocimiento específico y varían según la carrera a la que apliques.
Para que conozcas mejor su estructura, consulta la siguiente tabla:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Temario de Pensamiento matemático
Pensamiento Matemático es probablemente la parte más difícil del examen dentro de la sección de conocimientos generales, donde tendrás que resolver 30 reactivos. A continuación te mostramos el temario completo de áreas que se evalúan en esta parte del Exani II:
Subárea: Comprensión de lo matemático
- Sentido numérico
- Inecuaciones lineales
- Simplificación de expresiones algebraicas
- Razones trigonométricas
- Área
- Desviación estándar
- Media aritmética
- Conexiones
- Razones y proporciones
- Interpretación gráfica de ecuaciones lineales
- Ejes de simetría
- Estimación de trayectorias
- Frecuencias
- Probabilidad clásica de eventos simples
- Estimaciones
- Leyes de los exponentes
- Porcentaje
- Unidades de medida como patrón de comparación
- Espacio muestral
Subárea: Matematización
- Desarrollo de usos
- Representación gráfica de ecuaciones de segundo grado
- Comportamiento gráfico de funciones cuadráticas
- Relaciones trigonométricas
- Representación gráfica de información
- Medidas de tendencia central y de dispersión
- Lenguaje matemático
- Polinomios
- Sistemas de ecuaciones lineales con dos y tres incógnitas
- Resignificaciones
- Variación lineal tabular
- Medidas de posición (deciles, cuartiles y percentiles)
Si bien matemáticas suele ser la materia que se considera más difícil, toma en cuenta que en tu examen vendrán 30 reactivos de los 138, por lo que es igual de importante estudiar español, así como los módulos específicos.
Reactivo 21
¿Cuál es el área de la figura que se muestra en la figura?
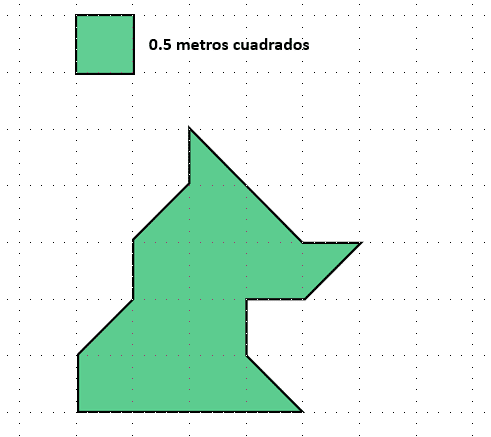
- 8 metros cuadrados
- 4 metros cuadrados
- 6 metros cuadrados
Solución:
Para encontrar el área de la figura irregular, debemos divisar en ella cuadrados o fracciones de cuadrados que correspondan al que tiene por área 0.5 {\mathrm{m}}^{2} . Iniciamos identificando los cuadrados completos dentro de la figura.
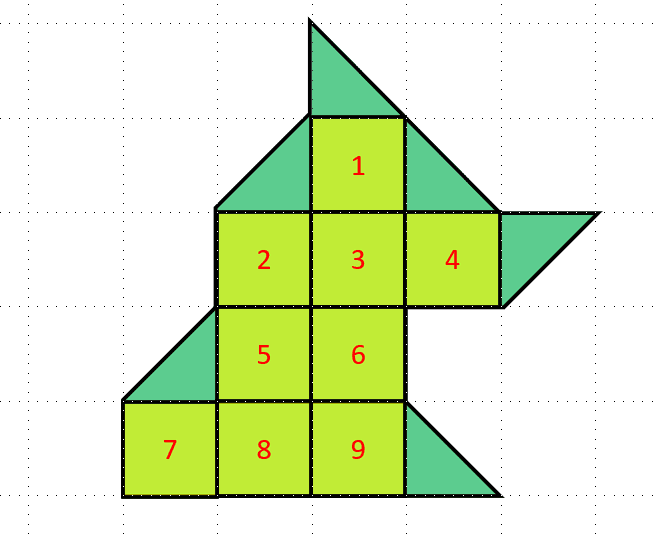
Tenemos un total de 9 cuadrados. Por otra parte, en la figura hay también triángulos, correspondientes a la mitad de un cuadrado. En total, hay 6 medios cuadrados. El área total de la figura se puede calcular como:
{A}_{f}=9{A}_{c}+6{A}_{t}
Si el área de los triángulos es la de medio cuadrado:
{A}_{t}=\frac{{A}_{c}}{2}
Sustituimos en la primera expresión.
{A}_{f}=9{A}_{c}+\frac{6{A}_{c}}{2}=12{A}_{c}
Finalmente:
{A}_{f}=12\left(0.5\right)=6 {\mathrm{m}}^{2}
La figura tiene un área de 6 metros cuadrados.
Concluimos el ejercicio indicando como respuesta correcta al inciso c).
Reactivo 22
Dados los polinomios 3{x}^{5}-{x}^{4}+2{x}^{3}-{x}^{2}+3 y {x}^{3}+{x}^{2}-x+1 , calcule el resto de su división.
- 3{x}^{2}-4x+9
- -17{x}^{2}+13x-6
- {x}^{3}+{x}^{2}-x+1
Solución:
Emplearemos el algoritmo de la división sintética. Iniciamos disponiendo a los polinomios de la siguiente forma:
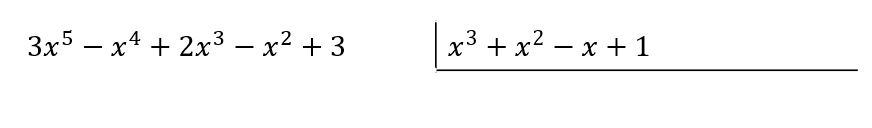
Recordemos que el algoritmo para la división es el siguiente:
- Encontramos un monomio que, multiplicado por el término de mayor grado del divisor, sea igual al término de mayor grado en el dividendo.
- El monomio que se obtiene de la multiplicación se escribe con el signo cambiado.
Teniendo en cuenta lo anterior, para eliminar a 3{x}^{5} debemos multiplicar a {x}^{3} por 3{x}^{2} .
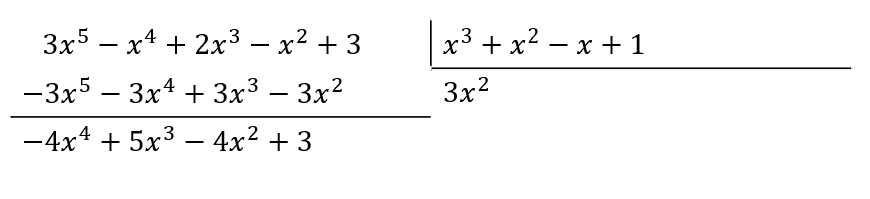
Ahora, multiplicamos por -4x al divisor.
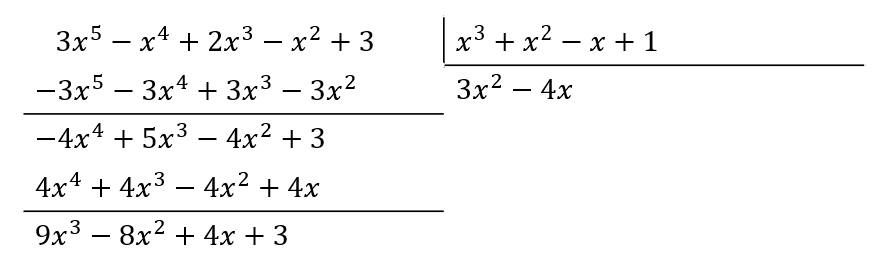
Finalmente, multiplicamos el divisor por 9.
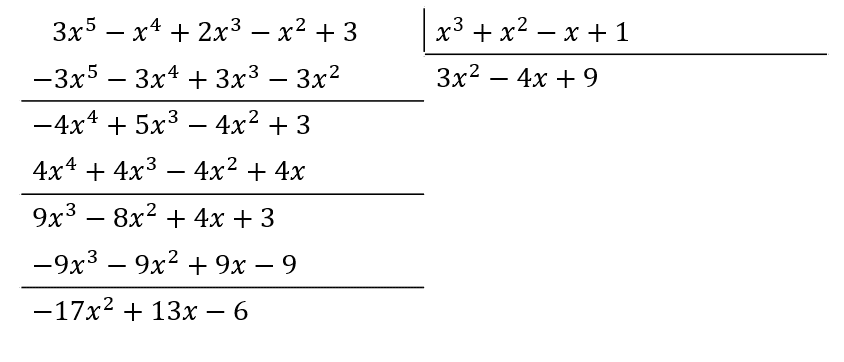
Reescribimos el resultado del cociente de los polinomios como:
\frac{3{x}^{5}-{x}^{4}+2{x}^{3}-{x}^{2}+3}{{x}^{3}+{x}^{2}-x+1}=3{x}^{2}-4x+9+\frac{-17{x}^{2}+13x-6}{{x}^{3}+{x}^{2}-x+1}
El residuo del cociente es: -17{x}^{2}+13x-6 .
Concluimos el ejercicio seleccionando como respuesta correcta al inciso b).
Reactivo 23
En un experimento aleatorio, se tienen dos cajas. Una de ellas con 3 canicas rojas y 2 azules, mientras que la segunda tiene 2 canicas rojas y 2 azules. Calcule la probabilidad de extraer una canica azul.
- 0.45
- 0.4
- 0.5
Solución:
Para resolver este problema, vamos a iniciar trazando el diagrama de árbol para el experimento. De esta forma, tendremos una visión clara de lo que sucede en la extracción.
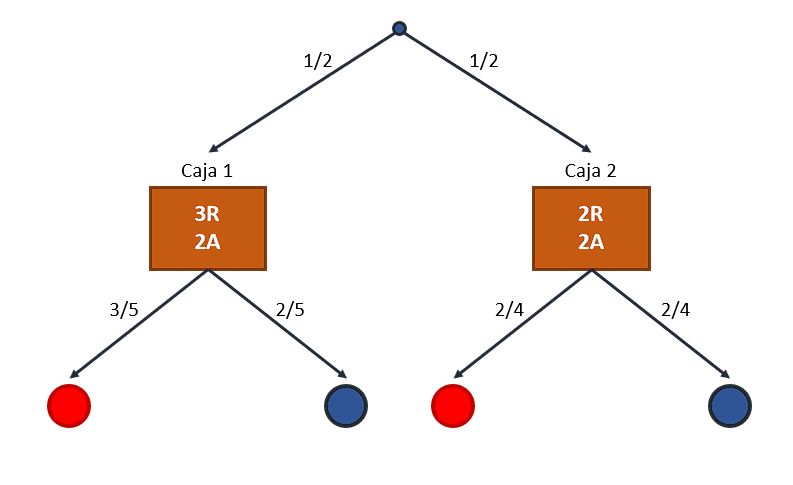
A partir del diagrama, identificamos que primero hay que escoger una de las dos cajas, por ello, las primeras dos ramas tienen el valor de ½ . Ahora, a través de estas ramas debemos descender por las que nos lleven a seleccionar una canica azul en ambas cajas.
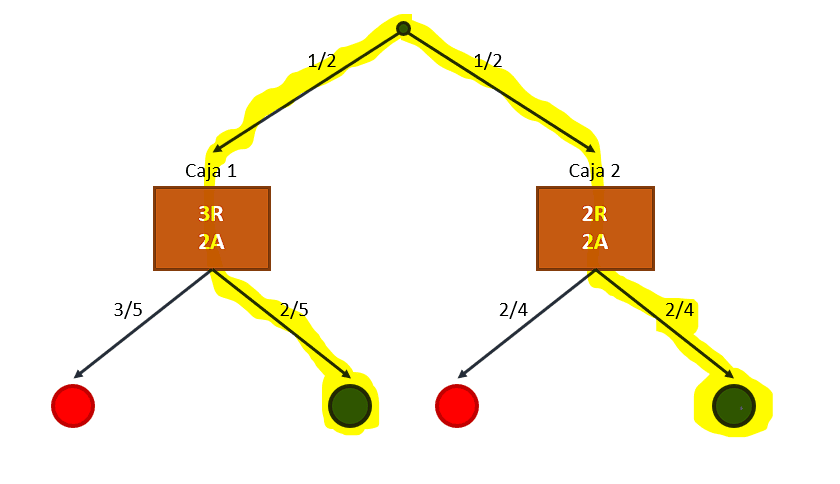
De esta forma, la probabilidad de escoger una bola azul es igual a la suma de la probabilidad de escoger una azul de la caja 1 más la probabilidad de escoger una azul de la caja 2.
P\left(A\right)=P\left(1\right)P\left(A/1\right)+P\left(2\right)P\left(A/2\right)
Sustituimos los valores correspondientes.
P\left(A\right)=\left(\frac{1}{2}\right)\left(\frac{2}{5}\right)+\left(\frac{1}{2}\right)\left(\frac{2}{4}\right)=0.45
La respuesta correcta es el inciso a).
Reactivo 24
¿Cuál es la solución de la siguiente inecuación?
\frac{1}{2x-1}>0
- x\in \left(\frac{1}{2}, \infty \right)
- x\in \left(\infty , \frac{1}{2}\right)
- x\in \left(-\frac{1}{2}, \infty \right)
Solución:
Para resolver esta inecuación, no podemos aplicar un simple despeje debido a que la variable se encuentra en el denominador de la fracción. En su lugar, es necesario aplicar un estudio de signos a la fracción.
El símbolo de la inecuación nos marca que \frac{1}{2x-1} debe ser mayor que cero, es decir, positivo. Para que esto ocurra en una fracción, el numerador y el denominador deben ser positivos o negativos a la vez.
Debido a que el numerador es una constante positiva +1, esto nos deja una única posibilidad para el denominador: que sea también positivo.
\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{ }\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{ }\frac{1}{2x-1}>0, 2x-1>0
Luego de este sencillo análisis, solo nos queda despejar el conjunto solución de x .
2x-1>0\to 2x>1\to x>\frac{1}{2}
Para que la fracción \frac{1}{2x-1} sea mayor que cero, x debe ser mayor que ½.
x\in \left(\frac{1}{2}, \infty \right)
Concluimos el ejercicio indicando como respuesta correcta al inciso a).
Reactivo 25
A partir de las curvas que se muestran a continuación, ¿cuáles son sus puntos de intercepción?
{x}^{2}+y=1
y=x-1
- {P}_{1}\left(-\mathrm{1,0}\right), {P}_{2}\left(2, -3\right)
- {P}_{1}\left(1, 2\right), {P}_{2}\left(-1, -2\right)
- {P}_{1}\left(\mathrm{1,0}\right), {P}_{2}\left(-2, -3\right)
Solución:
Para determinar los puntos de intersección, es necesario resolver el sistema de ecuaciones que forman ambas curvas.
\left\{\begin{array}{c}{x}^{2}+y=1\\ y=x-1\end{array}\right.
Debido a que el sistema no es lineal, debemos aplicar sustitución. Debido a que la segunda expresión tiene a la y despejada, simplemente sustituimos el otro lado de la igualdad en la primera ecuación.
{x}^{2}+\left(x-1\right)=1\to {x}^{2}+x-2=0
Las raíces del trinomio se obtienen fácilmente con el método de factorización correspondiente. Debemos hallar dos números que multiplicados sean -2 y que sumados 1.
a=-1, b=2
-1+2=1, \left(-1\right)\left(2\right)=-2
{x}^{2}+x-2=\left(x-1\right)\left(x+2\right)
Despejando a las raíces obtenemos:
{x}_{1}=1, {x}_{2}=-2
Sustituimos estos valores en la segunda ecuación para obtener los valores de y .
{y}_{1}=1-1=0
{y}_{2}=-2-1=-3
Finalmente, los puntos de intersección son:
{P}_{1}\left(\mathrm{1,0}\right), {P}_{2}\left(-2, -3\right)
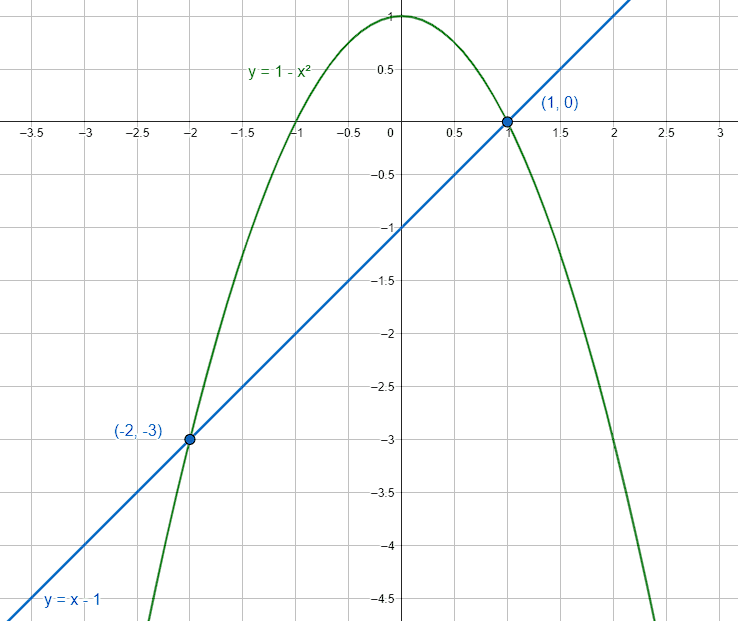
La respuesta correcta es el inciso c).
Reactivo 26
Se tiene un experimento aleatorio en el que se lanzan 2 dados de 6 caras. Calcule la probabilidad de que la suma de las caras sea mayor o igual que 6.
- \frac{13}{18}
- \frac{1}{16}
- \frac{1}{6}
Solución:
A partir de los dos dados, se pueden obtener 36 resultados diferentes.
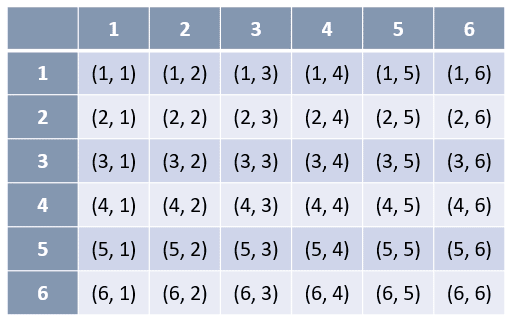
Partiendo de la anterior tabla de posibles resultados, señalamos aquellos cuya suma sea mayor o igual que 6.
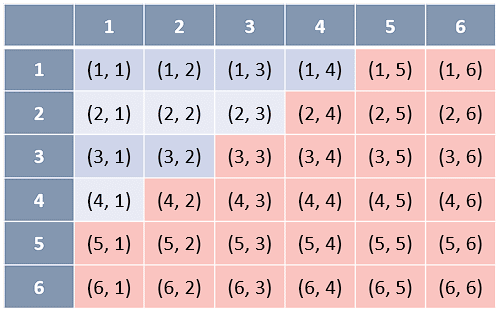
Tenemos 26 posibles pares de resultados cuya suma es mayor o igual que 6. La probabilidad se calcula como:
P\left(\ge 6\right)=\frac{26}{36}=\frac{13}{18}
La probabilidad de lanzar ambos dados y que los números en sus caras sumen más o igual que 6 es \frac{13}{18}\approx 0.722 .
Concluimos el ejercicio indicando como respuesta correcta al inciso a).
Todas las partes del Simulacro:
Reactivo 27
Dadas las ecuaciones que se muestran a continuación, ¿qué puede concluir acerca de sus soluciones sin realizar ningún cálculo?
\left\{\begin{array}{c}3x-y=1\\ -6x+2y=-2\end{array}\right.
- Tiene infinitas soluciones
- No tiene ninguna solución
- Tiene una única solución
Solución:
Si dividimos a la segunda ecuación por -2, encontramos que ambas ecuaciones son equivalentes.
-6x+2y=-2\to 3x-y=1
Esto quiere decir que tenemos un sistema con la misma ecuación repetida dos veces. Como consecuencia de esto, hay infinitas soluciones para el sistema ya que todos los puntos de {E}_{1} pertenecen a {E}_{2} .
Examinando los incisos y teniendo en cuenta todo lo anterior, concluimos que la respuesta correcta es el inciso a).
Reactivo 28
¿Cuál es el valor de \mathrm{sec}x , si se tiene que \mathrm{t}\mathrm{g}x=\frac{1}{2} ?
- \frac{2}{\sqrt{5}}
- \frac{\sqrt{5}}{2}
- \frac{\sqrt{3}}{2}
Solución:
Este problema puede resolverse de dos formas: empleando la relación trigonométrica entre la secante y la tangente o, recurriendo a un triángulo rectángulo. Debido a que la primera opción es más rápida, será esa nuestra herramienta de solución.
Identidad pitagórica en términos de la secante y la tangente.
{\mathrm{tan}}^{2}x+1={\mathrm{sec}}^{2}x
Aplicamos raíz cuadrada de ambos lados. Nos quedamos solo con la parte positiva de la raíz.
\mathrm{sec}x=\sqrt{{\mathrm{tan}}^{2}x+1}=\sqrt{{\left(\frac{1}{2}\right)}^{2}+1}=\sqrt{\frac{1}{4}+1}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2}
Finalmente:
\mathrm{tg}x=\frac{1}{2}\to \mathrm{sec}x=\frac{\sqrt{5}}{2}
La respuesta correcta al ejercicio es el inciso b).
Reactivo 29
¿Para qué valores se anula la secante de un ángulo alfa?
- Ninguno
- n\pi
- n\pi +\frac{\pi }{2}
Solución:
Iniciemos recordando a que es igual la secante de un ángulo.
\mathrm{sec}\alpha =\frac{1}{\mathrm{cos}\alpha }
Para que el cociente anterior llega a anularse, necesitaríamos que el numerador valga cero. Eso último no es posible porque el numerador es una constante. Con este sencillo análisis, concluimos que la secante de alfa no se anula para ningún valor.
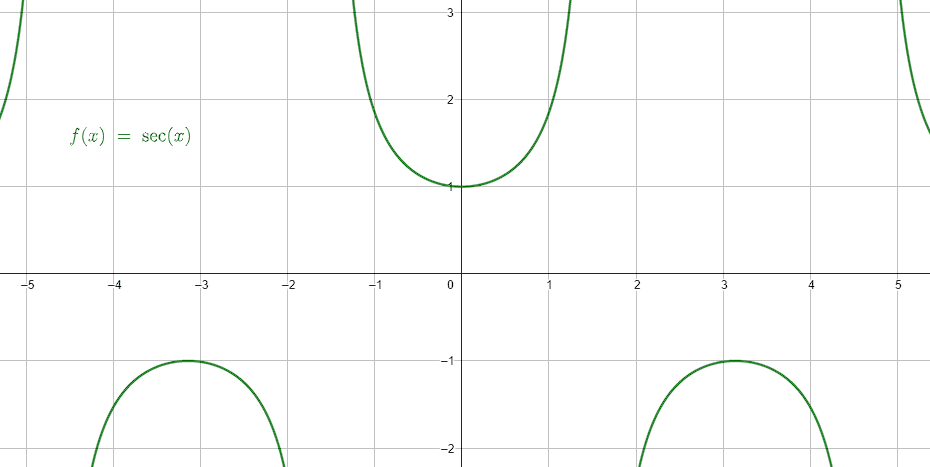
Concluimos que la respuesta correcta es el inciso a).
Reactivo 30
¿A qué valor tiende la cotangente cuando el ángulo \alpha tiende a cero?
- indeterminado
- 0
- 1
Solución:
Para resolver este problema, debemos recordar qué es igual la cotangente del ángulo.
\mathrm{cot}\alpha =\frac{\mathrm{cos}\alpha }{\mathrm{sin}\alpha }
Cuando el ángulo \alpha tiende a cero, el coseno es igual a 1 y el seno es igual a cero.
\mathrm{cot}\alpha =\frac{1}{0}
Al tener este cociente, decimos que la cotangente se indetermina cuando \alpha es cero.
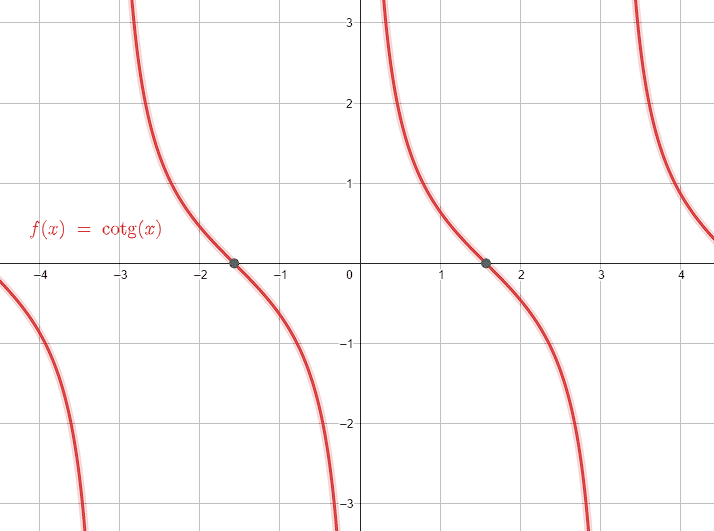
Examinando los incisos, concluimos que la respuesta correcta es el a).


