Con este tutorial iniciamos la solución de la tercera versión del examen simulacro de temas de la Guía EXANI II de pensamiento matemático. Vamos a resolver la primera parte de la tercera versión, que va desde el reactivo 1 hasta el 10.

Pensamiento matemático mezcla temas como aritmética, álgebra y probabilidad y estadística. Te recomiendo repasar el temario antes de pasar con los ejercicios.
Estructura del EXANI II
El EXANI II se compone por dos grandes partes: una de habilidades y conocimientos y otra con los módulos específicos.
Adicionalmente, algunas universidades aplican un examen diagnóstico de inglés, que no cuenta para la calificación final. Debes consultar esta información en la convocatoria de tu universidad.
Examen de habilidades y conocimientos
La parte habilidades y conocimientos aplica para todas las carreras. Esta se compone de 90 reactivos: 60 de Español y 30 de Matemáticas. En la siguiente tabla se encuentra la distribución de los reactivos del EXANI II.
Estructura del examen y la guía del EXANI II
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
Conocimientos específicos del EXANI II posee un total de 15 módulos. Todos los estudiantes deben responder 2 módulos en esta segunda parte, los cuales varían de acuerdo con la carrera.
Es necesario que revises la convocatoria de tu universidad para conocer qué módulos van para tu examen. A continuación, te dejo una lista con los módulos específicos del EXANI II.
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Pensamiento Matemático EXANI II
En la siguiente tabla te mostramos la distribución de los 30 reactivos de pensamiento matemático y los temas que van para el examen.
| Contenido | Reactivos |
|---|---|
| Herramientas Algebraicas: Resolución de problemas mediante el empleo de ecuaciones y sistemas lineales, ya sea a través de la representación de cantidades o de la representación gráfica | 10 |
| Problemas, Probabilidad y Análisis de Datos: Creación y análisis de relaciones, representación y análisis de datos cuantitativos y aplicación de probabilidades | 15 |
| Matemáticas Avanzadas: Creación de expresiones algebraicas y uso de gráficos que representan funciones exponenciales no lineales o cuadráticas | 15 |
| Temas Adicionales en Matemáticas: Solución de problemas asociados al área y volumen, aplicación de definiciones, teoremas sobre líneas, ángulos, triángulos y círculos | 10 |
| Total | 50 |
Algunos temas específicos son:
- Inecuaciones lineales
- Simplificación de expresiones algebraicas
- Razones trigonométricas
- Área
- Desviación estándar
- Media aritmética
- Razones y proporciones
- Interpretación gráfica de ecuaciones lineales
- Ejes de simetría
- Estimación de trayectorias
- Frecuencias
- Probabilidad clásica de eventos simples
- Leyes de los exponentes
- Porcentaje
- Unidades de medida como patrón de comparación
- Espacio muestral
- Representación gráfica de ecuaciones de segundo grado
- Comportamiento gráfico de funciones cuadráticas
- Relaciones trigonométricas
- Representación gráfica de información
- Medidas de tendencia central y de dispersión
- Polinomios
- Sistemas de ecuaciones lineales con dos y tres incógnitas
- Variación lineal tabular
- Medidas de posición (deciles, cuartiles y percentiles)
Recomendaciones para resolver la guía
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
Se tiene una hoja de papel bond con un ancho de 20 cm. Si la esquina derecha se dobla encima del pliego de hoja con un ángulo \theta , tal como se muestra en la figura, determine:
- La longitud L del doblez hecho
- Si el ángulo del doblez es \theta =30° y \mathrm{sin}30°=\frac{1}{2} , ¿cuánto ha de valer L ?
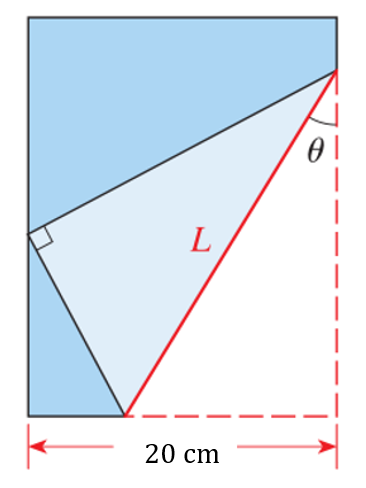
- L=\frac{10}{\mathrm{s}\mathrm{e}\mathrm{n}\theta {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta }, L=26.6
- L=\frac{3}{\mathrm{s}\mathrm{e}\mathrm{n}\theta {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta }, L=8
- L=\frac{15}{\mathrm{s}\mathrm{e}\mathrm{n}\theta {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta }, L=40
Solución:
Para resolver este problema, debemos aplicar trigonometría de forma inteligente para evitar trabajar demasiado con las expresiones. Lo primero que debemos identificar es que el triangulo que se forma por la línea punteada es el mismo que el de color azul claro.
Por otra parte, la suma de la base del triángulo azul más chico x y la base del triángulo punteado y es igual al ancho de la hoja, por ahora la llamaremos a .
x+y=a
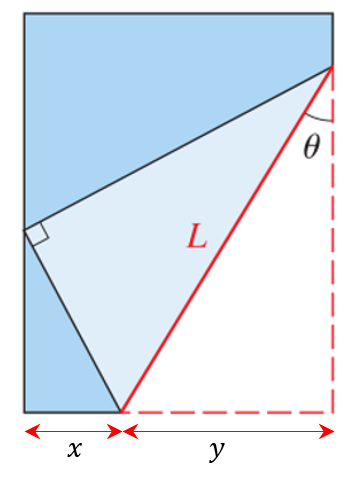
La longitud L se puede calcular como:
\mathrm{sin}\theta =\frac{y}{L}
Pero no conocemos a y , por lo que tendremos que emplear el triangulo chico para determinar su valor.
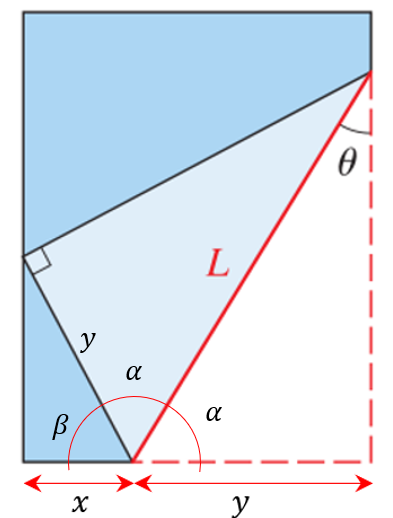
De esta manera, podemos expresar a x como:
\mathrm{cos}\beta =\frac{x}{y}
Ahora, \beta =180-2\alpha . Además, \alpha =90-\theta . Entonces:
\beta =180-2\left(90-\theta \right)=180-180+2\theta
\beta =2\theta
\mathrm{cos}2\theta =\frac{x}{y}
Despejamos a x y la sustituimos en x+y=a .
x=y\mathrm{cos}2\theta
y\mathrm{cos}2\theta +y=a
y=\frac{a}{\mathrm{cos}2\theta +1}
Aplicamos la identidad:
y=\frac{a}{2{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta -1+1}=\frac{a}{2{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta }
Finalmente:
\mathrm{sin}\theta =\frac{a}{2L{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta }\to L=\frac{a}{2\mathrm{sin}\theta {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta }
Sustituimos a=20 .
L=\frac{20}{2\mathrm{sin}\theta {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta }
\therefore L=\frac{10}{\mathrm{sin}\theta {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta }
Debido a que solo conocemos el valor de \mathrm{sin}30 , dejamos al coseno en función del seno.
{\mathrm{sin}}^{2}\theta +{\mathrm{cos}}^{2}\theta =1
L=\frac{10}{\mathrm{sin}\theta \left(1-{\mathrm{sin}}^{2}\theta \right)}
Sustituimos el valor de \mathrm{sin}30 .
L=\frac{10}{\left(\frac{1}{2}\right)\left(1-\frac{1}{4}\right)}=26.6
Indicamos entonces que:
L=\frac{10}{\mathrm{sin}\theta {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\theta } y para \theta =30° L=26.6
Concluimos entonces que la respuesta correcta es la a).
Reactivo 2
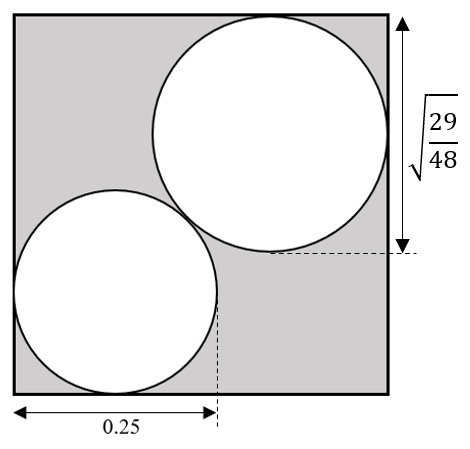
Teniendo en cuenta que la figura mostrada es un cuadrado de lado a=1 , calcule el valor del área sombreada.
- \frac{1}{6}\pi
- 1-\frac{1}{6}\pi
- 1-\pi
Solución:
Para calcular el área sombreada, debemos calcular el área de los círculos y restársela al área del cuadrado.
{A}_{s}={A}_{c}-{A}_{c1}-{A}_{c2}
El problema nos da el diámetro de ambos círculos, por lo que emplearemos la siguiente ecuación para determinar sus áreas.
{A}_{cir}=\frac{\pi {D}^{2}}{4}
{A}_{s}=1-\frac{\pi {D}_{1}^{2}}{4}-\frac{\pi {D}_{2}^{2}}{4}
Tengamos en cuenta que:
{D}_{1}=0.25 y {D}_{2}=\sqrt{\frac{29}{48}}
Sustituimos.
{A}_{s}=1-\frac{\pi {\left(\frac{1}{4}\right)}^{2}}{4}-\frac{\pi {\left(\sqrt{\frac{29}{48}}\right)}^{2}}{4}
Resolviendo y simplificando:
{A}_{s}=1-\frac{\pi }{64}-\frac{29\pi }{192}
{A}_{s}=1-\frac{\pi }{6}
Comparando con las opciones, la respuesta correcta es la b).
Reactivo 3
Encuentre la forma equivalente a la siguiente expresión algebraica.
{\left(1+\frac{1}{x}\right)}^{2}-{\left(1-\frac{1}{x}\right)}^{2}
- \frac{1}{x}-1
- \frac{4}{x}
- \frac{x}{x-1}
Solución:
En este caso, debemos aplicar álgebra para desarrollar los binomios cuadrados, restar y finalmente simplificar. Comencemos por aplicar el producto notable del tipo:
{\left(a\pm b\right)}^{2}={a}^{2}\pm 2ab+{b}^{2}
La expresión quedaría como:
{\left(1+\frac{1}{x}\right)}^{2}-{\left(1-\frac{1}{x}\right)}^{2}=1+\frac{2}{x}+\frac{1}{{x}^{2}}-\left(1-\frac{2}{x}+\frac{1}{{x}^{2}}\right)
1+\frac{2}{x}+\frac{1}{{x}^{2}}-1+\frac{2}{x}-\frac{1}{{x}^{2}}=\frac{4}{x}
Comparando con las opciones, indicamos como correcta la b).
Reactivo 4
Un conductor va en el carril rápido de una autopista y su auto le indica que debe mantener una velocidad menor a 100km/h pero mayor o igual a 80km/h , ya que de ser menor deberá pasar al carril lento de la autopista. ¿Cómo se expresaría en notación de intervalo la situación anterior?
- v\to \left[80, 100\right]
- v\to \left(80, 100\right)
- v\to \left[80, 100\right)
Solución:
Debemos identificar como nos presentan las condiciones en el enunciado. Cuando se refiere a que la velocidad debe ser menor a 100km/h es porque no debe ser igual ni superior a dicha cantidad. Esto se representa como:
v<100
Por otra parte, que la velocidad deba ser mayor o igual a 80km/h es que puede ser igual pero nunca menor. Uniendo esto con la representación anterior, tenemos que la velocidad puede ser 80 o mayor a 80 pero manteniéndose por debajo de 100.
80\le v<100
En notación de intervalo quedaría:
v\to \left[80, 100\right)
Comparando con las opciones, la correcta sería la c).
Reactivo 5
En el gráfico de cualquier mercado, ¿Cuándo ocurre el equilibrio, teniendo en cuenta las curvas de oferta y demanda de un producto?
- Cuanto la cantidad ofertada supera a la cantidad demandada
- Cuando la cantidad demandada supera a la cantidad ofertada
- Cuando la cantidad de oferta y demanda es igual
Solución:
El equilibrio de mercado, por definición, es la intersección entre las curvas de oferta y demanda relacionados a un producto o a un mercado. Teniendo en cuenta las opciones del enunciado, la única que corresponde con lo dicho antes es la c).
Reactivo 6
Existen dos grupos de niños a los que se les midió el peso y se contabilizo en dos tablas separadas. La media obtenida para ambos conjuntos fue de 20 kg. Si los pesos del primer grupo se encontraban cercanos a la media y los del segundo alejados tanto hacia arriba como hacia abajo, ¿Cuál de las siguientes aseveraciones es correcta?
- La desviación del primer grupo es mayor que la desviación del primero
- La desviación es igual porque las medias son iguales
- La desviación del primer grupo es menor que la desviación del segundo
Solución:
Como sabemos, las medidas de dispersión como el rango, la varianza y la desviación típica, miden el nivel de separación que tienen los datos respecto de la media. Por simple razonamiento, si un conjunto de datos está mas cerca de la media, la desviación, rango y varianza serán menores que otro conjunto de datos con mayor dispersión.
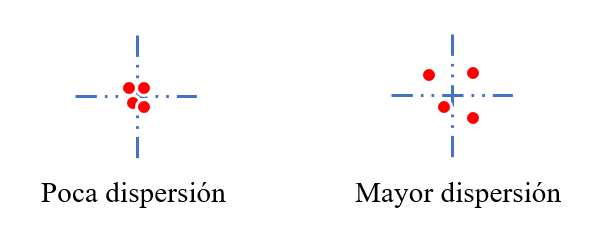
Considerando lo anterior, los pesos del primer grupo de niños cercano a la media tienen una menor desviación que el segundo grupo. Concluimos que la respuesta correcta es la opción c).
Reactivo 7
Relacione el parámetro estadístico de media aritmética con el conjunto al que le corresponde.
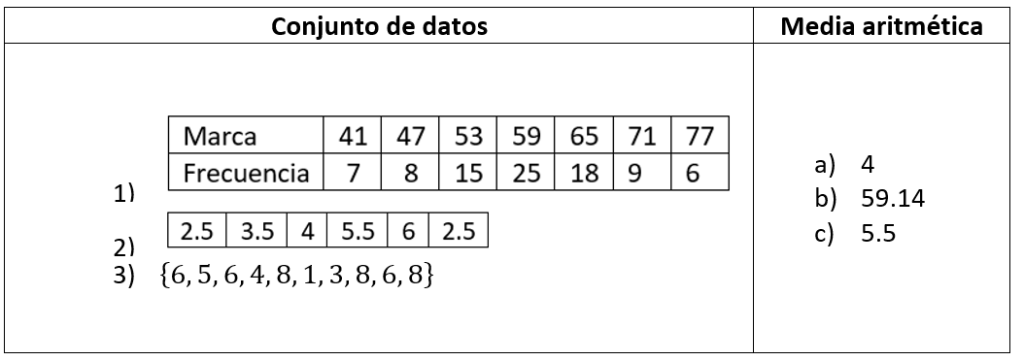
- 1a, 2b, 3c
- 1b, 2a, 3c
- 1c, 2b, 3b
Solución:
Calculamos la media aritmética de cada conjunto de datos y luego la relacionamos con uno de los valores en la columna derecha.
Conjunto de datos 1.
Este primer conjunto corresponde a datos agrupados, por tanto, la fórmula para calcular la media es la suma de los productos de las marcas de clase por la frecuencia de dicha clase.
\stackrel{-}{x}=\frac{\sum xf}{n}
Donde f es la frecuencia, x es la marca y n la frecuencia acumulada total del conjunto de datos.
\stackrel{-}{x}=\frac{41*7+47*8+53*15+59*25+65*18+71*9+77*6}{88}=59.14
Comparando con la columna derecha indicamos que:
1b.
Conjunto de datos 2.
En este caso, se usa la fórmula de media aritmética conocida.
\stackrel{-}{x}=\frac{\sum x}{n}
Sustituimos.
\stackrel{-}{x}=\frac{2.5+3.5+4+5.5+6+2.5}{6}=4
Comparando nos queda:
2a.
Conjunto de datos 3.
Por descartes, es claro que la media de este conjunto es la que se muestra en el inciso c, pero realicemos el cálculo para corroborar.
\stackrel{-}{x}=\frac{\sum x}{n}
Sustituimos.
\stackrel{-}{x}=\frac{6+5+6+4+8+1+3+8+6+8}{10}=5.5
3c.
Concluimos que la respuesta correcta es la b).
Reactivo 8
Como se muestra en la figura, los puntos A , B y C , son colineales y consecutivos. Además, el segmento AB=\frac{AC}{3} . Calcule la longitud del segmento BC , teniendo en cuenta los datos que se muestran en la figura.
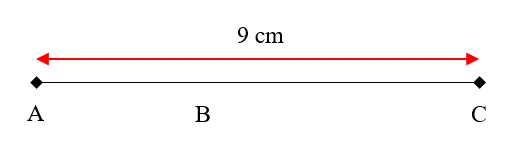
- BC=3
- BC=1
- BC=6
Solución:
En este tipo de problemas con segmentos de recta, debemos establecer un conjunto de ecuaciones que nos permita calcular el valor solicitado. Comencemos indicando que la suma de los segmentos AB y BC es 9, tal como se aprecia en la imagen.
AB+BC=9
Además, la relación AB=\frac{AC}{3} nos dice directamente cuánto vale AB ya que AC=9 .
AB=\frac{9}{3}=3
Sustituimos en la primera ecuación y despejamos.
3+BC=9\to BC=9-3=6
Finalmente:
BC=6 \mathrm{c}\mathrm{m}
Comparando con las opciones, la respuesta correcta es la c).
Reactivo 9
El ayuntamiento de Baja California Sur, en México está desarrollando un estudio estadístico sobre la tendencia de sus ciudadanos a pagar las multas. En la siguiente tabla se encuentran contrastadas las multas emitidas y las multas pagas en los 5 municipios de Baja California Sur durante el mes pasado.

¿Cuál es el municipio con el menor porcentaje de multas sin pagar en toda Baja California Sur?
- Mulegé
- La Paz
- Comondú
Solución:
En este caso, debemos calcular el porcentaje de multas sin pagar que tiene cada municipio de Baja California Sur. Debemos identificar que la tabla nos da la cantidad de multas pagas y el total de multas. Las multas no pagas se calculan como el total menos las que se pagaron.
Comondú.
MNP=105-80=25
{\%}_{1}=\frac{25}{105}*100=23.8
Mugelé.
MNP=70-60=10
{\%}_{2}=\frac{10}{70}*100=14.28
La Paz.
MNP=88-50=33
{\%}_{3}=\frac{38}{88}*100=43.18
Los Cabos.
MNP=33-28=25
{\%}_{4}=\frac{5}{33}*100=15.15
Loreto.
MNP=12-6=6
{\%}_{5}=\frac{6}{12}*100=50
El municipio con menor porcentaje de multas es Mugelé con 14.28%. Comparando con las opciones, el inciso correcto sería el a).
Reactivo 10
A partir del sistema de coordenadas que se muestra en la figura, siga las instrucciones para desplazarse y encuentre la posición en el punto final.
- Desde el punto inicial A recorra 6 cuadros al norte
- Recorra 2 cuadros al oeste y luego 1 al sur
- De nuevo dos cuadros al oeste
- Llegue al punto final B avanzando 3 cuadros al sur
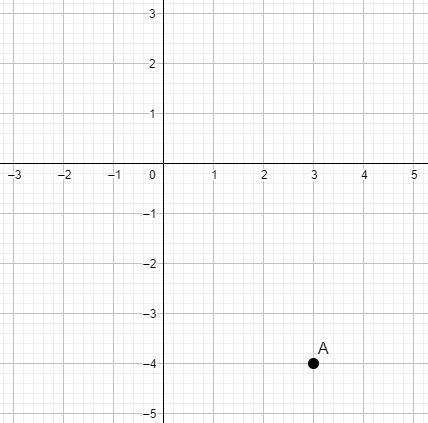
- \left(0,-1\right)
- \left(-1,-2\right)
- \left(\mathrm{0,0}\right)
Solución:
Para encontrar el camino correcto hasta el punto B , solo debemos seguir las instrucciones que nos da el enunciado en los primeros incisos. Comencemos por recorrer 6 cuadros en dirección al norte, es decir, hacia arriba.
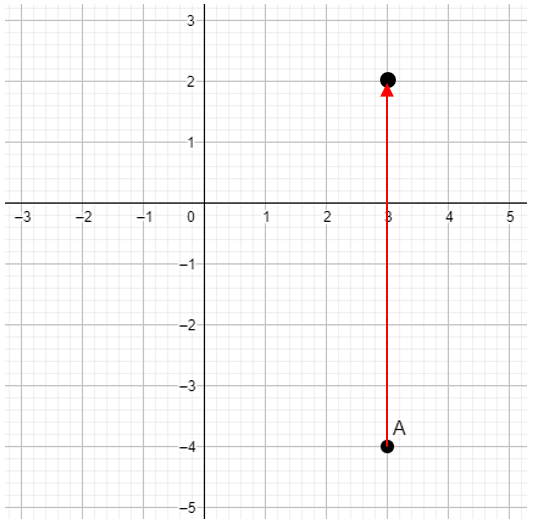
Ahora vamos 2 cuadros al oeste y 1 al sur.
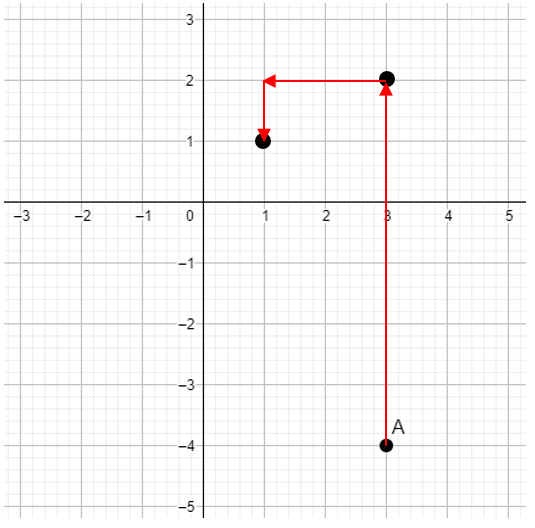
De nuevo 2 cuadros al oeste.
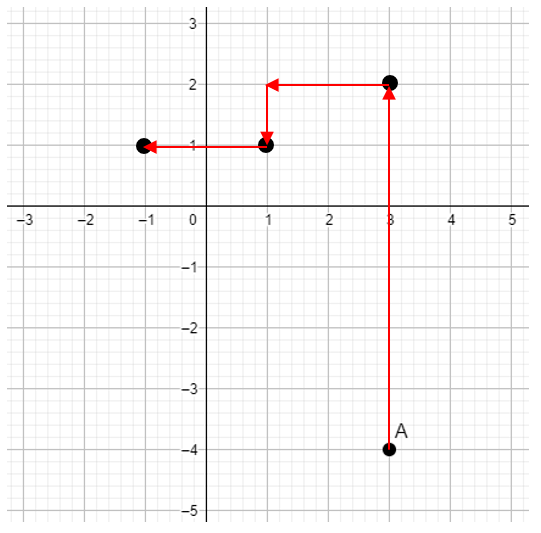
Llegamos al punto final B bajando tres posiciones.
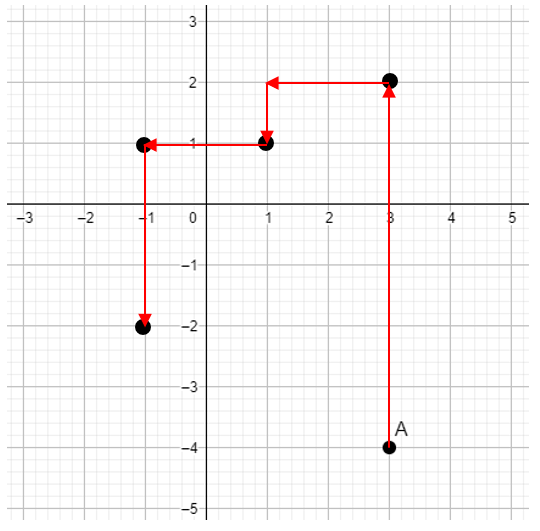
El punto final del recorrido es \left(-1,-2\right) .
Comparando con las opciones, la respuesta correcta es la b).


