¡Hola aspirante! En esta tutorial resolveremos la primera parte del examen simulacro de la Guía EXANI II para el módulo de Aritmética. Iniciamos desde el reactivo 1 hasta el 30.

Resuelve los problemas por tu cuenta antes de checar la solución. Es importante que desarrolles tu capacidad de análisis y solución de problemas antes del examen.
Estructura del EXANI II
La prueba de ingreso EXANI II, consta de dos partes: habilidades y conocimientos y los módulos específicos. Algunas universidades aplican una prueba diagnóstico de inglés, la cual no cuenta para aprobar el examen.
Examen de habilidades y conocimientos
La primera parte del examen se aplica para todas las carreras y tiene una extensión de 90 reactivos: 60 de Español y 30 de Matemáticas. La siguiente tabla resume la distribución de los reactivos en la prueba:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
Por otro lado, en la segunda parte los estudiantes deben responder 2 módulos específicos, que varían de acuerdo a la carrera. Debes revisar la convocatoria de tu universidad para conocer cuáles de los 15 módulos debes estudiar.
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Aritmética EXANI II
En la siguiente tabla te mostramos la distribución de los 24 reactivos de aritmética, con el temario desglosado que va para el examen.
| Subáreas | Temas | Num. de reactivos |
|---|---|---|
| Principios de números reales | Leyes de los signos | 14 |
| Leyes de los exponentes | ||
| Jerarquía de operaciones | ||
| Múltiplos y divisores | ||
| Problemas con números reales | Razones | 10 |
| Variaciones | ||
| Total | 24 |
Recomendaciones para resolver la guía interactiva
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
Para la operación aritmética que se muestra a continuación, ¿qué ley de signos debería aplicarse?
\left(-a\right)\left(b\right)
- La ley de los signos para la suma
- La ley de los signos para la división
- La ley de los signos para el producto
Solución:
Debido a que encerrar a los operandos entre paréntesis sin colocar ningún signo de suma, resta o división entre ellos, indica que se deben multiplicar; la ley de signos que debe aplicarse es la del producto.
Como a es negativo y b positivo, el resultado de multiplicarlos será negativo teniendo en cuenta dicha ley de signos. La respuesta correcta es el inciso c).
Reactivo 2
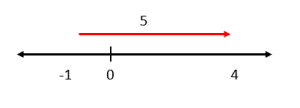
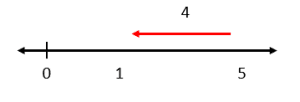
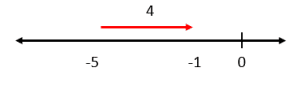
Dada la siguiente operación aritmética, seleccione la imagen que posiciona correctamente los operandos y el resultado sobre la recta real.
4-5=-1
Solución:
Sobre la recta real, la suma y la resta pueden expresarse como desplazamientos a la derecha o hacia la izquierda respectivamente. Para la resta del enunciado, tomamos al primer operando: 4, y nos desplazamos hacia la izquierda 5 posiciones.
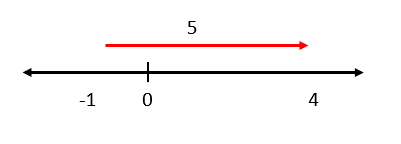
Examinando a los incisos, vemos que ninguno corresponde con la solución. Valiéndonos de la propiedad conmutativa de la suma, cambiamos de lugar al 4 y -5.
4-5=-1\to -5+4=-1
Esto significa pararnos en -5 y desplazarnos 4 posiciones hacia la derecha.
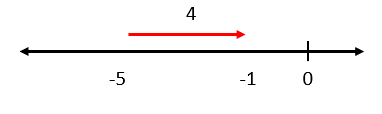
Comparando con los incisos, la respuesta correcta es c).
Reactivo 3
Resuelva la siguiente operación aritmética aplicando correctamente las leyes de los signos.
-3\left[4-\left(9-8\right)\right]+26\left[\frac{3}{2}-\left(4-3\right)\right]
- \frac{4}{5}
- 3
- 4
Solución:
Para resolver el problema, debemos recordar las reglas de jerarquía de operaciones y signos de agrupación. El orden de solución es:
- Llaves
- Corchetes
- Paréntesis
- Potencias y raíces
- Productos y cocientes
- Sumas y restas
La importancia disminuye a medida que bajamos en la lista. Teniendo esto en cuenta, debemos resolver primero el interior de los corchetes.
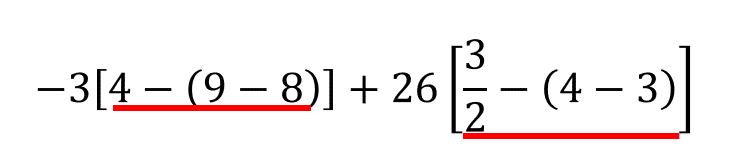
Ahora, dentro de los corchetes aplicando la jerarquía de operaciones, determinamos que hay que resolver el interior de los paréntesis.
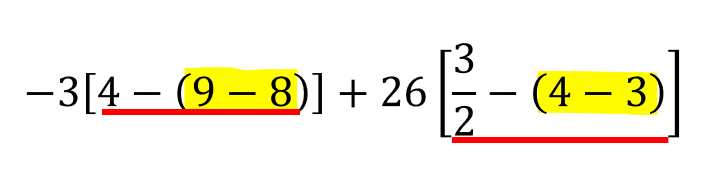
Resolviendo:
-3\left[4-\left(9-8\right)\right]+26\left[\frac{3}{2}-\left(4-3\right)\right]=-3\left[4-\left(1\right)\right]+26\left[\frac{3}{2}-\left(1\right)\right]
Eliminamos los paréntesis multiplicando el signo externo por el número.
-3\left[4-\left(1\right)\right]+26\left[\frac{3}{2}-\left(1\right)\right]=-3\left[4-1\right]+26\left[\frac{3}{2}-1\right]
Resolvemos lo que queda en el interior de los corchetes.
-3\left[4-1\right]+26\left[\frac{3}{2}-1\right]=-3\left[3\right]+26\left[\frac{1}{2}\right]
Deshacemos los corchetes resolviendo los productos indicados.
-3\left[3\right]+26\left[\frac{1}{2}\right]=-9+13
Finalmente, restamos.
-9+13=4
-3\left[4-\left(9-8\right)\right]+26\left[\frac{3}{2}-\left(4-3\right)\right]=4
La respuesta correcta es el inciso c).
Reactivo 4
Identifique la frase que ejemplifica la aplicación de la radicación a una cantidad.
- El promedio académico de un estudiante, es igual a la suma de sus calificaciones dividida por el número de evaluaciones
- El área de un cuadrado es igual a la segunda potencia de su lado
- La hipotenusa de un triángulo rectángulo es igual a la raíz cuadrada de la suma de sus catetos
Solución:
Analizando las frases de los incisos, tenemos que tanto a) como b) establecen sumas, divisiones y productos, pero no hay ninguna raíz cuadrada. Por otra parte, el inciso c) indica de manera explícita una raíz cuadrada.
La hipotenusa de un triángulo rectángulo es igual a la raíz cuadrada de la suma de sus catetos.
h=\sqrt{{c}_{1}^{2}+{c}_{2}^{2}}
La respuesta correcta es el inciso c).
Reactivo 5
Dadas las fracciones {f}_{1}=\frac{22}{7} y {f}_{2}=\frac{14}{11} calcule: la suma, la resta {f}_{1}-{f}_{2} y el producto.
- \frac{340}{77}, \frac{144}{77}, 4
- 4, \frac{344}{77}, \frac{144}{77}
- \frac{144}{77}, \frac{344}{77}, 4
Solución:
Iniciamos calculando la suma de las fracciones.
\frac{22}{7}+\frac{14}{11}
Aplicamos el procedimiento para fracciones con distinto denominador.
\frac{22}{7}+\frac{14}{11}=\frac{\left(22\right)\left(11\right)+\left(7\right)\left(14\right)}{\left(7\right)\left(11\right)}
Resolvemos los productos.
\frac{\left(22\right)\left(11\right)+\left(7\right)\left(14\right)}{\left(7\right)\left(11\right)}=\frac{242+98}{77}=\frac{340}{77}
Ahora, resolvemos la resta.
{f}_{1}-{f}_{2}=\frac{22}{7}-\frac{14}{11}
Operamos de la misma forma que con la suma, pero cambiando el signo “+” por un “-”.
\frac{22}{7}-\frac{14}{11}=\frac{\left(22\right)\left(11\right)-\left(7\right)\left(14\right)}{\left(7\right)\left(11\right)}=\frac{242-98}{77}=\frac{144}{77}
Finalmente, calculamos el producto. La fracción resultante se obtiene multiplicando los numeradores y denominadores respectivamente.
\frac{22}{7}\times \frac{14}{11}=\frac{\left(22\right)\left(14\right)}{\left(7\right)\left(11\right)}=\frac{308}{77}
Esta fracción puede reducirse.
\frac{308}{77}=4
Ordenando los tres resultados:
\frac{340}{77}, \frac{144}{77}, 4
La respuesta correcta es el inciso a).
Reactivo 6
Relacione correctamente las propiedades de los radicales en la columna izquierda con las igualdades en la columna derecha.

- 1c, 2b, 3a
- 1b, 2a, 3c
- 1a, 2b, 3c
Solución:
Para relacionar correctamente las propiedades de la izquierda con las operaciones de la derecha, es necesario conocer previamente dichas propiedades de los radicales.
Radical como exponente fraccionario.

1c.
Producto de radicales con igual índice.
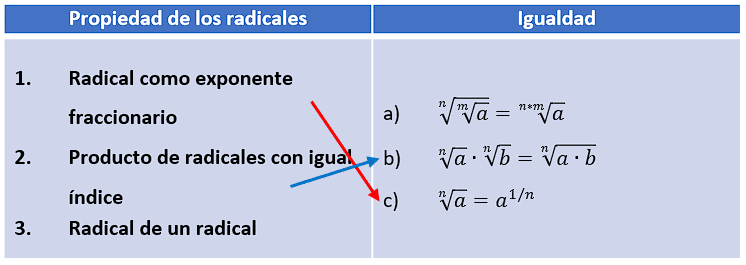
2b.
Por descartes: 3a. Uniendo todas las respuestas parciales: 1c, 2b, 3a.
La respuesta correcta es el inciso a).
Reactivo 7
Encuentre el resultado más simplificado de la siguiente expresión aritmética, aplicando las propiedades que sean necesarias.
\frac{{2}^{2}-{4}^{2}}{{3}^{2}-5}
- \frac{4}{5}
- -3
- \frac{1}{3}
Solución:
Siguiendo con las reglas de la jerarquía de operaciones, iniciamos resolviendo las potencias.
\frac{{2}^{2}-{4}^{2}}{{3}^{2}-5}=\frac{4-16}{9-5}
Resolvemos las operaciones en la fracción.
\frac{4-16}{9-5}=\frac{-12}{4}=-3
Indicamos como respuesta correcta al inciso b).
Reactivo 8
Transforma la fracción mixta 4\frac{1}{2} a fracción impropia.
- \frac{5}{2}
- \frac{9}{2}
- \frac{8}{2}
Solución:
La notación de las fracciones mixtas, permiten contraer la suma entre el número entero de la izquierda, con la fracción de la derecha.
4\frac{1}{2}=4+\frac{1}{2}
Es decir, la forma impropia se encuentra resolviendo esta suma.
4+\frac{1}{2}=\frac{\left(4\right)\left(2\right)+1}{2}=\frac{9}{2}
La respuesta correcta es el inciso b).
Reactivo 9
Calcule la siguiente expresión aritmética. Simplifique las fracciones mixtas para simplificar su resolución.
\frac{4\frac{1}{2}-4}{2\frac{1}{2}}
- 5
- \frac{1}{5}
- 1
Solución:
Convertimos en fracciones impropias a las expresadas en forma mixta.
\frac{4\frac{1}{2}-4}{2\frac{1}{2}}=\frac{4+\frac{1}{2}-4}{2+\frac{1}{2}}
Resolvemos la suma.
\frac{4+\frac{1}{2}-4}{2+\frac{1}{2}}=\frac{\frac{\left(4\right)\left(2\right)+1}{2}-4}{\frac{\left(2\right)\left(2\right)+1}{2}}=\frac{\frac{8+1}{2}-4}{\frac{4+1}{2}}=\frac{\frac{9}{2}-4}{\frac{5}{2}}
Ahora resolvemos la resta del numerador.
\frac{\frac{9}{2}-4}{\frac{5}{2}}=\frac{\frac{9-\left(2\right)\left(4\right)}{2}}{\frac{5}{2}}=\frac{\frac{9-8}{2}}{\frac{5}{2}}=\frac{\frac{1}{2}}{\frac{5}{2}}
Simplificamos el cociente de fracciones.
\frac{\frac{1}{2}}{\frac{5}{2}}=\frac{1}{2}÷\frac{5}{2}=\frac{\left(2\right)\left(1\right)}{\left(2\right)\left(5\right)}=\frac{1}{5}
Finalmente:
\frac{4\frac{1}{2}-4}{2\frac{1}{2}}=\frac{1}{5}
Indicamos como respuesta correcta al inciso b).
Reactivo 10
El encargado de una alberca escolar, ha notado que la misma se llena completamente en 2 horas. Si el volumen total de la alberca es de 1500 litros, ¿cuál es el valor de la razón en la que se llena la alberca en litros por minuto?
- 11 \mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}
- 12 \mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}
- 12.5 \mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}
Solución:
El problema nos pide expresar mediante una razón, la rapidez con la que dicha alberca gana volumen de agua respecto del tiempo. Iniciamos convirtiendo las 2 horas a minutos.
Sabemos que 1 hora tiene 60 minutos.
2 \mathrm{h}\cdot \frac{60 \mathrm{m}\mathrm{i}\mathrm{n}}{1 \mathrm{h}}=120 \mathrm{m}\mathrm{i}\mathrm{n}
Dividimos ahora los 1500 litros entre los 120 minutos.
\frac{1500 \mathrm{L}}{120 \mathrm{m}\mathrm{i}\mathrm{n}}=12.5 \mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}
La alberca se llena a razón de 12.5 litros por minuto.
Indicamos como respuesta correcta al inciso c).
Reactivo 11
Dada la siguiente desigualdad, resuelva las operaciones indicadas y diga si se cumple o no la desigualdad final.
{2}^{2}-\frac{3}{4}+\frac{1}{4}>\frac{3}{2}+{2}^{2}-3
- La desigualdad es cierta
- La desigualdad es falsa
- Se trata de una igualdad
Solución:
Las desigualdades nos permiten expresar relaciones entre cantidades numéricas más allá de que puedan ser iguales. Primero, es necesario resolver las operaciones indicadas en ambos miembros. Iniciamos calculando las potencias.
{2}^{2}-\frac{3}{4}+\frac{1}{4}>\frac{3}{2}+{2}^{2}-3\to 4-\frac{3}{4}+\frac{1}{4}>\frac{3}{2}+4-3
Ahora, vamos con las sumas y restas respectivamente.
4-\frac{3}{4}+\frac{1}{4}>\frac{3}{2}+4-3\to \frac{13}{4}+\frac{1}{4}>\frac{11}{2}-3
\frac{13}{4}+\frac{1}{4}>\frac{11}{2}-3\to \frac{7}{2}>\frac{5}{2}
Multiplicamos ambos miembros por 2. El sentido de la desigualdad se mantiene porque el factor es positivo.
2\cdot \frac{7}{2}>2\cdot \frac{5}{2}\to 7>5
La desigualdad es cierta, el número 7 es mayor que el número 5.
Indicamos como respuesta correcta al inciso a).
Reactivo 12
Joaquín es un estudiante universitario que está calculando cuánto dinero gasta al mes. Las últimas facturas indican que pagó 560$ en alquiler, 400$ en comida, 180$ para desplazarse a la universidad y 590$ en gastos varios. ¿Cuánto dinero necesita Joaquín mensualmente?
- Menos de 1700$
- Al menos 1730$
- Más de 200$
Solución:
La suma de todos los gastos de Joaquín en un mes es:
560+400+180+590=1730 \mathrm{\$}
Entonces, Joaquín necesita por lo menos 1730$ al mes.
La respuesta correcta es el inciso b).
Reactivo 13
Un auto de segunda mano, pero en excelentes condiciones cuesta 100,000$, mientras que uno totalmente nuevo 20,000$ más que el de segunda mano. Si un coche del mismo modelo, pero del año cuesta la semisuma de los coches anteriores, ¿cuánto se debería pagar por este último?
- 110,000$
- 220,000$
- 120,000$
Solución:
Iniciemos estableciendo el costo de los dos primeros coches.
{\mathrm{C}}_{\mathrm{s}\mathrm{m}}=100000\$
{\mathrm{C}}_{\mathrm{n}}={\mathrm{C}}_{\mathrm{s}\mathrm{m}}+20000\$=100000\$+20000\$=120000\$
Ahora, el costo del tercer coche se obtiene mediante la semisuma de los costos anteriores. La semisuma de dos cantidades, es igual a la suma de las cantidades divididas entre 2.
{\mathrm{C}}_{\mathrm{a}\mathrm{ñ}\mathrm{o}}=\frac{{\mathrm{C}}_{\mathrm{s}\mathrm{m}}+{\mathrm{C}}_{\mathrm{n}}}{2}=\frac{100000+120000}{2}=\frac{220000}{2}=110000\$
El coche del año actual tiene un costo de 110,000$ pesos.
La respuesta correcta es el inciso a).
Reactivo 14
Un usuario abona a su cuenta bancaria 50,000$ como concepto de ahorros. Pasada una semana retira 25,000$ y dos días después paga una cuenta de 9,000$. Al final del mes abona 20,000$ más. ¿Cuál es el balance de la cuenta bancaria?
- 34,000$
- 25,000$
- 36,000$
Solución:
Para encontrar el saldo final, debemos ir sumando y restando los ingresos y egresos respectivamente. Al inicio del mes, el usuario tiene un balance de 50,000$.
{\mathrm{S}}_{1}=\mathrm{50,000}
Luego hace un retiro de 25,000$ pesos.
{\mathrm{S}}_{2}=\mathrm{50,000}-\mathrm{25,000}=\mathrm{25,000}
Dos días después hace un pago, esto cuenta como egreso.
{\mathrm{S}}_{3}=\mathrm{25,000}-\mathrm{9,000}=\mathrm{16,000}\$
Finalmente, el usuario ingresa 20,000$.
{\mathrm{S}}_{4}=\mathrm{16,000}+\mathrm{20,000}=\mathrm{36,000}\$
El saldo final es de 36,000 pesos.
Indicamos como respuesta correcta al inciso c).
Reactivo 15
José ha iniciado un nuevo emprendimiento y, como buen comerciante, estaba revisando las finanzas de la última semana. Se dio cuenta que el lunes ganó 2,500$ y que existe una proporción de 4/3 entre dos días consecutivos: día actual entre día anterior. ¿Cuánto dinero ganaría José de su negocio si trabaja 6 días a la semana?
- 30,640$
- 35,640$
- 34,640$
Solución:
El enunciado indica que José ganó 2,500 pesos y que existen una razón entre lo ganado el día actual y el día siguiente de 4/3, es decir:
\frac{{\mathrm{D}}_{\mathrm{a}\mathrm{c}}}{{\mathrm{D}}_{\mathrm{a}\mathrm{n}}}=\frac{4}{3}\to {\mathrm{D}}_{\mathrm{a}\mathrm{c}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{a}\mathrm{n}}
Esto quiere decir que, estando en el martes la ganancia será 4/3 multiplicado por la ganancia del lunes. La del miércoles 4/3 por la ganancia del martes y así sucesivamente hasta llegar al sábado, sexto día de la semana que labora José.
Ganancia del lunes.
{\mathrm{D}}_{\mathrm{L}}=2500
Ganancia del martes.
{\mathrm{D}}_{\mathrm{M}\mathrm{a}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{L}}=3333.3
Ganancia del miércoles.
{\mathrm{D}}_{\mathrm{M}\mathrm{i}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{M}\mathrm{a}}=4444.4
Ganancia del jueves.
{\mathrm{D}}_{\mathrm{J}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{M}\mathrm{i}}=5926
Ganancia del viernes.
{\mathrm{D}}_{\mathrm{V}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{J}}=7901.2
Ganancia del sábado.
{\mathrm{D}}_{\mathrm{S}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{V}}=10535
La ganancia de toda la semana es la suma del ingreso por los 6 días hábiles.
\mathrm{G}=2500+3333.3+4444.4+5926+7901.2+10535=34639.9
Finalmente:
\mathrm{G}=\mathrm{34,640}\mathrm{\$}
La respuesta correcta es el inciso c).
Reactivo 16
Dada la siguiente cuadrícula con algunos rectángulos colocados de manera irregular, indique cuál de las opciones permite obtener el total de los rectángulos sin contar uno a uno.
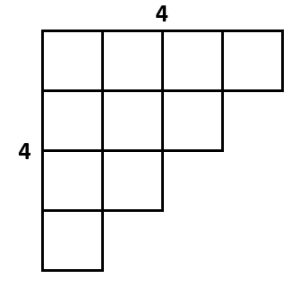
- 4\times 4
- 4\times 4-2\times 2-2
- 4\times 4-2-1
Solución:
Debemos encontrar una expresión aritmética que nos permita calcular el total de casillas que conforman a la cuadrícula. Iniciamos indicando que, si estuviese completa, el total sería 4\times 4 .
Dibujando sobre la figura, estas son las casillas faltantes.
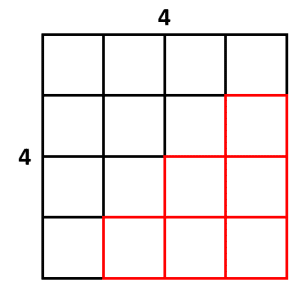
Vemos que se forma una cuadrícula de 2\times 2 junto a otros dos rectángulos uno en la parte superior y otro a la izquierda en la zona inferior. Debemos restar 2\times 2+2 a la cuadrícula completa para obtener el total de cuadros negros.
\mathrm{C}\mathrm{u}\mathrm{a}\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{ }\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{s}=4\times 4-2\times 2-2
La respuesta correcta es el inciso b).
Reactivo 17
Esteban va a una papelería para comprar algunas libretas y lápices, los cuales tienen un precio de 15$ y 5$ respectivamente. Al llegar a la caja, se da cuenta que el total fue de 120$, si Esteban compró la misma cantidad de libretas que de lápices, ¿cuánto llevó de cada una?
- Llevó 6 de cada una
- Llevó 5 de cada una
- Llevó 7 de cada una
Solución:
Lo primero que podemos extraer del enunciado, es el precio unitario de las libretas y los lápices.
{\mathrm{P}}_{\mathrm{L}\mathrm{a}}=5\$
{\mathrm{P}}_{\mathrm{L}\mathrm{i}}=15\$
Llamaremos al total de lápices como \mathrm{L}\mathrm{a} y al total de libretas \mathrm{L}\mathrm{i} . El costo total a pagar es igual al total de lapiceros por su precio más, el total de libretas por su precio.
120=5\mathrm{L}\mathrm{a}+15\mathrm{L}\mathrm{i}
Por otra parte, Esteban llevó la misma cantidad de lápices que de libretas.
\mathrm{L}\mathrm{a}=\mathrm{L}\mathrm{i}
Dejamos a la expresión anterior con solo \mathrm{L}\mathrm{a} .
120=5\mathrm{L}\mathrm{a}+15\mathrm{L}\mathrm{i}\to 120=5\mathrm{L}\mathrm{a}+15\mathrm{L}\mathrm{a}\to 120=20\mathrm{L}\mathrm{a}
Despejamos:
\mathrm{L}\mathrm{a}=\frac{120}{20}=6\mathrm{ }\mathrm{l}\mathrm{a}\mathrm{p}\mathrm{i}\mathrm{c}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{s}
Debido a que \mathrm{L}\mathrm{a}=\mathrm{L}\mathrm{i} :
\mathrm{L}\mathrm{i}=6\mathrm{ }\mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}
Estaban llevando 6 libretas y 6 lapiceros de la tienda.
La respuesta correcta es el inciso a).
Reactivo 18
Se sabe que un ordenador gaming cuesta el doble que un ordenador de oficina básico. ¿Cuál de las siguientes comparaciones es correcta?
- El precio del ordenador gaming es igual a la mitad del precio del ordenador de oficina
- El precio del ordenador de oficina es mayor que la mitad del precio del ordenador gaming
- La cuarta parte del precio del ordenador gaming es menor el precio del ordenador de oficina
Solución:
Para resolver el problema, expresamos a la relación de precios entre los computadores como una razón.
\frac{{\mathrm{P}}_{\mathrm{g}}}{{\mathrm{P}}_{\mathrm{o}}}=2
De esta razón obtenemos dos igualdades equivalentes:
\frac{{\mathrm{P}}_{\mathrm{g}}}{{\mathrm{P}}_{\mathrm{o}}}=2\to {\mathrm{P}}_{\mathrm{g}}=2{\mathrm{P}}_{\mathrm{o}}
El precio del ordenador gaming es el doble que el de oficina.
\frac{{\mathrm{P}}_{\mathrm{g}}}{{\mathrm{P}}_{\mathrm{o}}}=2\to {\mathrm{P}}_{\mathrm{o}}=\frac{1}{2}{\mathrm{P}}_{\mathrm{g}}
El precio del ordenador de oficina es la mitad que el gaming.
Las dos primeras aseveraciones son falsas. Porque el precio del ordenador de oficina no es mayor (en ninguna proporción) al ordenador gaming. Por descartes, la respuesta correcta es el inciso c).
Reactivo 19
La suma de dos cantidades enteras es 1300 y su resta es igual a 300. ¿Cuál es el valor de dichas cantidades?
- 1000 y 200
- 300 y 1000
- 500 y 800
Solución:
Debemos expresar las relaciones en lenguaje matemático. Llamaremos a las cantidades x y y .
La suma de dos cantidades enteras es 1300…
x+y=1300
…su resta es igual a 300.
x-y=300
Despejamos a x .
x=y+300
Sustituimos en la primera expresión.
y+300+y=1300\to 2y=1000
\therefore y=500
Finalmente:
x=500+300=800
Las cantidades enteras son 500 y 800.
La respuesta correcta es el inciso c).
Reactivo 20
Un automóvil tiene una autonomía del combustible de 2 kilómetros por litro. Si el conductor necesita realizar un viaje de 150 kilómetros ¿Cuántos litros de combustible extra debe llevar con él si el tanque tiene capacidad máxima de 40 litros?
- 20 litros extra
- 30 litros extra
- 35 litros extra
Solución:
La autonomía de combustible del automóvil la podemos expresar como la razón:
\mathrm{A}=\frac{2\mathrm{ }\mathrm{k}\mathrm{m}}{1 \mathrm{L}}=2\frac{\mathrm{k}\mathrm{m}}{\mathrm{L}}
Ahora, dividimos los 150 kilómetros del viaje para obtener el total de combustible.
\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{b}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{b}\mathrm{l}\mathrm{e}=\frac{150}{2}=75 \mathrm{L}\mathrm{i}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
Si el tanque tiene 40 litros, el conductor deberá llevar consigo al menos otros 35 litros de combustible para cubrir el viaje. La respuesta correcta es el inciso c).
Reactivo 21
En una carrera de fórmula 1, un corredor A se dirige por la recta final a una razón de 120 kilómetros por hora y el corredor en segundo lugar B, tiene una distancia con el primero de 20 metros y se desplaza a razón de 130 kilómetros por hora.
Si desde el momento en que se toman estos datos el corredor A está a 50 metros de la meta, ¿quién ganará la competición?
- Gana el corredor A
- Gana el corredor B
- Llegan empatados
Solución:
Hagamos una representación gráfica de la posición que tienen los corredores en ese instante.
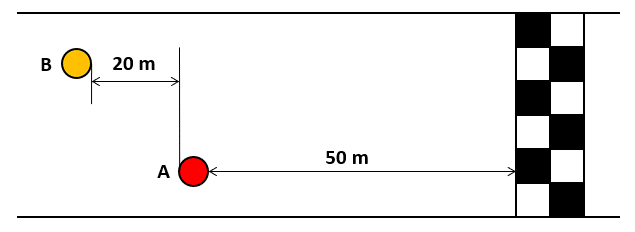
Con esto, sabemos que el corredor A está a 50 metros de la meta, mientras que el B se encuentra a 70 metros. Podemos calcular el tiempo que tardará cada uno en llegar a la meta, teniendo en cuenta la velocidad de cada uno.
Tiempo del corredor A.
120\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\to {t}_{A}=\frac{50}{120}=0.4166 \mathrm{h}
Tiempo del corredor B.
130\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\to {t}_{B}=\frac{70}{130}=0.5384 \mathrm{h}
Aunque el corredor B se desplaza a una mayor velocidad, el corredor A tardará menos tiempo. La respuesta correcta es el inciso a).
Reactivo 22
Eliezer le propone a su hermano menor ahorrar juntos para comprar un nuevo videojuego. Han acordado aportar de forma proporcional a sus edades. Si Eliezer tiene 12 años y su hermano menor tiene 8 años, ¿cuánto dinero deberá aportar Eliezer si el videojuego cuesta 3,800$?
- 1520$
- 2280$
- 3000$
Solución:
En este caso, la suma de las edades de los hermanos equivale al costo total del videojuego.
20\to 3800
Si Eliezer tiene 12 años, entonces podemos aplicar una regla de tres simple para calcular su aporte.
20\to 3800
12\to x
Nos queda:
x=\frac{12\cdot 3800}{20}=2280\$
Eliezer debe aportar 2280 pesos para la compra del juego con su hermano.
La respuesta correcta es el inciso b).
Reactivo 23
Un comerciante compró cierto cargamento de maíz en 80,000$ pesos y lo vendió para obtener una ganancia de 25,000$. Si el comerciante vendió el maíz a 100$ el kilo, ¿cuántos kilogramos de maíz conformaban el cargamento?
- 1050 kilogramos de maíz
- 1000 kilogramos de maíz
- 1200 kilogramos de maíz
Solución:
Para cualquier producto tenemos un precio de compra PC , un precio de venta PV y una cantidad de unidades n . La ganancia se obtiene como la diferencia:
\mathrm{G}=\mathrm{n}\mathrm{P}\mathrm{V}-\mathrm{n}\mathrm{P}\mathrm{C}
El enunciado nos indica el total que pagó el usuario por la mercancía. Lo llamaremos: precio total de inversión \mathrm{P}\mathrm{T}\mathrm{I} .
\mathrm{G}=\mathrm{n}\mathrm{P}\mathrm{V}-\mathrm{P}\mathrm{T}\mathrm{I}
Tenemos la ganancia, el precio de venta por kilogramo y la inversión total. Despejamos el total de kilogramos adquiridos.
\mathrm{G}=\mathrm{n}\mathrm{P}\mathrm{V}-\mathrm{P}\mathrm{T}\mathrm{I}\to \mathrm{n}=\frac{\mathrm{G}+\mathrm{P}\mathrm{T}\mathrm{I}}{\mathrm{P}\mathrm{V}}
Sustituimos.
\mathrm{n}=\frac{25000+80000}{100}=1050 \mathrm{k}\mathrm{i}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{o}\mathrm{s}
El comerciante compró un total de 1050 kilogramos de maíz.
La respuesta correcta es el inciso a).
Reactivo 24
Luis y su hermano se asocian para trabajar juntos como albañiles. Ha surgido un nuevo trabajo y la paga es de 12,000$ y la duración es de 10 días. ¿Cuánto dinero gana Luis al día si su hermano gana 500$?
- 500$
- 1200$
- 700$
Solución:
Teniendo la paga total del trabajo y los días de duración del proyecto, calculamos la paga diaria.
\mathrm{P}\mathrm{D}=\frac{12000}{10}=1200\frac{\mathrm{\$}}{\mathrm{d}\mathrm{í}\mathrm{a}}
Si el hermano de Luis gana 500$ diarios, entonces él se queda con lo que resta de los 1200 al día.
\mathrm{L}\mathrm{u}\mathrm{i}\mathrm{s}=1200-500=700\mathrm{\$}
Luis gana 700 pesos al día.
La respuesta correcta es el inciso c).
Reactivo 25
Un número es divisible por nueve si…
- Si es divisible entre 3
- Si la suma de sus dígitos es 9
- Si la suma de sus dígitos es múltiplo de 9
Solución:
El número 9 sólo es divisible por el 3, por sí mismo y por el 1. Teniendo en cuenta los incisos, la respuesta correcta es c).
Reactivo 26
Escriba en lenguaje matemático la siguiente frase en lenguaje natural.
La semiresta de 6 con 3 elevada a la segunda potencia.
- {\left[\frac{6-3}{2}\right]}^{2}
- {\left[\frac{3-6}{2}\right]}^{2}
- \frac{{\left(6-3\right)}^{2}}{2}
Solución:
Vamos a ir analizando la frase por partes hasta convertirla en expresión matemática.
La semiresta de 6 con 3…
La semirresta entre dos números, establece que debemos restarlos y dividirlos entre 2.
\frac{6-3}{2}
… elevada a la segunda potencia.
Debemos elevar al cuadrado a la semiresta de 6 con 3.
{\left(\frac{6-3}{2}\right)}^{2}
Comparando con los incisos, la respuesta correcta es el a).
Reactivo 27
Un instrumento de medición marca en determinado momento 100 psi y, luego de algunos minutos su lectura ha incrementado a 107 psi. ¿En cuánto porcentaje incrementó la medición?
- 10%
- 5%
- 7%
Solución:
Para calcular cualquier diferencia porcentual, empleamos la siguiente fórmula.
{\mathrm{\Delta }}_{\mathrm{\%}}=\frac{\mathrm{N}\mathrm{u}\mathrm{e}\mathrm{v}\mathrm{o}\mathrm{ }\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{r}-\mathrm{A}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{o}\mathrm{ }\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{r}}{\mathrm{A}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{o}\mathrm{ }\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{r}}\cdot 100\%
El nuevo valor es 107 psi y el antiguo valor es igual a 100 psi. Sustituimos.
{\mathrm{\Delta }}_{\mathrm{\%}}=\frac{107-100}{100}\cdot 100\%=\frac{7}{100}\cdot 100\%=7\%
La medición del instrumento se incrementa en un 7%.
La respuesta correcta es el inciso c).
Reactivo 28
A partir del número mostrado a continuación, ¿cuál de las siguientes frases es correcta?
\sqrt[3]{{2}^{4}}
- El resultado es indefinido en los reales
- Dos elevado a cuatro tercios
- Dos elevado a tres cuartos
Solución:
Vamos a ir analizando cada una de las frases en el enunciado, aquella que sea correcta será la respuesta al problema.
El resultado es indefinido en los reales.
Para que el resultado del radical no se encuentre definido en los reales, éste debería arrojar un número imaginario, pero ni el índice de la raíz es par ni el radicando es negativo.
Dos elevado a cuatro tercios.
Si expresamos a la operación como una potencia obtenemos:
\sqrt[3]{{2}^{4}}={\left({2}^{4}\right)}^{\frac{1}{3}}={2}^{\frac{4}{3}}
El inciso b) es la respuesta correcta al problema.
Reactivo 29
La gráfica que se muestra a continuación representa la relación entre voltaje y corriente de una resistencia de carbón convencional.
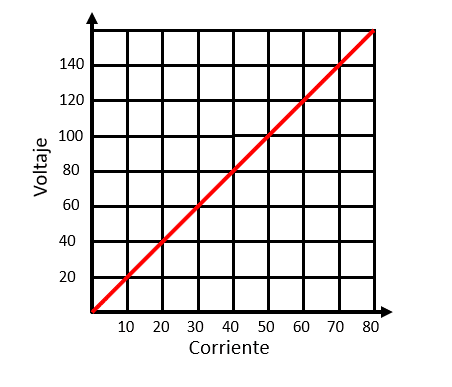
¿Cuál es la razón de crecimiento del voltaje cuando incrementa la corriente?
- 2 voltios por amperio
- 4 amperios por voltio
- 2 amperios por voltio
Solución:
Debido a que la relación entre la corriente y el voltaje es lineal, podemos calcular la razón de incremento como el cociente entre el mínimo cambio del voltaje sobre el mínimo cambio de la corriente.
\frac{20-0}{10-0}=\frac{20}{10}=2\frac{\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{s}}{\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}}
La razón de cambio es de 2 voltios por amperio.
Indicamos como respuesta correcta al inciso a).
Reactivo 30
La construcción de dos edificaciones en paralelo ha requerido el diseño de un sistema de acueductos para conectar a dichas infraestructuras al sistema de ductos de la ciudad. Desde el nodo más cercano la edificación A se encuentra a 180 metros y la edificación B a 250 metros del mismo nodo.
No deben existir cortes, ya que eso haría frágil el sistema de ductos y por temas económicos, el tubo empleado para la conexión de A se deberá emplear para la conexión de B. ¿Cuál es el máximo tamaño de tubería que debería utilizarse?
- 18 metros
- 10 metros
- 8 metros
Solución:
Aunque el enunciado sea largo, el problema nos solicita que calculemos una longitud de tubería que pueda emplearse tanto para A como para B.
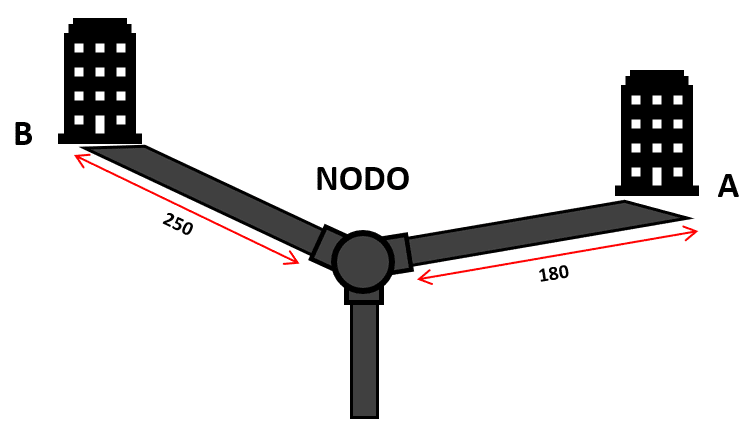
La máxima longitud de tubería para cubrir ambas distancias la encontramos con el máximo común divisor.
\mathrm{M}\mathrm{C}\mathrm{D}\left(180, 250\right)=10
La máxima distancia de tuberías que se puede emplear para los acueductos es de 10 metros. Indicamos como respuesta correcta al inciso b).