¿Necesitas ayuda con los reactivos de geometría del IPN? ¿Sí?, entonces llegaste al lugar correcto. En este tutorial vamos a resolver los primeros 10 reactivos de geometría y trigonometría de la guía de ingreso al IPN 2023.

El siguiente es un resumen de la convocatoria IPN 2023.
- Carreras ofertadas en IPN: 70+.
- Porcentaje de Aceptación: 20%.
- Preguntas en el examen de Admisión: 140 preguntas.
- Nuevos temas: historia e inglés (reading comprehension).
- Tipo: selección múltiple.
¿Sabes cuáles son las nuevas materias del examen? ¡El IPN ha sufrido grandes cambios para este 2023!
Estructura del Examen IPN
En la estructura del examen al IPN 2023, la cantidad de reactivos por asignatura cambia según el área de conocimientos de tu carrera. Las carreras en el Politécnico Nacional se dividen en 3 áreas:
- Ingeniería y Ciencias Físico Matemáticas IyCFM
- Ciencias Sociales y Administrativas CSA
- Ciencias Médico Biológias CMB
La siguiente tabla muestra la estructura de reactivos por materia para cada área.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
¿Qué tan difícil es el examen al IPN?
Todo aspirante al Instituto Politécnico Nacional se ha hecho la pregunta: ¿es difícil la prueba para entrar al IPN? Aunque no lo creas, la respuesta depende de un único factor: tu preparación antes del examen.
Para la convocatoria de este año se han agregado 2 asignaturas nuevas y la estructura ha cambiado. En la guía de geometría y trigonometría los reactivos tienen una complejidad aumentada respecto a los años anteriores.
Esto puede parecer desafiante, pero no te preocupes, si estudiar con anticipación no tendrás mayor problema para entender todos los temas del examen.
Temario geometría y trigonometría IPN 2023
Estos son los temas de geometría y trigonometría que deberás dominar antes de presentar el examen de ingreso:
- Funciones exponenciales y logarítmicas
- Concepto
- Propiedades
- Geometría euclidiana
- Elementos básicos
- Triángulos
- Polígonos
- Circunferencia
- Funciones trigonométricas
- Representación gráfica
- Identidades trigonométricas
- Razones trigonométricas
¿Cómo resolver la guía del IPN 2023?
Lo primero que te recomiendo, es examinar la bibliografía indicada por la guía del IPN 2023. Estudia el temario y comprende los fundamentos. Un error común entre los aspirantes consiste en estudiar los temas mientras resuelven la guía.
Estudiando de esta forma pierdes tiempo y vas a ciegas sin una metodología óptima a la hora de estudiar.
Los siguientes hacks te ayudarán a mejorar el desempeño, resolviendo la mayor cantidad de reactivos en el menor tiempo y así obtener los aciertos necesarios para quedar en tu carrera.
- Resuelve cada parte por tu cuenta antes de checar las respuestas. Utiliza este material a modo de consulta.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
- Te advierto que la guía del IPN 2023 tiene algunos errores, aquí te señalamos cuáles son.
Reactivo 1
Identificar cuál de los siguientes no se puede utilizar como criterio de congruencia de triángulos.
- LLL
- LAL
- ALA
- AAL
Solución:
Para resolver el problema, debemos recordar cuáles son los criterios de congruencia entre triángulos y el significado de la notación en los incisos. Cuando decimos que dos triángulos son congruentes, es porque tanto sus lados como ángulos tienen la misma medida, sin importar la posición relativa entre las figuras.
Ahora, dos triángulos se consideran congruentes de tres formas:
Si sus tres lados son iguales: LLL.
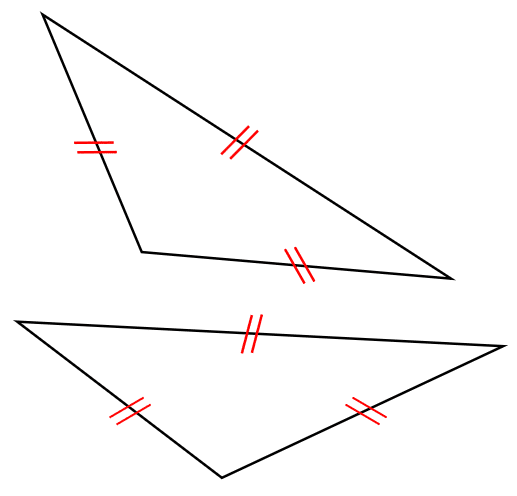
Si dos lados y el ángulo comprendido entre ellos, son iguales: LAL.
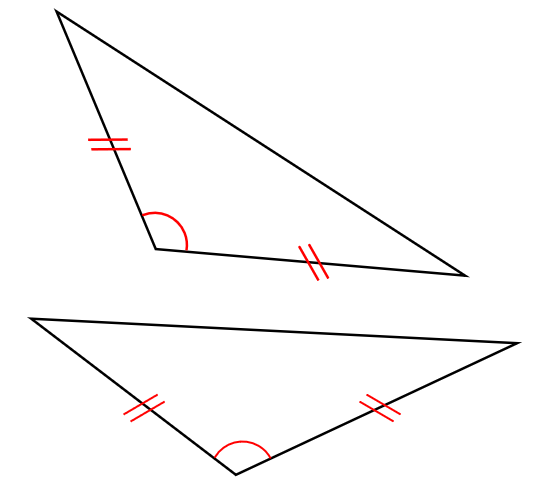
Si un lado y los ángulos adyacentes a dicho lado son iguales: ALA.
Teniendo en cuenta lo anterior, el único inciso que no muestra un criterio de congruencia entre triángulos es el d).
Reactivo 2
La función trigonométrica \mathrm{s}\mathrm{e}\mathrm{n}\left(\theta \right) es impar porque cumple con la siguiente condición:
- f\left(x\right)=f\left(-x\right)
- f\left(x\right)=-f\left(-x\right)
- f(-x)=-f\left(x\right)
- f(a\cdot x)={a}^{n}f\left(x\right)
Solución:
Las funciones impares son aquellas simétricas por rotación respecto al origen.
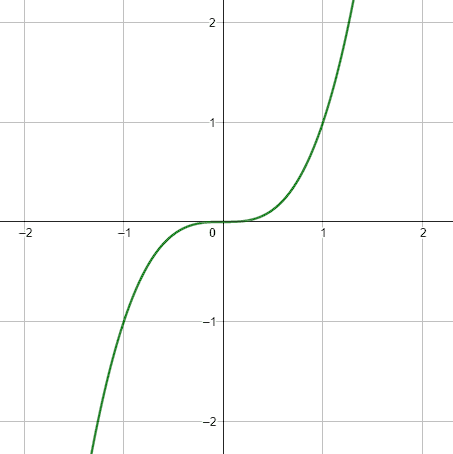
Para comprobar matemáticamente que una función f\left(x\right) es impar, se emplea la siguiente expresión:
f\left(-x\right)=-f\left(x\right)
Toda función que satisface esta igualdad es impar y viceversa. De esta forma, al ser el seno una función impar, la expresión que satisface es la del inciso c).
Reactivo 3
Si \widehat{A}\text{ y }\widehat{B} son ángulos conjugados y \widehat{A}={65}^{\circ } , encontrar el valor de \widehat{B} .
- 25°
- 115°
- 205°
- 295°
Solución:
Dos ángulos son conjugados, si la suma de estos es igual a 360°.
\widehat{A}+\widehat{B}=360°
Despejamos el ángulo \widehat{B} .
\widehat{B}=360°-\widehat{A}=360°-65°=295°
La respuesta correcta es el inciso d).
Reactivo 4
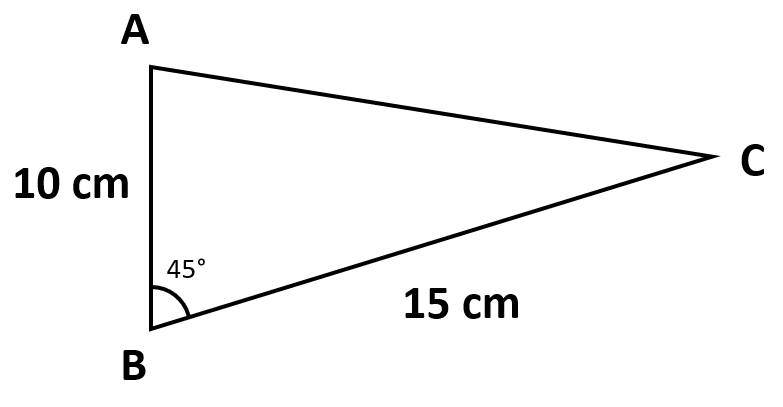
De acuerdo con la figura, determinar el lado \stackrel{-}{AC} del triángulo ∆ABC .
- 2\sqrt{13-6\sqrt{2}}
- 3\sqrt{13-6\sqrt{2}}
- 4\sqrt{13-6\sqrt{2}}
- 5\sqrt{13-6\sqrt{2}}
Solución:
Este reactivo puede resolverse de dos formas: descomponiendo el triángulo en dos triángulos rectángulos o aplicando la ley del coseno, porque tenemos 2 lados y un ángulo. Debido a que acelera la solución, vamos a emplear la ley del coseno.
A{C}^{2}=A{B}^{2}+B{C}^{2}-2\stackrel{-}{AB}\stackrel{-}{CB}\mathrm{cos}45°
El coseno de 45° es \frac{\sqrt{2}}{2} . Sustituimos todos los valores en la ecuación.
A{C}^{2}={\left(10\right)}^{2}+{\left(15\right)}^{2}-2\left(10\right)\left(15\right)\left(\frac{\sqrt{2}}{2}\right)
Simplificamos.
A{C}^{2}=100+225-300\left(\frac{\sqrt{2}}{2}\right)=325-150\sqrt{2}
Tanto el 325 como el 150 son divisibles por 25.
A{C}^{2}=25\left(13-6\sqrt{2}\right)
AC=5\sqrt{13-6\sqrt{2}}
Finalmente:
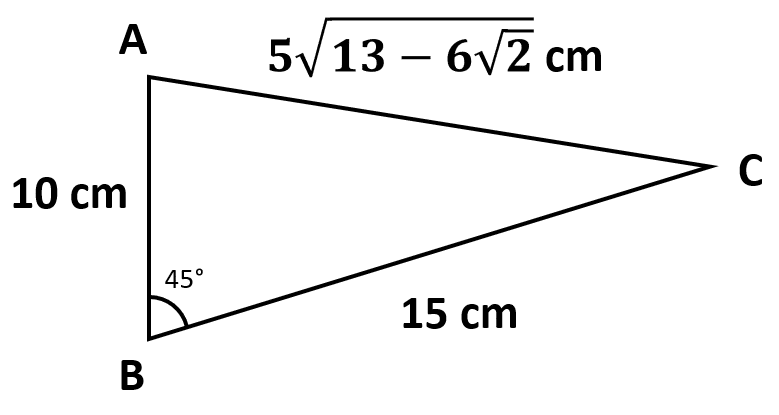
La respuesta correcta es el inciso d).
Reactivo 5
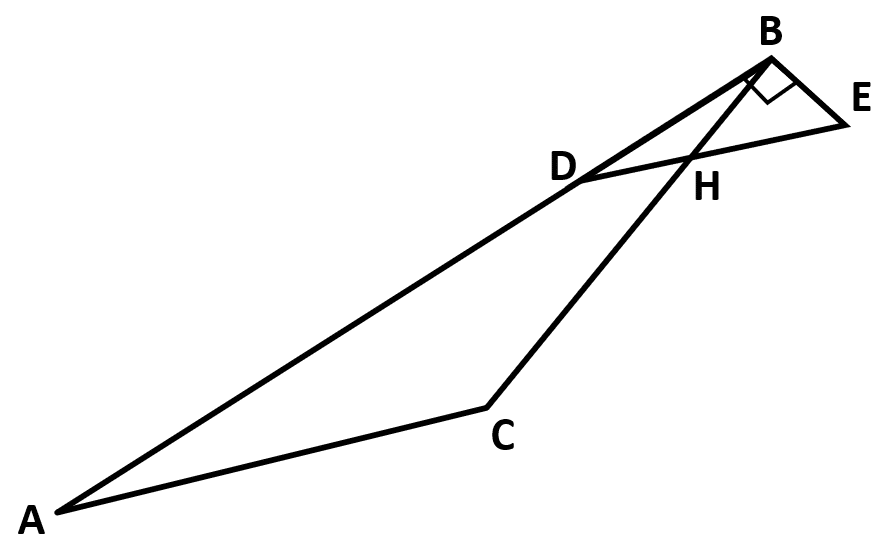
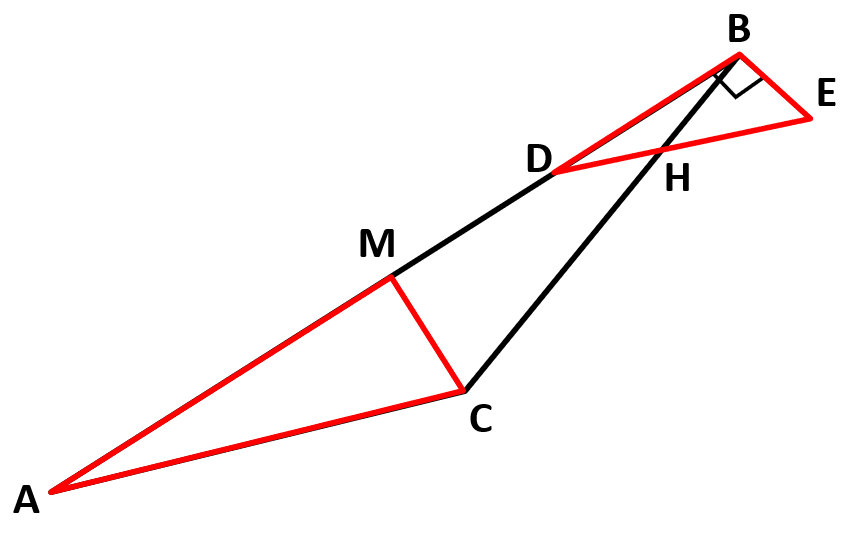
Identificar la longitud \stackrel{-}{HE} de la siguiente figura. Considerar que ∆ACB con altura 9.94 desde C es semejante al triángulo ∆DHB , AB=49 , AC=23 , BC=30 y BH=6 , BD=9.8 .
- 4.2
- 6.9
- 7.5
- 8.7
Solución:
Para resolver el problema, debemos calcular la longitud del segmento DH y DE , para obtener mediante una resta al segmento HE . Debido a que los triángulos ACB y DHB son proporcionales, podemos calcular la longitud del segmento DH aplicando el primer teorema de tales para triángulos semejantes.
Aplicando la semejanza entre los triángulos nos queda:
\frac{DH}{DB}=\frac{AC}{AB}\to DH=DB\cdot \frac{AC}{AB}
Sustituimos:
DH=\left(9.8\right)\left(\frac{23}{49}\right)=4.6
Ahora, aplicamos triángulos semejantes entre ACM y DEB . Donde M es el punto de la altura del triángulo ACB .
La semejanza la aplicamos respecto a los segmentos DB y DE .
\frac{DE}{DB}=\frac{AC}{AM}\to DE=DB\frac{AC}{AM}
La distancia AM se calcula aplicando el teorema de Pitágoras.
A{C}^{2}=A{M}^{2}+M{C}^{2}\to AM=\sqrt{A{C}^{2}-M{C}^{2}}
Sustituimos, recordando que MC es la altura del triángulo ACB respecto al punto C .
AM=\sqrt{{23}^{2}-{9.94}^{2}}=20.7
Sustituimos todo para calcular DE .
DE=\left(9.8\right)\frac{23}{20.7}=10.9
Finalmente:
HE=DE-DH=10.9-4.6=6.3
HE=6.3 \mathrm{c}\mathrm{m}
En los incisos hay un error con los decimales, pero, en teoría, la respuesta correcta es la opción b).
Reactivo 6
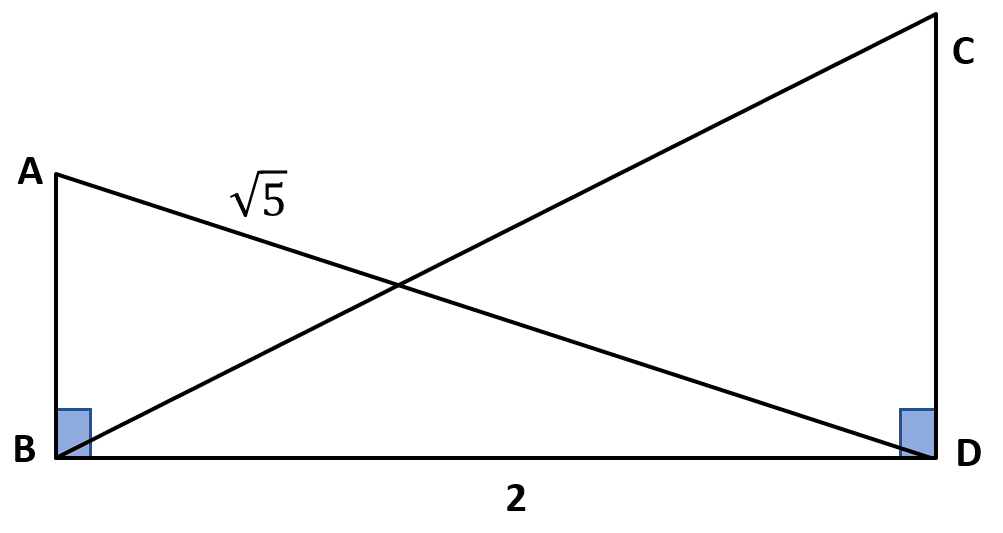
Calcular la longitud del segmento CB que se muestra en la siguiente figura, si cumple que CD=3AB y AD=\sqrt{5} .
- \sqrt{10}
- \sqrt{11}
- \sqrt{12}
- \sqrt{13}
Solución:
Para resolver el problema, debemos aplicar el teorema de Pitágoras en conjunto a las relaciones dadas por el enunciado. Nuestra incógnita es la hipotenusa del triángulo BDC , la cual se calcula como:
CB=\sqrt{{2}^{2}+C{D}^{2}}=\sqrt{4+C{D}^{2}}
Por otra parte, tenemos que:
CD=3AB
El lado AB lo podemos calcular aplicando el teorema de Pitágoras sobre el triángulo ABD .
A{D}^{2}=B{D}^{2}+A{B}^{2}\to AB=\sqrt{A{D}^{2}-B{D}^{2}}
Sustituimos.
AB=\sqrt{5-4}=1
\therefore CD=3\left(1\right)=3
Finalmente:
CB=\sqrt{4+{3}^{2}}=\sqrt{4+9}=\sqrt{13}
La respuesta correcta es el inciso d).
Reactivo 7
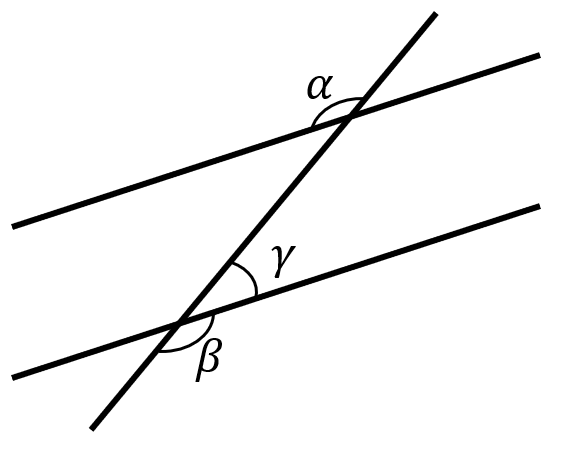
Calcular los ángulos \alpha ,\beta ,\gamma de la figura con base en la siguiente información:
- \alpha mide 6x-14
- \beta mide la mitad del ángulo 4x+\frac{4}{3}
- 25, 25, 155
- 48, 56, 128
- 32, 32, 148
- 42, 46, 134
Este problema tiene un error en el planteamiento. Hemos rediseñado el ejercicio para que la respuesta correcta sea el inciso c). Al finalizar la solución, dejaremos una justificación acerca del error.
Solución:
Examinando la figura, tanto \beta como \alpha cumplen la propiedad de ángulos opuestos por el vértice, debido a que las rectas paralelas son cortadas por la misma recta oblicua.
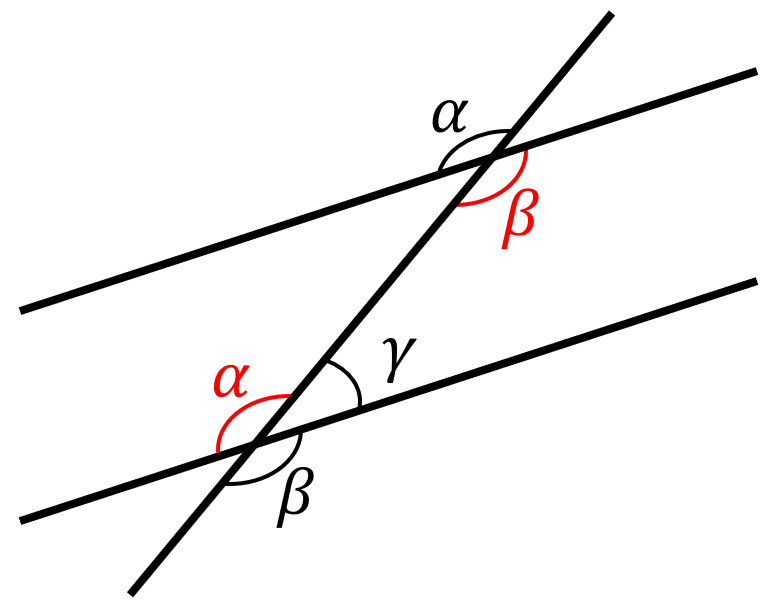
Dicha propiedad establece que \beta =\alpha . Con esto, podemos descartar a los incisos b) y d), porque en los resultados \beta y \alpha son diferentes.
\beta =\alpha \to 6x-14=4x+\frac{4}{3}
Despejamos el valor de x .
6x-4x=14+\frac{4}{3}\to 2x=\frac{46}{3}
\therefore x=\frac{23}{3}
Calculamos el valor de \beta y \alpha .
\alpha =6\left(\frac{23}{3}\right)-14=32°
\beta =4\left(\frac{23}{3}\right)+\frac{4}{3}=32°
Examinando a los incisos, solo el c) inicia con 32, 32. Concluimos que la respuesta correcta es la opción c).
Justificación.
El sistema de ecuaciones original del problema es:
\alpha =6x-34
\beta =4x+20
Aplicamos la propiedad de ángulos opuestos por el vértice.
\alpha =\beta \to 6x-34=4x+20
6x-4x=34+20\to 2x=54
\therefore x=27
Sustituimos:
\alpha =6\left(27\right)-34=128°
\beta =4\left(27\right)+20=128°
Por consecuencia:
\gamma +\beta =180°\to \gamma =180°-\beta
\gamma =180°-128°=52°
La respuesta correcta en este caso sería: 128°, 128°, 52°.
Reactivo 8
Determinar el perímetro del triángulo de acuerdo con la información de la siguiente figura:
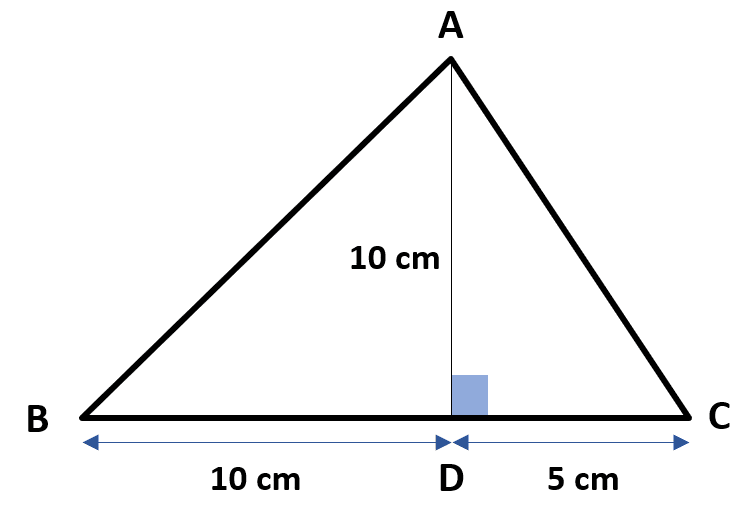
- 10\sqrt{2}+5\sqrt{5}+5
- 10\sqrt{2}+5\sqrt{5}+10
- 10\sqrt{2}+5\sqrt{5}+15
- 10\sqrt{2}+5\sqrt{5}+25
Solución:
En este problema, ni siquiera debemos realizar ningún cálculo para seleccionar la respuesta correcta. Sabemos que el perímetro de cualquier polígono es la suma de sus lados. La figura que se muestra en la imagen es un triángulo de lados AB , BC y CA .
El lado más fácil de obtener es el BC a partir de la suma 10+5=15 \mathrm{c}\mathrm{m} . Ahora, el único inciso que muestra entre sus términos 15 es el inciso c). De igual forma, el cálculo de los otros lados AB y AC se realiza aplicando el teorema de Pitágoras en los triángulos ADB y ADC .
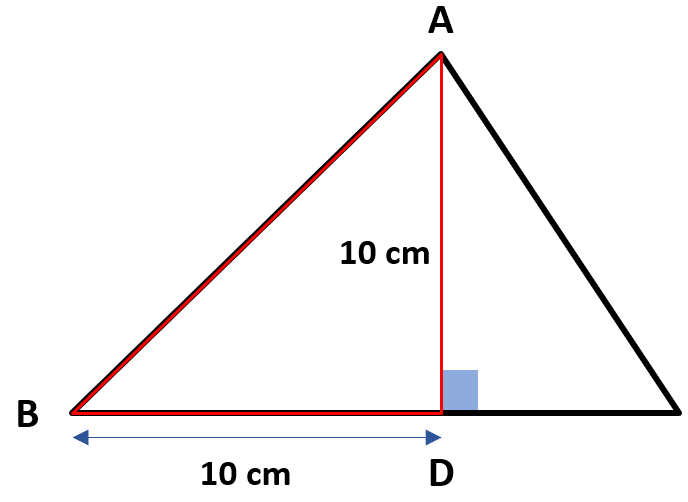
AB=\sqrt{{10}^{2}+{10}^{2}}=\sqrt{2\cdot {10}^{2}}=10\sqrt{2} \mathrm{c}\mathrm{m}
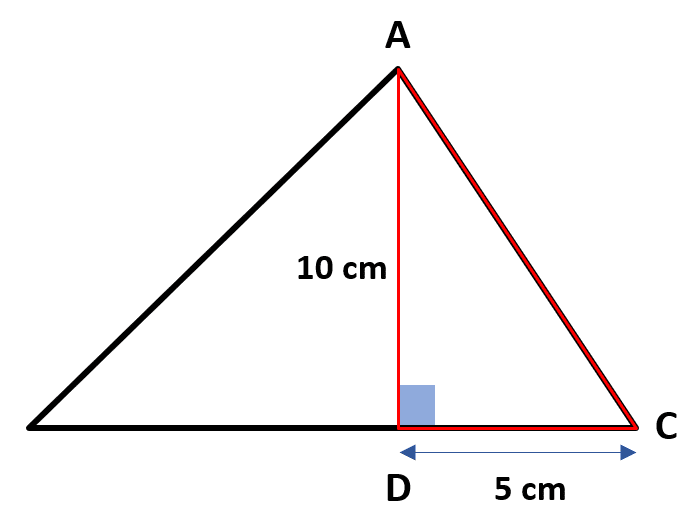
AC=\sqrt{{10}^{2}+{5}^{2}}=\sqrt{{2}^{2}\cdot {5}^{2}+{5}^{2}}=\sqrt{{5}^{2}\cdot \left({2}^{2}+1\right)}=5\sqrt{4+1}=5\sqrt{5} \mathrm{c}\mathrm{m}
Finalmente:
{P}_{ABC}=10\sqrt{2}+5\sqrt{5}+15 \mathrm{c}\mathrm{m}
Reactivo 9
Calcular x si AB=BC=BD .
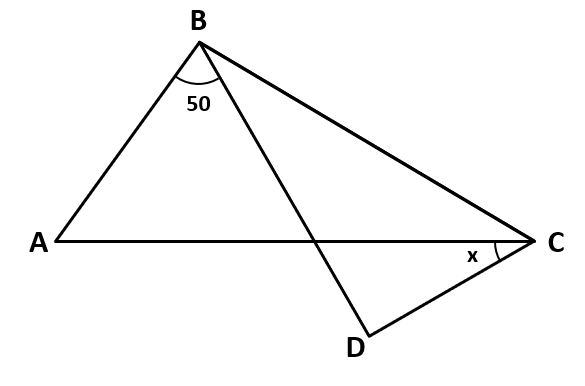
- 25
- 30
- 34
- 50
Solución:
Para resolver el problema, debemos identificar los ángulos en los triángulos y luego relacionarlos hasta encontrar el valor de x . Debido a que ambos triángulos son isósceles, ya que AB=BC=BD dos de los tres ángulos dentro de cada triángulo son iguales.
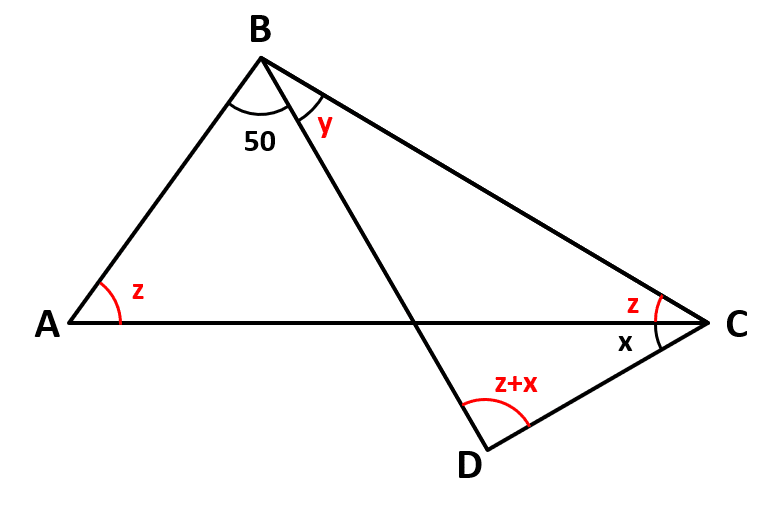
Ahora, aplicamos la propiedad de los triángulos que dice: la suma de los ángulos internos es igual a 180°.
Para el triángulo ABC .
50+y+2z=180\to 2z+y+50=180
Para el triángulo BDC .
y+2\left(x+z\right)=180\to 2z+y+2x=180
Igualamos las ecuaciones, ya que ambas son iguales a 180°.
2z+y+50=2z+y+2x
2x=50\to x=25°
Finalmente, indicamos como respuesta correcta al inciso a).
Reactivo 10
Identificar la fórmula para determinar el número de diagonales que tiene un polígono con n lados.
- D=\frac{n(n-2)}{2}
- D=\frac{n(n+3)}{2}
- D=\frac{n(n+2)}{2}
- D=\frac{n(n-3)}{2}
Solución:
La respuesta a este ejercicio implica que conozcas previamente la ecuación para calcular el número de diagonales en un polígono, debido a que la demostración es de relativa extensión. Vamos a señalar la respuesta correcta y luego demostraremos porqué es esa la expresión.
Cálculo de las diagonales en un polígono:
{D}_{n}=\frac{n\left(n-3\right)}{2}
La respuesta correcta es el inciso d). Por lógica, podríamos seleccionar la d) porque el polígono con menor cantidad de lados es el triángulo n=3 y esta figura no tiene diagonales D=0 . La única expresión que arroja D=0 es la d).
Demostración.
Todo polígono de n lados, tiene también n vértices. Además, desde un vértice cualquiera, se pueden trazar diagonales con el resto de vértices, excepto los dos adyacentes y él mismo. Esto se escribe como n-3 . Si aplicamos esto para los n vértices tenemos: n\left(n-3\right) .
Ahora nos queda dividir entre 2, porque en la expresión n\left(n-3\right) estamos contando diagonales trazadas entre dos vértices en ambos sentidos. Al dividir entre 2 eliminamos la dualidad.
{D}_{n}=\frac{n\left(n-3\right)}{2}


