Guía IPN 2023 Geometría y trigonometría del 11 al 20 resueltos

¡Hola, aspirante! En este tutorial resolveremos la segunda parte de Geometría y trigonometría en la guía IPN. Los reactivos en este post van desde el 11 hasta el 20.

Resuélvelos por tu cuenta antes de mirar la solución. Apóyate de dibujos para ayudarte en la solución, geometría puede ser una asignatura abstracta en algunos casos.

Reactivo 11

¿Cuál es el polígono regular en el cual se pueden trazar 152 diagonales?

1. Endecágono
2. Pentadecágono
3. Octadecágono
4. Eneadecágono

Solución:

Sabemos que la ecuación para calcular las diagonales de un polígono es:

$D=\frac{n\left(n-3\right)}{2}$

Donde $D$ son las diagonales y $n$ los lados del polígono. Sustituimos el total de diagonales y despejamos a $n$ de la ecuación.

$152=\frac{n\left(n-3\right)}{2}\to 304=n\left(n-3\right)$

${n}^{2}-3n-304=0$

Resolvemos aplicando la fórmula de segundo grado.

$n=\frac{-\left(-3\right)\pm \sqrt{{\left(-3\right)}^{2}-4\left(1\right)\left(-304\right)}}{2\left(1\right)}=\frac{3\pm \sqrt{9+1216}}{2}=\frac{3\pm 35}{2}$

Nos quedamos con la solución positiva, ya que no existe tal cosa como aristas negativas.

$n=\frac{3+35}{2}=\frac{38}{2}=19$

El polígono con 19 lados lleva el nombre de eneadecágono.

Concluimos indicando como respuesta correcta al inciso d).

Reactivo 12

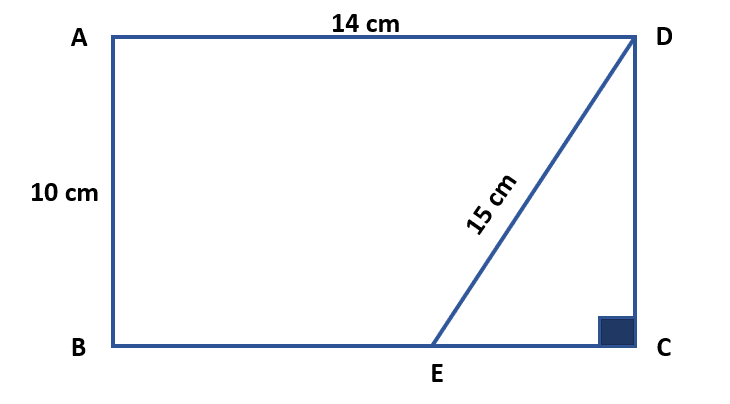
Determinar el perímetro del rectángulo $◻ABED$ usando la información de la siguiente figura.

1. $48-4\sqrt{11}$
2. $48-3\sqrt{11}$
3. $53-5\sqrt{5}$
4. $53-6\sqrt{5}$

Solución:

Examinando a la figura conocemos la longitud de todas las aristas, exceptuando a $\mathrm{B}\mathrm{E}$. El lado $BE$ los podemos calcular como:

$BE=BC-EC$

La longitud de $BC=14 \mathrm{c}\mathrm{m}$ y a $EC$ lo podemos obtener aplicando trigonometría.

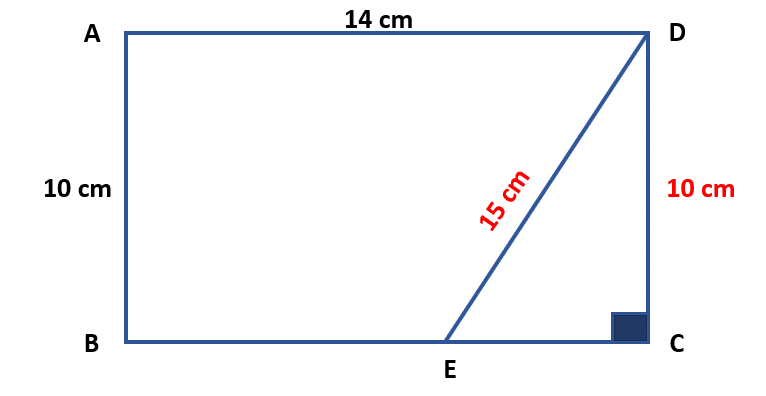
Según el teorema de Pitágoras:

${15}^{2}={10}^{2}+E{C}^{2}\to EC=\sqrt{{15}^{2}-{10}^{2}}$

$EC=\sqrt{125}=5\sqrt{5}$

Sustituimos.

$BE=14-5\sqrt{5}$

El perímetro de $◻ABED$ es:

$◻ABED=53-5\sqrt{5} \mathrm{c}\mathrm{m}$

La respuesta correcta es el inciso c).

Reactivo 13

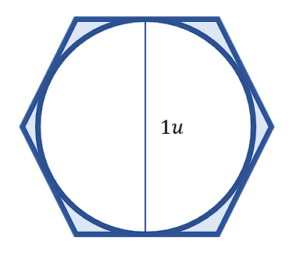
Calcular el área que hay entre el hexágono y la circunferencia.

1. $\frac{1}{4}(\pi -3)$
2. $\frac{1}{8}(\pi -3\sqrt{2})$
3. $\frac{1}{4}(\pi -2\sqrt{3})$
4. $\frac{1}{8}(\pi -4)$

Solución:

El área sombreada se calcula como la resta del área del hexágono con el área del círculo.

${A}_{s}={A}_{h}-{A}_{c}$

El área de un hexágono se obtiene a partir de la siguiente ecuación:

${A}_{h}=\frac{ap}{2}$

Donde $a$ es la apotema y $p$ el perímetro del pentágono. La apotema es la distancia que hay desde el centro de una arista hacia el centro del hexágono.

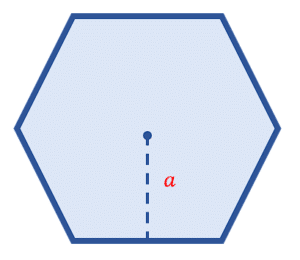
Examinando la figura del enunciado, la apotema es la mitad del diámetro del círculo, es decir: $a=0.5 u$. Por otro lado, la relación entre la apotema y cualquiera de los lados del hexágono es:

$a=\frac{\sqrt{3}l}{2}\to l=\frac{2a}{\sqrt{3}}$

Sustituimos.

$l=\frac{2\left(0.5\right)}{\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$

El perímetro es 6 veces uno de los lados del hexágono.

$p=6\left(\frac{\sqrt{3}}{3}\right)=2\sqrt{3}$

Sustituyendo:

${A}_{h}=\frac{\left(0.5\right)\left(2\sqrt{3}\right)}{2}=\frac{\sqrt{3}}{2}$

El área del círculo se calcula como:

${A}_{c}=\frac{\pi {D}^{2}}{4}=\frac{\pi }{4}$

Finalmente:

${A}_{s}=\frac{\pi }{4}-\frac{\sqrt{3}}{2}=\frac{1}{4}\left(\pi -2\sqrt{3}\right){u}^{2}$

El área sombreada es igual a $\frac{1}{4}\left(\pi -2\sqrt{3}\right){u}^{2}$.

La respuesta correcta es el inciso c).

Reactivo 14

Si el arco $AC={142}^{\circ }$, determinar el valor del ángulo interior $\widehat{B}$.

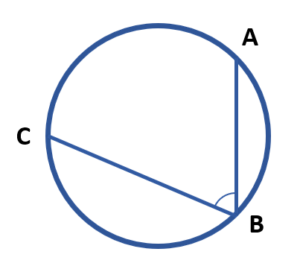
1. 71°
2. 76°
3. 66°
4. 81°

Solución:

Para resolver estos problemas con arcos de circunferencia, ángulos internos y ángulos externos, es necesario que conozcas las expresiones de antemano. Las demostraciones asociadas son bastante complejas y no es práctico desarrollarlas en el examen.

El arco $AC$ se mide respecto al centro de la circunferencia.

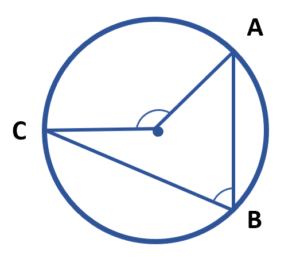
La ecuación que los relaciona es:

$\widehat{B}=\frac{AC}{2}$

Sustituimos:

$\widehat{B}=\frac{142}{2}=71°$

La respuesta correcta es el inciso a).

Reactivo 15

Relacionar cada definición con su concepto.

1. 1D, 2B, 3A, 4C
2. 1D, 2C, 3A, 4B
3. 1B, 2D, 3A, 4C
4. 1B, 2D, 3C, 4A

Solución:

En este caso, es necesario que conozcas cuáles son los elementos de la circunferencia y sus definiciones. Iniciamos con la definición del inciso 1, esta corresponde al arco de una circunferencia: 1D. Descartamos los incisos c) y d).

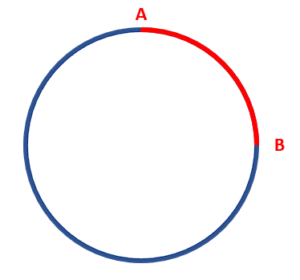
La segunda definición, hace referencia a una cuerda de la circunferencia: 2B.

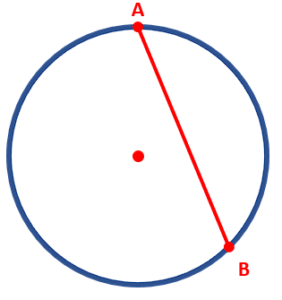
Con esta información: 1D, 2B, … es suficiente para concluir que la respuesta correcta es el inciso a).

Reactivo 16

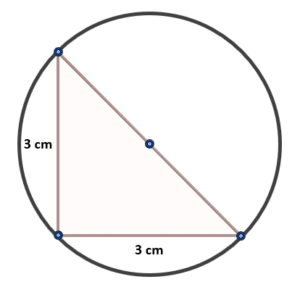
Calcular el diámetro de la circunferencia circunscrita en un triángulo rectángulo con catetos de longitud de 3 cm.

1. $\sqrt{2}$
2. 3
3. $3\sqrt{2}$
4. 9

Solución:

El diámetro de la circunferencia es igual a la hipotenusa del triángulo rectángulo.

$D=\sqrt{{3}^{2}+{3}^{2}}=\sqrt{2\cdot {3}^{2}}=3\sqrt{2}$

El diámetro es igual a $3\sqrt{2}$ centímetros.

La respuesta correcta es el inciso c).

Reactivo 17

Calcular el ángulo $x$ interior a la circunferencia, tal como se muestra en la figura:

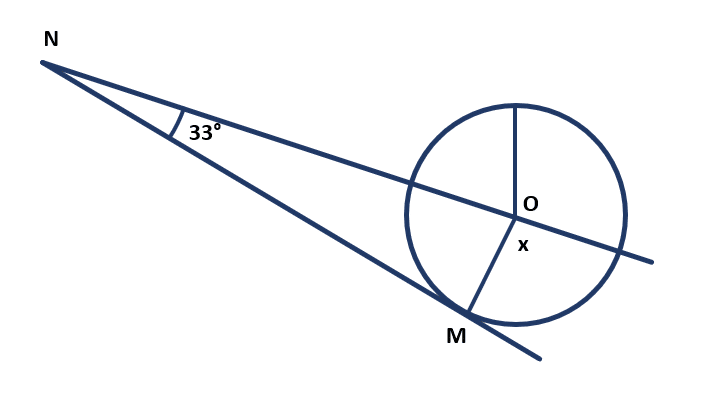
1. 91°
2. 98°
3. 123°
4. 130°

Solución:

La situación planteada en el enunciado, puede asemejarse a la del ángulo circunscrito.

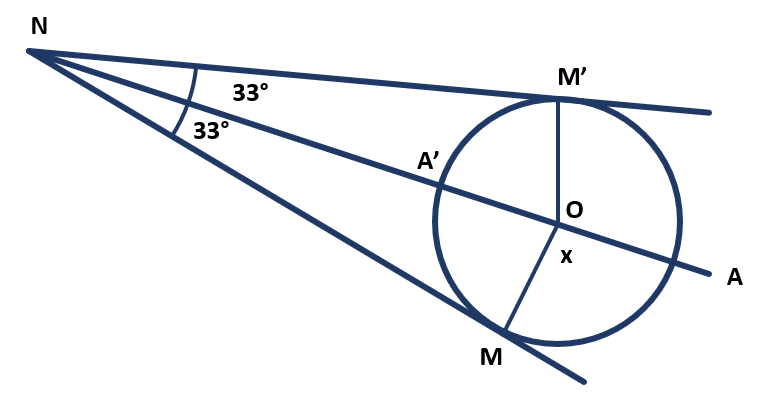
Para esta situación, tenemos una ecuación que relaciona el arco MM’ y el ángulo NMM’.

$NM{M}^{\text{'}}=\frac{MA{M}^{\text{'}}-M{A}^{\text{'}}{M}^{\text{'}}}{2}$

Despejando y sustituyendo nos queda:

$MA{M}^{\text{'}}-M{A}^{\text{'}}{M}^{\text{'}}=2\left(66\right)\to MA{M}^{\text{'}}-M{A}^{\text{'}}{M}^{\text{'}}=132$

$MA{M}^{\text{'}}-M{A}^{\text{'}}{M}^{\text{'}}=132$

En esta ecuación tenemos dos incógnitas, necesitamos encontrar otra que nos permita resolver el problema. Debido a que la circunferencia se divide en dos arcos, la suma de ambos arcos es igual a 360°.

$MA{M}^{\text{'}}-M{A}^{\text{'}}{M}^{\text{'}}=360$

Con esta ecuación, tenemos el siguiente sistema:

$\left\{\begin{array}{c}MA{M}^{\text{'}}-M{A}^{\text{'}}{M}^{\text{'}}=132\\ MA{M}^{\text{'}}-M{A}^{\text{'}}{M}^{\text{'}}=360\end{array}\right.$

Sumando ambas ecuaciones nos queda:

$2MA{M}^{\text{'}}=492\to MA{M}^{\text{'}}=246°$

Ahora, el problema nos pregunta cuál es el valor del ángulo $x$. Este se puede calcular dividiendo al arco $MA{M}^{\text{'}}$ entre 2.

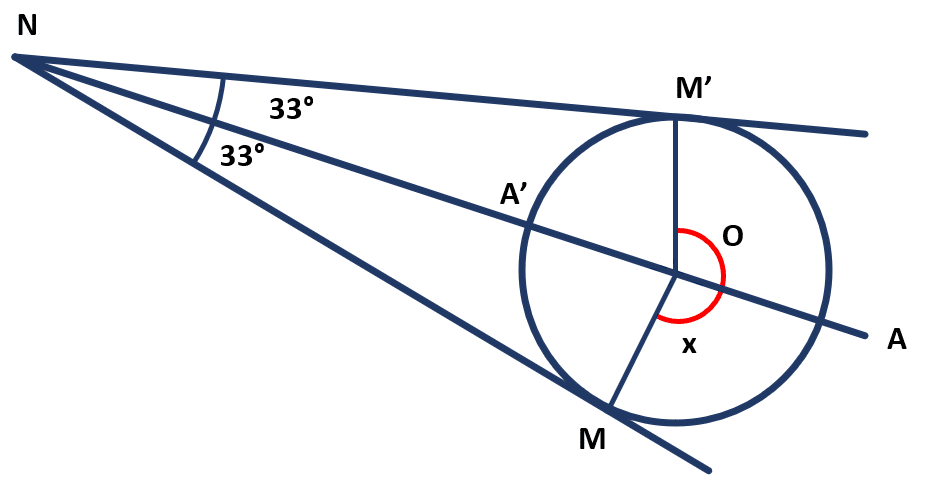
Finalmente:

$x=\frac{246}{2}=123°$

La respuesta correcta es el inciso c).

Reactivo 18

Determinar la amplitud del ángulo $\mathrm{\angle }BDC$ si el ángulo $\mathrm{\angle }BAC={48}^{\circ }$.

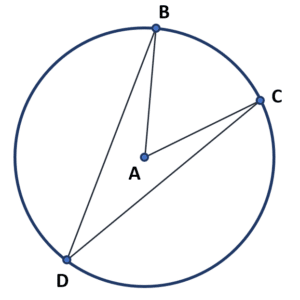
1. 14°
2. 24°
3. 28°
4. 48°

Solución:

El ángulo solicitado se calcula con la ecuación de ángulo inscrito.

$\mathrm{\angle }BDC=\frac{\mathrm{\angle }BAC}{2}=\frac{48°}{2}=24°$

El ángulo inscrito es igual a 24°.

La respuesta correcta es el inciso b).

Reactivo 19

Reducir la expresión:

$\frac{1-{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\beta }{(1-\mathrm{s}\mathrm{e}\mathrm{n}\beta )(1+\mathrm{s}\mathrm{e}\mathrm{n}\beta )}$

1. ${\mathrm{s}\mathrm{e}\mathrm{c}}^{2}\beta$
2. ${\mathrm{t}\mathrm{a}\mathrm{n}}^{2}\beta$
3. ${\mathrm{c}\mathrm{o}\mathrm{t}}^{2}\beta$
4. ${\mathrm{s}\mathrm{e}\mathrm{n}}^{2}\beta$

Solución:

Para simplificar la expresión trigonométrica, empleamos la identidad pitagórica.

${\mathrm{sin}}^{2}\beta +{\mathrm{cos}}^{2}\beta =1$

Simplificamos el producto de conjugados en el denominador.

$\frac{1-{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\beta }{(1-\mathrm{s}\mathrm{e}\mathrm{n}\beta )(1+\mathrm{s}\mathrm{e}\mathrm{n}\beta )}=\frac{1-{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\beta }{1-{\mathrm{s}\mathrm{i}\mathrm{n}}^{2}\beta }$

Sustituimos a $1-{\mathrm{s}\mathrm{i}\mathrm{n}}^{2}\beta$ por ${\mathrm{cos}}^{2}\beta$.

$\frac{1-{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\beta }{1-{\mathrm{s}\mathrm{i}\mathrm{n}}^{2}\beta }=\frac{1-{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\beta }{{\mathrm{cos}}^{2}\beta }=\frac{1}{{\mathrm{cos}}^{2}\beta }-1$

$\therefore {\mathrm{sec}}^{2}\beta -1$

Ahora, recurrimos a la identidad pitagórica en términos de la secante y la tangente.

${\mathrm{sec}}^{2}\beta ={\mathrm{tan}}^{2}\beta +1\to {\mathrm{sec}}^{2}\beta -1={\mathrm{tan}}^{2}\beta$

Finalmente:

${\mathrm{sec}}^{2}\beta -1={\mathrm{tan}}^{2}\beta$

$\frac{1-{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\beta }{(1-\mathrm{s}\mathrm{e}\mathrm{n}\beta )(1+\mathrm{s}\mathrm{e}\mathrm{n}\beta )}={\mathrm{tan}}^{2}\beta$

Comparando el resultado con los incisos, concluimos que la respuesta correcta es el b).

Reactivo 20

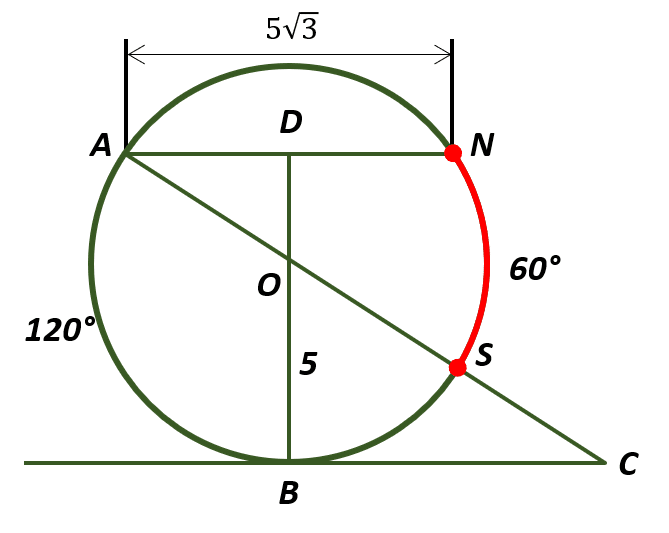
Calcular la longitud $AN$ y el arco $\widehat{NS}$ si se conoce $OB=5$, $\widehat{AB}=120$ y $AN\parallel BC$ como muestra la figura:

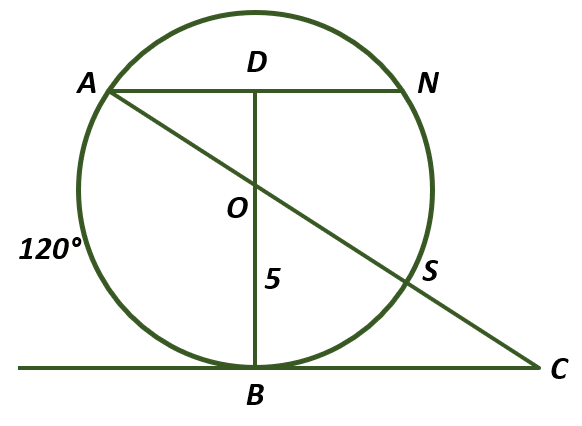
1. $4,{30}^{\circ }$
2. $8,{60}^{\circ }$
3. $5\sqrt{3},{60}^{\circ }$
4. $4\sqrt{2},{30}^{\circ }$

Solución:

La solución de este problema implica el uso inteligente de las relaciones entre los ángulos notables de una circunferencia y los triángulos que se forman en ella. Iniciamos calculando el arco $NS$. Debido a que el segmento $CA$ pasa por el centro, el triángulo $ABC$ es igual al triángulo $ACN$.

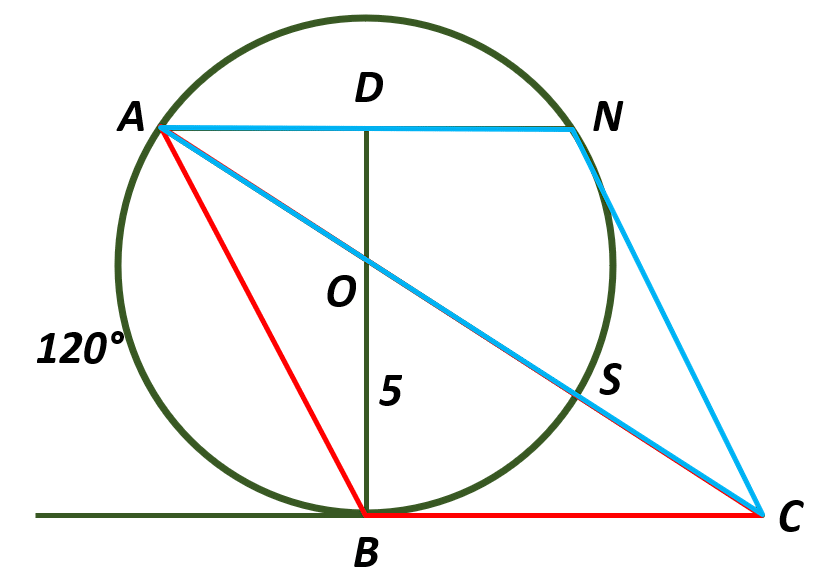
Como consecuencia de esto, los arcos $AB=120°$ y $AN$ son iguales, mientras que $BS=SN$. Por otra parte, la suma de los 4 arcos debe ser igual a 360°.

$AB+AN+BS+SN=360°$

Sustituimos $BS=NS$.

$120+120+2NS=360\to NS=60°$

El arco $NS$ es igual a 60°. Debido a que el triángulo $AON$ coincide con el arco $AN$, sabemos que el ángulo $\widehat{O}$ es igual al arco $AN$.

$\widehat{O}=AN=120°$

Vemos que se forma un triángulo isósceles en la circunferencia. Conocemos la longitud de los lados semejantes, debido a que corresponden con el radio de la circunferencia.

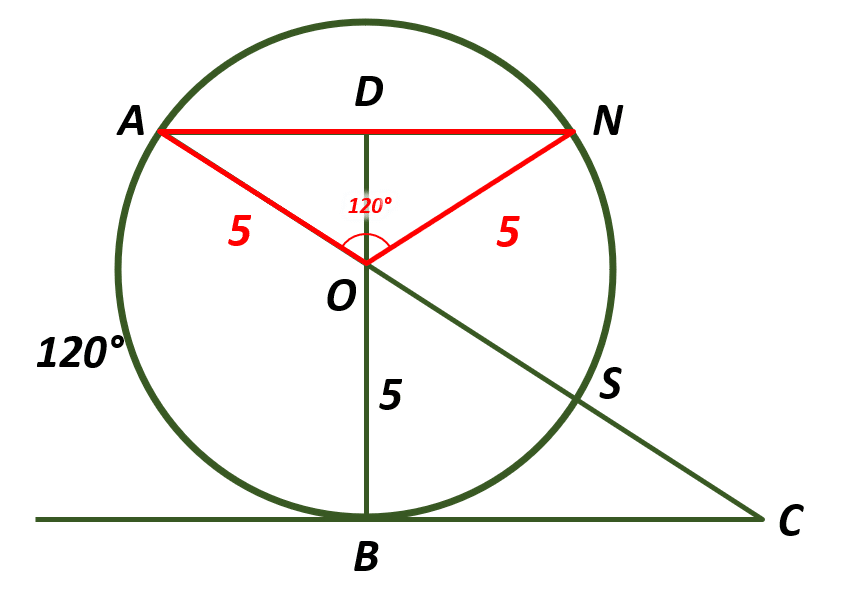
El lado $AN$ se puede calcular aplicando la ley del coseno.

$A{N}^{2}={5}^{2}+{5}^{2}-2\left(5\right)\left(5\right)\mathrm{cos}120$

$A{N}^{2}=50-50\left(-\frac{1}{2}\right)=75$

$AN=\sqrt{75}=5\sqrt{3}$

Finalmente:

$AN=5\sqrt{3}, \widehat{NS}=60°$

La respuesta correcta es el inciso c).