¡Saludos, aspirante! En este tutorial vamos a resolver la tercera parte de Geometría y trigonometría, correspondiente a los reactivos desde el 21 al 30 en la guía del IPN 2023.

Recuerda tomar descansos entre grupos de reactivos. Es importante que analices el procedimiento para buscar alternativas más rápidas.
Reactivo 21
Identificar los valores de x expresados en términos de n=0, 1, 2, 3,\dots que reproducen el mínimo de la función g\left(x\right)=\mathrm{c}\mathrm{o}\mathrm{s}\left(x\right)=-1 .
- x=\left(2n-\frac{1}{2}\right)\pi
- x=(2n+1)\frac{\pi }{2}
- x=(2n-1)\frac{\pi }{2}
- x=(2n+1)\pi
Solución:
Sabemos que la función coseno es igual a -1 cuando el argumento es igual a \pi . Debido a que solo en \pi el coseno es igual a -1, obtendremos dicho resultado cada 2n\pi veces. Como n inicia en cero, le debemos sumar \pi para obtener dicho resultado cuando n=0 .
x=2n\pi +\pi =\left(2n+1\right)\pi
Desarrollando esta sucesión:
x=\pi , 3\pi ,5\pi , 7\pi , \dots
El coseno vale -1 para múltiplos impares de \pi .
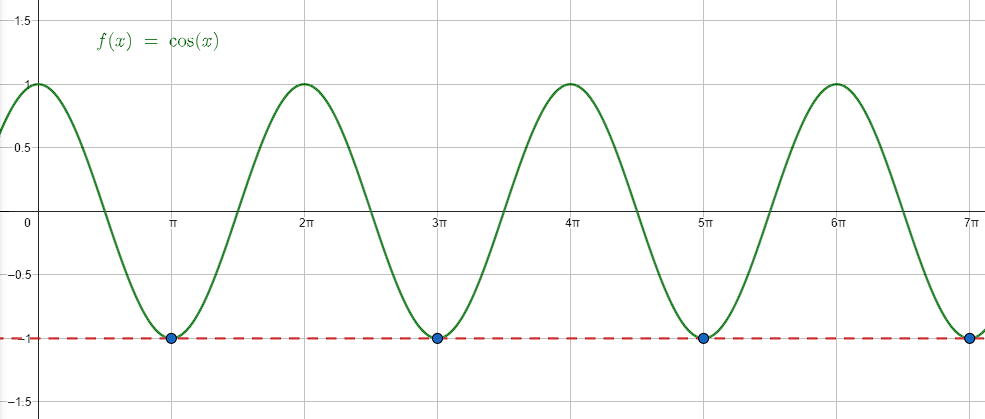
La respuesta correcta es el inciso d).
Reactivo 22
La identidad trigonométrica ____ es equivalente a:
\frac{{\mathrm{s}\mathrm{e}\mathrm{n}}^{3}\left(\alpha \right)}{\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)}+\frac{1}{2}\mathrm{s}\mathrm{e}\mathrm{n}\left(2\alpha \right)
- \mathrm{tan}\left(\alpha \right)
- \mathrm{s}\mathrm{e}\mathrm{c}\left(\alpha \right)
- \mathrm{c}\mathrm{o}\mathrm{t}\left(\alpha \right)
- \mathrm{c}\mathrm{o}\mathrm{t}\left(\alpha \right)\mathrm{t}\mathrm{a}\mathrm{n}\left(\alpha \right)
Solución:
Debemos simplificar la expresión trigonométrica del enunciado, aplicando las identidades trigonométricas que sean necesarias. Iniciamos separando al seno como {\mathrm{s}\mathrm{e}\mathrm{n}}^{2}\left(\alpha \right)\mathrm{sin}\left(\alpha \right) y al seno del ángulo doble lo sustituimos por:
\mathrm{sen}\left(2\alpha \right)=2\mathrm{sin}\alpha \mathrm{cos}\alpha
\frac{{\mathrm{s}\mathrm{e}\mathrm{n}}^{3}\left(\alpha \right)}{\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)}+\frac{1}{2}\mathrm{sen}\left(2\alpha \right)=\frac{{\mathrm{s}\mathrm{e}\mathrm{n}}^{2}\left(\alpha \right)\mathrm{sin}\left(\alpha \right)}{\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)}+\frac{1}{2}2\mathrm{sin}\alpha \mathrm{cos}\alpha ={\mathrm{sen}}^{2}\left(\alpha \right)\frac{\mathrm{sin}\left(\alpha \right)}{\mathrm{cos}\left(\alpha \right)} +\mathrm{sin}\alpha \mathrm{cos}\alpha
Extraemos como factor común al seno.
{\mathrm{sen}}^{2}\left(\alpha \right)\frac{\mathrm{sin}\left(\alpha \right)}{\mathrm{cos}\left(\alpha \right)} +\mathrm{sin}\alpha \mathrm{cos}\alpha =\left({\mathrm{sen}}^{2}\left(\alpha \right)\frac{1}{\mathrm{cos}\left(\alpha \right)} +\mathrm{cos}\alpha \right)\mathrm{sin}\left(\alpha \right)
Resolvemos la suma de fracciones.
\left({\mathrm{sen}}^{2}\left(\alpha \right)\frac{1}{\mathrm{cos}\left(\alpha \right)} +\mathrm{cos}\alpha \right)\mathrm{sin}\left(\alpha \right)=\frac{{\mathrm{sen}}^{2}\left(\alpha \right) +{\mathrm{cos}}^{2}\alpha }{\mathrm{cos}\left(\alpha \right)}\mathrm{sin}\left(\alpha \right)
Sustituimos {\mathrm{sen}}^{2}\left(\alpha \right) +{\mathrm{cos}}^{2}\alpha =1 .
\frac{{\mathrm{sen}}^{2}\left(\alpha \right) +{\mathrm{cos}}^{2}\alpha }{\mathrm{cos}\left(\alpha \right)}\mathrm{sin}\left(\alpha \right)=\frac{1}{\mathrm{cos}\left(\alpha \right)}\mathrm{sin}\left(\alpha \right)
Finalmente:
\frac{1}{\mathrm{cos}\left(\alpha \right)}\mathrm{sin}\left(\alpha \right)=\mathrm{tan}\alpha
\frac{{\mathrm{s}\mathrm{e}\mathrm{n}}^{3}\left(\alpha \right)}{\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)}+\frac{1}{2}\mathrm{sen}\left(2\alpha \right)=\mathrm{tan}\alpha
Concluimos indicando como respuesta correcta la opción a).
Reactivo 23
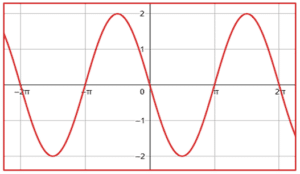
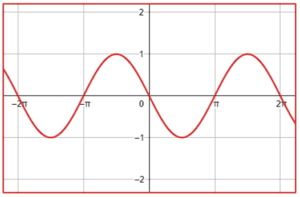
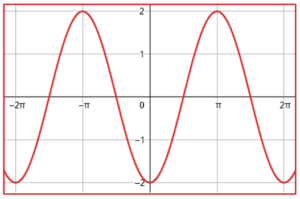
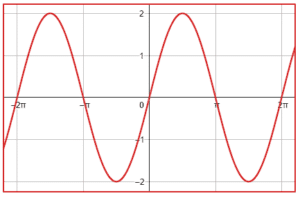
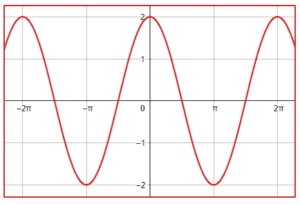
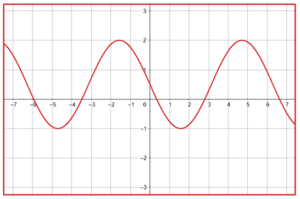
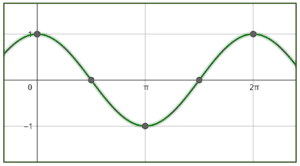
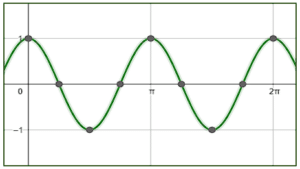
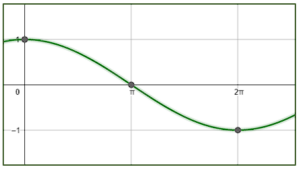
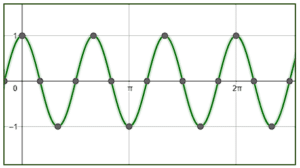
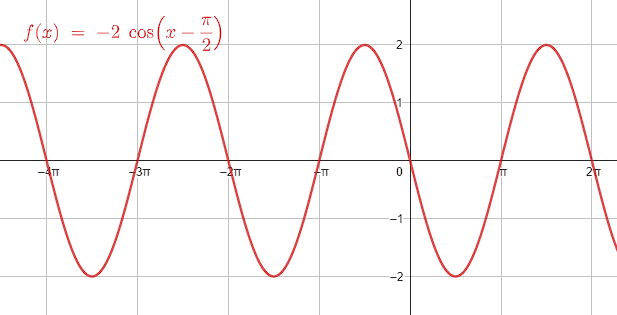
¿Qué gráfica corresponde a la función f\left(x\right)=-2\mathrm{c}\mathrm{o}\mathrm{s}\left(x-\frac{\pi }{2}\right) ?
Solución:
Examinando la expresión trigonométrica dada por el enunciado, observamos que tiene como amplitud 2, por lo tanto, descartamos a los incisos d y c porque la amplitud de estas funciones sinusoidales es 1.
El coseno desplazado -\frac{\pi }{2} es igual al seno del ángulo.
-2\mathrm{cos}\left(x-\frac{\pi }{2}\right)=-2\mathrm{sin}\left(x\right)
La función del seno inicia en cero, examinando a los incisos a y b, la única gráfica que muestra a una función que inicia desde cero es la a). Además, observamos que es idéntica al seno pero invertida, esto es por el signo negativo que la multiplica.
Reactivo 24
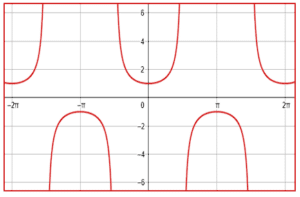
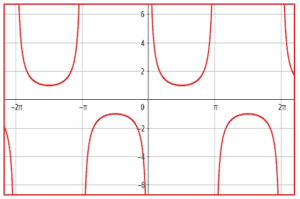
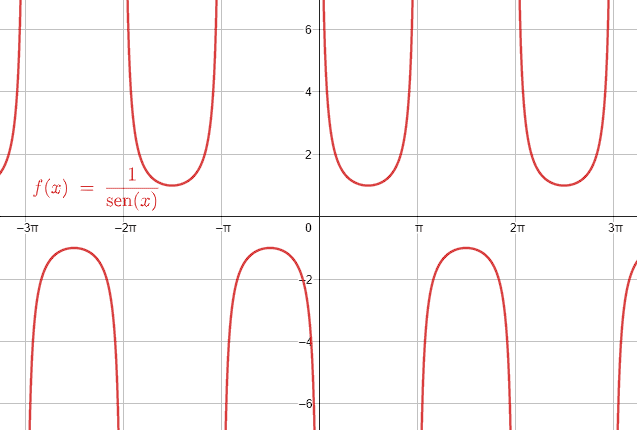
Identificar la gráfica que corresponde a la función \frac{1}{\mathrm{s}\mathrm{e}\mathrm{n}\left(\theta \right)} .
Solución:
Esta pregunta puede responderse de forma directa si conoces la teoría y fundamentos de las gráficas para las funciones trigonométricas, \frac{1}{\mathrm{s}\mathrm{e}\mathrm{n}\left(\theta \right)} es la cosecante de theta. La respuesta correcta es el inciso d).
Aun así, te dejaré un truco para identificar cuál es la gráfica de \frac{1}{\mathrm{s}\mathrm{e}\mathrm{n}\left(\theta \right)} . Sustituimos \theta =0 y examinamos qué sucede con el resultado.
\frac{1}{\mathrm{s}\mathrm{e}\mathrm{n}\left(0\right)}=\frac{1}{0}=\infty
La función se indetermina para \theta =0 . De entre las gráficas, la única que se indetermina en este valor es la d).
Reactivo 25
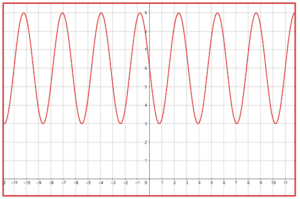
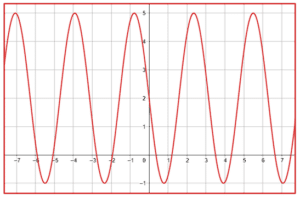
Señalar la gráfica que corresponde a la función y=6-3\mathrm{s}\mathrm{e}\mathrm{n}2x .
Solución:
Para identificar la gráfica correcta debemos fijarnos de en tres detalles: que el punto de equilibrio sea 6, que el punto más alto sea 9 y el más bajo 3 (porque la amplitud de la senoidal es 3) y que complete un ciclo entre 0 y \pi .
Teniendo en cuenta el primer aspecto, la única gráfica con punto de equilibrio en 6 es la del inciso b). Si examinamos los otros dos aspectos, vemos que también los cumple: el rango está definido entre 3 y 9; da una oscilación completa entre 0 y \pi .
La respuesta correcta es el inciso b).
Reactivo 26
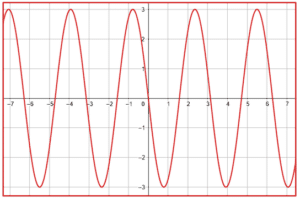
Elegir la gráfica que corresponde a la función f\left(x\right)=\mathrm{c}\mathrm{o}\mathrm{s}\left(2x\right) .
Solución:
Debido a que la función del enunciado es el coseno del ángulo doble, debemos tener en cuenta las siguientes características: que el rango sea entre -1 y 1, que inicie en +1 y que haga un ciclo entre 0 y \pi .
Todos los incisos cumplen con las dos primeras características, pero solo el inciso b) cumple con las tres. Concluimos entonces que la respuesta correcta es la opción b).
Reactivo 27
¿Cuál es la función equivalente a la identidad que se muestra a continuación?
\frac{\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta }{\mathrm{tan}\beta \cdot \mathrm{sen}\beta +\mathrm{cos}\beta }
- \mathrm{s}\mathrm{e}\mathrm{n}\beta
- \mathrm{c}\mathrm{o}\mathrm{s}\beta
- \mathrm{t}\mathrm{a}\mathrm{n}\beta
- \mathrm{s}\mathrm{e}\mathrm{c}\beta
Solución:
Iniciamos Descomponiendo a la tangente como \mathrm{tan}\beta =\frac{\mathrm{sen}\beta }{\mathrm{cos}\beta } .
\frac{\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta }{\mathrm{tan}\beta \cdot \mathrm{sen}\beta +\mathrm{cos}\beta }=\frac{\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta }{\frac{\mathrm{sen}\beta }{\mathrm{cos}\beta }\cdot \mathrm{sen}\beta +\mathrm{cos}\beta }
Simplificamos.
\frac{\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta }{\frac{\mathrm{sen}\beta }{\mathrm{cos}\beta }\cdot \mathrm{sen}\beta +\mathrm{cos}\beta }=\frac{\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta }{\frac{{\mathrm{sen}}^{2}\beta +{\mathrm{cos}}^{2}\beta }{\mathrm{cos}\beta }}
Sustituimos {\mathrm{sen}}^{2}\beta +{\mathrm{cos}}^{2}\beta =1 .
\frac{\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta }{\frac{{\mathrm{sen}}^{2}\beta +{\mathrm{cos}}^{2}\beta }{\mathrm{cos}\beta }}=\frac{\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta }{\frac{1}{\mathrm{cos}\beta }}
\frac{\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta }{\frac{1}{\mathrm{cos}\beta }}=\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta \mathrm{cos}\beta
Sustituimos a {\mathrm{sec}}^{2}\beta -1={\mathrm{tan}}^{2}\beta .
\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta \mathrm{cos}\beta ={\mathrm{tan}}^{2}\beta \cdot \mathrm{cot}\beta \cdot \mathrm{cos}\beta
Simplificamos {\mathrm{tan}}^{2}\beta \cdot \mathrm{cot}\beta =\mathrm{tan}\beta
{\mathrm{tan}}^{2}\beta \cdot \mathrm{cot}\beta \cdot \mathrm{cos}\beta =\mathrm{tan}\beta \cdot \mathrm{cos}\beta
Descomponemos a la tangente y simplificamos.
\mathrm{tan}\beta \cdot \mathrm{cos}\beta =\frac{\mathrm{sen}\beta }{\mathrm{cos}\beta }\cdot \mathrm{cos}\beta =\mathrm{sen}\beta
Finalmente:
\frac{\left({\mathrm{sec}}^{2}\beta -1\right)\mathrm{cot}\beta }{\mathrm{tan}\beta \cdot \mathrm{sen}\beta +\mathrm{cos}\beta }=\mathrm{sen}\beta
Examinando a los incisos, indicamos a la opción a) como la respuesta correcta.
Reactivo 28
La expresión ____ es igual a la identidad trigonométrica:
{\mathrm{cot}}^{2}\left(\theta \right)-{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\theta \right)=
- {\mathrm{c}\mathrm{o}\mathrm{t}}^{2}\left(\theta \right)\cdot {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\theta \right)
- {\mathrm{c}\mathrm{o}\mathrm{t}}^{2}\left(\theta \right)+{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\theta \right)
- {\mathrm{t}\mathrm{a}\mathrm{n}}^{2}\left(\theta \right)\cdot {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\theta \right)
- {\mathrm{cot}}^{2}\left(\theta \right)-{\mathrm{cos}}^{2}\left(\theta \right)
Solución:
Sustituimos a la cotangente cuadrado por: {\mathrm{cot}}^{2}\left(\theta \right)=\frac{{\mathrm{cos}}^{2}\left(\theta \right)}{{\mathrm{sin}}^{2}\left(\theta \right)} .
{\mathrm{cot}}^{2}\left(\theta \right)-{\mathrm{cos}}^{2}\left(\theta \right)=\frac{{\mathrm{cos}}^{2}\left(\theta \right)}{{\mathrm{sin}}^{2}\left(\theta \right)}-{\mathrm{cos}}^{2}\left(\theta \right)
Extraemos factor común al coseno cuadrado.
\frac{{\mathrm{cos}}^{2}\left(\theta \right)}{{\mathrm{sin}}^{2}\left(\theta \right)}-{\mathrm{cos}}^{2}\left(\theta \right)=\left(\frac{1}{{\mathrm{sin}}^{2}\left(\theta \right)}-1\right){\mathrm{cos}}^{2}\left(\theta \right)
Sustituimos al inverso del seno cuadrado por la cosecante cuadrado.
\left(\frac{1}{{\mathrm{sin}}^{2}\left(\theta \right)}-1\right){\mathrm{cos}}^{2}\left(\theta \right)=\left({\mathrm{csc}}^{2}\left(\theta \right)-1\right){\mathrm{cos}}^{2}\left(\theta \right)
Aplicamos la identidad pitagórica en términos de la cotangente y cosecante.
{\mathrm{csc}}^{2}\left(\theta \right)=1+{\mathrm{cot}}^{2}\left(\theta \right)\to {\mathrm{cot}}^{2}\left(\theta \right)={\mathrm{csc}}^{2}\left(\theta \right)-1
Sustituyendo nos queda:
{\mathrm{cot}}^{2}\left(\theta \right){\mathrm{cos}}^{2}\left(\theta \right)
Finalmente:
{\mathrm{cot}}^{2}\left(\theta \right)-{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\theta \right)={\mathrm{cot}}^{2}\left(\theta \right){\mathrm{cos}}^{2}\left(\theta \right)
La respuesta correcta es el inciso a).
Reactivo 29
Identificar la expresión equivalente a
\frac{{\mathrm{s}\mathrm{e}\mathrm{n}}^{2}x-1}{{\left({\mathrm{c}\mathrm{o}\mathrm{t}}^{2}x+1\right)}^{-1/2}}
- \frac{\mathrm{cos}x}{\mathrm{tan}x}
- -\frac{\mathrm{cos}x}{\mathrm{cot}x}
- -\mathrm{c}\mathrm{o}\mathrm{s}x\cdot \mathrm{c}\mathrm{o}\mathrm{t}x
- \mathrm{cos}x\cdot \mathrm{tan}x
Solución:
Para resolver este problema, empleamos las identidades pitagóricas que se muestran a continuación:
{\mathrm{csc}}^{2}\left(x\right)=1+{\mathrm{cot}}^{2}\left(x\right)
{\mathrm{sen}}^{2}x+{\mathrm{cos}}^{2}x=1\to {\mathrm{sen}}^{2}x-1=-{\mathrm{cos}}^{2}x
Sustituimos en la expresión del enunciado.
\frac{{\mathrm{sen}}^{2}x-1}{{\left({\mathrm{cot}}^{2}x+1\right)}^{-1/2}}=\frac{-{\mathrm{cos}}^{2}x}{{\left({\mathrm{csc}}^{2}\left(x\right)\right)}^{-1/2}}=-{\mathrm{cos}}^{2}x{\left({\mathrm{csc}}^{2}\left(x\right)\right)}^{1/2}
Expresamos a la potencia fraccionaria como una raíz cuadrada.
-{\mathrm{cos}}^{2}x{\left({\mathrm{csc}}^{2}\left(x\right)\right)}^{\frac{1}{2}}=-{\mathrm{cos}}^{2}x\sqrt{{\mathrm{csc}}^{2}\left(x\right)}=-\mathrm{csc}x{\mathrm{cos}}^{2}x
Expresamos a la cosecante como el inverso del seno.
-\mathrm{csc}x{\mathrm{cos}}^{2}x=-\frac{1}{\mathrm{sin}x}{\mathrm{cos}}^{2}x=-\frac{\mathrm{cos}x}{\mathrm{sin}x}\mathrm{cos}x
Finalmente:
-\frac{\mathrm{cos}x}{\mathrm{sin}x}\mathrm{cos}x=-\mathrm{cot}x\mathrm{cos}x
\frac{{\mathrm{s}\mathrm{e}\mathrm{n}}^{2}x-1}{{\left({\mathrm{c}\mathrm{o}\mathrm{t}}^{2}x+1\right)}^{-1/2}}=-\mathrm{cot}x\mathrm{cos}x
Indicamos como respuesta correcta al inciso c).
Reactivo 30
Simplificar la expresión:
\frac{1+\mathrm{csc}z}{\mathrm{cot}z+\mathrm{cos}z}
- \mathrm{sen}z
- \mathrm{sec}z
- \mathrm{csc}z
- \mathrm{cos}z
Solución:
Sustituimos a la cosecante y a la cotangente por sus equivalentes en términos del seno y coseno.
\frac{1+\mathrm{csc}z}{\mathrm{cot}z+\mathrm{cos}z}=\frac{1+\frac{1}{\mathrm{sin}z}}{\frac{\mathrm{cos}z}{\mathrm{sin}z}+\mathrm{cos}z}=\frac{\frac{\mathrm{sin}z+1}{\mathrm{sin}z}}{\frac{\mathrm{cos}z+\mathrm{sin}z\mathrm{cos}z}{\mathrm{sin}z}}
Simplificando:
\frac{\frac{\mathrm{sin}z+1}{\mathrm{sin}z}}{\frac{\mathrm{cos}z+\mathrm{sin}z\mathrm{cos}z}{\mathrm{sin}z}}=\frac{\mathrm{sin}z+1}{\mathrm{cos}z+\mathrm{sin}z\mathrm{cos}z}=\frac{\mathrm{sin}z+1}{\left(1+\mathrm{sin}z\right)\mathrm{cos}z}
\frac{\mathrm{sin}z+1}{\left(1+\mathrm{sin}z\right)\mathrm{cos}z}=\frac{1}{\mathrm{cos}z}=\mathrm{sec}z
Finalmente:
\frac{1+\mathrm{csc}z}{\mathrm{cot}z+\mathrm{cos}z}=\mathrm{sec}z
La respuesta correcta es el inciso b).