¡Felicidades aspirante! Llegamos a la quinta y última parte del simulacro de matemáticas para el área de Ciencias Médico Biológicas del Instituto Politécnico Nacional.

Vamos a resolver 10 reactivos de Probabilidad y Estadística. Para que te vaya bien, recuerda repasar los temas de esta asignatura. Tómate descansos entre reactivos y trata de resolverlos por tu cuenta antes de ver la solución.
Ejercicios de Matemáticas
¡Felicidades por llegar a esta última parte del simulacro, aspirante! Accede al contenido gratuito del examen en la zona de materiales del IPN, donde hacemos maratones de reactivos y lives resolviendo guías del examen.
Reactivo 41
En estadística descriptiva, la moda es un parámetro de tendencia central que caracteriza al evento…
- Menos común de una población en estudio
- Más común de una población en estudio
- Que más se desvía de la media
- Que representa una ocurrencia mayor a los 3 \sigma
Solución:
En estadística descriptiva existen numerosos parámetros que nos permiten caracterizar la información que estamos manejando. Las medidas de tendencia central permiten indicar una característica resaltante en el conjunto de datos.
Para el caso de la moda, podemos indicar cuál es el elemento que predomina o que más se repite en el conjunto de datos. Dicho de otra forma, la moda es un parámetro de tendencia central que indica cuál es el elemento más común de una población en estudio.
Teniendo en cuenta lo anterior y examinando los incisos, concluimos que la respuesta correcta se encuentra en el inciso b).
Reactivo 42
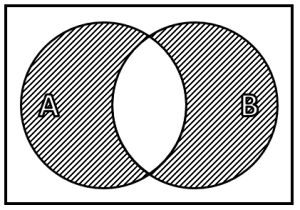
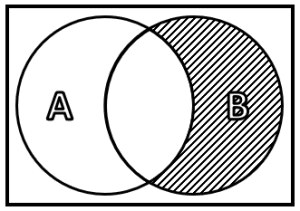
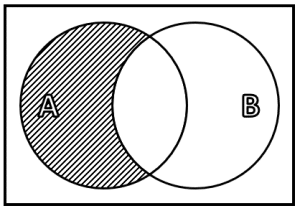
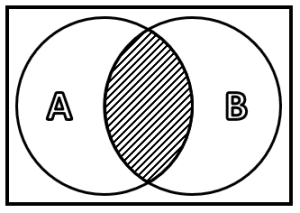
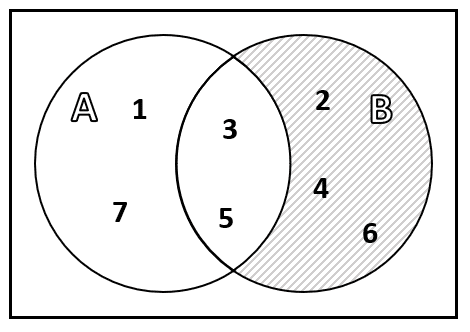
¿Cuál de los siguientes diagramas de Venn representa la operación A\cap {B}^{C} ?
Solución:
Para resolver este problema tenemos dos opciones: aplicando operaciones y propiedades de los conjuntos o de forma gráfica paso por paso. La primera opción es la más óptima, pero si no tienes un excelente dominio resolviendo operaciones entre conjuntos, puede llegar a complicarse.
La opción más recomendada es la de utilizar diagramas de Venn para llegar a la solución, es más sencillo y evitarás confusiones. Primero, comenzamos por identificar quienes son los conjuntos A y {B}^{c} .
El conjunto A .
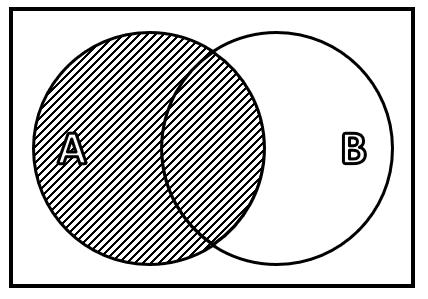
El complemento del conjunto B .
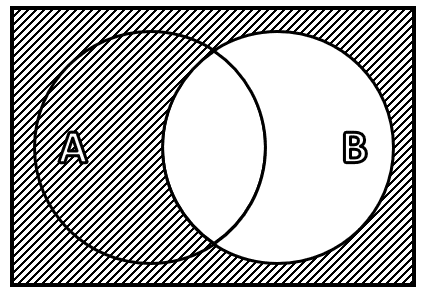
La intersección de estos conjuntos corresponde a sus elementos comunes, es decir:
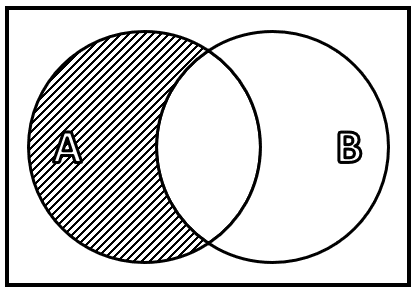
Comparando con las opciones, concluimos que la respuesta correcta es la c).
Reactivo 43
Calcule cuántos códigos de 7 símbolos se pueden formar con las letras A, B, C, D, E, F y G.
- 4040
- 5050
- 5040
- 4050
Solución:
Para resolver cualquier problema de conteo, debemos responder dos preguntas: ¿importa el orden? y ¿los elementos se repiten? Es claro que, si la intención es formar códigos, no será igual la palabra ABCDEFG que la palabra ABCDEGF, por tanto, estamos tratando con permutaciones/variaciones.
Ahora, en ningún momento se indica que es posible repetir las letras, incluso el enunciado menciona que esas son las letras que tenemos para formar el código, en consecuencia, no es posible repetir. Se trata de una permutación debido a que intervienen todos los elementos.
{P}_{m}=m!
En este caso m=7 . Sustituyendo:
{P}_{7}=7!=5040
Se pueden crear 5040 códigos distintos con las letras de la A hasta la G.
Concluimos indicando como respuesta correcta la opción c).
Reactivo 44
La siguiente tabla de datos, muestra la cantidad de estudiantes que obtuvieron calificaciones entre 1 y 10 puntos.
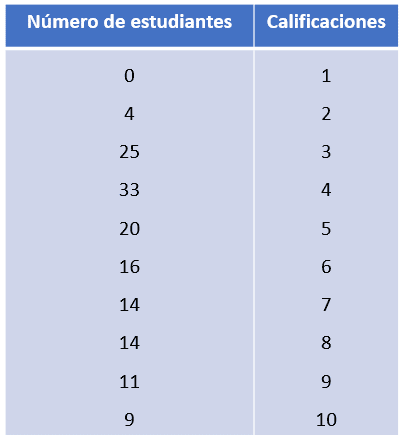
Calcular la probabilidad de que un estudiante haya obtenido un 10 en el examen.
- 8%
- 3%
- 16%
- 99%
Solución:
Debemos recordar la definición operacional de probabilidad clásica: la probabilidad P de que ocurra cierto evento A , se escribe como P\left(A\right) y se calcula como el cociente entre los casos favorables al evento A y el total de casos.
P\left(A\right)=\frac{A}{U}
Por tanto, debemos identificar en la tabla los estudiantes que obtuvieron un 10 y el total de estudiantes.
\mathrm{E}\mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{ }10=9
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{s}=4+25+33+20+16+14+14+11+9=146
Probabilidad de que un estudiante haya obtenido un 10:
P\left(10\right)=\frac{9}{146}=6.16\%
Comparando con las opciones, indicamos como correcta la c).
Reactivo 45
La ___________ entre dos conjuntos A y B , se forma por todos los elementos de A que no se encuentran en B .
- Unión
- Intersección
- Diferencia simétrica
- Diferencia
Solución:
Para completar correctamente la frase, debemos recordar las principales operaciones entre conjuntos que se mencionan en los incisos.
Unión: dados dos conjuntos A y B , la unión de dichos conjuntos es otro conjunto con los elementos de A y B .
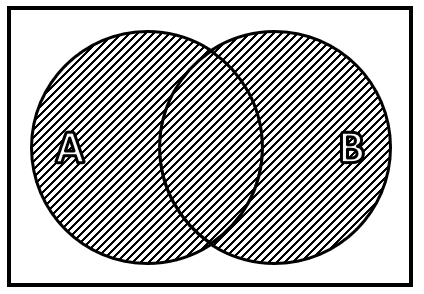
Intersección: dados dos conjuntos A y B , la intersección es otro conjunto con los elementos comunes entre A y B .
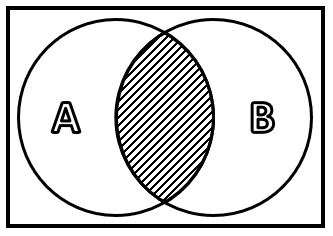
Diferencia simétrica: dados dos conjuntos A y B , la diferencia simétrica se forma con los elementos de A y B menos la intersección entre ellos.
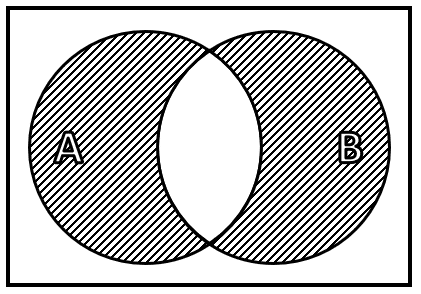
Diferencia: dados dos conjuntos A y B , la diferencia de uno con otro es otro conjunto con los elementos del minuendo que no se encuentran en el sustraendo.

Teniendo en cuenta todas estas definiciones e inspeccionando la frase incompleta, concluimos que el término que la completa es diferencia en el inciso d).
La diferencia entre dos conjuntos A y B , se forma por todos los elementos de A que no se encuentran en B .
Reactivo 46
Relacionar el diagrama de Venn con su respectiva operación de conjuntos.
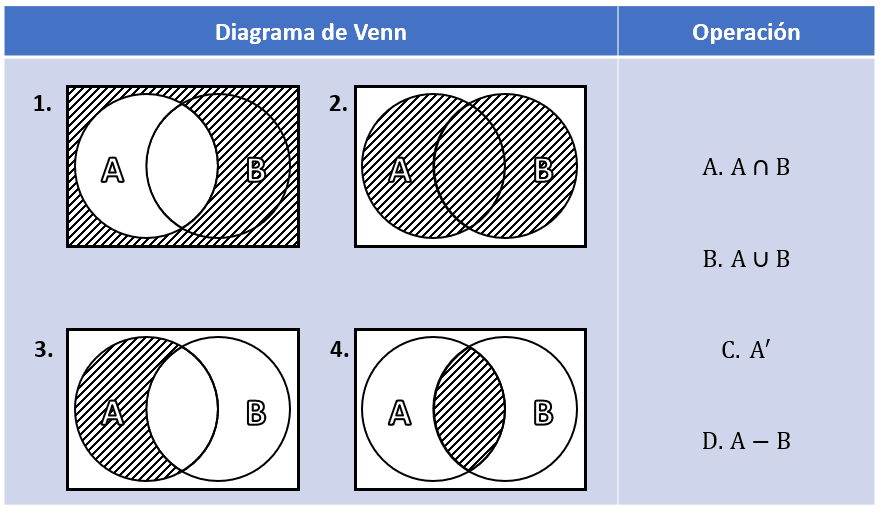
- 1C, 2B, 3D, 4A
- 1B, 2C, 3D, 4A
- 1C, 2D, 3B, 4A
- 1C, 2B, 3A, 4D
Solución:
Para encontrar la combinación correcta, debemos analizar uno a uno los diagramas de Venn que se encuentran en la columna izquierda, para determinar la operación de conjuntos que representan y luego relacionarla con uno de los incisos de la derecha.
El primer diagrama nos indica al conjunto de todos los elementos que no pertenecen a A , es decir el complemento de {A}^{c} . Examinando los incisos, indicamos: 1C.
El segundo diagrama representa a todos los elementos contenidos en A y en B a la vez, esto quiere decir, a la unión de ambos conjuntos. Para este caso: 2B.
El tercer diagrama corresponde a todos los elementos de A que no se encuentran en B . Esto corresponde a la definición de diferencia de conjuntos. Concluimos para este inciso: 3D.
Finalmente, el diagrama 4 ejemplifica la intersección entre los conjuntos A y B , por tanto: 4A. Uniendo todas las respuestas obtenemos que: 1C, 2B, 3D, 4A, comparando con las opciones, seleccionamos como respuesta correcta al inciso a).
Reactivo 47
Teniendo en cuenta los dígitos 7, 8, 9 y 0, ¿cuántos números de 2 cifras se pueden formar si se permitiera la repetición?
- 8
- 4
- 16
- 12
Solución:
Para este problema de conteo, debemos identificar si importa el orden y si se permite o no la repetición. Lo primero se responde fácilmente ya que, si pretendemos formar números, no será igual 70 que 07, por tal razón si importa el orden.
Por otro lado, el enunciado nos indica explícitamente que se permite repetir, por esta razón, concluimos que se trata de una variación con repetición cuya ecuación es:
{V}_{m}^{n}={m}^{n}
m es el total de elementos, es decir 4 y n es la cantidad de elementos que se agrupan a la vez, en este caso n=2 . Sustituimos:
{V}_{4}^{2}={4}^{2}=16
Es posible formar 16 números de 2 cifras con los dígitos 7, 8, 9 y 0.
Comparando con las opciones, concluimos que la respuesta correcta se encuentra en el inciso c).
Reactivo 48
A partir de los conjuntos A=\left\{1, 3, 5, 7\right\} y B=\left\{2, 3, 4, 5, 6\right\} , determine la operación B-A .
- \left\{2, 4, 6\right\}
- \left\{3, 5\right\}
- \left\{1, 7\right\}
- \left\{\varnothing \right\}
Solución:
Recordemos que la diferencia entre dos conjuntos B y A (como sucede en este caso) es otro conjunto con los elementos de B que no se encuentran en A . Por lo tanto, solo debemos examinar ambos conjuntos y formar otro en base a lo dicho antes.
B-A=\left\{2, 3, 4, 5, 6\right\}-\left\{1, 3, 5, 7\right\}
En este caso, prevalecen los elementos 2, 4 y 6 del conjunto B ya que estos no se encuentran en A .
B-A=\left\{2, 4, 6\right\}
Concluimos indicando como respuesta correcta la opción a).
Reactivo 49
¿Cuál es el conjunto cuyos elementos son mayores que cero, menores que 10 y múltiplos de 3?
- \left\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\right\}
- \left\{2, 4, 6, 8, 10\right\}
- \left\{3, 4, 6, 8\right\}
- \left\{3, 6, 9\right\}
Solución:
Para encontrar los elementos del conjunto, primero debemos identificar la ley o las condiciones que deben cumplir dichos elementos para pertenecer a él. Lo primero, es que se encuentren entre 0 y 10, esto se escribe matemáticamente como:
A=\left\{x|x>0\wedge x<10\right\}
Además, necesitamos que sea múltiplo de 3, esto quiere decir, que su residuo al dividir por 3 sea cero.
A=\left\{x| 0<x<10\wedge x \% 3=0\right\}
Entre el 0 y el 10 los números múltiplos de 3 son:
A=\left\{3, 6, 9\right\}
Comparando con los incisos, concluimos que la respuesta correcta es la d).
Reactivo 50
Identifique el espacio muestral que se obtiene al lanzar una moneda y luego un dado.
- \left\{S1, S2, S3, S4, S5, S6, A1, A2, A3, A4, A5, A6\right\}
- \left\{S1, S2, S3, S4, S5, S6\right\}
- \left\{A1, A2, A3, A4, A5, A6\right\}
- \left\{S123456, A123456\right\}
Solución:
Tenemos varias maneras de identificar el espacio muestral de este experimento, pero la más sencilla e intuitiva, consiste en recrear el diagrama de árbol del experimento. La primera fase consiste en lanzar una moneda, por tanto:
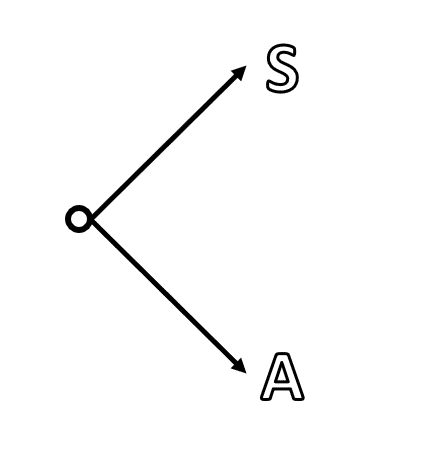
Luego, independientemente del resultado, se lanza un dado. El diagrama luego de la segunda fase queda de la siguiente manera:
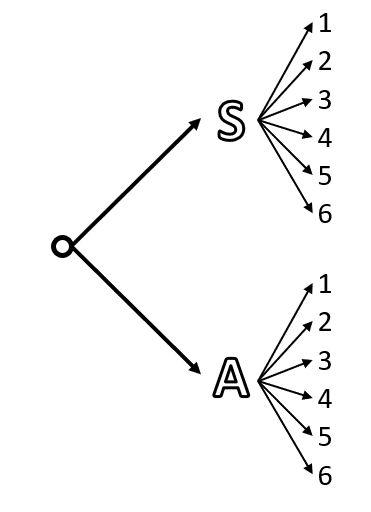
A partir del diagrama, obtenemos los siguientes eventos:
\left\{S1, S2, S3, S4, S5, S6, A1, A2, A3, A4, A5, A6\right\}
Concluimos entonces que la respuesta se encuentra en el inciso a).