Llegamos a la cuarta y última parte de la solución de los reactivos de geometría y trigonometría en la guía del IPN. En este caso, concluimos con los reactivos del 31 al 40.

¡Felicidades por llegar hasta aquí, aspirante! Recuerda que puedes continuar estudiando el resto de asignaturas con nuestras guías resuelas en materiales IPN.
Reactivo 31
Simplificar la siguiente expresión trigonométrica:
\frac{1}{2}\left[\frac{\mathrm{cos}x}{1-\mathrm{sen}x}+\frac{1-\mathrm{sen}x}{\mathrm{cos}x}\right]
- \mathrm{cot}x
- \mathrm{tan}x
- \mathrm{csc}x
- \mathrm{sec}x
Solución:
Iniciamos resolviendo la suma de fracciones.
\frac{1}{2}\left[\frac{\mathrm{cos}x}{1-\mathrm{sen}x}+\frac{1-\mathrm{sen}x}{\mathrm{cos}x}\right]=\frac{1}{2}\frac{{\mathrm{cos}}^{2}x+{\left(1-\mathrm{sen}x\right)}^{2}}{\mathrm{cos}x\left(1-\mathrm{sen}x\right)}
Desarrollamos el producto notable para el binomio al cuadrado.
\frac{1}{2}\frac{{\mathrm{cos}}^{2}x+{\left(1-\mathrm{sen}x\right)}^{2}}{\mathrm{cos}x\left(1-\mathrm{sen}x\right)}=\frac{1}{2}\frac{{\mathrm{cos}}^{2}x+1-2\mathrm{sen}x+{\mathrm{sen}}^{2}x}{\mathrm{cos}x\left(1-\mathrm{sen}x\right)}
Aplicamos la identidad pitagórica.
\frac{1}{2}\frac{1+1-2\mathrm{sen}x}{\mathrm{cos}x\left(1-\mathrm{sen}x\right)}=\frac{1}{2}\frac{2-2\mathrm{sen}x}{\mathrm{cos}x\left(1-\mathrm{sen}x\right)}=\frac{1}{2}\frac{2\left(1-\mathrm{sen}x\right)}{\mathrm{cos}x\left(1-\mathrm{sen}x\right)}
Simplificamos.
\frac{1}{2}\frac{2\left(1-\mathrm{sen}x\right)}{\mathrm{cos}x\left(1-\mathrm{sen}x\right)}=\frac{1}{2}\frac{2}{\mathrm{cos}x}=\frac{1}{\mathrm{cos}x}=\mathrm{sec}x
Finalmente:
\frac{1}{2}\left[\frac{\mathrm{cos}x}{1-\mathrm{sen}x}+\frac{1-\mathrm{sen}x}{\mathrm{cos}x}\right]=\mathrm{sec}x
Concluimos indicando como respuesta correcta al inciso d).
Reactivo 32
Determinar la función trigonométrica cuyo valor en 30° sea \frac{\sqrt{3}}{2} .
- Seno
- Coseno
- Tangente
- Cosecante
Solución:
El valor dado del ángulo es notable, por lo que deberías conocer que dicha razón trigonométrica es el coseno. Sin embargo, vamos a indicar el procedimiento para calcular razones trigonométricas sin calculadora.
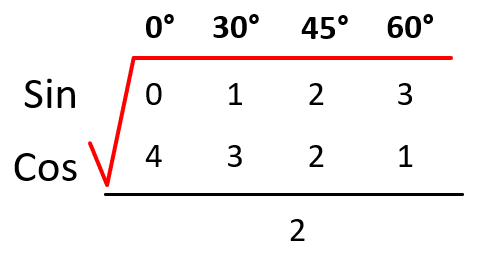
El coseno de 30° es el único que da como resultado \frac{\sqrt{3}}{2} .
La respuesta correcta es el inciso b).
Reactivo 33
Asociar la función con su valor.

- 1A, 2B, 3C, 4D
- 1B, 2C, 3D, 4A
- 1C, 2D, 3A, 4B
- 1D, 2A, 3B, 4C
Solución:
Los ángulos en los argumentos de las relaciones trigonométricas son notables, por lo que deberías conocerlos. Sin embargo, vamos a indicar un método sencillo para calcular el valor de las identidades trigonométricas para ángulos notables.

Calculamos el valor del seno de 30°.
\mathrm{sin}30°=\frac{\sqrt{1}}{2}=\frac{1}{2}
Examinando los incisos, vemos que: 1C.
Debido a que solo la opción c) inicia con 1C, concluimos que esta es la respuesta correcta.
Reactivo 34
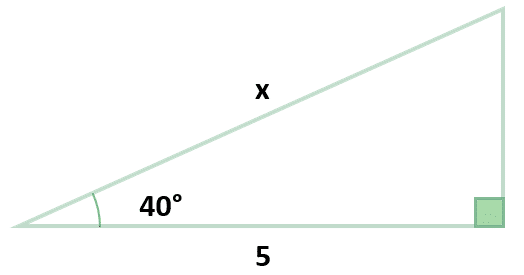
De acuerdo con la figura, determinar el valor de x .
- \frac{\mathrm{sec}\left({40}^{\circ }\right)}{5}
- 5\mathrm{sec}\left({40}^{\circ }\right)
- 5\mathrm{sen}\left({40}^{\circ }\right)
- 5\mathrm{csc}\left({40}^{\circ }\right)
Solución:
Examinando el triángulo rectángulo y los elementos que se encuentran indicados en él: uno de sus ángulos agudos y el lado adyacente a dicho ángulo. La relación trigonométrica que nos ayudará en este caso es el coseno.
\mathrm{cos}40°=\frac{5}{x}
Despejamos a la x .
x=\frac{5}{\mathrm{cos}40°}
El inverso del coseno es la secante.
x=\frac{5}{\mathrm{cos}40°}=5\mathrm{sec}40°
Concluimos que la respuesta correcta es el inciso b).
Reactivo 35
Asociar la propiedad con su igualdad.

- 1B, 2D, 3C, 4A
- 1B, 2D, 3A, 4C
- 1A, 2C, 3D, 4B
- 1A, 2C, 3B, 4D
Solución:
Vamos a ir analizando las expresiones con logaritmos que se encuentran en la columna izquierda con las igualdades de la columna derecha. Para identificar a las operaciones con las igualdades, es necesario que conozcas las propiedades de los logaritmos.
Primera propiedad.
\mathrm{log}\left(ab\right)
Esta es la propiedad del logaritmo del producto. Es igual a la suma de los logaritmos de los números.
\mathrm{log}\left(ab\right)=\mathrm{log}\left(a\right)+\mathrm{log}\left(b\right)
Tenemos que: 1B. Aunque la igualdad se realiza con logaritmos naturales, la propiedad es aplicable para logaritmos con cualquier base.
Segunda propiedad.
\mathrm{log}\left({b}^{a}\right)
Es la propiedad del logaritmo de una potencia. Es igual al producto del exponente por el logaritmo de la base.
\mathrm{log}\left({b}^{a}\right)=a\mathrm{log}\left(b\right)
Tenemos que: 2D.
Tercera propiedad.
\mathrm{log}\left(\frac{a}{b}\right)
Es la propiedad del logaritmo de un cociente. Es igual a la diferencia de los logaritmos del numerador y denominador.
\mathrm{log}\left(\frac{a}{b}\right)=\mathrm{log}\left(a\right)-\mathrm{log}\left(b\right)
Tenemos que: 3A.
Con estas respuestas parciales: 1B, 2D, 3A, … podemos concluir que la respuesta correcta es el inciso b).
Reactivo 36
Determinar \mathrm{tan}\left(\alpha \right) en un triángulo rectángulo, si se sabe que \mathrm{cos}\left(\alpha \right)=\frac{3}{5} .
- 4/3
- 3/2
- 5
- 7
Solución:
A partir del coseno del ángulo, sabemos cuánto mide el cateto adyacente y la hipotenusa del triángulo.
\mathrm{cos}\left(\alpha \right)=\frac{3}{5}=\frac{CA}{H}
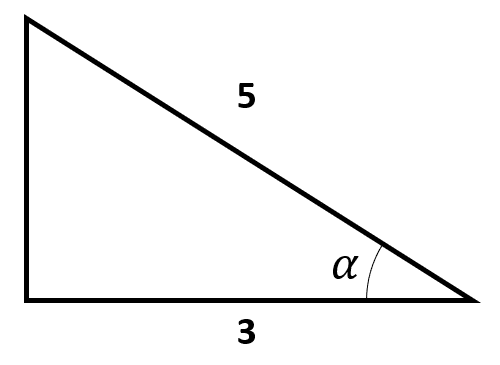
Por otra parte, la tangente del ángulo se calcula como el cociente entre el cateto opuesto y el cateto adyacente. El cateto opuesto se puede calcular aplicando el teorema de Pitágoras.
{5}^{2}={3}^{2}+C{O}^{2}\to CO=\sqrt{25-9}=4
Finalmente:
\mathrm{tan}\alpha =\frac{4}{3}
Seleccionamos como respuesta correcta al inciso a).
Reactivo 37
Relacionar la expresión con el tipo de función exponencial que le corresponde.

- 1D, 2C, 3B, 4A
- 1D, 2B, 3A, 4C
- 1C, 2A, 3D, 4B
- 1C, 2A, 3B, 4D
Solución:
Debemos analizar cada una de las funciones que se encuentran en la columna izquierda para relacionarlas de forma correcta con las definiciones en la columna derecha.
Primera función:
f\left(x\right)={1}^{x}
Esta no es una función exponencial, aunque lo parezca debido a que la base es 1. No importa el exponente que se sustituya en la función, el resultado será siempre 1. Tenemos: 1C.
Segunda función:
g\left(x\right)={5}^{3x}
Esta es una función exponencial. Tenemos para este caso: 2A. Descartamos los incisos a y b, pero debemos continuar con la siguiente función para decidir entre c y d.
Tercera función:
s\left(x\right)={e}^{x}
Esta es una función exponencial con base igual al número de Euler. A esta función en particular se le conoce como exponencial natural. Finalmente: 1C, 2A, 3D, … esta información es suficiente para concluir que la respuesta correcta es el inciso c).
Reactivo 38
Relacionar la expresión con el tipo de función logarítmica que le corresponde.

- 1B, 2D, 3A, 4C
- 1D, 2A, 3C, 4B
- 1D, 2B, 3A, 4C
- 1B, 2D, 3C, 4A
Solución:
Comenzamos con la expresión del inciso 1, tenemos un producto de potencias de igual base. Siguiendo la propiedad que lleva el mismo nombre, se mantiene la base y se suman los exponentes.
{a}^{n}{a}^{m}={a}^{n+m}
Tenemos: 1B, descartamos a las opciones a y d.
Vamos con la segunda expresión:
\frac{{a}^{n}}{{a}^{m}}
Es un cociente de potencias de igual base. Se mantiene la base, pero se restan los exponentes.
\frac{{a}^{n}}{{a}^{m}}={a}^{n-m}
Para esta segunda expresión tenemos: 2D.
La tercera expresión es:
\frac{1}{{a}^{n}}
Aplicando la propiedad del exponente negativo obtenemos:
\frac{1}{{a}^{n}}={a}^{-n}
Tenemos: 3A. Uniendo las respuestas parciales: 1B, 2D, 3A, … concluimos que la opción a) resuelve correctamente al ejercicio.
Reactivo 39
Si {\mathrm{l}\mathrm{o}\mathrm{g}}_{2\sqrt[3]{2}}y=3 , entonces y=
- 4\sqrt{2}
- 16
- 4
- 2
Solución:
Debemos recordar la definición de logaritmo.
{b}^{x}=n\to {\mathrm{log}}_{b}n=x
Aplicada a este caso:
b=2\sqrt[3]{2}, n=y, x=3
{\left(2\sqrt[3]{2}\right)}^{3}=y
{2}^{3}\cdot 2=y\to y=16
La respuesta correcta es el inciso b).
Reactivo 40
¿Cuál es el desarrollo de la siguiente expresión logarítmica?
\mathrm{l}\mathrm{n}\left(\frac{(3-x{)}^{2}(4-3x)}{{2}^{3}(x+2{)}^{3}}\right)
- 2\mathrm{ln}\left(3-x\right)+\mathrm{ln}\left(4-3x\right)-3\mathrm{ln}\left(x+2\right)
- 2\mathrm{ln}\left(3-x\right)+\mathrm{ln}\left(4-3x\right)-3\mathrm{ln}\left(2x+4\right)
- 2\mathrm{ln}\left(3-x\right)+2\mathrm{ln}\left(4-3x\right)-6\mathrm{ln}\left(x+2\right)
- 2\mathrm{ln}\left(3-x\right)-\mathrm{ln}\left(4-3x\right)-6\mathrm{ln}\left(x+2\right)
Solución:
Para desarrollar la expresión, debemos aplicar las propiedades del logaritmo del producto y del cociente de forma conveniente. Iniciamos con la propiedad del logaritmo del cociente.
\mathrm{ln}\left(\frac{(3-x{)}^{2}(4-3x)}{{2}^{3}(x+2{)}^{3}}\right)=\mathrm{ln}\left((3-x{)}^{2}(4-3x)\right)-\mathrm{ln}\left({2}^{3}(x+2{)}^{3}\right)
Ahora, aplicamos la propiedad del logaritmo del producto.
\mathrm{ln}\left((3-x{)}^{2}(4-3x)\right)-\mathrm{ln}\left({2}^{3}(x+2{)}^{3}\right)=\mathrm{ln}\left((3-x{)}^{2}\right)+\mathrm{ln}\left(4-3x\right)-\mathrm{ln}\left({2}^{3}\right)-\mathrm{ln}\left((x+2{)}^{3}\right)
Finalmente, aplicamos la propiedad del logaritmo de una potencia, para bajar el exponente del argumento.
=2\mathrm{ln}\left(3-x\right)+\mathrm{ln}\left(4-3x\right)-3\mathrm{ln}\left(2\right)-3\mathrm{ln}\left(x+2\right)
Extraemos el -3 factor común de los últimos dos términos. Aplicamos de nuevo la propiedad del logaritmo del producto en sentido inverso.
2\mathrm{ln}\left(3-x\right)+\mathrm{ln}\left(4-3x\right)-3\mathrm{ln}\left(2\left(x+2\right)\right)=2\mathrm{ln}\left(3-x\right)+\mathrm{ln}\left(4-3x\right)-3\mathrm{ln}\left(2x+4\right)
Finalmente:
\mathrm{ln}\left(\frac{(3-x{)}^{2}(4-3x)}{{2}^{3}(x+2{)}^{3}}\right)=2\mathrm{ln}\left(3-x\right)+\mathrm{ln}\left(4-3x\right)-3\mathrm{ln}\left(2x+4\right)
Comparando con las opciones, concluimos que la respuesta correcta es b).

