¡Continuamos, aspirante! Esta vez resolvemos tercera parte de la guía de probabilidad y estadística del IPN. En este caso, vamos a desarrollar paso a paso los reactivos desde el 21 hasta el 30.

¿Te parece difícil algún reactivo? ¡No te preocupes! En cada solución te mencionamos algunos de los hacks que explicamos en el curso.
Reactivo 21
Se entrevistó a 80 personas en una plaza comercial para saber si preferían comer pizza o ensalada. El resultado indicó que a 13 no les gusta ni la pizza ni la ensalada y a 45 les gusta solo la pizza.
Si 5 personas señalaron que les gusta comer ambas cosas, ¿cuántos prefieren comer solo ensalada?
- 11
- 15
- 17
- 20
Solución:
En el enunciado se describen cuatro subconjuntos de personas: los que prefieren pizza, los que prefieren ensalada, los que prefieren ambas y los que no prefieren ninguna de las dos. Por ende, el total de elementos del universo, es igual a la suma de las personas que conforman los 4 conjuntos.
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}={C}_{1}+{C}_{2}+{C}_{3}+{C}_{4}
El conjunto {C}_{2} corresponde con aquellos que solo prefieren ensalada. Despejamos esta variable y la evaluamos.
{C}_{2}=\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}-{C}_{1}-{C}_{3}-{C}_{4}=80-45-5-13
{C}_{2}=17
De las 17 personas en todo el estudio, solo prefieren comer ensalada.
La respuesta correcta es el inciso c).
Reactivo 22
Una persona sostiene en cada mano una moneda, pero una de ellas tiene doble cara. Si le pide a alguien que elija una moneda para lanzarla al aire, ¿cuál es la probabilidad de que salga cruz?
- 0
- 25
- 5
- 75
Solución:
En el experimento en general, hay 3 caras (por la moneda que tiene 2 caras) y una cruz. Por lo tanto, la probabilidad de que salga cruz se calcula como:
P\left(\mathrm{c}\mathrm{r}\mathrm{u}\mathrm{z}\right)=\frac{1}{4}=0.25
Hay un 25% de que salga cruz.
Indicamos como respuesta correcta al inciso b).
Reactivo 23
Si se sabe que P\left(B\right)=1/2\text{ y }P(A\cap B)=\frac{1}{4} , determinar P\left(A\right) .
- 1/2
- 1/3
- 1/4
- 1/5
Solución:
La probabilidad de la intersección de sucesos independientes se calcula como:
P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)
Aunque no se indica explícitamente que los sucesos son independientes, en el enunciado no se indica el valor de P\left(A\cup B\right) . Por esta razón, podemos concluir que los sucesos son independientes.
Sustituimos y despejamos P\left(A\right) .
\frac{1}{4}=P\left(A\right)\cdot \frac{1}{2}\to P\left(A\right)=\frac{1}{2}
La respuesta correcta es el inciso a).
Reactivo 24
Determinar la probabilidad del evento \left(A\cap B\right) dado que A y B son eventos independientes y P\left(A\right)=\frac{1}{5}\text{ y }P\left(B\right)=\frac{1}{3} .
- 1/15
- 1/8
- 1/2
- 3/4
Solución:
La probabilidad de la intersección de sucesos independientes se calcula como:
P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)
Sustituimos.
P\left(A\cap B\right)=\left(\frac{1}{5}\right)\left(\frac{1}{3}\right)=\frac{1}{15}
La respuesta correcta es el inciso a).
Reactivo 25
Una urna contiene 5 bolas rojas y 4 blancas. Si se extrae una de un color, se reemplaza por 3 del color opuesto y, después, se extrae una segunda bola, ¿cuál es la probabilidad de que las dos bolas sean del mismo color?
- \frac{24}{99}
- \frac{20}{99}
- \frac{35}{99}
- \frac{32}{99}
Solución:
Nota: este reactivo tenía un error en los incisos. Lo hemos modificado para que muestre la respuesta correcta.
Debido a que debemos calcular la probabilidad de extraer el mismo color, con las condiciones impuestas en el enunciado, debemos calcular la probabilidad de extraer rojo dos veces y luego blanco dos veces. La probabilidad total será la suma de las anteriores.
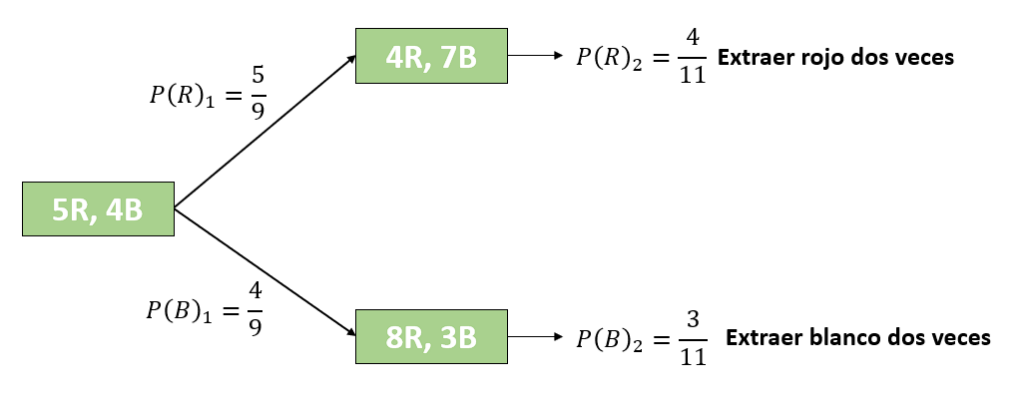
Empleamos la probabilidad total.
P\left(\mathrm{M}\mathrm{C}\right)=P\left(R\right)\cdot P\left(\frac{R}{R}\right)+P\left(B\right)\cdot P\left(\frac{B}{B}\right)=\left(\frac{5}{9}\right)\left(\frac{4}{11}\right)+\left(\frac{4}{9}\right)\left(\frac{3}{11}\right)
P\left(\mathrm{M}\mathrm{C}\right)=\frac{20}{99}+\frac{12}{99}=\frac{32}{99}
La probabilidad de sacar el mismo color dos veces seguidas es \frac{32}{99} .
La respuesta correcta es el inciso d).
Reactivo 26
En una fábrica se producen cajas de metal en tres máquinas (M1, M2 y M3). El 20% se produce en M1, el 30% en M2 y el resto en M3. Sin embargo, se sabe que en cada lote hay un porcentaje de cajas defectuosas: el 1% viene de M1, el 2% de M2 y el 7% de M3.
Si elegimos una caja entre toda la producción, ¿cuál es la probabilidad de que esta sea defectuosa?
- 4.3%
- 4.4%
- 4.5%
- 4.6%
Solución:
Primero debemos calcular la probabilidad de que salga una caja defectuosa de cada máquina y luego sumamos los resultados para obtener la probabilidad total de obtener una caja defectuosa de la producción total.
El siguiente diagrama de árbol nos permitirá visualizar la situación.
Ahora, colocamos el porcentaje en cada rama del diagrama.
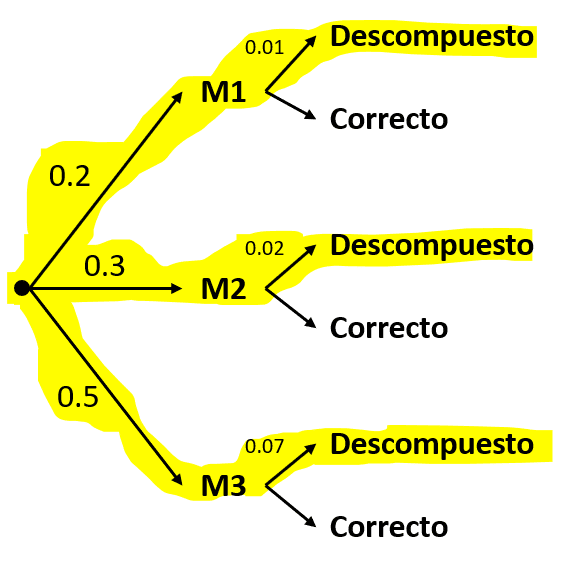
Finalmente, la probabilidad que sea defectuosa es:
P\left(D\right)=\left(0.2\right)\left(0.01\right)+\left(0.3\right)\left(0.02\right)+\left(0.5\right)\left(0.07\right)
P\left(D\right)=0.002+0.006+0.035=0.043
La probabilidad de que la caja sea defectuosa es del 4.3%.
Concluimos que la respuesta correcta es el inciso a).
Reactivo 27
Considerando la siguiente tabla de distribución de frecuencias, determinar el valor de la media

- 2
- 1
- 2
- 3
Solución:
Nota: este reactivo tenía un error en los incisos. Ha sido modificado para que muestre la respuesta correcta.
La media aritmética se calcula como:
\stackrel{-}{x}=\frac{1+2+3+3+1}{5}
Resolvemos.
\stackrel{-}{x}=2
La respuesta correcta es el inciso a). Acotamos que, originalmente, en este reactivo había un error tanto en los incisos como en la respuesta correcta.
Reactivo 28
Se aplicó una encuesta a 40 personas para saber cuántas mascotas tienen. Con base en los datos obtenidos, determinar la mediana.
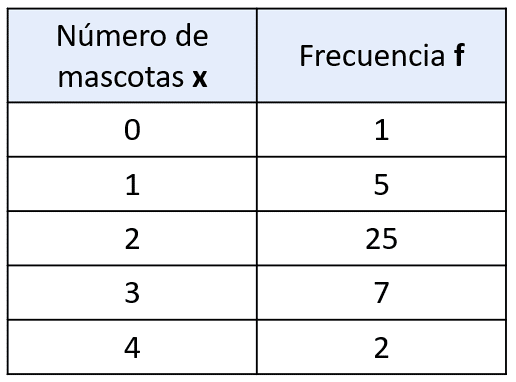
- 2
- 5
- 7
- 25
Solución:
La mediana es el parámetro estadístico que divide en dos partes iguales a todos los datos. Cuando el conjunto no está agrupado, como en este caso, la mediana se calcula:
- Si el número de datos es par, se toma el promedio de los datos centrales.
- Si el número de datos es impar, se toma al valor central.
En la tabla de datos hay 5 filas, por lo tanto, la mediana es tener 2 mascotas. La respuesta correcta es el inciso a).
Reactivo 29
¿Qué relación se tiene entre la media armónica, geométrica y aritmética, (H,G\text{ у }\stackrel{-}{X}) ?
- H\le \stackrel{-}{X}\le G
- G\le \stackrel{-}{X}\le H
- H\le G\le \stackrel{-}{X}
- \stackrel{-}{X}\le H\le G
Solución:
El enunciado hace referencia a la desigualdad de las medias. Recordemos cómo se calcula cada una de las medias.
Media aritmética.
{m}_{a}=\frac{\sum {x}_{i}}{n}
Media geométrica.
{m}_{g}=\sqrt[n]{\prod {x}_{i}}
Media armónica.
{m}_{ar}=\frac{1}{{m}_{a}}=\frac{n}{\sum {x}_{i}}
La demostración de esta desigualdad es bastante extensa. Es necesario que la conozcas de antemano. La desigualdad de las medias establece que:
{m}_{ar}\le {m}_{g}\le {m}_{a}
Adoptando la nomenclatura del enunciado:
H\le G\le \stackrel{-}{X}
La respuesta correcta es el inciso c).
La siguiente tabla de frecuencias reúne información sobre el peso en Kg de 90 empleados de una empresa. Con base en esto, responder las preguntas 30 a 32.
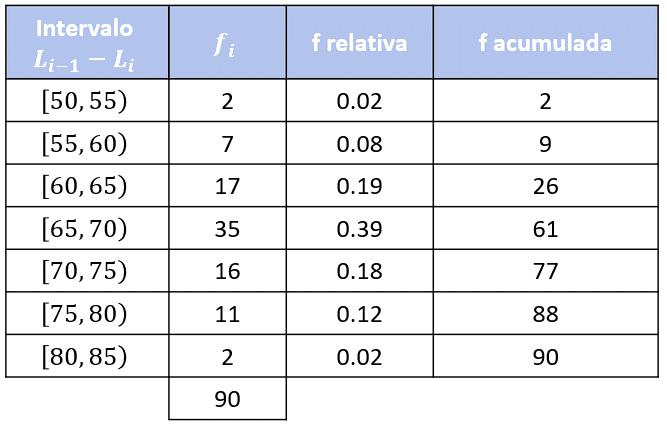
Reactivo 30
¿Cuáles el porcentaje de personas que pesan menos de 60 Kg?
- 2%
- 8%
- 10%
- 12%
Solución:
Debemos sumar las frecuencias de las clases que se encuentran por debajo de los 60 kilogramos. Examinando la tabla, dichas clases son: \left[50, 55\right) y \left[55, 60\right) ; cuyas frecuencias absolutas son 2 y 7 respectivamente.
El total de personas con al menos 60 kg de pesos es 9. Calculamos el porcentaje como:
{\%}_{\le 90}=\frac{9}{90}\cdot 100\%=10\%
El 10% de las personas que participaron en el estudio pesan al menos 60 kilogramos.
La respuesta correcta es el inciso c).


