Guía IPN 2023 Cálculo Integral Parte 4 del 31 al 40

¡Llegamos a la última parte! En este tutorial vamos a resolver la cuarta parte de la guía de cálculo integral IPN, correspondiente a los reactivos desde el 31 al 40.

Estudia el resto de asignaturas que hemos preparado en la zona de materiales IPN. No olvides incorporar exámenes simulacro en tus jornadas de estudio, monitorea tus tiempos y perfecciónalos antes de la prueba de ingreso.

Reactivo 31

Resolver la integral \int \frac{dx}{x\left(x-\frac{5}{3}\right)} .

1. \frac{3}{5}\mathrm{ln}\left|\frac{x}{3x-5}\right|+C
2. \frac{3}{5}\mathrm{ln}\left|\frac{x}{5x-3}\right|+C
3. \frac{3}{5}\mathrm{ln}\left|\frac{3x-5}{x}\right|+C
4. \frac{3}{5}\mathrm{ln}\left|\frac{5x-3}{x}\right|+C

Solución:

Para resolver la integral, debemos descomponer en fracciones parciales al integrando.

\frac{1}{x\left(x-\frac{5}{3}\right)}=\frac{A}{x}+\frac{B}{x-\frac{5}{3}}

Pasamos a multiplicar el denominador de la fracción de la izquierda.

1=A\left(x-\frac{5}{3}\right)+Bx

Desarrollamos.

1=Ax-\frac{5}{3}A+Bx\to \left(A+B\right)x-\frac{5}{3}A=1

Igualamos los coeficientes para calcular el valor de los coeficientes.

\left\{\begin{array}{c}A+B=0\\ -\frac{5}{3}A=1\end{array}\right.

Despejamos el valor de A , con la segunda ecuación.

-\frac{5}{3}A=1\to A=-\frac{3}{5}

Ahora, despejamos a B .

A+B=0\to B=-A\to B=\frac{3}{5}

La descomposición en fracciones parciales es:

\frac{1}{x\left(x-\frac{5}{3}\right)}=-\frac{3}{5x}+\frac{3}{5\left(x-\frac{5}{3}\right)}

Sustituyendo en la integral:

\int \frac{dx}{x\left(x-\frac{5}{3}\right)}=-\frac{3}{5}\int \frac{1}{x}dx+\frac{3}{5}\int \frac{1}{x-\frac{5}{3}}dx=-\frac{3}{5}\int \frac{1}{x}dx+\frac{3}{5}\int \frac{3}{3x-5}dx

La integral nos queda:

-\frac{3}{5}\int \frac{1}{x}dx+\frac{3}{5}\int \frac{3}{3x-5}dx

Para ambas integrales, aplicamos la fórmula de la integral del inverso de x . En la integral del segundo término, ya tenemos el diferencial de 3x-5 es como 3dx .

-\frac{3}{5}\int \frac{1}{x}dx+\frac{3}{5}\int \frac{3dx}{3x-5}=-\frac{3}{5}\mathrm{ln}\left|x\right|+\frac{3}{5}\mathrm{ln}\left|3x-5\right|+C

Aplicamos la propiedad del logaritmo del cociente.

-\frac{3}{5}\mathrm{ln}\left|x\right|+\frac{3}{5}\mathrm{ln}\left|3x-5\right|+C=\frac{3}{5}\mathrm{ln}\left|\frac{3x-5}{x}\right|+C

Finalmente:

\int \frac{dx}{x\left(x-\frac{5}{3}\right)}=\frac{3}{5}\mathrm{ln}\left|\frac{3x-5}{x}\right|+C

La respuesta correcta es el inciso c).

Sigue practicando la parte de cálculo integral:

• Parte 1: Ejercicios del 1 al 10
• Parte 2: Ejercicios del 11 al 20
• Parte 3: Ejercicios del 21 al 30

Reactivo 32

Calcular la integral por fracciones parciales.

\int \frac{{x}^{2}-6x-11}{{x}^{3}+3{x}^{2}-x-3}dx

1. \mathrm{ln}\left|\frac{(x+1)(x+3{)}^{2}}{(x-1{)}^{2}}\right|+c
2. \mathrm{ln}\left|\frac{\left(x+1\right)\left(x+3\right)}{x-1}\right|+c
3. \mathrm{ln}\left|\frac{(x+1{)}^{2}(x+3)}{x-1}\right|+c
4. \mathrm{ln}\left|\frac{(x+1)(x+3{)}^{2}}{\left(x-1\right)}\right|+c

Solución:

Para aplicar fracciones parciales, debemos factorizar el denominador del integrando. Debido a que es un polinomio de tercer grado, es necesario utilizar Ruffini o la división sintética. En este caso, utilizaremos la regla de Ruffini.

Copiamos los coeficientes del polinomio.

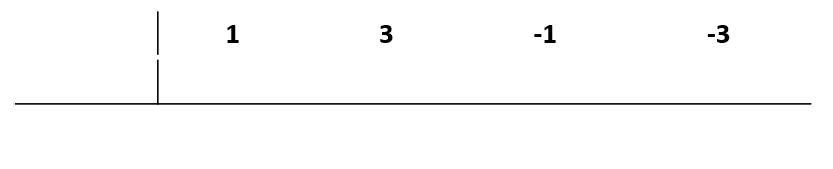
No vamos a describir el procedimiento, pero sí dejaremos el paso a paso.

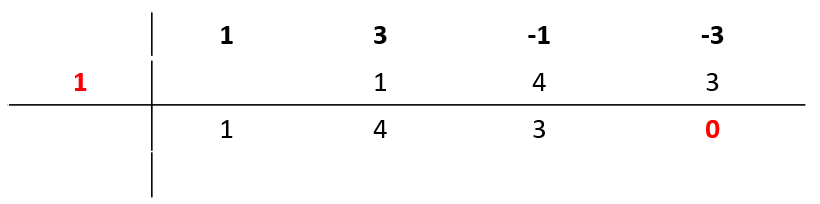
La primera raíz es x=1 .

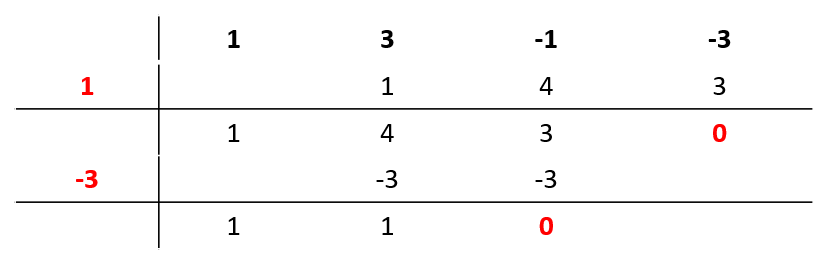
La segunda raíz es x=-3 .

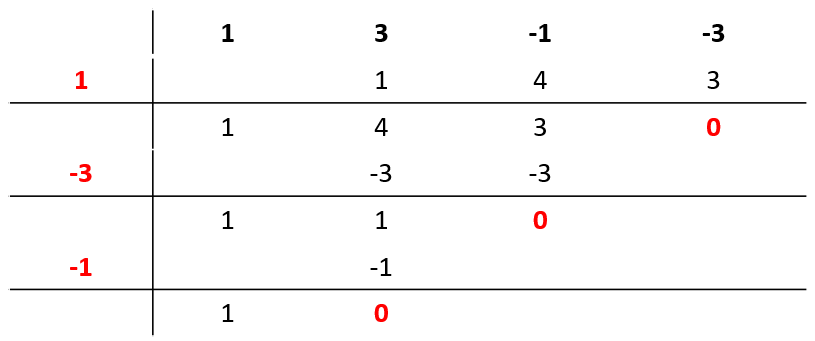
La tercera y última raíz es x=-3 . Finalmente:

{x}^{3}+3{x}^{2}-x-3=\left(x+3\right)\left(x-1\right)\left(x+1\right)

Sustituimos en la integral.

\int \frac{{x}^{2}-6x-11}{{x}^{3}+3{x}^{2}-x-3}dx=\int \frac{{x}^{2}-6x-11}{\left(x+3\right)\left(x-1\right)\left(x+1\right)}dx

Descomponemos en fracciones parciales.

\frac{{x}^{2}-6x-11}{\left(x+3\right)\left(x-1\right)\left(x+1\right)}=\frac{A}{x+3}+\frac{B}{x+1}+\frac{C}{x-1}

{x}^{2}-6x-11=A\left(x-1\right)\left(x+1\right)+B\left(x+3\right)\left(x-1\right)+C\left(x+3\right)\left(x+1\right)

Desarrollamos y agrupamos.

{x}^{2}-6x-11=A\left({x}^{2}-1\right)+B\left({x}^{2}+2x-3\right)+C\left({x}^{2}+4x+3\right)

{x}^{2}-6x-11={x}^{2}\left(A+B+C\right)+x\left(2B+4C\right)-A-3B+3C

Igualamos los coeficientes.

\left\{\begin{array}{c}A+B+C=1\\ 2B+4C=-6\\ -A-3B+3C=-11\end{array}\right.

Tenemos un sistema de 3 ecuaciones con 3 incógnitas. Vamos a saltar este paso, pero puedes utilizar el método de solución que prefieras.

A=2, B=1, C=-2

Sustituimos en la descomposición.

\frac{{x}^{2}-6x-11}{\left(x+3\right)\left(x-1\right)\left(x+1\right)}=\frac{2}{x+3}+\frac{1}{x+1}-\frac{2}{x-1}

Sustituimos en la integral y resolvemos.

\int \frac{{x}^{2}-6x-11}{{x}^{3}+3{x}^{2}-x-3}dx=\int \frac{2}{x+3}dx+\int \frac{1}{x+1}dx-\int \frac{2}{x-1}dx

En las tres integrales aplicamos la fórmula para la integral del inverso de x .

\int \frac{2}{x+3}dx+\int \frac{1}{x+1}dx-\int \frac{2}{x-1}dx=2\mathrm{ln}\left|x+3\right|+\mathrm{ln}\left|x+1\right|-2\mathrm{ln}\left|x-1\right|+C

Ahora, aplicamos las propiedades del logaritmo de una potencia, de un producto y de un cociente para reacomodar el resultado.

2\mathrm{ln}\left|x+3\right|+\mathrm{ln}\left|x+1\right|-2\mathrm{ln}\left|x-1\right|+C=\mathrm{ln}{\left|x+3\right|}^{2}+\mathrm{ln}\left|x+1\right|-\mathrm{ln}{\left|x-1\right|}^{2}+C

\mathrm{ln}{\left|x+3\right|}^{2}+\mathrm{ln}\left|x+1\right|-\mathrm{ln}{\left|x-1\right|}^{2}+C=\mathrm{ln}\left|{\left(x+3\right)}^{2}\left(x+1\right)\right|-\mathrm{ln}{\left|x-1\right|}^{2}+C

\mathrm{ln}\left|{\left(x+3\right)}^{2}\left(x+1\right)\right|-\mathrm{ln}{\left|x-1\right|}^{2}+C=\mathrm{ln}\left|\frac{{\left(x+3\right)}^{2}\left(x+1\right)}{{\left(x-1\right)}^{2}}\right|+C

Finalmente:

\int \frac{{x}^{2}-6x-11}{{x}^{3}+3{x}^{2}-x-3}dx=\mathrm{ln}\left|\frac{{\left(x+3\right)}^{2}\left(x+1\right)}{{\left(x-1\right)}^{2}}\right|+C

Concluimos indicando como respuesta correcta al inciso a).

Reactivo 33

Elegir la integral que es equivalente a \int \frac{3xdx}{(x-7{)}^{3}} usando fracciones parciales.

1. \frac{A}{x-7}+\frac{B}{(x-7{)}^{2}}+\frac{Cx}{(x-7{)}^{3}}
2. \frac{A}{x-7}+\frac{Bx}{(x-7{)}^{2}}+\frac{C}{(x-7{)}^{3}}
3. \frac{Ax}{x-7}+\frac{B}{(x-7{)}^{2}}+\frac{Cx}{(x-7{)}^{3}}
4. \frac{A}{x-7}+\frac{C}{(x-7{)}^{2}}+\frac{B}{(x-7{)}^{3}}

Solución:

El integrando tiene una raíz lineal repetida tres veces. La descomposición en fracciones sería:

\frac{3x}{{\left(x-7\right)}^{3}}=\frac{A}{x-7}+\frac{B}{{\left(x-7\right)}^{2}}+\frac{C}{{\left(x-7\right)}^{3}}

La respuesta correcta es el inciso d).

Reactivo 34

Indicar el sistema de ecuaciones que se plantea al resolver la integral.

\int \frac{\left(5x+30\right)dx}{{x}^{2}-3x+2}

1. A+B=5,-B-2A=30
2. A+B=5,B+2A=30
3. A-B=5,-B-2A=20
4. A-B=5,B+2A=20

Solución:

Primero factorizamos el trinomio del denominador. Buscamos dos números que sumados sean -3 y multiplicados +2, estos son: -1 y -2.

{x}^{2}-3x+2=\left(x-1\right)\left(x-2\right)

Sustituimos en el integrando.

\int \frac{\left(5x+30\right)dx}{{x}^{2}-3x+2}=\int \frac{\left(5x+30\right)dx}{\left(x-1\right)\left(x-2\right)}

Aplicando descomposición en fracciones parciales:

\frac{5x+30}{\left(x-1\right)\left(x-2\right)}=\frac{A}{x-1}+\frac{B}{x-2}

Pasamos a multiplicar los factores del denominador de la fracción del primer miembro.

5x+30=A\left(x-2\right)+B\left(x-1\right)

Desarrollamos y agrupamos.

5x+30=Ax-2A+Bx-B\to 5x+30=\left(A-B\right)x-2A-B

Igualamos los coeficientes.

\left\{\begin{array}{c}A+B=5\\ -2A-B=30\end{array}\right.

Este es el sistema de ecuaciones que permite calcular el valor de los coeficientes.

Comparando con los incisos, concluimos que la respuesta correcta es el inciso a).

Reactivo 35

El teorema fundamental del cálculo afirma que la integral definida {\int }_{a}^{b} f\left(x\right)dx es:

1. F\left(a\right)-F\left(b\right)
2. f\left(b\right)-f\left(a\right)
3. F\left(b\right)-F\left(a\right)
4. f\left(a\right)-f\left(b\right)

Solución:

En cálculo hay dos teoremas fundamentales y el segundo es el que nos habla de las integrales definidas como herramientas para determinar el área bajo una curva. El segundo teorema fundamental del cálculo establece que:

Dada una función f continua en un intérvalo \left[a, b\right] y F es una antiderivada de f , entonces:

{\int }_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)

La respuesta correcta es el inciso a).

Reactivo 36

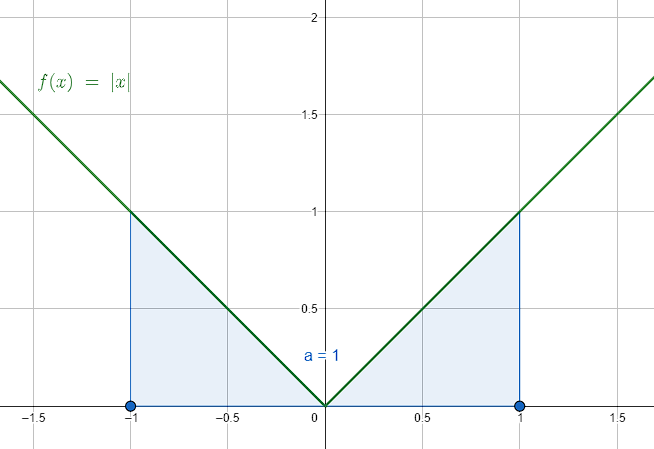
Resolver la integral {\int }_{-1}^{1}\left|x\right|dx  .

1. 0
2. ½
3. 1
4. 2

Solución:

Para calcular el área bajo la función valor absoluto, debemos reescribirla como una función a trozos.

\left|x\right|=\left\{\begin{array}{c}x si x\ge 0\\ -x si x<0\end{array}\right.

Teniendo en cuenta esto, utilizamos a -x para integrar desde -1 hasta 0 y x para el intervalo de 0 a 1. La integral definida quedaría reescrita como:

{\int }_{-1}^{1}\left|x\right|dx ={\int }_{-1}^{0}-xdx+{\int }_{0}^{1}xdx

Ambas integrales son inmediatas.

{\int }_{-1}^{0}-xdx+{\int }_{0}^{1}xdx=\begin{array}{c} \\ -\frac{{x}^{2}}{2}\\  \end{array}⟧\begin{array}{c}0\\  \\ -1\end{array}+\begin{array}{c} \\ \frac{{x}^{2}}{2}\\  \end{array}⟧\begin{array}{c}1\\  \\ 0\end{array}=-\left(\frac{0}{2}-\frac{1}{2}\right)+\left(\frac{1}{2}-0\right)=\frac{1}{2}-\frac{1}{2}=1 {u}^{2}

Finalmente:

{\int }_{-1}^{1}\left|x\right|dx =1 {u}^{2}

La respuesta correcta es el inciso c).

Reactivo 37

Resolver la siguiente integral:

{\int }_{1}^{2} \sqrt[4]{{x}^{3}}dx

1. \frac{4}{7}\left(2\sqrt[4]{8}+1\right)
2. \frac{4}{7}\left(2\sqrt[4]{8}-1\right)
3. \frac{4}{7}\left(\sqrt[4]{8}+1\right)
4. \frac{4}{7}\left(\sqrt[4]{8}-1\right)

Solución:

Expresamos al integrando en forma de potencia y resolvemos.

{\int }_{1}^{2} \sqrt[4]{{x}^{3}}dx={\int }_{1}^{2} {x}^{\frac{3}{4}}dx=\begin{array}{c} \\ \frac{{x}^{\frac{3}{4}+1}}{\frac{3}{4}+1}\\  \end{array}⟧\begin{array}{c}2\\  \\ 1\end{array}=\frac{4}{7}\begin{array}{c} \\ {x}^{\frac{7}{4}}\\  \end{array}⟧\begin{array}{c}2\\  \\ 1\end{array}=\frac{4}{7}{\left(2\right)}^{\frac{7}{4}}-\frac{4}{7}{\left(1\right)}^{\frac{7}{4}}

\frac{4}{7}{\left(2\right)}^{\frac{7}{4}}-\frac{4}{7}{\left(1\right)}^{\frac{7}{4}}=\frac{4}{7}{\left(2\right)}^{\frac{7}{4}}-\frac{4}{7}=\frac{4}{7}\left[\sqrt[4]{{2}^{7}}-1\right]=\frac{4}{7}\left[\sqrt[4]{{2}^{4}\cdot {2}^{3}}-1\right]

\frac{4}{7}\left[\sqrt[4]{{2}^{4}\cdot {2}^{3}}-1\right]=\frac{4}{7}\left[2\sqrt[4]{8}-1\right]\approx 1.3506 {u}^{2}

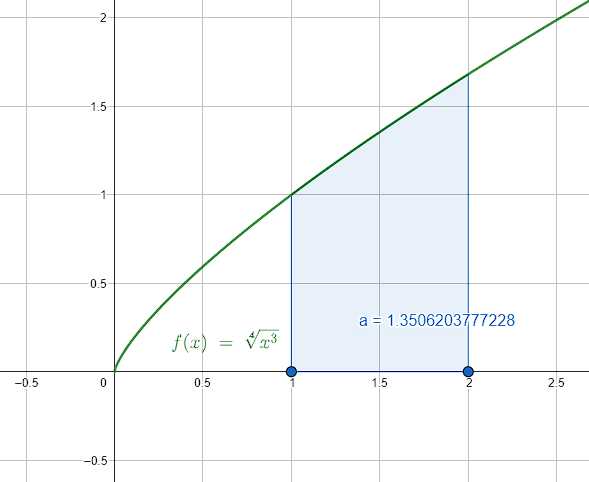
La respuesta correcta es el inciso b).

Reactivo 38

Determinar el área bajo la curva en el intervalo \left[0, 1\right] de la siguiente función:

f\left(x\right)=\sqrt{x}+1

1. \frac{5}{3}
2. \frac{5}{4}
3. 1
4. \frac{5}{6}

Solución:

La integral definida de la función quedaría:

{\int }_{0}^{1}\left(\sqrt{x}+1\right)dx

Resolvemos.

{\int }_{0}^{1}\left(\sqrt{x}+1\right)dx={\int }_{0}^{1}\sqrt{x}dx+{\int }_{0}^{1}dx={\int }_{0}^{1}{x}^{1/2}dx+{\int }_{0}^{1}dx=\begin{array}{c} \\ \frac{2}{3}{x}^{\frac{3}{2}}\\  \end{array}⟧\begin{array}{c}1\\  \\ 0\end{array}+\begin{array}{c} \\ x\\  \end{array}⟧\begin{array}{c}1\\  \\ 0\end{array}

Aplicando el teorema fundamental del cálculo.

\begin{array}{c} \\ \frac{2}{3}{x}^{\frac{3}{2}}\\  \end{array}⟧\begin{array}{c}1\\  \\ 0\end{array}+\begin{array}{c} \\ x\\  \end{array}⟧\begin{array}{c}1\\  \\ 0\end{array}=\frac{2}{3}\left({1}^{3/2}-{0}^{3/2}\right)+\left(1-0\right)=\frac{2}{3}+1=\frac{5}{3}{u}^{2}

Finalmente:

{\int }_{0}^{1}\left(\sqrt{x}+1\right)dx=1.66\dots {u}^{2}

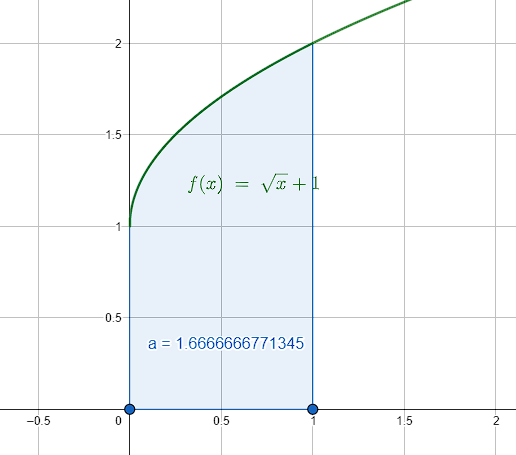
La respuesta correcta es el inciso a).

Reactivo 39

Determinar el área bajo la curva de la función {\int }_{-\pi }^{\pi }{x}^{2}\mathrm{sen}\left(x\right)dx sobre el intervalo [-\pi ,\pi ] .

1. 0
2. 1
3. \pi
4. 2\pi

Solución:

Examinando el integrando, queda claro que debemos aplicar el método de integración por partes para encontrar la primitiva. Primero integramos indefinidamente y luego aplicamos el segundo teorema fundamental del cálculo.

\int {x}^{2}\mathrm{sin}\left(x\right)dx

Seleccionamos a u como {x}^{2} y a dv como \mathrm{sin}\left(x\right)dx .

u={x}^{2}, dv=\mathrm{sin}\left(x\right)dx

Resolvemos.

du=2xdx, v=-\mathrm{cos}x

Aplicamos la fórmula de integración por partes.

\int {x}^{2}\mathrm{sin}\left(x\right)dx=-{x}^{2}\mathrm{cos}x+2\int x\mathrm{cos}xdx

Aplicamos de nuevo integración por partes.

{I}_{2}=\int x\mathrm{cos}xdx

u=x, dv=\mathrm{cos}xdx

du=dx, v=\mathrm{sin}x

{I}_{2}=x\mathrm{sin}x-\int \mathrm{sin}xdx=x\mathrm{sin}x+\mathrm{cos}x

Sustituimos en la integral original.

\int {x}^{2}\mathrm{sin}\left(x\right)dx=-{x}^{2}\mathrm{cos}x+2\left(x\mathrm{sin}x+\mathrm{cos}x\right)

\int {x}^{2}\mathrm{sin}\left(x\right)dx=-{x}^{2}\mathrm{cos}x+2x\mathrm{sin}x+2\mathrm{cos}x

Con la primitiva F\left(x\right)=-{x}^{2}\mathrm{cos}x+2x\mathrm{sin}x+2\mathrm{cos}x , aplicamos el teorema fundamental del cálculo.

I=F\left(\pi \right)-F\left(-\pi \right)

I=-{\left(\pi \right)}^{2}\mathrm{cos}\left(\pi \right)+2\left(\pi \right)\mathrm{sin}\left(\pi \right)+2\mathrm{cos}\left(\pi \right)+{\left(-\pi \right)}^{2}\mathrm{cos}\left(-\pi \right)-2\left(-\pi \right)\mathrm{sin}\left(-\pi \right)-2\mathrm{cos}\left(-\pi \right)

I={\pi }^{2}-2-{\pi }^{2}+2=0

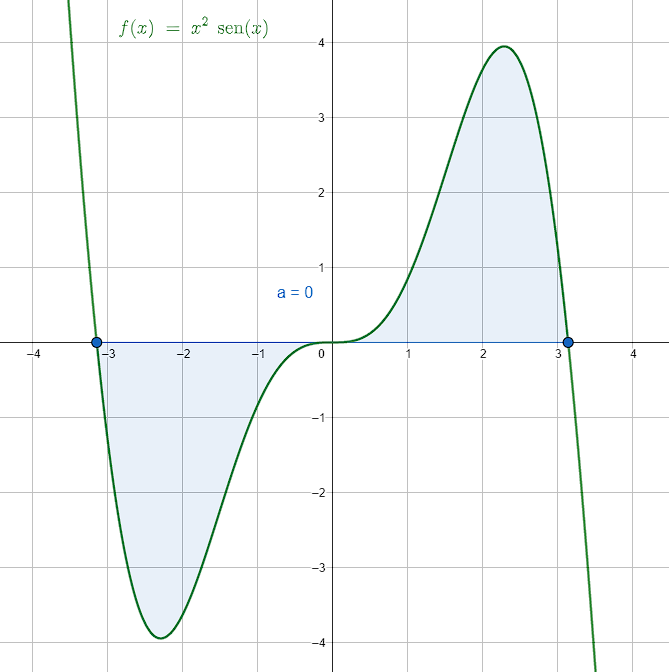
La respuesta correcta es el inciso a).

Reactivo 40

Determinar la longitud de arco de la gráfica que corresponde a la función f\left(x\right)=\frac{2}{3}{x}^{3/2}+1 sobre el intérvalo \left[0, 1\right] .

1. \frac{4}{3}\sqrt{2}-\frac{2}{3}
2. \frac{4}{3}\sqrt{2}+\frac{2}{3}
3. \frac{3}{4}\sqrt{2}-\frac{2}{3}
4. \frac{3}{4}\sqrt{2}+\frac{2}{3}

Solución:

La longitud de arco de una función f en el intervalo \left[a,b\right] , donde f es continua y derivable, se calcula como:

L={\int }_{0}^{1}\sqrt{1+{f}^{\text{'}}{\left(x\right)}^{2}}dx

Calculamos la derivada de f .

{f}^{\text{'}}\left(x\right)={\left(\frac{2}{3}{x}^{\frac{3}{2}}+1\right)}^{\text{'}}=\frac{2}{3}\cdot \frac{3}{2}{x}^{\frac{1}{2}}={x}^{\frac{1}{2}}

Sustituimos en la integral.

L={\int }_{0}^{1}\sqrt{1+{\left({x}^{\frac{1}{2}}\right)}^{2}}dx={\int }_{0}^{1}\sqrt{1+x}dx

Esta integral se resuelve con la fórmula para una potencia.

L={\int }_{0}^{1}{\left(1+x\right)}^{1/2}dx=\begin{array}{c}\\ \frac{2}{3}{\left(1+x\right)}^{3/2}\\ \end{array}⟧\begin{array}{c}1\\ \\ 0\end{array}

Evaluamos.

L=\frac{2}{3}\sqrt{{\left(1+1\right)}^{3}}-\frac{2}{3}=\frac{2}{3}\sqrt{8}-\frac{2}{3}

Finalmente:

L=\frac{4}{3}\sqrt{2}-\frac{2}{3}{u}^{2}

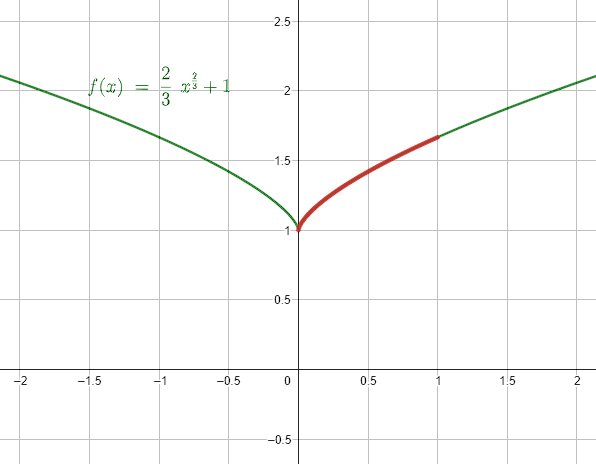
La respuesta correcta es el inciso a).