Examen simulacro UNAM 2024 área 2: Matemáticas 24 reactivos

¡Hola, aspirante! Con este examen simulacro de matemáticas para las carreras del área 2 de Ciencias Biológicas, Químicas y de la Salud de la UNAM, podrás poner a prueba ts conocimientos antes del examen de admisión real.

Vamos a resolver los primeros 12 reactivos, cuando termines puedes entrar a la parte 2 en el siguiente botón.

Reactivos del 13 al 24

Estructura del examen

El examen a la Universidad Nacional Autónoma de México tiene un total de 120 reactivos, de los cuales 24 pertenecen a matemáticas para el área 2.

¿Aún no conoces todos los detalles del ingreso a la UNAM?

Todo sobre el examen y la guía UNAM

En la siguiente tabla, encontrarás la estructura del examen a la UNAM para el área 2, con el total de reactivos por asignatura que deberás resolver.

Estructura examen área 2.

Temas Reactivos
Español 18
Matemáticas 24
Física 12
Química 13
Biología 13
Historia universal 10
Historia de México 10
Literatura 10
Geografía 10
Total 120
Conoce todo sobre los aciertos mínimos a la UNAM

La UNAM oferta unas 130 carreras, donde 31 de ellas pertenecen al área 2, y 9 poseen modalidad de ingreso indirecto.

Aparta tu lugar al primer grupo con 30% OFF

Curso UNAM 2025

Acceso total durante x12 meses
El curso cubre todos los temas del examen de admisión con clases en vivo y examenes simulacro.
Código: UNAM120
$4,000 MX
$2,800 MXN
Curso UNAM 2025

Simulador de matemáticas UNAM área 2

Te aconsejo resolverlos por tu cuenta antes de mirar la respuesta correcta. Es importante que estudies cada uno de los temas, tu calificación es proporcional al esfuerzo que hayas dedicado al prepararte.

Comenzamos con el simulador de matemáticas UNAM del área 2 de Ciencias Biológicas, Químicas y de la Salud.

Reactivo 1

Si 221 es el dividendo y 13 es el divisor en la ecuación, ¿cuánto valen el cociente c y el residuo r?

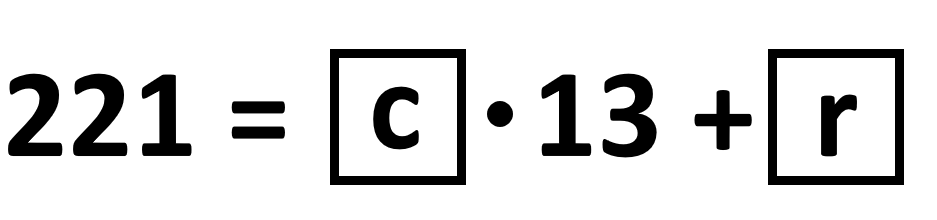
  1. c=15 y r=0
  2. c=16 y r=5
  3. c=17 y r=0
  4. c=18 y r=6

Respuesta correcta: c).

Reactivo 2

Factoriza la siguiente expresión.

{n}^{4}+{n}^{2}-2

  1. \left({n}^{2}-1\right)\left({n}^{2}+2\right)
  2. \left({n}^{2}-2\right)\left({n}^{2}+1\right)
  3. \left({n}^{2}-1\right)\left({n}^{2}-2\right)
  4. \left({n}^{2}+3\right)\left({n}^{2}+6\right)

Respuesta correcta: a).

Reactivo 3

Selecciona la expresión que corresponde a una identidad:

  1. \mathrm{sen}\left(x\right)>\frac{1}{2}
  2. \mathrm{sen}\left(x\right)=\frac{1}{2}x
  3. {\mathrm{sen}}^{2}\left(x\right)=1
  4. {\mathrm{sec}}^{2}\left(x\right)-{\mathrm{tan}}^{2}\left(x\right)=1

Respuesta correcta: d).

Reactivo 4

Las soluciones de la ecuación 14{x}^{2}-5x-1=0 son:

  1. {x}_{1}=-\frac{1}{7}, {x}_{2}=\frac{1}{2}
  2. {x}_{1}=\frac{1}{7}, {x}_{2}=-\frac{1}{2}
  3. {x}_{1}=\frac{1}{7}, {x}_{2}=\frac{1}{2}
  4. {x}_{1}=7, {x}_{2}=2

Respuesta correcta: a).

Reactivo 5

Selecciona la desigualdad que tiene por solución al siguiente conjunto. \left[-\frac{5}{2},\infty \right)

  1. 3x-1\ge 0
  2. 4x-3\ge 8
  3. 4x-3\ge 2x-8
  4. 4x-3\ge 2x

Respuesta correcta: c).

Reactivo 6

A partir del siguiente sistema de ecuaciones obtén el valor de x.

\begin{array}{c}6x+y=-5\\ -x+2y=3\end{array}

  1. x=-3
  2. x=-1
  3. x=1
  4. x=3

Respuesta correcta: b).

Reactivo 7

Determina el rango de la función:

f\left(x\right)={\left(x-1\right)}^{2}+2

  1. y\in R, y\ge 2
  2. x\in R, y\in R
  3. x\in R, x\ge 2
  4. y\in R, y\le 2

Respuesta correcta: a).

Reactivo 8

¿Cuál es el seno del ángulo B en el triángulo rectángulo siguiente?

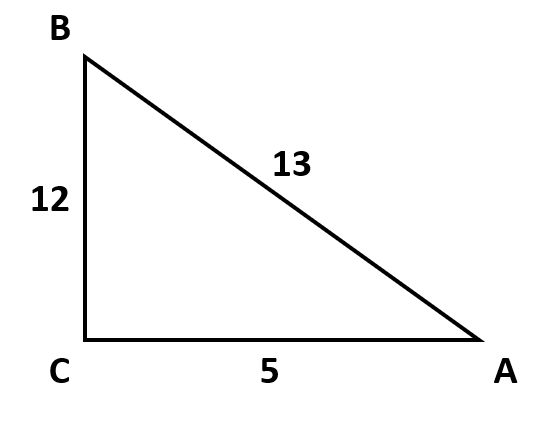
  1. \frac{5}{13}
  2. \frac{5}{12}
  3. \frac{12}{13}
  4. \frac{13}{12}

Respuesta correcta: a).

Reactivo 9

Selecciona la función que tiene un desplazamiento de fase de \pi  unidades a la izquierda.

  1. f\left(x\right)=\mathrm{sin}\left(\pi x\right)
  2. f\left(x\right)=\mathrm{sin}\left(x+\pi \right)
  3. f\left(x\right)=\mathrm{sin}\left(x-\pi \right)
  4. f\left(x\right)=\pi \mathrm{sin}\left(x\right)

Respuesta correcta: b).

Reactivo 10

¿Cuál es el dominio de la siguiente función?

f\left(x\right)=\sqrt{x+3}
  1. x\le -3
  2. x<-3
  3. x>-3
  4. x\ge -3

Respuesta correcta: d).

Reactivo 11

El punto medio del segmento que une a los puntos A\left(m+1,  3m\right) y B\left(2m-1,  m\right) es:

  1. \left(\frac{3}{2}, 2\right)
  2. \left(\frac{3m}{2}, 2m\right)
  3. \left(\frac{m}{3}, 2m\right)
  4. \left(\frac{3m}{2}, 4m\right)

Respuesta correcta: b).

Reactivo 12

La pendiente de la recta 4y+3x-5=0 es:

  1. -3
  2. -\frac{1}{4}
  3. -\frac{3}{4}
  4. 3

Respuesta correcta: c).

Temario matemáticas área 2

La lista contiene el temario de matemáticas para el área 2 de la UNAM. Es extenso, pero si planificas tus sesiones de estudio podrás cubrir todo el contenido.

  1. Operaciones con números reales, complejos y expresiones algebraicas 
    1. Números reales
    2. Números complejos
    3. Expresiones algebraicas
  2. Productos notables y factorización
    1. Binomio de Newton a+bn, n ∈N
    2. Teorema del residuo y del factor 
    3. Simplificación de fracciones algebraicas 
    4. Operaciones con fracciones algebraicas
  3. Ecuaciones
    1. Ecuación, identidad y propiedades de la igualdad 
    2. Ecuaciones de primer grado 
    3. Ecuaciones de segundo grado
  4. Desigualdades
    1. Desigualdad de primer grado en una variable y sus propiedades
  5. Sistemas de ecuaciones 
    1. Sistemas de dos ecuaciones lineales con dos incógnitas
    2. Sistemas de tres ecuaciones lineales con tres incógnitas
  6. Funciones algebraicas
    1. Dominio, contradominio y regla de correspondencia 
    2. Rango o imagen 
    3. Gráfica 
    4. Implícitas y explícitas 
    5. Crecientes y decrecientes 
    6. Continuas y discontinuas
    7. Álgebra de funciones
  7. Trigonometría
    1. Trigonometría básica
    2. Funciones trigonométricas
  8. Funciones exponenciales y logarítmicas
    1. Dominio y rango 
    2. Gráficas y asíntotas
  9. Recta
    1. Distancia entre dos puntos 
    2. Coordenadas de un punto que divide a un segmento de acuerdo con una razón dada 
    3. Pendiente de una recta 
    4. Formas de la ecuación de la recta y su gráfica 
    5. Condiciones de paralelismo y perpendicularidad 
    6. Distancia de un punto a una recta 
    7. Ecuaciones de las medianas, mediatrices y alturas de un triángulo. Puntos de intersección (ortocentro, circuncentro y baricentro)
  10. Circunferencia
    1. Circunferencia como lugar geométrico
    2. Forma ordinaria (canónica) y general de la ecuación de la circunferencia con centro en el origen
    3. Ecuación de la circunferencia con centro en (h, k) en las formas ordinaria y general 
    4. Elementos de una circunferencia
  11. Parábola
    1. Parábola como lugar geométrico 
    2. Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en el origen y el eje focal coincide con alguno de los ejes coordenados 
    3. Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en un punto cualquiera del plano y eje focal paralelo a alguno de los ejes coordenados 
    4. Elementos de una parábola
  12. Elipse
    1. Elipse como lugar geométrico 
    2. Relación entre los parámetros a, b y c 
    3. Formas ordinaria y general de la ecuación de la elipse con centro en el origen y eje focal sobre alguno de los ejes coordenados 
    4. Formas ordinaria y general de la ecuación de la elipse con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados 
    5. Elementos de una elipse
  13. Hipérbola
    1. Hipérbola como lugar geométrico 
    2. Relación entre los parámetros de la hipérbola a, b y c 
    3. Formas ordinaria y general de la ecuación de la hipérbola con centro en el origen y eje focal sobre alguno de los ejes coordenados 
    4. Formas ordinaria y general de la ecuación de la hipérbola con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados 
    5. Elementos de una hipérbola
  14. Ecuación general de segundo grado
    1. Las cónicas 
    2. Ecuación general de segundo grado 
    3. Criterios para identificar a la cónica que representa una ecuación de segundo grado 
    4. Traslación de ejes
  15. Límites
    1. Concepto intuitivo 
    2. Definición formal 
    3. Teoremas sobre límites 
    4. Obtención de límites
    5. Formas indeterminadas 
    6. Continuidad en un punto y en un intervalo
  16. La derivada
    1. Definición de derivada y sus notaciones 
    2. Obtención de derivadas 
    3. Regla de la cadena 
    4. Derivada de funciones implícitas 
    5. Derivadas sucesivas de una función 
    6. Interpretación geométrica y física 
    7. Ecuaciones de la tangente y de la normal a una curva 
    8. Cálculo de velocidad y aceleración de un móvil 
    9. Máximos y mínimos relativos de una función 
    10. Máximos y mínimos absolutos en un intervalo cerrado 
    11. Puntos de inflexión y de concavidad en una curva 
    12. Problemas de la vida cotidiana
  17. La integral
    1. Función integrable en un intervalo cerrado 
    2. Teoremas que justifican las propiedades de la integral de una función 
    3. Integral inmediata 
    4. Tabla de fórmulas de integración 
    5. Métodos de integración 
    6. Integral definida y su notación

¿Cómo estudiar matemáticas?

A continuación tienes algunas recomendaciones que puedes seguir a la hora de estudiar matemáticas.

  • Selecciona tu bibliografía. En la guía UNAM área 2 se recomienda bibliografía de consulta para matemáticas. No es necesario leerlas todas, pero algunos temas se explican mejor en unos textos que en otros.
  • Presta atención a la teoría. Las propiedades y los teoremas son las herramientas que usan las matemáticas para llegar a cualquier resultado.
  • Apóyate en otro libro si un tema es complejo de entender. Los autores suelen enfocarse en determinados aspectos a la hora de escribir sus textos, por esta razón, suelen desbordar demasiados detalles que pueden confundirnos al estudiar.
  • Practica con ejercicios de forma inteligente. Resolver problemas intentando cualquier cosa no es la mejor forma correcta de practicar tus conocimientos. Analiza el problema, comprende lo que te solicita, identifica las herramientas matemáticas para resolverlo.

Otros aspirantes leyeron