¡Hola aspirante! En este tutorial vamos a resolver paso a paso los primeros 11 reactivos de Matemáticas área 4, del 41 al 51, en la guía de las Humanidades y de las Artes de cara al examen de ingreso a la UNAM.

A continuación, te dejo un breve resumen con los puntos más importantes del examen de ingreso a la UNAM.
- Desarrollo: UNAM
- Área 4: Humanidades y de las Artes
- Materia: Matemáticas
- Reactivos: 120
- Tipo: Opción múltiple
- Duración: 3 horas
- Modalidades: Presencial
Te aconsejo hacerlos por tu cuenta antes de acceder a la solución. Es importante que comprendas cada uno de los temas que van para el examen, tu calificación depende del esfuerzo que dediques durante la preparación.
Estructura del examen
El examen de ingreso a la UNAM tiene una extensión total de 120 reactivos, de los cuales 22 pertenecen a la asignatura de matemáticas para el área 4 de las Humanidades y de las Artes.
¿Quieres conocer todos los detalles del examen a la UNAM?
En la siguiente tabla, encontrarás la estructura del examen a la UNAM por el área 4, con la asignatura y la cantidad de reactivos correspondientes.
Estructura examen área 4.
| Temas | Reactivos |
| Español | 18 |
| Matemáticas | 22 |
| Física | 10 |
| Química | 10 |
| Biología | 10 |
| Historia universal | 10 |
| Historia de México | 10 |
| Literatura | 10 |
| Geografía | 10 |
| Filosofía | 10 |
| Total | 120 |
¿Sabías que en área 4, la carrera con el mayor número de aciertos obligatorios es traducción con 108?
De las 29 carreras ofertadas por la UNAM para el área 4, Cinematografía cuenta con modalidad de ingreso indirecto, es decir, deberás cumplir una serie de requisitos extra para ingresar.
¿Cómo estudiar matemáticas?
Probablemente sea común para ti estudiar matemáticas resolviendo montones de ejercicios y leyendo unos pocos apuntes, pero eso debe cambiar. No es relevante la cantidad de ejercicios resueltos, lo realmente valioso será tu capacidad para analizar los problemas, abstraer los conceptos y aplicarlos sobre las situacionesreales.
Los siguientes consejos te permitirán estudiar matemáticas manteniendo presente lo anterior.
- Revisa la bibliografía recomendada en la guía unam área 1 y selecciona 2 o 3 textos de tu agrado. No es necesario que los leas por completo, algunos temas se explican mejor en unos textos que en otros. Asegúrate de tener suficiente contenido de calidad.
- Lee la teoría y resuelve los ejemplos. Por más simple que parezca una propiedad o un teorema, conocer su origen, demostración y aplicaciones te será de gran utilidad durante el examen. Hay problemas cuya solución rápida se da a través de un teorema.
- Si un tema parece difícil de comprender, búscalo en otro libro. Los autores suelen enfocarse en determinados temas a la hora de escribir sus textos, por esta razón, suelen desbordar demasiados detalles que, al ser principiantes, pueden confundirnos al estudiar. Te recomiendo tener más de un libro de consulta.
- Practica con ejercicios… pero de forma inteligente. Resolver un ejercicio intentando cualquier idea que pase por tu mente no es la mejor forma de practicar lo que has aprendido. Analiza el problema, comprende lo que te solicita, identifica las herramientas matemáticas para resolverlo y crea en tu cabeza un plan sistemático para resolverlo. Si no funciona, regresa al inicio y pregúntate ¿qué hice mal? ¿hay un concepto que no apliqué correctamente?
Temario matemáticas área 1
En la siguiente lista tienes el temario de matemáticas para el área 4 de Humanidades y de las Artes UNAM. Puede parecer extenso, pero si organizas tu tiempo podrás cubrir todos los temas. Puedes acceder a mayor información sobre el examen y la convocatoria UNAM haciendo click en este enlace.
- Operaciones con números reales, complejos y expresiones algebraicas
- Números reales
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Números complejos
- Suma y resta
- Multiplicación
- Expresiones algebraicas
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Operaciones con radicales
- Números reales
- Productos notables y factorización
- Binomio de Newton a+bn, n ∈N
- Teorema del residuo y del factor
- Simplificación de fracciones algebraicas
- Operaciones con fracciones algebraicas
- Ecuaciones
- Ecuación, identidad y propiedades de la igualdad
- Ecuaciones de primer grado
- Ecuaciones de segundo grado
- Desigualdades
- Desigualdad de primer grado en una variable y sus propiedades
- Sistemas de ecuaciones
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Métodos de solución
- Sistemas de tres ecuaciones lineales con tres incógnitas
- Métodos de solución (Regla de Cramer)
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Funciones algebraicas
- Dominio, contradominio y regla de correspondencia
- Rango o imagen
- Gráfica
- Implícitas y explícitas
- Crecientes y decrecientes
- Continuas y discontinuas
- Álgebra de funciones
- Trigonometría
- Trigonometría básica
- Medida de un ángulo (conversión de grados a radianes y de radianes a grados)
- Razones trigonométricas
- Resolución de triángulos rectángulos
- Ley de los Senos y Ley de los Cosenos
- Resolución de triángulos oblicuángulos
- Razones trigonométricas para un ángulo en cualquier cuadrante. Fórmulas de reducción
- Funciones trigonométricas
- El círculo trigonométrico
- Funciones trigonométricas directas
- Dominio y rango
- Periodo y amplitud
- Desfasamiento
- Asíntotas de la gráfica
- Trigonometría básica
- Funciones exponenciales y logarítmicas
- Dominio y rango
- Gráficas y asíntotas
- Recta
- Distancia entre dos puntos
- Coordenadas de un punto que divide a un segmento de acuerdo con una razón dada
- Pendiente de una recta
- Formas de la ecuación de la recta y su gráfica
- Condiciones de paralelismo y perpendicularidad
- Distancia de un punto a una recta
- Ecuaciones de las medianas, mediatrices y alturas de un triángulo. Puntos de intersección (ortocentro, circuncentro y baricentro)
- Circunferencia
- Circunferencia como lugar geométrico
- Formas ordinarias (canónica) y general de la ecuación de la circunferencia con centro en el origen
- Ecuación de la circunferencia con centro en (h, k) en las formas ordinaria y general
- Elementos de una circunferencia
- Parábola
- Parábola como lugar geométrico
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en el origen y el eje focal coincide con alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en un punto cualquiera del plano y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una parábola
- Elipse
- Elipse como lugar geométrico
- Relación entre los parámetros a, b y c
- Formas ordinaria y general de la ecuación de la elipse con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la elipse con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una elipse
- Hipérbola
- Hipérbola como lugar geométrico
- Relación entre los parámetros de la hipérbola a, b y c
- Formas ordinaria y general de la ecuación de la hipérbola con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la hipérbola con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una hipérbola
- Ecuación general de segundo grado
- Las cónicas
- Ecuación general de segundo grado
- Criterios para identificar a la cónica que representa una ecuación de segundo grado
- Traslación de ejes
Guía matemáticas UNAM área 4 resuelta
Vamos con el desarrollo paso a paso de los primeros 12 reactivos de matemáticas área 4, para la guía de la Universidad Nacional Autónoma de México del área de las Humanidades y de las Artes.
Reactivo 41
El resultado de 0.1709–2.91+1.1783 es:
- –4.1512
- –1.6592
- –4.2592
- –1.5608
Solución:
Debemos calcular las operaciones de suma y resta entre los números de la expresión. Recordemos que se inicia de izquierda a derecha, por lo tanto, primero se resuelve 0.1709 – 2.91 y el resultado se suma con 1.1783.
La primera operación es una resta entre un número menor y otro mayor. Se resta el mayor con el menor y al resultado se escribe con signo negativo.
Se completa con ceros a la derecha de las cifras decimales para realizar la resta.

El cero le quita prestado 1 al 9 para restarse con el 7.

La operación va quedando:
0.1709 – 2.91 + 1.1783=-2.7391+1.1783
Se resuelve la resta y se conserva el signo negativo porque 2.7391 es mayor que 1.1783.

El 3 no puede restarse con el 7, se le quita uno prestado al 7 de la derecha.

Finalmente:
-2.7391+1.1783=-1.5608
Concluimos indicando como respuesta correcta al inciso D.
Reactivo 42
Dos números están en razón \frac{3}{7} , si el menor de ellos es 189, ¿cuál es el otro?
- 525
- 519
- 441
- 386
Solución:
Analizando la razón del enunciado, se trata de una fracción propia, es decir, el numerador es menor que el denominador. Por esta razón, si el número menor es 189, el cociente se hace 189 sobre el número desconocido.
\frac{189}{x}=\frac{3}{7}
Acá tenemos dos opciones: comprobar cada una de las opciones o, despejar el valor de x . Debido a que el primer procedimiento puede ser tardado, vamos a despejar el valor del número mayor.
\frac{189}{x}=\frac{3}{7}\to x=\frac{\left(7\right)\left(189\right)}{3}
Se resuelve el producto del numerador.
x=\frac{\left(7\right)\left(189\right)}{3}=\frac{1323}{3}
Simplificado la fracción:
x=441
La respuesta correcta es la del inciso C.
Reactivo 43
¿Cuál es la factorización del siguiente trinomio {x}^{2}–11x+30 ?
- \left(x+5\right)\left(x+6\right)
- \left(x+1\right)\left(x+30\right)
- \left(x-5\right)\left(x+6\right)
- \left(x-5\right)\left(x-6\right)
Solución:
Debido a que el coeficiente de {x}^{2} es 1, podemos aplicar el truco de buscar dos números que sumen -11 y que multiplicados sean 30 para factorizar el trinomio. En este caso, podemos responder la pregunta analizando los incisos. El siguiente es un truco de examen.
Debido a que la suma de las cantidades desconocidas es un número negativo (-11) y la multiplicación es un número positivo (30), la única forma de que esto ocurra, es que ambas cantidades sean negativas. Según la ley de los signos:
\left(-\right)+\left(-\right)=-
\left(-\right)\times \left(-\right)=+
El único inciso cuyas raíces son negativas es el D. Por lo tanto, la respuesta correcta es la del inciso D.
Reactivo 44
Resuelve la siguiente operación algebraica.
\frac{{x}^{2}-7x+12}{\left({x}^{2}-16\right)\left(x-3\right)}
- \frac{1}{x-3}
- \frac{1}{x+4}
- \frac{x-3}{x+4}
- \frac{x-4}{x-3}
Solución:
Para encontrar la forma simplificada de la expresión, es necesario factorizar tanto al trinomio del numerador como a la diferencia de cuadrados del denominador.
El trinomio se factoriza con el truco de buscar dos números que sumen -7 y que multiplicados sean +12. Si multiplicamos -3 por -4 se obtiene +12, mientras que la suma algebraica es igual a -7. Por otra parte, a la diferencia de cuadrados se factoriza empleando la fórmula con el mismo nombre.
{x}^{2}-7x+12=\left(x-3\right)\left(x-4\right)
{x}^{2}-16=\left(x+4\right)\left(x-4\right)
Sustituimos en la expresión y simplificamos:
\frac{{x}^{2}-7x+12}{\left({x}^{2}-16\right)\left(x-3\right)}=\frac{\left(x-3\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)\left(x-3\right)}=\frac{1}{x+4}
Finalmente:
\frac{{x}^{2}-7x+12}{\left({x}^{2}-16\right)\left(x-3\right)}=\frac{1}{x+4}
La respuesta correcta es el inciso B.
Reactivo 45
La solución de la ecuación \frac{x}{4}+1=\frac{x}{2} es:
- x=1
- x=2
- x=4
- x=8
Solución:
Iniciamos agrupando los términos con x en el miembro izquierdo de la igualdad.
\frac{x}{4}+1=\frac{x}{2}\to \frac{x}{4}-\frac{x}{2}=-1
Resolvemos la resta de fracciones y despejamos el valor de x .
-\frac{x}{4}=-1\to \frac{x}{4}=1
\therefore x=4
La respuesta correcta es la del inciso C.
Reactivo 46
Encuentra el rango de valores para x , que satisface las siguientes desigualdades.
x-1<0
3\le x+5
- x<-2 ó 1\ge x
- -1\le x<2
- -2<x\le -1
- -2\le x<1
Solución:
El enunciado plantea un sistema de inecuaciones, cuya solución total será la intersección de los conjuntos de ambas inecuaciones. Siguiendo con lo anterior, debemos resolver por separado a las inecuaciones y luego intersecar los conjuntos obtenidos.
Primera inecuación.
x-1<0
{\mathrm{S}\mathrm{o}\mathrm{l}}_{1}:x<1
Segunda inecuación.
3\le x+5
Se resta x en ambos miembros de la desigualdad.
3-x\le x+5-x\to 3-x\le 5
Ahora, se resta 3 en ambos miembros.
3-x-3\le 5-3\to -x\le 2
Se multiplica ambos miembros por -1. El sentido de la desigualdad cambia.
-x\le 2\to x\ge -2
{\mathrm{S}\mathrm{o}\mathrm{l}}_{2}:x\ge -2
Ahora, se intersecan las soluciones.
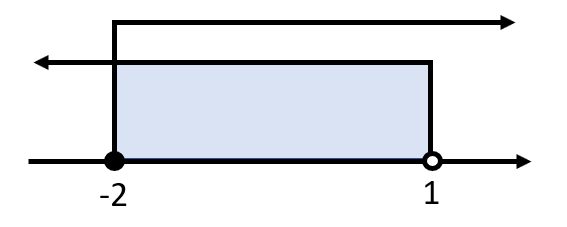
Finalmente:
-2\le x<1
La respuesta correcta se encuentra en el inciso D.
Reactivo 47
¿Cuál es la solución del siguiente sistema de ecuaciones?
3x+y=8
2x-4y=-4
- x=-2;y=2
- x=1;y=4
- x=2;y=-2
- x=2;y=2
Solución:
Para resolver el sistema de ecuaciones, se puede emplear cualquiera de los métodos: por igualación, reducción, sustitución e incluso métodos matriciales. En este caso, vamos a resolver el sistema de ecuación mediante eliminación.
Se multiplica la primera ecuación por 4 y se suma con la segunda.
4{E}_{1}:12x+4y=32
{E}_{2}:2x-4y=-4
4{E}_{1}+{E}_{2}:14x=28
Despejando el valor de x se obtiene:
x=2
Se sustituye el resultado en la primera ecuación se obtiene:
3\left(2\right)+y=8\to 6+y=8
y=8-6\to y=2
La solución del sistema de ecuaciones es:
x=2;y=2
Concluimos indicando como respuesta correcta al inciso D.
Reactivo 48
Obtén el dominio y el rango de la siguiente función.
y=\frac{-5}{-\sqrt{x+2}}
- \begin{array}{c}\mathrm{D}=x>-2\\ \mathrm{R}=y>0\end{array}
- \begin{array}{c}\mathrm{D}=x\ge -2\\ \mathrm{R}=y\ge 0\end{array}
- \begin{array}{c}D=x>-2\\ R=y\ge 0\end{array}
- \begin{array}{c}D=x<-2\\ R=y\le 0\end{array}
Solución:
El dominio de una función se calcula obteniendo el conjunto solución de todas las restricciones de la expresión. En este caso, tenemos a una fracción cuya restricción es que el denominador sea diferente de cero.
Por otra parte, existe una función radical de índice par (2) cuya restricción es que el radicando sea mayor o igual que cero. Debido a que no puede valer cero por la restricción de la fracción, el domino de la función viene expresado por:
x+2>0
Despejando se obtiene:
\mathrm{D}=x>-2
Para el rango, se debe calcular la inversa de la función y a dicho resultado calcularle el dominio. Cuando la función es sencilla y conocida, el rango se obtiene mediante análisis. En este caso, la función siembre dará valores positivos de y .
y=\frac{-5}{-\sqrt{x+2}}=y=\frac{5}{\sqrt{x+2}}
El numerador es constante, por lo tanto, la fracción dará un número grande cuando \sqrt{x+2} sea cercano a cero o un número pequeño cuando sea mayor que 5. El resultado nunca será cero, porque esto solo ocurre cuando x\to +\infty .
A partir de este análisis, concluimos que el rango se encuentra acotado entre cero abierto e infinito.
\mathrm{R}=y>0
Finalmente:
\begin{array}{c}D=x>-2\\ R=y>0\end{array}
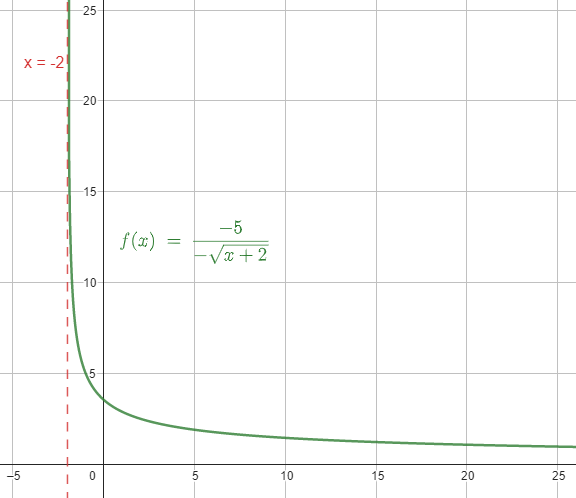
Se concluye indicando como respuesta correcta al inciso A.
Reactivo 49
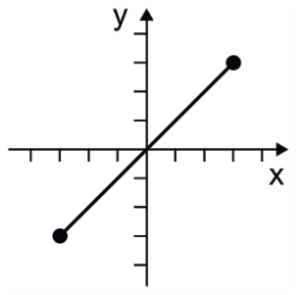
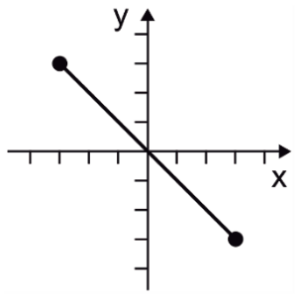
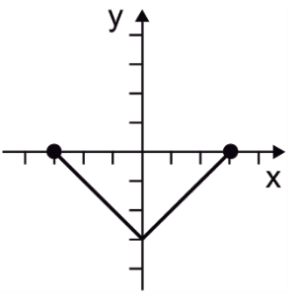
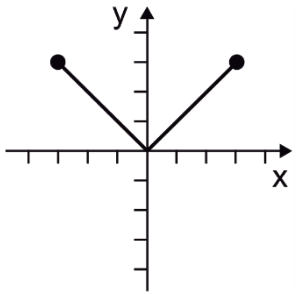
¿Cuál es la gráfica de f\left(x\right)=\left|x\right| con x\in \left[–\mathrm{3,3}\right] ?
Solución:
La función valor absoluto, permite obtener valores positivos sin importar el signo de la expresión dentro de las barras. La expresión en este caso es x , que representa una línea recta de pendiente positiva.
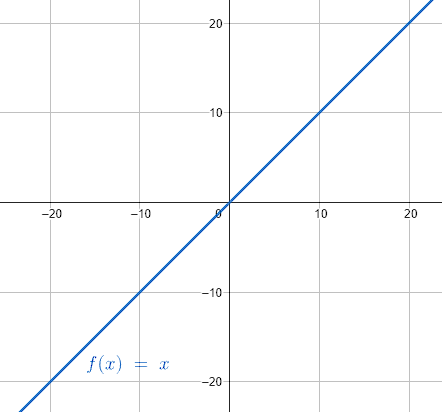
Debido a que entre -\infty hasta 0 los valores de la recta son negativos, al introducirlos en la función valor absoluto, se convierten en cantidades positivas. Esto provoca que la gráfica de \left|x\right| sea una “V” con vértice en x=0 .
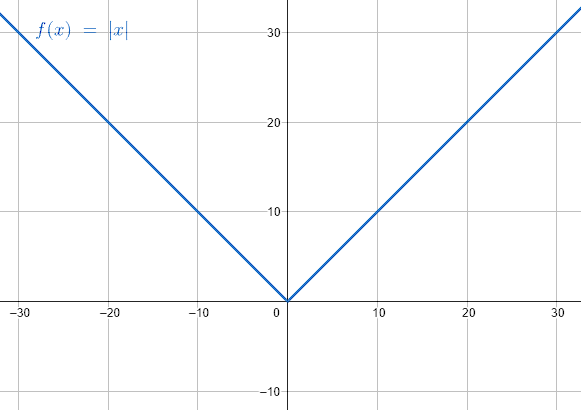
Acotando la función entre -3 y 3 nos queda:
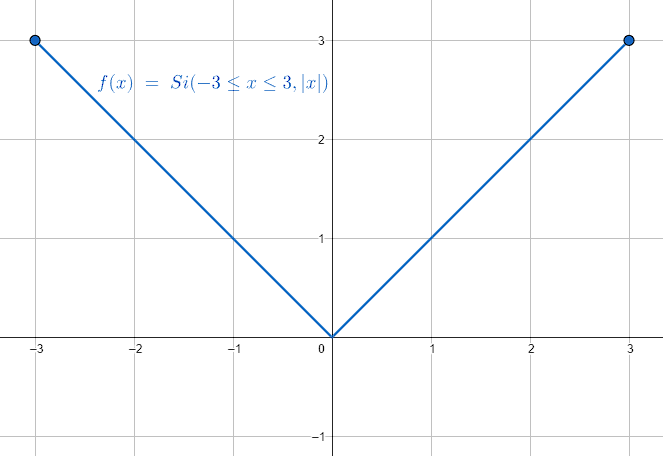
Comparando con los incisos, concluimos que la respuesta correcta es el D.
Reactivo 50
¿Cuál de las siguientes funciones tienen un comportamiento creciente?
- f\left(x\right)=-3x
- f\left(x\right)={3}^{-x}
- f\left(x\right)=\frac{3}{x}
- f\left(x\right)={x}^{3}
Solución:
En términos generales, decimos que una función es creciente cuando y aumenta para aumentos de x y decreciente si y decrece para aumentos de x . Otra forma de decir que una función es creciente o decreciente, pasa por examinar su grafica.
Si al desplazarnos de izquierda a derecha la gráfica va de arriba hacia abajo decrece, si va de menos a más crece. Basados en lo anterior y sin emplear la gráfica de las funciones, analizaremos cuál de ellas es creciente.
Primera función.
f\left(x\right)=-3x
Es una función lineal con pendiente negativa m=-3 por consiguiente, es decreciente para cualquier incremento de x .
Segunda función.
f\left(x\right)={3}^{-x}
Si aplicamos propiedades de la potenciación, la segunda función puede escribirse como:
f\left(x\right)={3}^{-x}=\frac{1}{{3}^{x}}
Corresponde a una función potencial que tiene valores más cercanos a cero a medida que x se acerca a +\infty , por tanto, es una función decreciente.
Tercera función.
f\left(x\right)=\frac{3}{x}
El dominio de esta función son todos los reales excepto en x=0 , punto en el que presenta una discontinuidad. Debemos analizar su crecimiento/decrecimiento para dos intervalos: \left(-\infty ,0\right) y \left(0,\infty \right) .
En el primer intervalo, la función tiene valores más negativos a medida que x se acerca a cero, punto en el que por la izquierda se va hacia -\infty . Para el segundo, en cero por la derecha la función decrece desde infinito positivo hasta hacerse cada vez más pequeña a medida que x incrementa.
Concluimos entonces que la función 3 es decreciente en sus dos intervalos de existencia.
Cuarta función.
f\left(x\right)={x}^{3}
La última función es de tercer grado e incrementa rápidamente su valor cuando nos movemos de izquierda a derecha. La cuarta función es la única de tipo creciente en los 4 incisos.
Seleccionamos como respuesta correcta la opción D.
Reactivo 51
Convierte el valor de un ángulo que mide \frac{2}{4}\pi radianes a grados.
- 270°
- 90°
- 60°
- 240°
Solución:
Para pasar un ángulo que se encuentra en radianes a grados, empleamos la siguiente relación:
180°\to \pi \mathrm{r}\mathrm{a}\mathrm{d}
Hacemos una sencilla regla de tres.
\pi \mathrm{r}\mathrm{a}\mathrm{d}\to 180°
\frac{2}{4}\pi \to x
Entonces:
x=\frac{\frac{2}{4}\pi *180°}{\pi }=\frac{2}{4}*180°=90°
Concluimos que \frac{2}{4}\pi es igual a 90°.
Seleccionamos como respuesta correcta la opción B.