¡Llegamos a la última parte aspirante! Vamos con la solución de la segunda parte de los reactivos de matemáticas área 4, en este caso del 52 al 62, de la guía de las Humanidades y de las Artes como preparación al examen de ingreso a la UNAM.

El siguiente resumen indica los puntos clave el examen UNAM:
- Desarrollo: UNAM
- Área 4: Humanidades y de las Artes
- Materia: Matemáticas
- Reactivos: 120
- Tipo: Opción múltiple
- Duración: 3 horas
- Modalidades: Presencial
¡Felicidades por llegar hasta aquí aspirante! Matemáticas muchas veces se entiende como una asignatura de fórmulas y despejes, en ella se encuentran los modelos para comprender el mundo que nos rodea.
Guía matemáticas UNAM área 4 resuelta
Vamos con los últimos 11 ejercicios de matemáticas de la guía del Área 4 de las Humanidades y de las Artes de la UNAM. Recuerda tomar descansos entre grupos de ejercicios, esto también forma parte del proceso de aprendizaje.
Esta guía no posee reactivos de todos los temas que van para el examen. Te invito a continuar aprendiendo con el resto de guías resueltas de la UNAM, maratones de reactivos y clases.
Reactivo 52
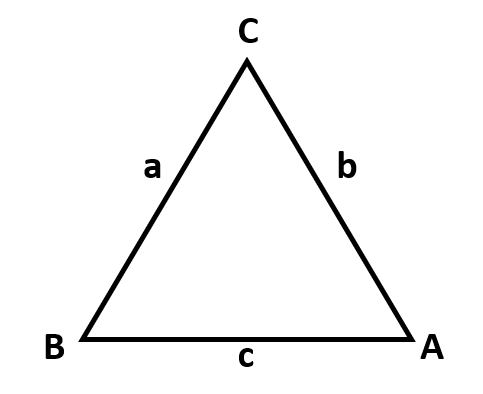
¿Cuál de las siguientes expresiones se obtiene de la Ley de los Senos?
- \frac{\mathrm{sen}A}{a}=\frac{\mathrm{sen}B}{b}
- \frac{\mathrm{sen}A}{b}=\frac{\mathrm{sen}B}{a}
- \frac{\mathrm{sen}A}{c}=\frac{\mathrm{sen}B}{a}
- \frac{\mathrm{sen}B}{c}=\frac{\mathrm{sen}A}{b}
Solución:
La ley de los senos es una relación trigonométrica que establece que el cociente entre el seno de cualquiera de los ángulos internos a un triángulo y su lado opuesto es igual para los tres ángulos y lados opuestos. La definición operación de la Ley de los Senos según el triángulo de la imagen es:
\frac{\mathrm{sen}A}{a}=\frac{\mathrm{sen}B}{b}=\frac{\mathrm{sen}C}{c}
Examinando los incisos, la única igualdad que corresponde con la Ley de Senos es la de la opción A.
\frac{\mathrm{sen}A}{a}=\frac{\mathrm{sen}B}{b}
Concluimos que la respuesta correcta es la opción A.
Reactivo 53
El dominio D y el rango R de la función f\left(x\right)=\frac{{e}^{x}}{-5} son
- D=\left(-\mathrm{\infty },0\right);R=\left(-\mathrm{\infty },\mathrm{\infty }\right)
- D=\left(0,\mathrm{\infty }\right);R=\left(-\mathrm{\infty },\mathrm{\infty }\right)
- D=\left(-\mathrm{\infty },\mathrm{\infty }\right);R=\left(0,\mathrm{\infty }\right)
- D=\left(-\mathrm{\infty },\mathrm{\infty }\right);R=\left(-\mathrm{\infty },0\right)
Solución:
El dominio de una función es el conjunto de valores de x que, sustituidos en su regla de correspondencia, dan como resultado una imagen para f . Por otro lado, el rango es el conjunto de valores que corresponden a las imágenes de la función.
El cálculo de ambos conjuntos se resume en aplicar restricciones para que los resultados existan y sean finitos. Para el dominio no existe ninguna restricción, ya que una función potencial puede recibir como valor de entrada cualquier número real, por ende:
D=\left(-\infty ,\infty \right)
El rango se calcula primero determinando la inversa de la función y luego aplicando las mismas restricciones a y .
Inversa de f .
y=\frac{{e}^{x}}{-5}\to {e}^{x}=-5y
\therefore x=\mathrm{ln}\left(-5y\right)
La restricción para el argumento de una función logarítmica, es que sea mayor que cero.
-5y>0
\therefore y<0
El rango de f es el conjunto de valores de la imagen que son menores a cero.
R=\left(-\infty ,0\right)
Concluimos que:
D=\left(-\infty ,\infty \right); R=\left(-\infty ,0\right)
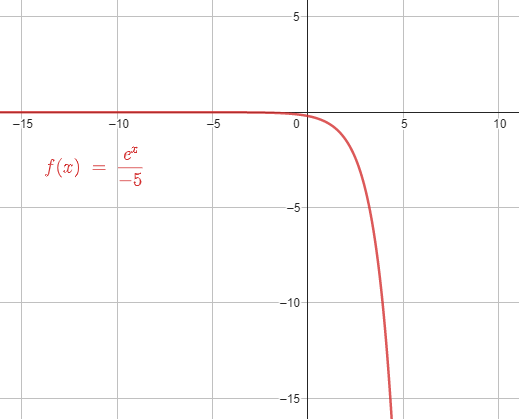
Comparando con las opciones, concluimos que la respuesta correcta es el inciso D.
Reactivo 54
¿Cuál es la ecuación de la asíntota vertical de la función f\left(x\right)=2\mathrm{log}\left(x-3\right) ?
- x=3
- y=-3
- x=-3
- y=3
Solución:
Las asíntotas son rectas a las que se aproxima una función, pero nunca se tocan. Dicho de otra forma, la distancia entre la recta y la función tiende a cero cuando x o y tienden a cierto valor.
Existen tres tipos de asíntotas: horizontales (respecto a y ) verticales (respecto a x ) y oblicuas (respecto de ambas variables). Para la función del enunciado, la asíntota vertical se encuentra en el valor de indeterminación del logaritmo base 10, es decir, cuando el argumento es igual a cero.
x-3=0
Despejando se obtiene:
x=3
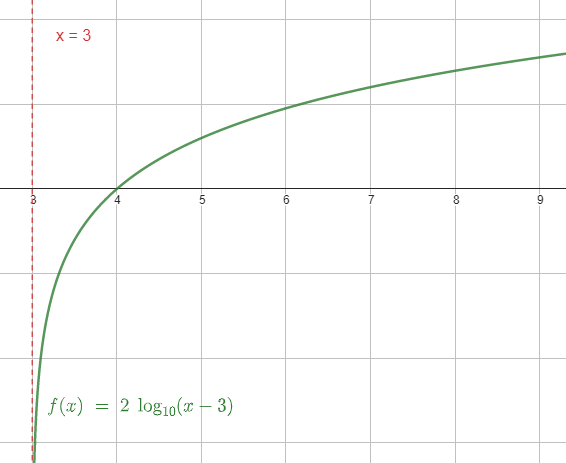
La respuesta correcta se encuentra en el inciso A.
Reactivo 55
¿Cuál es la distancia entre los puntos A\left(-7, -2\right) y B\left(2, 7\right) ?
- 162
- \sqrt{50}
- \sqrt{162}
- 50
Solución:
Para calcular la distancia entre dos puntos en el plano, empleamos la siguiente ecuación derivada del Teorema de Pitágoras.
d\left(A, B\right)=\sqrt{{\left({x}_{a}-{x}_{b}\right)}^{2}+{\left({y}_{a}-{y}_{b}\right)}^{2}}
Solo debemos sustituir las coordenadas correspondientes en la ecuación y calcular el valor numérico.
d\left(A, B\right)=\sqrt{{\left(-7-2\right)}^{2}+{\left(-2-7\right)}^{2}}=\sqrt{81+81}
d\left(A, B\right)=\sqrt{162}=12.7279
Podemos verificar este resultado de forma gráfica.
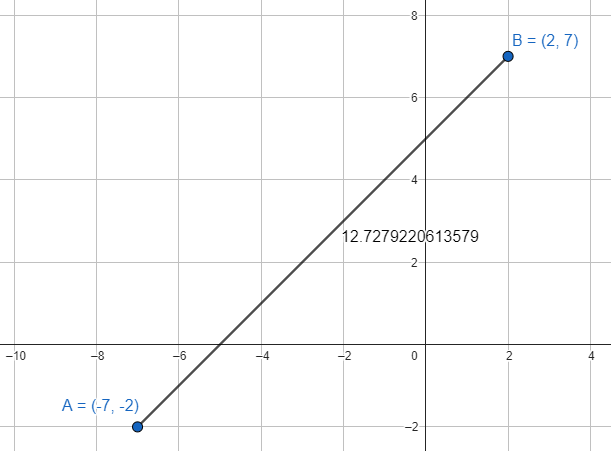
La respuesta correcta es la opción C.
Reactivo 56
¿Cuál es la pendiente de la recta que pasa por los puntos A(3, 2) y B(1, 5) ?
- 3
- \frac{3}{2}
- 1
- -\frac{3}{2}
Solución:
La pendiente de la recta que pasa por dos puntos se calcula como:
m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}
Sustituimos como \left({x}_{2},{y}_{2}\right)=\left(\mathrm{3,2}\right) y \left({x}_{1},{y}_{1}\right)=\left(\mathrm{1,5}\right) .
m=\frac{2-5}{3-1}=\frac{-3}{2}
La pendiente de la recta que pasa por los puntos es igual a -\frac{3}{2} .
Escogemos como respuesta correcta al inciso D.
Reactivo 57
¿Cuál de las siguientes ecuaciones corresponde a una circunferencia con centro en el origen y radio 2?
- {x}^{2}+{y}^{2}-4=0
- {x}^{2}+{y}^{2}-2=0
- {x}^{2}-{y}^{2}-2=0
- {x}^{2}-{y}^{2}-4=0
Solución:
Las circunferencias de los incisos se encuentran expresadas en la forma general. Debido a que en ninguna se observan los términos lineales de x y y , sabemos que todas se encuentran centradas en el origen.
Por otro lado, una circunferencia tiene los términos cuadráticos positivos, con esto se descartan a los incisos C y D. Finalmente, el término independiente corresponde con el cuadrado del radio. Solo la circunferencia del inciso A tiene como radio 2 unidades.
{r}^{2}=4\to r=2
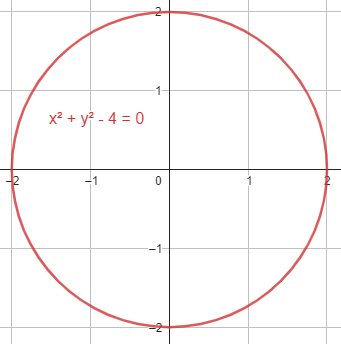
La respuesta correcta se encuentra en el inciso A.
Reactivo 58
Determina el centro y el radio de la circunferencia a partir de su ecuación.
{\left(x+4\right)}^{2}+{\left(y-6\right)}^{2}=49
- C(-4, 6); r=7
- C(4, –6); r=7
- C\left(–4, 6\right); r=49
- C(4, –6); r=49
Solución:
A partir de la ecuación ordinaria de una circunferencia {\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2} , sabemos que el centro es el punto \left(h, k\right) y que el radio al cuadrado viene representado por el término independiente {r}^{2} .
Llevando lo anterior a la ecuación del enunciado:
\left(h,k\right)=\left(-\mathrm{4,6}\right)
{r}^{2}=49\to r=7
Finalmente:
C\left(-\mathrm{4,6}\right);r=7
Comparando con los incisos, concluimos que la respuesta correcta es el A.
Reactivo 59
Calcula el vértice de la parábola {\left(y-3\right)}^{2}=12x-24 .
- V=\left(\mathrm{2,3}\right)
- V=\left(\mathrm{3,2}\right)
- V=\left(-3,-2\right)
- V=\left(-2,-3\right)
Solución:
La parábola del enunciado tiene situado el eje focal de forma horizontal, debido a que la variable y es quien se encuentra elevada al cuadrado. La forma canónica de una parábola horizontal es:
4p\left(x-h\right)={\left(y-k\right)}^{2}
Si extraemos factor común 12 del miembro de la derecha, obtenemos la forma ordinaria de la parábola.
{\left(y-3\right)}^{2}=12\left(x-2\right)
Finalmente, el vértice de la parábola es:
V\left(2, 3\right)
Respuesta correcta: opción A.
Reactivo 60
Determina las coordenadas de los focos de una elipse cuya ecuación es 9{x}^{2}+{y}^{2}=9 .
- {F}_{1}=\left(-\sqrt{8},0\right);{F}_{2}=\left(\sqrt{8},0\right)
- {F}_{1}=\left(-\sqrt{10},0\right);{F}_{2}=\left(\sqrt{10},0\right)
- {F}_{1}=\left(0,-\sqrt{8} \right);{F}_{2}=\left(0, \sqrt{8}\right)
- {F}_{1}=\left(0,-\sqrt{10} \right);{F}_{2}=\left(0, \sqrt{10}\right)
Solución:
Primero, dividimos entre 9 a toda la expresión para obtener la forma ordinaria de la elipse centrada en el origen.
\frac{9{x}^{2}}{9}+\frac{{y}^{2}}{9}=\frac{9}{9}\to {x}^{2}+\frac{{y}^{2}}{9}=1
Se trata de una elipse con eje focal vertical, porque el semieje mayor se encuentra dividiendo a la variable y . Para calcular las coordenadas de los focos, se emplea la siguiente ecuación:
{F}_{\mathrm{1,2}}=\left(h, k\pm c\right)
Donde h y k son las coordenadas del centro y c la semi distancia focal que se calcula como:
c=\sqrt{{a}^{2}-{b}^{2}}
De la ecuación del enunciado sabemos que: {a}^{2}=9 y {b}^{2}=1 .
c=\sqrt{9-1}=\sqrt{8}
Finalmente, las coordenadas de los focos son:
{F}_{1}=\left(0, -\sqrt{8}\right); {F}_{2}=\left(0, \sqrt{8}\right)
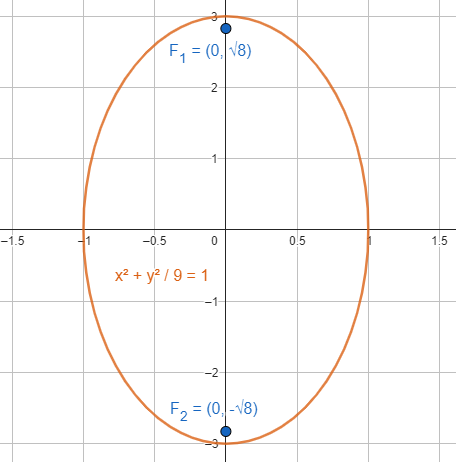
La respuesta correcta se encuentra en el inciso C.
Reactivo 61
Lugar geométrico en el plano cartesiano en el que el valor absoluto de la diferencia de sus distancias a dos puntos fijos en el mismo plano resulta siempre igual a una constante, positiva y menor que la distancia entre dichos puntos fijos.
- Circunferencia.
- Parábola.
- Elipse.
- Hipérbola.
Solución:
La definición analítica de una hipérbola, es el punto cuyo valor absoluto de la diferencia de las distancias respecto a los focos, es igual a una constante y menor que la distancia entre los focos.
\left|\left|{F}_{1}P\right|-\left|{F}_{2}P\right|\right|=2a
\left|{F}_{1}{F}_{2}\right|<2a
Dichos focos son puntos fijos, por tanto, teniendo en cuenta el enunciado y examinando los incisos, concluimos que la respuesta correcta se encuentra en el D.
Reactivo 62
Al trasladar la circunferencia {x}^{2}+{y}^{2}-36=0 al centro C\left(-\mathrm{2,4}\right) , ¿cuál sería su ecuación?
- {\left(x-4\right)}^{2}+{\left(y+16\right)}^{2}=36
- {\left(x+4\right)}^{2}+{\left(y-16\right)}^{2}=36
- {\left(x+2\right)}^{2}+{\left(y-4\right)}^{2}=36
- {\left(x-2\right)}^{2}+{\left(y+4\right)}^{2}=36
Solución:
La ecuación ordinaria de una circunferencia con centro fuera del origen es:
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
Donde h y k son las coordenadas del centro y {r}^{2} es el cuadrado del radio. Teniendo en cuenta le ecuación del enunciado, su centro se encuentra en el origen.
{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}=36
Sustituyendo las coordenadas actuales por las del nuevo centro nos queda:
{\left(x+2\right)}^{2}+{\left(y-4\right)}^{2}=36
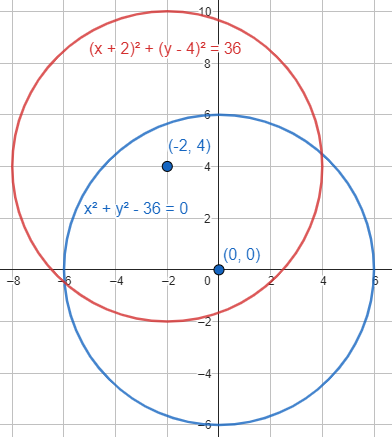
La respuesta correcta es el inciso C.


