Guía UNAM LCG | Módulo de Matemáticas de ciencias genómicas

Si vas a presentar el examen a la licenciatura en ciencias genómicas de la modalidad de ingreso indirecto, en este artículo vamos a resolver la guía del examen de admisión interno en el módulo de matemáticas.

Recuerda que para ingresar a esta licenciatura es necesario que primero apliques a la convocatoria vigente de la UNAM, y resultes seleccionado en alguna de las carreras de origen, puedes aplicar a cualquier carrera del área I o II.

Requisitos de ingreso:

La licenciatura se oferta en el centro de ciencias genómicas y en la Escuela Nacional de Estudios Superiores Juriquilla.

Consulta los otros temas del examen:

• Guía UNAM LCG | Módulo de Química de Ciencias Genómicas
• Guía UNAM LCG | Módulo de Biología de Ciencias Genómicas

Reactivo 1

Harry, un simpático perro labrador, se toma el 45% de una cubeta de agua al día. Clara, una amable perra gran danés, se toma el 80% de una cubeta de agua al día. Los dueños de Harry y Clara salieron de vacaciones y los dejaron solos en la casa. Olvidaron dejarles agua, pero la alberca estaba llena y tomaron agua de la alberca. Si la alberca llena contiene 1250 cubetas de agua y al terminar las vacaciones Harry y Clara consumieron una 50va parte, ¿cuánto tiempo duraron las vacaciones?

1. 10 días
2. 15 días
3. 20 días
4. 25 días
5. 50 días

Solución:

Para calcular el tiempo que los dueños de Harry y Clara han estado de viaje, debemos calcular la cantidad de agua que ambos caninos consumieron durante esos días y luego dividirla por la razón de cubetas por día que toman los dos.

Comenzamos dividiendo el volumen de la alberca en cubetas de agua por 50, ya que esta es la cantidad de agua que tomaron Harry y Clara.

\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{a}\mathrm{g}\mathrm{u}\mathrm{a}=\frac{1250\mathrm{ }\mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}}{50}=25 \mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}

Ahora, la razón de consumo de agua de ambos caninos por días es igual a la suma de las razones de cada uno.

\mathrm{C}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{H}\mathrm{a}\mathrm{r}\mathrm{r}\mathrm{y}\mathrm{ }\mathrm{y}\mathrm{ }\mathrm{C}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{a}=\mathrm{C}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}\mathrm{ }\mathrm{H}\mathrm{a}\mathrm{r}\mathrm{r}\mathrm{y}+\mathrm{C}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}\mathrm{ }\mathrm{C}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{a}

\mathrm{C}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{H}\mathrm{a}\mathrm{r}\mathrm{r}\mathrm{y}\mathrm{ }\mathrm{y}\mathrm{ }\mathrm{C}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{a}=\frac{45\mathrm{\%}\mathrm{ }\mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}}{\mathrm{d}\mathrm{í}\mathrm{a}}+\frac{80\mathrm{\%}\mathrm{ }\mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}}{\mathrm{d}\mathrm{í}\mathrm{a}}

Convertimos ambas razones de porcentaje a su equivalente en cubetas dividiendo por 100.

\mathrm{C}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{H}\mathrm{a}\mathrm{r}\mathrm{r}\mathrm{y}\mathrm{ }\mathrm{y}\mathrm{ }\mathrm{C}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{a}=0.45\frac{\mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}}{\mathrm{d}\mathrm{í}\mathrm{a}}+0.8\frac{\mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}}{\mathrm{d}\mathrm{í}\mathrm{a}}=1.25 \frac{\mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}}{\mathrm{d}\mathrm{í}\mathrm{a}}

Para obtener días, dividimos el equivalente en 25 cubetas que calculamos al principio por la razón de Harry y Clara.

\mathrm{D}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{ó}\mathrm{n}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{ }\mathrm{v}\mathrm{i}\mathrm{a}\mathrm{j}\mathrm{e}=\frac{25\mathrm{ }\mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}}{1.25 \frac{\mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}}{\mathrm{d}\mathrm{í}\mathrm{a}}}=20 \mathrm{d}\mathrm{í}\mathrm{a}\mathrm{s}

Concluimos entonces que los dueños de Harry y Clara estuvieron de viaje por 20 días. Seleccionamos como correcta la opción c).

Reactivo 2

Para cada reacción de un experimento se requiere: 196 ng de plásmido, 51 ng de molécula G, 1 µl de enzima y buffer para completar 20 µl. El plásmido está en una solución con 49 ng/µl y la molécula G en una solución con 34 ng/µl. Se usaron 108 µl de buffer.

¿Cuántas reacciones se realizaron?

1. 4
2. 5
3. 8
4. 10
5. 12

Solución:

Aunque el enunciado haga parecer que el problema es más complejo y necesitamos recurrir a conceptos de química, la verdad es que solo debemos ser consistentes con las unidades de las cantidades que vamos a operar.

No podemos tomar los nano gramos de plásmido y molécula G, sumarlo con el volumen de la enzima y luego restarlo con los 20 micro litros que debe tener la preparación total para obtener el volumen de buffer. Es incorrecto porque no podemos operar volumen con masas, al igual que no podemos restar pesos con dólares de forma directa, necesitamos un factor de conversión.

En este caso, nuestro factor de conversión para el plásmido y la molécula G son 49 ng/µl y 34 ng/µl respectivamente, que nos permitirán llevar nano gramos a micro litros y así operar consistentemente las cantidades.

Convertiremos.

\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{p}\mathrm{l}\mathrm{á}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{o}=\frac{196\mathrm{ }\mathrm{n}\mathrm{g}}{49\mathrm{ }\mathrm{n}\mathrm{g}/\mathrm{\mu }\mathrm{l}}=4 \mathrm{\mu }\mathrm{l}

\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{ú}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{é}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{ }\mathrm{G}=\frac{51\mathrm{ }\mathrm{n}\mathrm{g}}{34\mathrm{ }\mathrm{n}\mathrm{g}/\mathrm{\mu }\mathrm{l}}=1.5\mathrm{ }\mathrm{\mu }\mathrm{l}

Ahora, con estos volúmenes debemos calcular el volumen de buffer que se emplea por cada preparación, ya que el ejercicio nos dice que se utilizaron 108 micro litros de buffer para preparar todas las reacciones, si dividimos 108 entre los litros de buffer por reacción obtendremos la cantidad de reacciones.

{V}_{t}={V}_{p}+{V}_{G}+{V}_{e}+{V}_{b}\to {V}_{b}=20 \mathrm{\mu }\mathrm{l}-4 \mathrm{\mu }\mathrm{l}-1.5\mathrm{ }\mathrm{\mu }\mathrm{l}-1\mathrm{ }\mathrm{\mu }\mathrm{l}

\therefore {V}_{b}=13.5 \mathrm{\mu }\mathrm{l} \mathrm{p}\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{i}\mathrm{ó}\mathrm{n}

Dividimos para obtener el número de reacciones totales.

\mathrm{N}°\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{s}=\frac{108\mathrm{ }\mathrm{\mu }\mathrm{l}}{13.5\mathrm{ }\mathrm{\mu }\mathrm{l}}=8 \mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{s}

Se realizaron 8 reacciones durante el experimento.

Concluimos indicando como correcta la opción c).

Reactivo 3

Al final de cada semana el volumen de agua de un lago aumenta un 20% con respecto al volumen que tenía al inicio de la semana. Los sapos empezarán a aparecer cuando el volumen del lago sea al menos el doble del que tiene actualmente. ¿En cuántas semanas empezarán a aparecer los sapos?

1. Una
2. Dos
3. Tres
4. Cuatro
5. Cinco

Solución:

Este problema consta en ir incrementando porcentualmente determinado valor cada cierto período de tiempo, donde tanto los incrementos como el período de tiempo son constantes. Examinando otros temas de la Aritmética, nos damos cuenta que es similar el interés simple.

Tenemos una determinada cantidad de dinero inicial P , que va incrementando un cierto interés porcentual i durante n períodos constantes hasta obtener una cantidad de dinero S mayor que P . La ley del interés simple se escribe como:

S=P\left(1+ni\right)

En este caso, P es el volumen inicial del lago al que llamaremos {V}_{p} . S es el volumen luego de transcurridas las semanas {V}_{s} . n son las semanas, las cuales llamaremos de la misma forma e i corresponde al porcentaje de incremento en volumen del lago, denominado {\%}_{v} . Sustituyendo en la fórmula:

{V}_{s}={V}_{p}\left(1+n{\%}_{v}\right)

Queremos saber cuando {V}_{s} es el doble de {V}_{p} , escrito de otra manera: {V}_{s}=2{V}_{p} .

2{V}_{p}={V}_{p}\left(1+n{\%}_{v}\right)

Despejamos a n y sustituimos.

n=\frac{1}{{\%}_{v}}=\frac{1}{0.2}=5 \mathrm{s}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{a}\mathrm{s}

El lago duplicará su volumen en cinco semanas.

Escogemos como correcta la opción e).

Reactivo 4

Si {\mathrm{l}\mathrm{o}\mathrm{g}}_{3}\left(y\right)-{\mathrm{l}\mathrm{o}\mathrm{g}}_{3}\left(x\right)=\mathrm{s}\mathrm{e}\mathrm{n}\left(\pi \right) y {\mathrm{l}\mathrm{o}\mathrm{g}}_{5}\left(x\right)=2 , ¿Cuánto vale y ?

1. 25
2. 9
3. 5
4. 3
5. Cero

Solución:

Para calcular el valor solicitado, primero debemos encontrar el valor de x a partir de la segunda igualdad. Aplicamos la definición de logaritmo en sentido contrario.

{\mathrm{log}}_{b}n=x\to {b}^{x}=n

Llevamos esto a la segunda igualdad.

{\mathrm{log}}_{5}\left(x\right)=2\to {5}^{2}=x

Resolvemos la potencia:

x=25

Sustituimos en la primera ecuación.

{\mathrm{l}\mathrm{o}\mathrm{g}}_{3}\left(y\right)-{\mathrm{l}\mathrm{o}\mathrm{g}}_{3}\left(25\right)=\mathrm{s}\mathrm{e}\mathrm{n}\left(\pi \right)

De los conceptos de trigonometría, sabemos que el seno de pi es igual a cero. Aplicamos también la propiedad del logaritmo del cociente.

{\mathrm{log}}_{3}\left(\frac{y}{25}\right)=0

De la teoría sobre logaritmos sabemos que, sin importar la base, el logaritmo es igual a cero si el argumento es igual a 1, por tanto:

{\mathrm{log}}_{3}\left(\frac{y}{25}\right)=0\to \frac{y}{25}=1

Finalmente:

y=25

Indicamos como respuesta correcta la a).

Reactivo 5

El residuo de dividir {x}^{5}+4{x}^{4}+3{x}^{3}-{x}^{2}+3x-21 entre {x}^{3}+2{x}^{2}+1 es:

1. 2{x}^{2}+1
2. 2{x}^{2}+x-22
3. -6{x}^{2}+3x-3
4. x-22
5. x-20

Solución:

Para dividir dos polinomios podemos aplicar el algoritmo clásico, similar al empleado en aritmética para dividir números reales o el método de Ruffini. En este caso, optaremos por utilizar el primero. Recordemos que el resto de una división es la cantidad que queda del dividendo cuando no puede continuar dividiéndose de forma entera entre el divisor.

Comencemos por ordenar los polinomios.

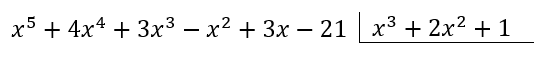
Buscamos un monomio que multiplicado por el primer término del divisor sea igual al primer término del dividendo. Hay que tener en cuenta que ambos polinomios deben estar ordenados de mayor a menor.

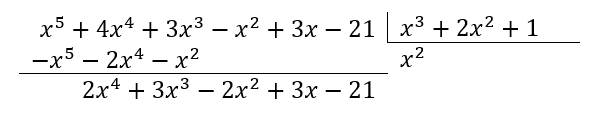
Vamos con el siguiente término.

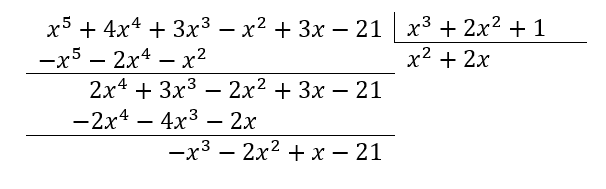
El último término antes de que el residuo sea menor que el divisor.

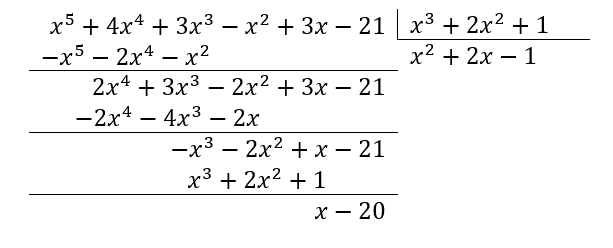
Finalmente:

\frac{{x}^{5}+4{x}^{4}+3{x}^{3}-{x}^{2}+3x-21}{{x}^{3}+2{x}^{2}+1}={x}^{2}+2x-1+\frac{x-20}{{x}^{3}+2{x}^{2}+1}

Concluimos indicando como respuesta correcta la opción e).

Reactivo 6

Las soluciones a la ecuación {x}^{2}-\mathrm{l}\mathrm{n}\left({x}^{2}+x-6\right)=2x-\mathrm{l}\mathrm{n}(x-2)+35-\mathrm{l}\mathrm{n}(x+3) son:

1. x=2,x=-3
2. x=-2,x=5
3. x=3,x=-7
4. x=1,x=6
5. x=-5,x=7

Solución:

Para calcular los valores de la ecuación, necesitamos agrupar en un mismo miembro los términos con logaritmo.

{x}^{2}-\mathrm{ln}\left({x}^{2}+x-6\right)=2x-\mathrm{ln}\left(x-2\right)+35-\mathrm{ln}\left(x+3\right)

-\mathrm{ln}\left({x}^{2}+x-6\right)+\mathrm{ln}\left(x-2\right)+\mathrm{ln}\left(x+3\right)=-{x}^{2}+2x+35

Aplicamos la propiedad del logaritmo del producto, pero en sentido inverso.

\mathrm{ln}\left(\left(x-2\right)\left(x+3\right)\right)-\mathrm{ln}\left({x}^{2}+x-6\right)=-{x}^{2}+2x+35

Ahora, la propiedad del logaritmo del cociente, también en sentido inverso.

\mathrm{ln}\left(\frac{\left(x-2\right)\left(x+3\right)}{{x}^{2}+x-6}\right)=-{x}^{2}+2x+35

Resolvemos el producto de binomios.

\mathrm{ln}\left(\frac{{x}^{2}+x-6}{{x}^{2}+x-6}\right)=-{x}^{2}+2x+35

Simplificamos.

\mathrm{ln}\left(1\right)=-{x}^{2}+2x+35\to -{x}^{2}+2x+35=0

Aplicamos la fórmula de segundo grado para obtener los valores de x que satisfacen la ecuación.

x=\frac{-2\pm \sqrt{{2}^{2}-4\left(-1\right)\left(35\right)}}{2\left(-1\right)}\to x=-5;x=7

Comparando con las opciones, seleccionamos como correcta la e).

Reactivo 7

Si x , y , z son solución del sistema de ecuaciones:

\begin{array}{c}2x+y+z=7\\ \frac{{e}^{4x}{e}^{y}}{{e}^{6}}=1\\ x+2z=12\end{array}

¿Cuál de las siguientes afirmaciones es correcta?

1. {e}^{x}{e}^{y}=1
2. {e}^{x}{e}^{z}=1
3. {e}^{y}{e}^{z}=1
4. {e}^{x}{e}^{y}{e}^{z}=1
5. {e}^{x}{e}^{y}+{e}^{z}=0

Solución:

Para comprobar cualquiera de las afirmaciones de los incisos tenemos dos opciones: modificar algebraicamente el sistema de ecuaciones hasta llegar a alguna de ellas o encontrar los valores de x , y , z y sustituirlos en cada afirmación para comprobar cuál es correcta.

El primer camino parece el más directo, pero realmente necesita de mucha manipulación y esfuerzo innecesarios. En este caso, vamos a resolver el sistema de ecuaciones.

La segunda ecuación tiene una forma peculiar de tipo exponencial, pero aplicando algunas propiedades podemos “linealizar” la ecuación.

\frac{{e}^{4x}{e}^{y}}{{e}^{6}}=1\to {e}^{4x}{e}^{y}={e}^{6}

{e}^{4x+y}={e}^{6}

Ahora, aplicando logaritmo natural en ambos miembros:

4x+y=6

Despejamos a z de la tercera ecuación y lo sustituimos en la primera.

z=\frac{12-x}{2}\to 2x+y+\frac{12-x}{2}=7

Simplificando nos queda:

3x+2y=2

Con esto, tenemos un sistema de dos ecuaciones con 2 incógnitas. Multiplicamos la primera por -2 y sumamos con la segunda.

-8x-2y=-12

3x+2y=2

-5x=-10\to x=2

Sustituimos en la primera ecuación para obtener a y .

4\left(2\right)+y=6\to y=-2

Finalmente, sustituimos en z=\frac{12-x}{2} para calcular a z .

z=\frac{12-2}{2}=5

Pasamos a comprobar las afirmaciones:

Afirmación A.

{e}^{x}{e}^{y}=1\to {e}^{2}{e}^{-2}=1

{e}^{2-2}=1\to {e}^{0}=1

\therefore 1=1

La primera afirmación es la correcta.

Concluimos seleccionando como respuesta correcta la opción a).

Reactivo 8

Se reparten 10 regalos entre Sofia, Natalia y Renata.

Sofia dice: Yo tengo el mismo número de regalos que Renata y Natalia juntas.

Natalia dice: Yo tengo la mitad de regalos que Sofía.

Renata dice: Yo tengo un regalo menos que Natalia.

Si a lo más una de ellas miente, ¿Cuál de las siguientes afirmaciones es verdadera?

1. Sofía miente
2. Natalia miente
3. Renata miente
4. Es posible que todas digan la verdad
5. No se puede saber cuántos regalos recibió cada una

Solución:

Aunque la redacción del problema complica entender lo que debemos hacer, básicamente se nos indica que la única relación entre los regalos repartidos entre Sofía, Natalia y Renata es la primera, por tanto:

S+R+N=10

Ahora, las otras tres relaciones pueden o no ser ciertas. Nuestro trabajo es armar los sistemas de 3 ecuaciones con 3 incógnitas hasta encontrar aquel que sea consistente. De las tres relaciones se extrae:

Sofia dice: Yo tengo el mismo número de regalos que Renata y Natalia juntas.

S=R+N

Natalia dice: Yo tengo la mitad de regalos que Sofía.

N=\frac{S}{2}

Renata dice: Yo tengo un regalo menos que Natalia.

R=N-1

Las ecuaciones serán 1, 2, 3 y 4 respectivamente. La 1 irá en todas las combinaciones porque es la segura, las otras dos se irán alternando. A partir de las técnicas de conteo, sabemos que solo hay 3 posibles combinaciones:

1, 2, 3

1, 2, 4

1, 3, 4

Vamos con la primera combinación:

\left\{\begin{array}{c}S+R+N=10\\ S-R-N=0\\ N=\frac{S}{2}\end{array}\right.

Sumando la primera y la segunda obtenemos el valor de S directamente.

2S=10\to S=5

Calculamos N con la tercera ecuación:

N=\frac{5}{2}=2.5

Obtenemos finalmente a R .

R=2.5

Este sistema no es el correcto, porque implica que dos hermanas comparten regalo y eso no se indica en ninguna de las relaciones.

Vamos con la segunda combinación:

\left\{\begin{array}{c}S+R+N=10\\ S-R-N=0\\ R-N=-1\end{array}\right.

Hacemos lo mismo con 1 y 2.

S=5

Sumamos 2 y 4 y sustituimos S .

S-2N=-1\to 2N=S+1

\therefore N=3

Finalmente:

R=10-S-N\to R=2

Estos resultados son enteros y consistentes. Concluimos que las afirmaciones de Sofía y Renata son correctas, por tanto, Natalia es quién miente. La opción b) es la correcta.

Reactivo 9

Un grupo de estudiantes quiere extender una cuerda desde el techo de un edificio hasta un punto P que se encuentra en el suelo a 9 m de la base del edificio. Observan que a determinada hora del día la sombra del edificio llega exactamente hasta el punto P. En ese momento, una estaca que mide 1 metro de altura proyecta una sombra de 0.75 metros.

¿Cuántos metros de cuerda tienen que comprar?

1. 6.75 metros más que lo que necesiten para amarrarla
2. 9 metros más lo que necesiten para amarrarla
3. 12 metros más lo que necesiten para amarrarla
4. 13.5 metros más lo que necesiten para amarrarla
5. 15 metros más lo que necesiten para amarrarla

Solución:

Para calcular la longitud de la cuerda que deben comprar los estudiantes, es necesario aplicar triángulos semejantes con los datos dados por el enunciado. Entre lo más alto del edificio, el punto P y la base se forma un triángulo rectángulo, al igual que entre la estaca y su sombra.

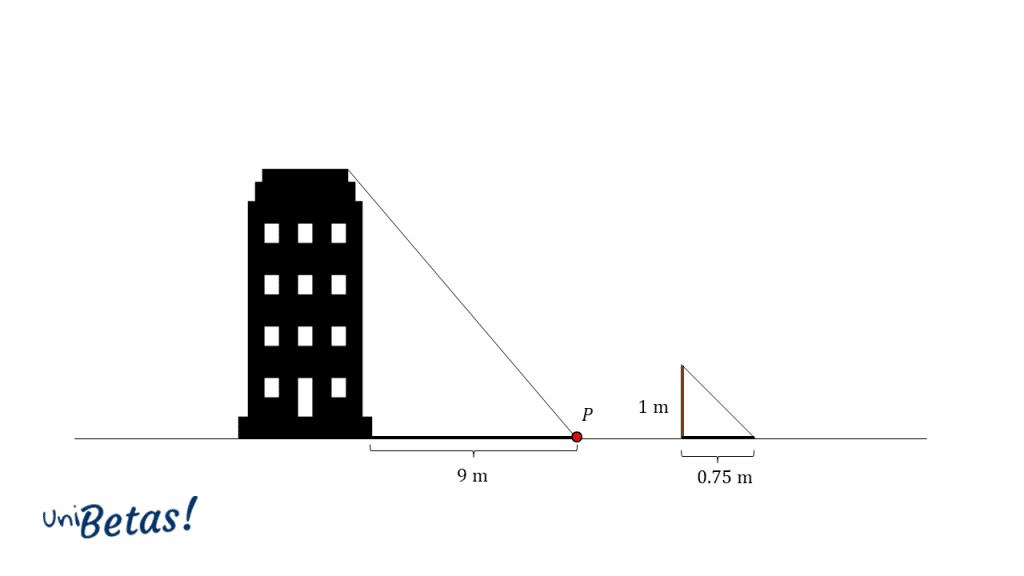
Aplicamos triángulos semejantes para obtener la altura del edificio, la cual llamaremos {h}_{e} .

\frac{{h}_{e}}{1}=\frac{9}{0.75}\to {h}_{e}=12

Ahora, empleamos el Teorema de Pitágoras para calcular la longitud de cuerda desde la punta del edificio hasta el punto P .

l=\sqrt{{12}^{2}+{9}^{2}}=15 \mathrm{m}

Teniendo en cuenta las respuestas, concluimos que los estudiantes deben comprar 15 metros de cuerda más lo necesario para amarrarla tanto arriba como abajo en el punto P . Indicamos como correcta la opcion e).

Reactivo 10

¿Cuál es la distancia de un vértice al centro de un cubo de lado 2?

1. \sqrt{2}
2. \sqrt{3}
3. \frac{1}{\sqrt{2}}
4. \frac{1}{\sqrt{3}}
5. 2\sqrt{3}

Solución:

 

Este problema puede resolverse recurriendo a distintos enfoques geométricos, en este caso vamos considerar que tomamos uno de los vértices del cubo y lo colocamos en el origen de un sistema de coordenadas en el espacio, tal como se muestra a continuación.

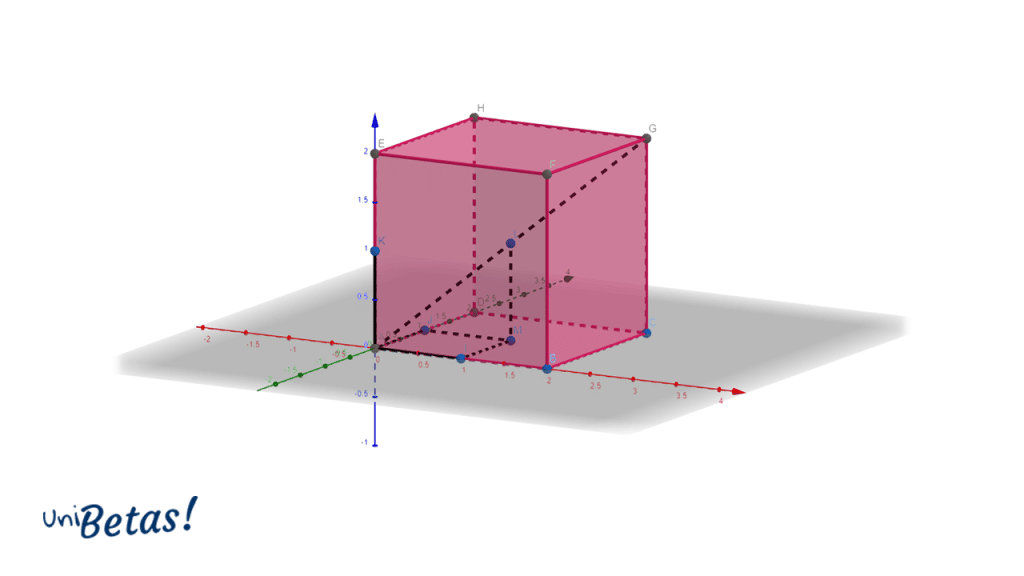
En dicha imagen, también se traza un segmento entre dos vértices opuestos y sobre dicha diagonal del cubo, se ubica el centro, el cual se encuentra en el punto \left(1, 1, 1\right) , es decir, en la mitad de cada una de las aristas del cubo.

La distancia entre cualquiera de los 4 vértices y el punto central del cubo se puede calcular aplicando la fórmula de distancia entre dos puntos en el plano.

d\left({P}_{1}, {P}_{2}\right)=\sqrt{{\left({x}_{1}-{x}_{2}\right)}^{2}+{\left({y}_{1}-{y}_{2}\right)}^{2}+{\left({z}_{1}-{z}_{2}\right)}^{2}}

Nuestro punto 1 será el origen de coordenadas {P}_{1}\left(0, 0, 0\right) y el punto 2 el centro del cubo {P}_{2}\left(1, 1, 1\right) .

d\left({P}_{1}, {P}_{2}\right)=\sqrt{{\left(0-1\right)}^{2}+{\left(0-1\right)}^{2}+{\left(0-1\right)}^{2}}

d\left({P}_{1},{P}_{2}\right)=\sqrt{3}

Concluimos seleccionando como respuesta correcta la opción b).

Reactivo 11

Tenemos que \mathrm{t}\mathrm{a}\mathrm{n}\left(\alpha \right)=\frac{3}{4} . ¿Cuánto vale \mathrm{cos}\left(\alpha \right) ?

1. \frac{3}{5}
2. \frac{4}{5}
3. \frac{4}{3}
4. 4
5. \frac{1}{4}

Solución:

Para calcular el valor del coseno sin utilizar la inversa de la tangente, debemos recurrir a las identidades trigonométricas fundamentales. Comencemos por armar un triángulo rectángulo a partir de los valores dados para la tangente.

\mathrm{tan}\left(\alpha \right)=\frac{3}{4}=\frac{\mathrm{C}\mathrm{O}}{\mathrm{C}\mathrm{A}}

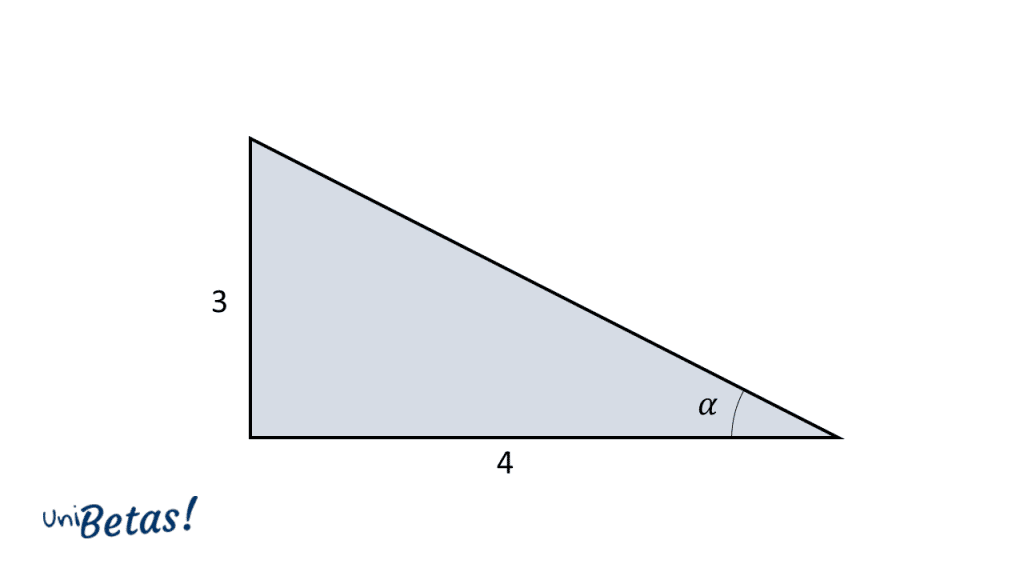
Calculamos la hipotenusa del triángulo rectángulo.

h=\sqrt{{4}^{2}+{3}^{2}}=5

Ya que el coseno del ángulo es igual al cateto adyacente sobre la hipotenusa, concluimos:

\mathrm{cos}\left(\alpha \right)=\frac{4}{5}

Comparando con las opciones, indicamos como correcta la b).

Reactivo 12

Calcula \underset{h\to 0}{lim} \frac{\sqrt{x+h}-\sqrt{x}}{h} y exprésalo en función de x .

1. 0
2. \frac{1}{2\sqrt{x}}
3. 2\sqrt{x}
4. \frac{-1}{2\sqrt{2}}
5. -2\sqrt{x}

Solución:

Iniciamos evaluando el límite:

\underset{h\to 0}{lim} \frac{\sqrt{x+h}-\sqrt{x}}{h}=\frac{\sqrt{x+0}-\sqrt{x}}{0}=\frac{0}{0}

Tenemos que deshacernos de la indeterminación. Comenzamos por multiplicar y dividir por el conjugado del numerador.

\underset{h\to 0}{lim} \frac{\sqrt{x+h}-\sqrt{x}}{h}\bullet \frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}}=\underset{h\to 0}{lim} \frac{x+h-x}{h\left(\sqrt{x+h}+\sqrt{x}\right)}

Simplificamos.

\underset{h\to 0}{lim} \frac{h}{h\left(\sqrt{x+h}+\sqrt{x}\right)}=\underset{h\to 0}{lim} \frac{1}{\sqrt{x+h}+\sqrt{x}}

Evaluamos nuevamente el límite.

\underset{h\to 0}{lim} \frac{1}{\sqrt{x+h}+\sqrt{x}}=\frac{1}{\sqrt{x+0}+\sqrt{x}}=\frac{1}{2\sqrt{x}}

Concluimos entonces que:

\underset{h\to 0}{lim} \frac{\sqrt{x+h}-\sqrt{x}}{h}=\frac{1}{2\sqrt{x}}

Escogemos como correcta la opción b).

Reactivo 13

La derivada de la función {\mathrm{s}\mathrm{e}\mathrm{c}}^{4}\left(2{x}^{2}\right) es:

1. 16x\cdot {\mathrm{s}\mathrm{e}\mathrm{c}}^{3}\left(2{x}^{2}\right)\cdot \mathrm{t}\mathrm{a}\mathrm{n}\left(2{x}^{2}\right)
2. 4x\cdot {\mathrm{s}\mathrm{e}\mathrm{c}}^{4}\left(2{x}^{2}\right)\cdot \mathrm{t}\mathrm{a}\mathrm{n}\left(2{x}^{2}\right)
3. 4{\mathrm{s}\mathrm{e}\mathrm{c}}^{3}\left(2{x}^{2}\right)\cdot \mathrm{t}\mathrm{a}\mathrm{n}\left(2{x}^{2}\right)
4. 4x\cdot {\mathrm{s}\mathrm{e}\mathrm{c}}^{3}\left(2{x}^{2}\right)\cdot \mathrm{t}\mathrm{a}\mathrm{n}\left(2{x}^{2}\right)
5. 16x\cdot {\mathrm{s}\mathrm{e}\mathrm{c}}^{4}\left(2{x}^{2}\right)\cdot \mathrm{t}\mathrm{a}\mathrm{n}\left(2{x}^{2}\right)

Solución:

Para calcular la derivada de esta función, debemos aplicar la regla de la cadena. Es necesario identificar la función principal, en este caso, dicha función es la de la cuarta potencia. Aplicamos la fórmula de la derivada de una potencia:

{y}^{\text{'}}=4{\mathrm{sec}}^{3}\left(2x\right){\left[\mathrm{sec}\left(2{x}^{2}\right)\right]}^{\text{'}}

Queda indicada la derivada de la secante, cuyo resultado es:

{y}^{\text{'}}=4{\mathrm{sec}}^{3}\left(2{x}^{2}\right){\left[\mathrm{sec}\left(2{x}^{2}\right)\right]}^{\text{'}}=4{\mathrm{sec}}^{3}\left(2{x}^{2}\right)\mathrm{tan}\left(2{x}^{2}\right)\mathrm{sec}\left(2{x}^{2}\right){\left(2{x}^{2}\right)}^{\text{'}}

Debido a que el argumento de la secante es también otra función, esta queda indicada al derivar. Finalmente:

{y}^{\text{'}}=4{\mathrm{sec}}^{3}\left(2{x}^{2}\right)\mathrm{tan}\left(2{x}^{2}\right)\mathrm{sec}\left(2{x}^{2}\right)4x=16x{\mathrm{sec}}^{4}\left(2{x}^{2}\right)\mathrm{tan}\left(2{x}^{2}\right)

{y}^{\text{'}}=16x{\mathrm{sec}}^{4}\left(2{x}^{2}\right)\mathrm{tan}\left(2{x}^{2}\right)

Concluimos el ejercicio seleccionando como correcta la opción e).

Reactivo 14

El resultado de evaluar la integral {\int }_{0}^{1} x{e}^{{x}^{2}}dx es:

1. \frac{e-1}{2}
2. \frac{e+1}{2}
3. \frac{1-e}{2}
4. \frac{2}{e-1}
5. \frac{2}{1-e}

Solución:

En este caso, debemos encontrar la primitiva de la función integrando y luego aplicar el segundo teorema fundamental del cálculo que dice:

Si F\left(x\right) es una primitiva de la función f\left(x\right) y ambas funciones son continuas en el intervalo cerrado \left[a, b\right] , el valor de la integral de f\left(x\right) en dicho intervalo se calcula como:

{\int }_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)

Integramos indefinidamente y luego evaluamos en los extremos. Esta integral sale por cambio de variable:

v={x}^{2}\to dv=2xdx

\therefore \frac{1}{2}dv=xdx

Sustituimos:

\frac{1}{2}{\int }_{{v}_{a}}^{{v}_{b}} {e}^{v}dv

Esta integral es inmediata.

\frac{1}{2}{\int }_{{v}_{a}}^{{v}_{b}} {e}^{v}dv=\frac{1}{2}{e}^{v}|\begin{array}{c}{v}_{b}\\ {v}_{a}\end{array}

Devolvemos el cambio de variables.

i=\frac{1}{2}{e}^{{x}^{2}}|\begin{array}{c}1\\ 0\end{array}=\frac{1}{2}\left({e}^{1}-1\right)=\frac{e-1}{2}

Finalmente:

{\int }_{0}^{1} x{e}^{{x}^{2}}dx=\frac{e-1}{2}

Indicamos como respuesta correcta la opción a).