Guía UNAM Física: Área 2 Cs Biológicas Químicas y de la Salud

Temas	Área 2
Español	18
Matemáticas	24
Física	12
Química	13
Biología	13
Historia universal	10
Historia de México	10
Literatura	10
Geografía	10
Filosofía	NA
Total	120

¿Sabías que hay carreras con requisitos adicionales a la prueba de ingreso? Fisioterapia y ciencias forenses son 2 de las 9 carreras de área 2 con ingreso indirecto.

¿Cómo estudiar física para el examen?

Física es una de las ciencias exactas más apasionantes y complejas que existen y, debido a esto último, puede llegar a ser frustrante en muchos casos.

No se trata de solo despejar ecuaciones y encontrar valores, trata de observar la naturaleza, entenderla, describirla y cuantificarla mediante modelos matemáticos para explorar en aquellos rincones donde nuestros sentidos pierden efecto.

Los siguientes consejos te permitirán ver a la física desde otra perspectiva.

Guía física UNAM área 2 resuelta

Comenzamos con la solución paso a paso de los 12 reactivos de física, para la guía UNAM del área 2 Ciencias Biológicas, Químicas y de la Salud.

Reactivo 1

¿Qué representa la siguiente gráfica?

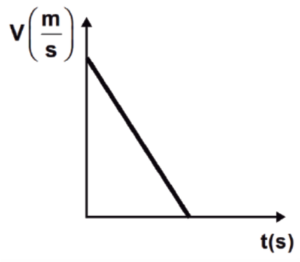
1. La caída libre de un cuerpo desde el reposo.
2. Un lanzamiento vertical hacia abajo.
3. Un movimiento con aceleración positiva.
4. Un movimiento con aceleración negativa.

Solución:

En la gráfica del enunciado, se observa como la velocidad disminuye en línea recta hasta hacerse cero respecto del tiempo. Esto solo ocurre cuando la aceleración del cuerpo que experimenta el movimiento es negativa. Esto nos deja dos opciones: el inciso A o el inciso D.

En caída libre los cuerpos experimentan una aceleración negativa, pero solo con la gráfica de la velocidad no podemos concluir que se trate de una caída libre. Puede ser cualquier otro movimiento desacelerado como un coche frenando.

Teniendo en cuenta todo el análisis, se concluye que la respuesta correcta es el inciso D.

Reactivo 2

Tres caballos jalando una carreta de 500 kg en la misma dirección. Cada uno de los caballos ejerce una fuerza de 1 500 N sobre la carreta. Si no hay fricción entre la carreta y el suelo, la fuerza total con la que ésta es jalada es de:

1. 3 N
2. 300 N
3. 1,500 N
4. 4,500 N

Solución:

En este caso, debemos encontrar la fuerza total aplicada sobre la carreta que ejercen los 3 caballos. Con ayuda del siguiente diagrama, podemos darnos cuenta que las tres fuerzas se aplican en la misma dirección y poseen el mismo sentido.

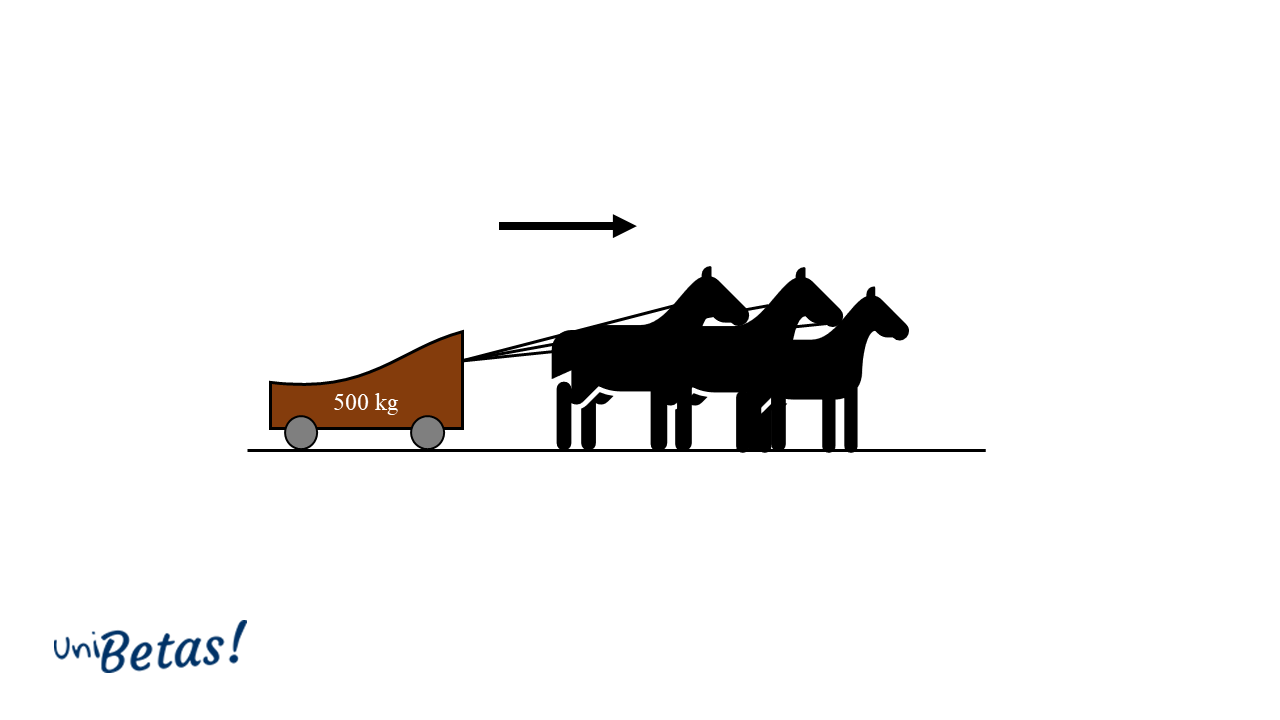
La fuerza total experimentada por la carrera es la suma de las fuerzas individuales de los caballos.

{F}_{t}={F}_{1}+{F}_{2}+{F}_{3}

Podemos permitirnos trabajar notación vectorial, debido a que todas las fuerzas actúan en la misma dirección. Sustituimos y calculamos.

F=\mathrm{1,500} \mathrm{N}+\mathrm{1,500} \mathrm{N}+\mathrm{1,500} \mathrm{N}=\mathrm{4,500}\mathrm{ }\mathrm{N}

Los tres caballos ejercen una fuerza total de 4500 Newtons sobre la carreta.

Comparando con las opciones, la respuesta correcta se encuentra en el inciso D.

Reactivo 3

Una báscula tiene un resorte cuya constante de elasticidad es de 1000\frac{\mathrm{N}}{\mathrm{m}} , al colocar en ésta una masa de 10 kg, ¿cuánto se estirará su resorte? Considera g=10\frac{\mathrm{m}}{{\mathrm{s}}^{2}} .

1. 0.10 \mathrm{m}
2. 1.0 \mathrm{m}
3. 0.01 \mathrm{m}
4. 10.0 \mathrm{m}

Solución:

Realizamos una representación gráfica de la situación planteada.

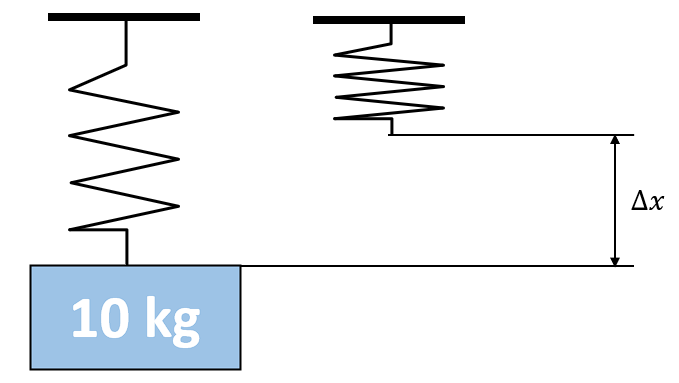
El peso de la masa presiona hacia abajo al resorte, mientras que la fuerza elástica con la misma magnitud, pero con signo contrario se opone a continuar deformando el resorte. Aplicando la primera ley de Newton nos queda:

{F}_{e}-mg=0

Se utiliza la Ley de Hooke para sustituir la fuerza elástica.

{F}_{e}=k\mathrm{\Delta }x

k\mathrm{\Delta }x-mg=0

Despejamos la deformación:

\mathrm{\Delta }x=\frac{mg}{k}

Sustituimos:

\mathrm{\Delta }x=\frac{\left(10\right)\left(10\right)}{1000}=0.1\mathrm{ }\mathrm{m}

El resorte se deforma 0.1 metros. La respuesta correcta es el inciso A.

Reactivo 4

Una bola de billar se sube a 3 m de altura en diferentes casos, como muestran las figuras. Indica cuál de las afirmaciones que se presentan es correcta.

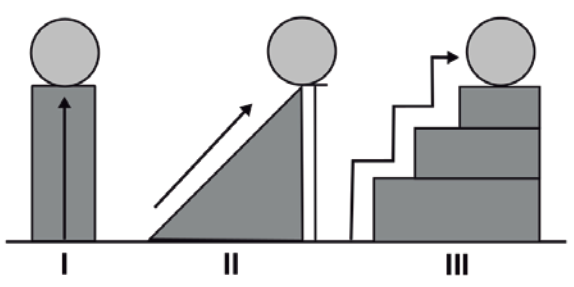
1. En el caso I se efectúa mayor trabajo.
2. En el caso II se efectúa menor trabajo.
3. En el caso I y III se efectúa menos trabajo que en el II.
4. En los tres casos se efectúa igual trabajo.

Solución:

El trabajo que aplica una fuerza sobre un cuerpo se calcula como el producto escalar entre la fuerza y el vector desplazamiento que experimenta el cuerpo.

W=\overrightarrow{F}\cdot \overrightarrow{d}=F\cdot d\mathrm{cos}\theta 

El producto escalar hace que la fuerza aplicada se proyecte sobre el vector desplazamiento, asegurando que el trabajo final sea efectuado por la componente de la fuerza que apunta en la dirección del desplazamiento.

Teniendo en cuenta lo anterior, en las tres figuras la altura final es igual a 3 metros y el objetivo es llevar a la masa desde el suelo hacia la cima.

Aunque la primera tenga un camino directo hacia arriba, la segunda sea una rampa y la tercera una escalera, el trabajo en las tres para subir la masa es el mismo. Tal vez la fuerza sea distinta en las tres situaciones, pero la componente de \overrightarrow{F} necesaria para subir la masa tiene el mismo valor en las tres.

Se concluye indicando como respuesta correcta al inciso D.

Reactivo 5

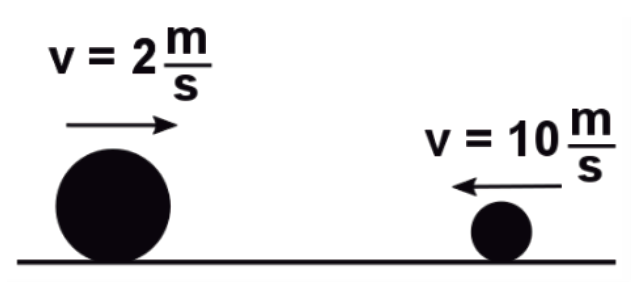
Una pelota de 2 kg se desplaza hacia la izquierda con una velocidad de 10 m/s, y choca de frente con una pelota de 4 kg que viaja hacia la derecha a 2 m/s. Calcula la velocidad final si las dos pelotas se quedan pegadas después del choque.

1. 5\frac{\mathrm{m}}{\mathrm{s}}
2. -8\frac{\mathrm{m}}{\mathrm{s}}
3. 12\frac{\mathrm{m}}{\mathrm{s}}
4. -2\frac{\mathrm{m}}{\mathrm{s}}

Solución:

El tipo de choque descrito por el enunciado, debido a que las masas permanecen pegadas luego de la colisión y se disipa toda la energía cinética, se denomina perfectamente inelástico. Para resolver el problema, aplicamos el principio de conservación del momento lineal.

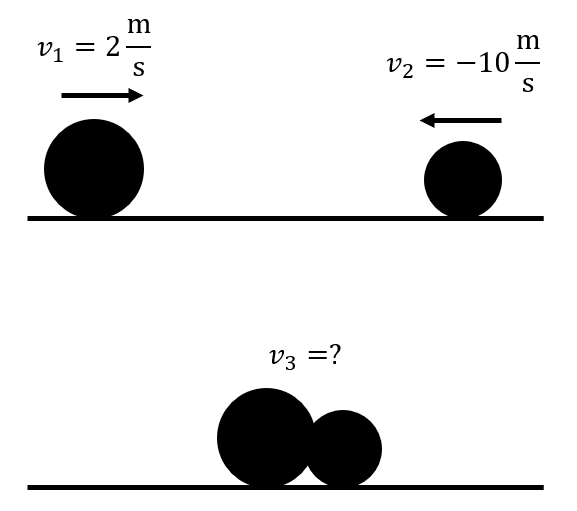
{m}_{1}{v}_{1}-{m}_{2}{v}_{2}=\left({m}_{1}+{m}_{2}\right){v}_{3}

Despejamos la velocidad final {v}_{3} .

{v}_{3}=\frac{{m}_{1}{v}_{1}-{m}_{2}{v}_{2}}{{m}_{1}+{m}_{2}}

Sustituimos.

{v}_{3}=\frac{\left(2\right)\left(4\right)-\left(10\right)\left(2\right)}{2+4}=\frac{8-20}{6}=-\frac{12}{6}=-2\frac{\mathrm{m}}{\mathrm{s}}

La velocidad final de las masas luego del choque es igual a -2\frac{\mathrm{m}}{\mathrm{s}} . La respuesta correcta es el inciso D.

Reactivo 6

¿Cuál es la densidad del oxígeno diatómico que está a una temperatura de 27°C y a una atmósfera de presión? Considera: La masa molecular del oxígeno monoatómico es 16 uma.

El valor de la constante universal del gas ideal es de 8.314\frac{\mathrm{J}}{\mathrm{m}\mathrm{o}\mathrm{l}\cdot \mathrm{K}} .

1. 0.08\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}
2. 14.4\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}
3. 0.6\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}
4. 1.3\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}

Solución:

La masa molecular del oxígeno monoatómico 16 UMA es equivalente a 16\frac{\mathrm{g}}{\mathrm{m}\mathrm{o}\mathrm{l}} . Por lo tanto, para el oxígeno diatómico será el doble: 32\frac{\mathrm{g}}{\mathrm{m}\mathrm{o}\mathrm{l}} , expresado en \frac{\mathrm{k}\mathrm{g}}{\mathrm{m}\mathrm{o}\mathrm{l}} nos queda:

M=0.032\frac{\mathrm{k}\mathrm{g}}{\mathrm{m}\mathrm{o}\mathrm{l}}

Empleamos la siguiente ecuación para calcular la densidad del gas ideal.

\rho =\frac{PM}{RT}

Se sustituye la temperatura en Kelvin y la presión en Pascales.

1 \mathrm{a}\mathrm{t}\mathrm{m}\to 101325 \mathrm{P}\mathrm{a}

T=273+27=300 \mathrm{K}

\rho =\frac{\left(101325\right)\left(0.032\frac{\mathrm{k}\mathrm{g}}{\mathrm{m}\mathrm{o}\mathrm{l}}\right)}{\left(8.314\right)\left(300\right)}=1.3\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}

La densidad del oxígeno diatómico es igual a 1.3\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}} .

La respuesta correcta es el inciso D.

Reactivo 7

A la playa llega el oleaje del mar y en ocasiones llegan algunas olas de mayor tamaño que el promedio. Lo anterior se debe al comportamiento ondulatorio de las olas, pues una característica de éstas es que se:

1. refractan.
2. polarizan.
3. reflejan.
4. superponen.

Solución:

Una propiedad fundamental de los fenómenos ondulatorios, es que matemáticamente se pueden describir a partir de modelos lineales. Esto tiene una implicación importante en el análisis de ondulaciones, porque los fenómenos lineales cumplen la propiedad de superposición.

Cuando dos o más ondas que se propagan por un medio se encuentran en un punto, la onda resultante se obtiene como la suma algebraica de las ondulaciones originales.

Teniendo en cuenta lo anterior, cuando las crestas de las olas del mar se encuentran en determinado punto, el resultado será otra ola con una cresta de mayor tamaño. Concluimos indicando como respuesta correcta al inciso D.

Reactivo 8

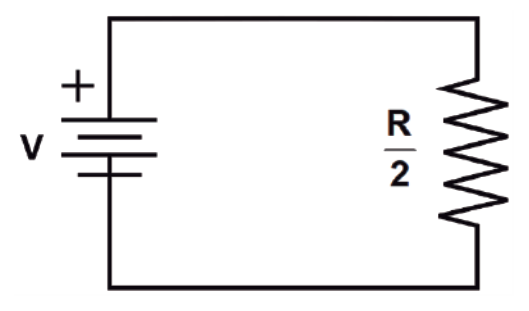
De acuerdo con la imagen, la corriente que circula por el resistor de resistencia R/2 es:

1. \frac{V}{2R}
2. \frac{2V}{R}
3. \frac{V}{3R}
4. \frac{3V}{R}

Solución:

La corriente que circula por una resistencia se calcula aplicando la ley de Ohm:

I=\frac{V}{R}

Donde V es la diferencia de potencial en terminales del resistor. Debido a que \frac{R}{2} está conectada en paralelo a la fuente, su diferencia de potencial es la misma que la de la fuente: V . Sustituimos todo en la ley de Ohm:

I=\frac{V}{\frac{R}{2}}=\frac{2V}{R}

La respuesta correcta es el inciso B.

Reactivo 9

El orden creciente de la longitud de onda para el color azul (z), el verde (v), el rojo (r), y la luz amarilla (a) es:

1. r, a, v, z.
2. a, v, r, z.
3. v, a, z, r.
4. z, v, a, r.

Solución:

Para responder esta pregunta, necesitas conocer previamente el valor de la longitud de onda de los colores del arcoíris.

Longitud de onda de los colores mencionados en el enunciado. El valor indicado corresponde al extremo superior del rango para cada color.

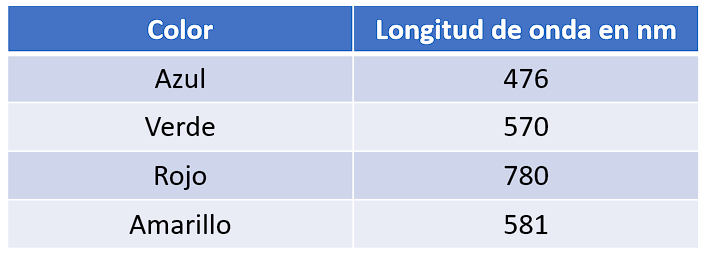
Ordenando de forma ascendente nos queda: z, v, a, r.

Concluimos indicando como respuesta correcta al inciso D.

Reactivo 10

La presión atmosférica en el Everest disminuye comparada con la del nivel del mar porque:

1. la densidad del aire cambia.
2. la altura de la capa de aire soportada es menor.
3. la presión hidrostática del mar influye.
4. la densidad del aire soportada es mayor.

Solución:

La presión atmosférica es consecuencia de la fuerza que ejerce la columna de partículas que se encuentran en la atmósfera terrestre sobre la superficie de la tierra. Lo anterior implica que: a medida que subimos, la columna de partículas es menor y, por ende, la presión también es menor.

A partir del análisis anterior, concluimos que la respuesta correcta es el inciso B.

Reactivo 11

¿Qué tipo de imagen forma un espejo convexo?

1. Virtual, derecha y menor que el objeto.
2. Virtual, invertida y mayor que el objeto.
3. Real, invertida y menor que el objeto.
4. Virtual, derecha y mayor que el objeto.

Solución:

Los espejos convexos son aquellos cuya curvatura es externa. En este caso, cualquiera que sea la posición del objeto frente al espejo, la imagen será virtual, derecha y reducida de tamaño.

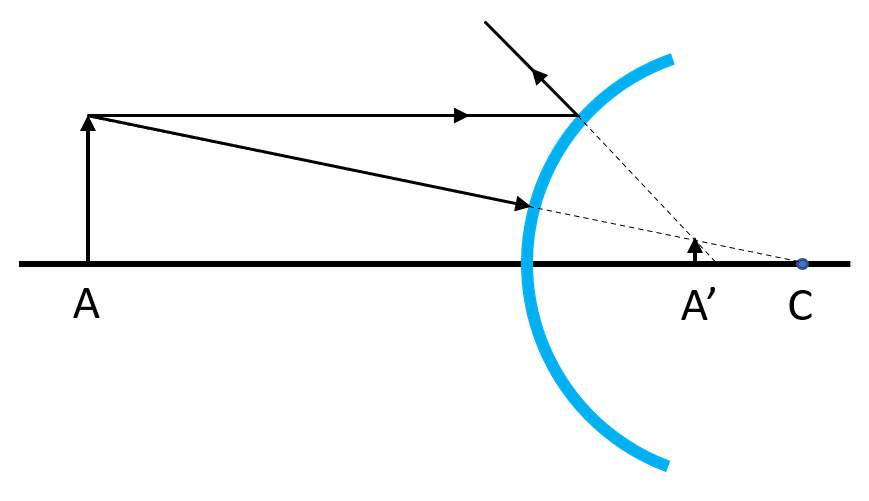
La respuesta correcta es el inciso A.

Reactivo 12

¿Cuál de las siguientes opciones es un postulado del modelo atómico de Bohr?

1. Los electrones en órbita circular cuando están acelerados pierden energía y caen al núcleo.
2. Los electrones se mueven en estados estacionarios alrededor del núcleo sin perder energía.
3. De acuerdo con la radiación beta debe haber electrones en el núcleo atómico.
4. Un electrón en el átomo puede variar continuamente el valor de su energía.

Solución:

Es uno de los modelos atómicos propuestos antes de la descripción exacta de las interacciones atómicas a través de la mecánica cuántica.

El modelo de Bohr establece 3 postulados y, entre ellos, se introduce el concepto de cuantización de la energía y otros aspectos similares al modelo atómico actual. A continuación, los tres postulados del modelo:

1. Los electrones se mueven en trayectorias circulares sin emitir energía.
2. Las órbitas permitidas son aquellas con momento angular múltiplo de la constante reducida de Planck.
3. Los electrones emiten o absorben energía al desplazarse entre órbitas en forma de un fotón, cuya energía de emisión es la diferencia entre la energía de los niveles.

Teniendo en cuenta los 3 postulados descritos, concluimos que la respuesta correcta es la opción B.

Temario física área 2

El temario de física para el área 2 de Ciencias Biológicas, Químicas y de la Salud UNAM puede parecer extenso, pero si organizas tu tiempo podrás cubrirlos todos.