¡Felicidades aspirante! Vamos con la solución de la tercera y última parte del simulador real de matemáticas, diseñado especialmente para el examen de ingreso a la UNAM.

¡No pares y sigue aprendiendo! Continúa estudiando con el resto de material gratuito que tenemos en Unibetas para ti.
Simulador de Matemáticas UNAM
Vamos con los últimos 10 ejercicios (reactivos del 41 al 50) en el simulador real de matemáticas para la UNAM.
Reactivo 41
Obtenga la ecuación general de la circunferencia de radio 1 y centro en \left(1, 1\right) .
- {x}^{2}+{y}^{2}+2x-2y+1=0
- {x}^{2}+{y}^{2}-2x-2y+1=0
- {x}^{2}+{y}^{2}-2x+2y+1=0
- {x}^{2}+{y}^{2}+2x+2y+1=0
Solución:
Partimos de la ecuación ordinaria de la circunferencia.
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
Sustituimos los valores de radio y centro.
{\left(x-1\right)}^{2}+{\left(y-1\right)}^{2}=1
Desarrollamos para llegar a la forma general.
{x}^{2}-2x+1+{y}^{2}-2y+1=1
Simplificamos.
{x}^{2}+{y}^{2}-2x-2y+1=0
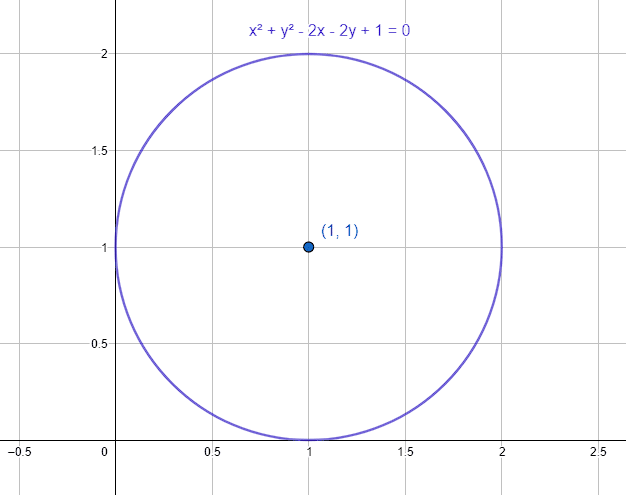
La respuesta correcta es el inciso b).
Reactivo 42
Identifique cada uno de los elementos señalados en la siguiente circunferencia.
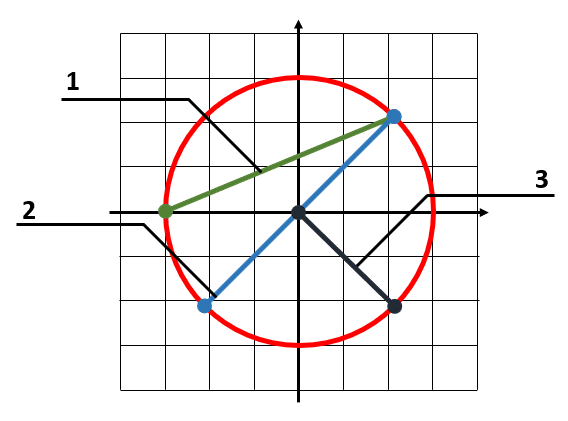
- Diámetro – diámetro – radio
- Sagita – diámetro – radio
- Cuerda – diámetro – radio
- Cuerda – radio – diámetro
Solución:
Vamos a identificar, una a una, las partes señaladas en la figura, para luego seleccionar la respuesta correcta.
El primer elemento señalado corresponde a un segmento de recta entre dos puntos de la circunferencia que mide menos que el diámetro. Este elemento corresponde a una cuerda en la circunferencia.
El segundo elemento se identifica a simple vista, y corresponde al diámetro de la circunferencia. Finalmente, el tercer elemento es el radio de la circunferencia. Teniendo en cuenta el orden señalado, los elementos son:
Cuerda – diámetro – radio
Seleccionamos como respuesta correcta al inciso c).
Reactivo 43
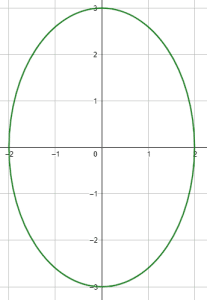
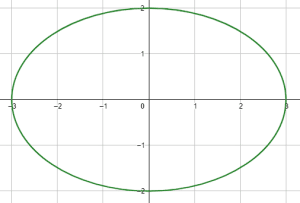
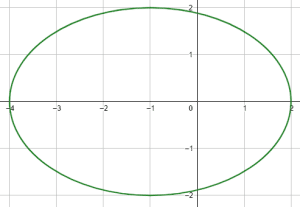
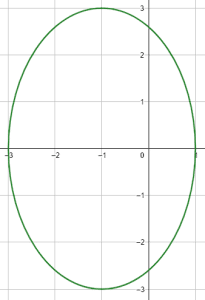
¿Cuál de las siguientes imágenes corresponde a la gráfica de la elipse \frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}=1 ?
Solución:
Examinando la ecuación de la elipse que indica el enunciado, sabemos que la misma tiene como centro el punto \left(0, 0\right) , por tanto, podemos descartar a las opciones c) y d).
De la ecuación, sabemos que el semieje mayor mide a=3 y el menor b=2 . Ya que el semieje mayor se encuentra debajo de la y , concluimos que se trata de una elipse centrada en el origen y orientada verticalmente.
La respuesta correcta es el inciso a).
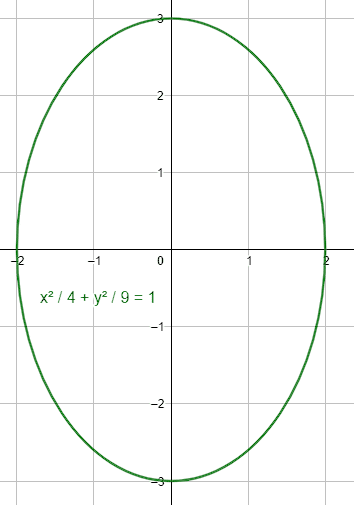
Reactivo 44
Obtenga las coordenadas de los focos de la elipse horizontal, centrada en el punto \left(1, 0\right) y cuyos semiejes miden 4 y 5 unidades.
- {f}_{1}=\left(0, -2\right), {f}_{2}=\left(0, 4\right)
- {f}_{1}=\left(-2, 0\right), {f}_{2}=\left(4, 0\right)
- {f}_{1}=\left(2, 0\right), {f}_{2}=\left(-4, 0\right)
- {f}_{1}=\left(2, 0\right), {f}_{2}=\left(4, 0\right)
Solución:
Las coordenadas de los focos de la elipse horizontal, las podemos calcular como:
{f}_{\mathrm{1,2}}=\left(h\pm c, k\right)
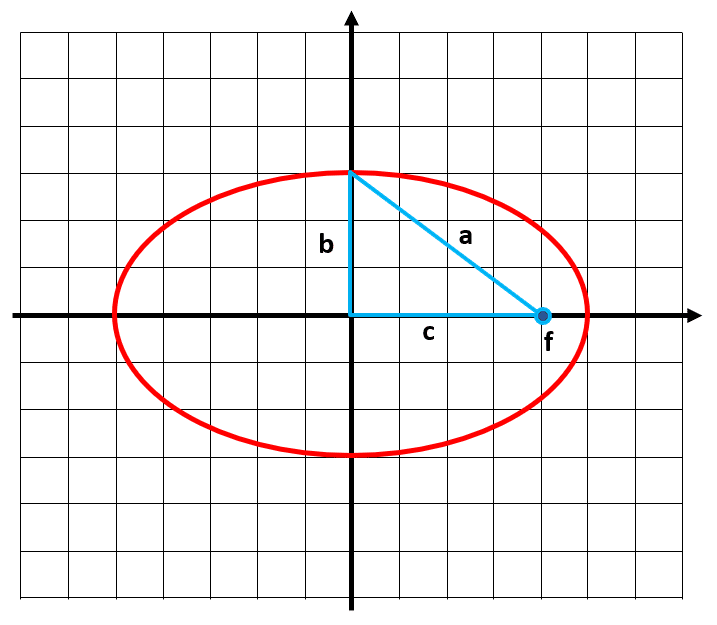
Donde c es la semidistancia entre los focos de la elipse, y la podemos calcular como:
c=\sqrt{{a}^{2}-{b}^{2}}
Sustituimos en la ecuación:
c=\sqrt{{5}^{2}-{4}^{2}}=3
Las coordenadas de los focos serían:
{f}_{1}=\left(-2, 0\right), {f}_{2}=\left(4, 0\right)
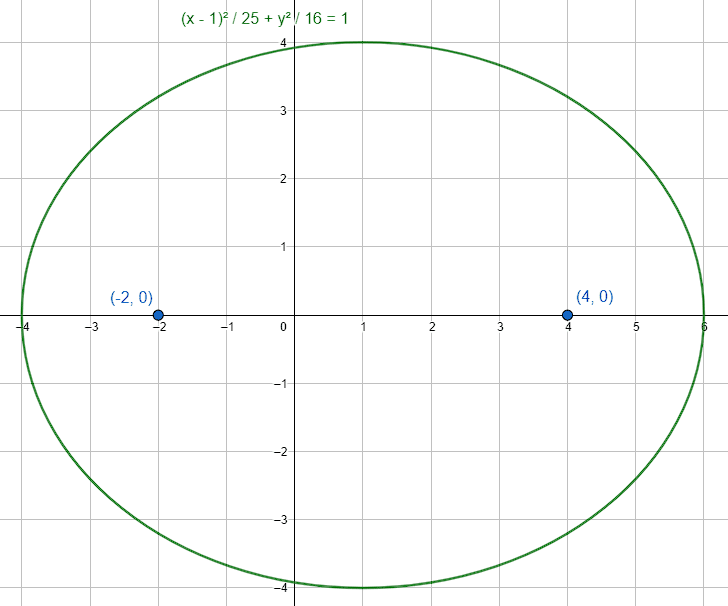
La respuesta correcta es el inciso b).
Otros aspirantes también leyeron:
- ¿Ya sabes cómo aplicar a la UNAM? Todo sobre la convocatoria UNAM pasos de registro
- Conoce la estructura completa del examen: Guía UNAM
- Lista de carreras: Oferta académica de la UNAM
- Conoce los aciertos que necesitas: Lista completa de puntajes mínimos
Reactivo 45
¿Cuál de las siguientes aseveraciones es una forma correcta de obtener una circunferencia a partir de una elipse?
- Cuando los focos de la elipse tocan su lugar geométrico, esta se convierte en una circunferencia
- Cuando la distancia entre los focos es nula, la elipse se convierte en una circunferencia
- Cuando el centro va fuera del origen
- Cuando el eje mayor es la mitad del eje menor
Solución:
Sabemos que la principal diferencia entre una elipse y una circunferencia, es que una tiene dos “radios” (eje mayor y eje menor) y la otra tiene solo uno. Por esta razón, la diferencia en sus geometrías.

Ahora, la elipse tiene otro parámetro, la semi distancia focal c y se calcula como:
c=\sqrt{{a}^{2}-{b}^{2}}
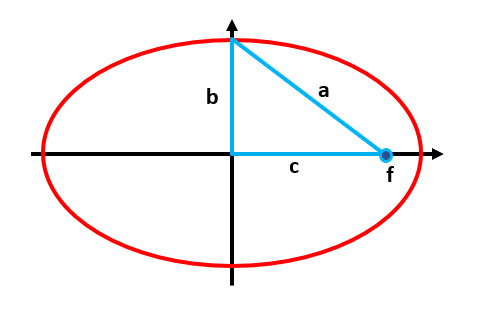
En la imagen podemos observar que: a medida que c se hace más pequeño, el valor de b se acerca al de a . Se c lleva a valer 0, a=b y, por tanto, la elipse se convertiría en una circunferencia.
{c}^{2}+{b}^{2}={a}^{2}\to c=0
\therefore b=a
Teniendo esto en cuenta y considerando los incisos, concluimos que la respuesta correcta es el b).
Reactivo 46
Calcule las coordenadas de los focos para la elipse \frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1 .
- {f}_{1}=\left(0, -5\right) y {f}_{2}=\left(0, 5\right)
- {f}_{1}=\left(-5, 0\right) y {f}_{2}=\left(5, 0\right)
- {f}_{1}=\left(-5, 1\right) y {f}_{2}=\left(5, -1\right)
- {f}_{1}=\left(0, 0\right) y {f}_{2}=\left(5, 0\right)
Solución:
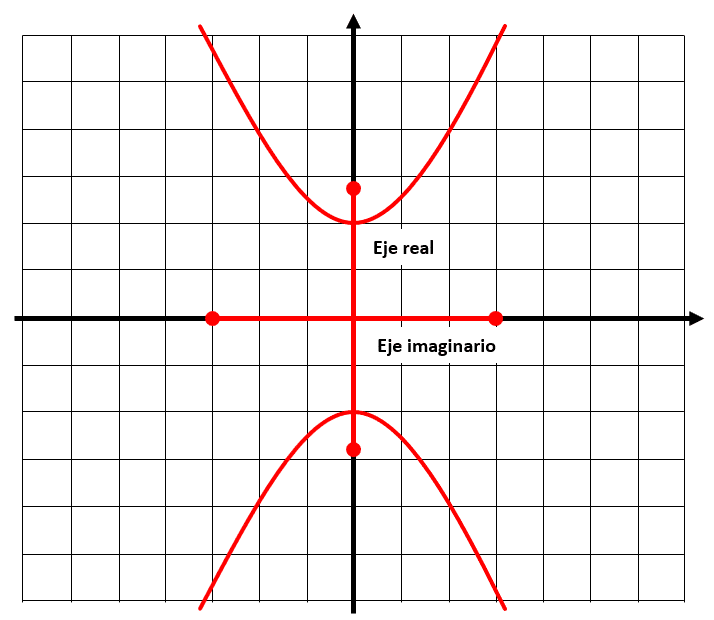
Primero debemos identificar la dirección de la hipérbola: horizontal o vertical. Debido a que la x es quien se encuentra a la izquierda del signo negativo, es una hipérbola horizontal.
Definido esto, las coordenadas de los focos serán:
{f}_{\mathrm{1,2}}=\left(h\pm c, k\right)
Donde h,k son las coordenadas del centro. La hipérbola está centrada en el origen, por tanto:
{f}_{\mathrm{1,2}}=\left(\pm c, 0\right)
Al igual que en la elipse, el parámetro c es la semidistancia focal y se calcula como:
c=\sqrt{{a}^{2}+{b}^{2}}
Los valores de {a}^{2} y {b}^{2} se extraen directamente de la ecuación.
c=\sqrt{16+9}=\sqrt{25}=5
Finalmente, los focos de la hipérbola son:
{f}_{1}=\left(-5, 0\right) y {f}_{2}=\left(5, 0\right)
La respuesta correcta es la opción b).
Reactivo 47
Encuentre la ecuación ordinaria de la hipérbola vertical, con centro en \left(2, 0\right) , que pasa por el punto \left(4, 1\right) y con semieje imaginario b=4 .
- \frac{5{y}^{2}}{4}-\frac{{\left(x+2\right)}^{2}}{16}=1
- \frac{{y}^{2}}{4}-\frac{{\left(x-2\right)}^{2}}{16}=1
- \frac{5{y}^{2}}{4}-\frac{{\left(x-2\right)}^{2}}{16}=1
- \frac{5{y}^{2}}{4}-\frac{{\left(x+2\right)}^{2}}{16}=1
Solución:
Ya que el enunciado nos dice que la hipérbola es vertical, su ecuación ordinaria es:
\frac{{\left(y-k\right)}^{2}}{{a}^{2}}-\frac{{\left(x-h\right)}^{2}}{{b}^{2}}=1
Sustituimos el centro y el semieje real.
\frac{{\left(y-0\right)}^{2}}{{a}^{2}}-\frac{{\left(x-2\right)}^{2}}{{4}^{2}}=1\to \frac{{y}^{2}}{{a}^{2}}-\frac{{\left(x-2\right)}^{2}}{16}=1
Podemos encontrar el valor de {a}^{2} sustituyendo el punto dado por el enunciado.
\frac{{1}^{2}}{{a}^{2}}-\frac{{\left(4-2\right)}^{2}}{16}=1\to \frac{1}{{a}^{2}}-\frac{4}{16}=1
Despejando.
\frac{1}{{a}^{2}}=1+\frac{4}{16}\to {a}^{2}=\frac{4}{5}
Sustituimos en la ecuación ordinaria.
\frac{5{y}^{2}}{4}-\frac{{\left(x-2\right)}^{2}}{16}=1
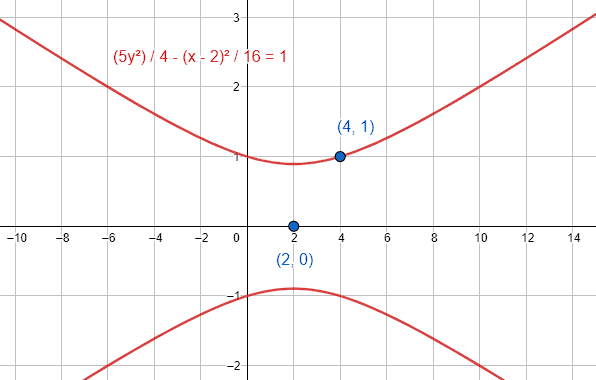
La respuesta correcta es el inciso c).
Reactivo 48
Calcule las coordenadas de los vértices de la hipérbola:
\frac{{\left(y-2\right)}^{2}}{4}-\frac{{\left(x-1\right)}^{2}}{16}=1
- {v}_{1}=\left(-1, 4\right) y {v}_{2}=\left(-1, 0\right)
- {v}_{1}=\left(1, 4\right) y {v}_{2}=\left(1, 0\right)
- {v}_{1}=\left(1, -4\right) y {v}_{2}=\left(1, 0\right)
- {v}_{1}=\left(4, 1\right) y {v}_{2}=\left(0, 1\right)
Solución:
Similar a una parábola, los lóbulos de una hipérbola poseen cada una un vértice, en el mismo eje del centro y los focos.
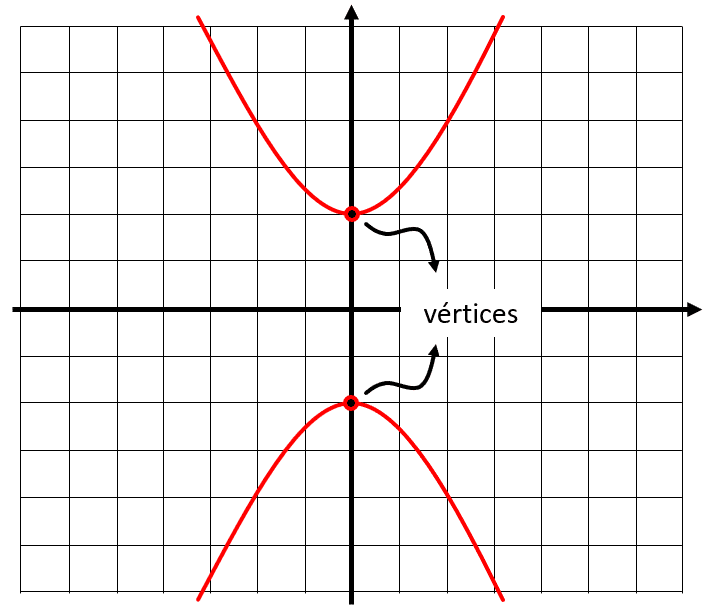
Debido a que el término con y es positivo, la hipérbola es vertical. Las coordenadas de los vértices serían:
{v}_{\mathrm{1,2}}=\left(h, k\pm a\right)
Donde a es la magnitud del semieje real que vale 2 para este caso.
{v}_{1}=\left(1, 4\right) y {v}_{2}=\left(1, 0\right)
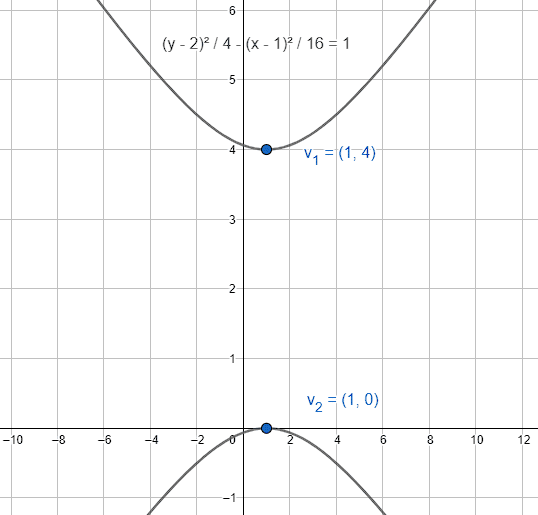
La respuesta correcta es el inciso b).
Reactivo 49
Obtenga la ecuación de las asíntotas para la hipérbola que se muestra en la figura.
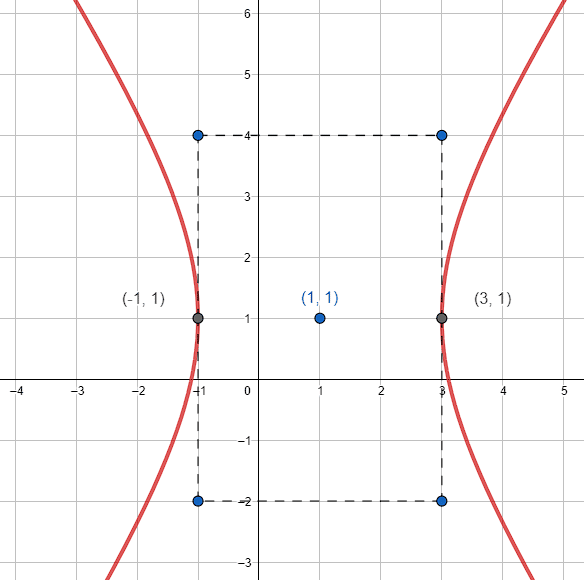
- y=\pm \frac{3}{2}\left(x-1\right)+1
- y=\pm \frac{3}{2}\left(x+1\right)+1
- y=\pm \frac{3}{2}\left(x-1\right)-1
- y=\pm \frac{3}{2}\left(x+1\right)-1
Solución:
Las asíntotas de una hipérbola, son dos rectas oblicuas que pasan por el centro de la misma y atraviesan las esquinas del rectángulo formado por el eje mayor y el menor. Sus pendientes son:
{m}_{1}=\frac{b}{a} y {m}_{2}=-\frac{b}{a}
Si la hipérbola estuviese centrada en el origen, las ecuaciones serían:
y=\pm \frac{b}{a}x
Pero como el centro no es el origen, la ecuación sería:
y-k=\pm \frac{b}{a}\left(x-h\right)
Sustituimos los valores dados por el enunciado. En este caso a=2 y b=3 según la gráfica.
y-1=\pm \frac{3}{2}\left(x-1\right)
{A}_{\mathrm{1,2}}:y=\pm \frac{3}{2}\left(x-1\right)+1
Resolviendo para cada caso:
{A}_{1}:y=\frac{3}{2}x-\frac{1}{2}=1.5x-0.5
{A}_{2}:y=-\frac{3}{2}x+\frac{5}{2}=-1.5x+2.5
Si graficamos nuestra solución nos queda:
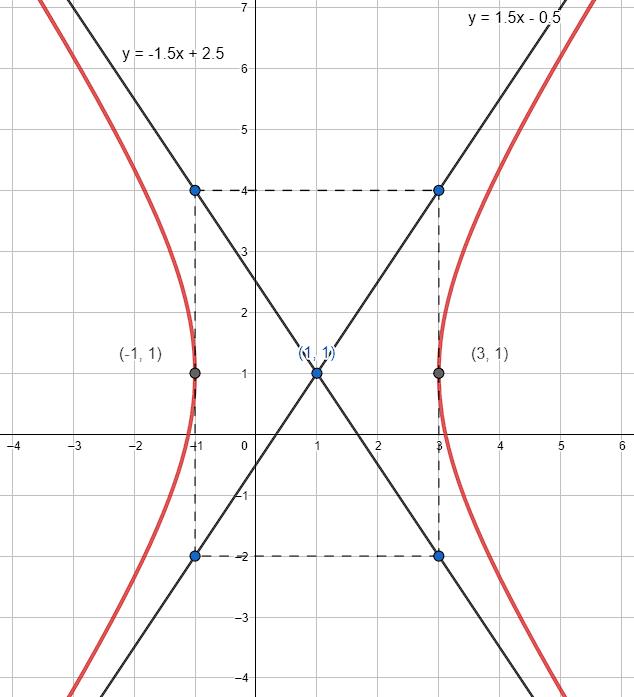
La respuesta correcta es el inciso a).
Reactivo 50
En la ecuación general de segundo grado, ¿cuál es el coeficiente responsable de la rotación de la cónica?
A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0
- A
- B
- C
- D
Solución:
Aplicando un cambio de coordenadas sobre la EGSG, se obtiene un sistema de ecuaciones paramétrica, que relaciona a los coeficientes de la EGSG con el ángulo de rotación entre los dos sistemas coordenados \theta . Simplificando e igualando expresiones, llegamos a la siguiente igualdad:
\mathrm{tan}2\theta =\frac{B}{A-C}
Si el coeficiente B es igual a cero, la tangente de 2\theta también se hace cero, por extensión, la aparición del término Bxy provoca rotaciones en la cónica.
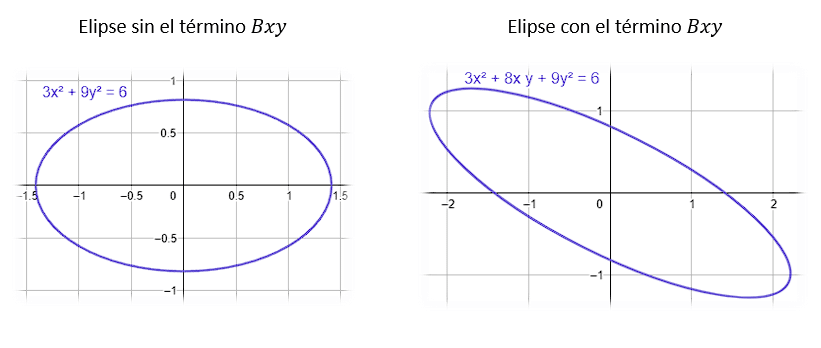
Concluimos que la respuesta correcta es el inciso b).