Guía UNAM Matemáticas: Área 1 Cs Físico-Matemáticas P. 3

¡Llegamos a la última parte aspirante! Continuamos con la solución de la tercera y última parte de los reactivos de matemáticas área 1, en este caso del 67 al 72, en la guía de Ciencias Físico Matemáticas e Ingenierías como preparación al examen de ingreso UNAM.

Te dejo un resumen de la prueba de ingreso a la UNAM:

• Desarrollo: UNAM
• Área 1: Ciencias Físico Matemáticas e Ingenierías
• Materia: Matemáticas
• Reactivos: 120
• Tipo: Opción múltiple
• Duración: 3 horas
• Modalidades: Presencial

¡Felicidades por llegar hasta aquí aspirante! Matemáticas parece una asignatura de fórmulas y despejes, pero en ella se encuentran los modelos para comprender el mundo que nos rodea.

Guía matemáticas UNAM área 1 resuelta

Vamos con los últimos 6 ejercicios de matemáticas de la guía Área 1 de Ciencias Físico Matemáticas e Ingenierías de la UNAM. Recuerda tomar descansos entre ejercicios, esto también forma parte del proceso de aprendizaje.

Reactivo 67

Se tiene que \underset{x\to a}{\mathrm{lim}}f\left(x\right)=k y \underset{x\to a}{\mathrm{lim}}g\left(x\right)=-k . Determine el \underset{x\to a}{\mathrm{lim}}\left[f\left(x\right)-g\left(x\right)\right] .

1. -{k}^{2}
2. 0
3. 2k
4. {k}^{2}

Solución:

Para resolver este límite, debemos aplicar la propiedad del límite de una suma.

\underset{x\to a}{\mathrm{lim}}\left[f\left(x\right)-g\left(x\right)\right]=\underset{x\to a}{\mathrm{lim}}f\left(x\right)-\underset{x\to a}{\mathrm{lim}}g\left(x\right)

Sustituimos el límite de cada función, dado por el enunciado.

\underset{x\to a}{\mathrm{lim}}f\left(x\right)-\underset{x\to a}{\mathrm{lim}}g\left(x\right)=k-\left(-k\right)=2k

La respuesta correcta es el inciso C.

Reactivo 68

La derivada de y=\mathrm{ln}\left({x}^{2}+5\right) es:

1. \frac{1}{{x}^{2}+5}
2. \frac{x}{{x}^{2}+5}
3. \frac{2x}{{x}^{2}-5}
4. \frac{2x}{{x}^{2}+5}

Solución:

Analizando la función mediante la regla de la cadena, determinamos que la función principal es la del logaritmo natural. Derivamos aplicando la fórmula para el logaritmo natural.

{y}^{\text{'}}={\left[\mathrm{ln}\left({x}^{2}+5\right)\right]}^{\text{'}}=\frac{{\left({x}^{2}+5\right)}^{\text{'}}}{{x}^{2}+5}

Resolvemos la derivada indicada aplicando la propiedad de la derivada de una suma, de una potencia y de una constante.

\frac{{\left({x}^{2}+5\right)}^{\text{'}}}{{x}^{2}+5}=\frac{2x}{{x}^{2}+5}

Finalmente:

{y}^{\text{'}}=\frac{2x}{{x}^{2}+5}

Comparando con los incisos, concluimos que la respuesta correcta es el D.

Reactivo 69

Si f\left(x\right)={e}^{\frac{3}{2}+x} ; determina {f}^{IV}\left(x\right) .

1. {f}^{IV}\left(x\right)=4{e}^{\frac{3}{2}+x}
2. {f}^{IV}\left(x\right)={e}^{\frac{3}{2}+x}
3. {f}^{IV}\left(x\right)=-{e}^{\frac{3}{2}+x}
4. {f}^{IV}\left(x\right)=-4{e}^{\frac{3}{2}+x}

Solución:

El enunciado solicita que calculemos la cuarta derivada de la función f\left(x\right) . Es decir, debemos derivar sucesivamente 4 veces; el resultado de una derivada lo volvemos a derivar. Así, hasta hacerlo 4 veces. En todos los casos se aplica la fórmula para derivar una exponencial.

Primera derivada.

{f}^{\text{'}}\left(x\right)={\left[{e}^{\frac{3}{2}+x}\right]}^{\text{'}}={\left(\frac{3}{2}+x\right)}^{\text{'}}{e}^{\frac{3}{2}+x}={e}^{\frac{3}{2}+x}

Con este resultado, vemos que {f}^{\text{'}} es exactamente igual a la función original. Como consecuencia de esto, al derivar una segunda vez, volveremos a obtener la función original f .

{f}^{\text{'}\text{'}}\left(x\right)={\left[{f}^{\text{'}}\left(x\right)\right]}^{\text{'}}, {f}^{\text{'}}=f\to {f}^{\text{'}\text{'}}\left(x\right)={\left[f\right]}^{\text{'}}={f}^{\text{'}}

\therefore {f}^{\text{'}\text{'}}\left(x\right)=f

Generalizando obtenemos:

{f}^{\left(n\right)}\left(x\right)=f\left(x\right)

Teniendo en cuenta todo lo anterior, la cuarta derivada {f}^{IV} es igual a  {e}^{\frac{3}{2}+x} . La respuesta correcta es el inciso B.

Reactivo 70

La pendiente de la tangente a la curva f\left(x\right)={e}^{3x} en el punto P\left(0, 1\right) es igual a

1. 0
2. 1
3. 2
4. 3

Solución:

Recordemos que la derivada de una función nos permite calcular la pendiente de la recta en cualquier punto de su dominio. En este caso, derivamos a la función dada y la evaluamos en x=0 para obtener la pendiente de la recta tangente en ese punto.

Aplicamos la fórmula de la derivada de la exponencial.

{f}^{\text{'}}\left(x\right)=3{e}^{3x}

Evaluemos.

m={f}^{\text{'}}\left(0\right)=3{e}^{3\left(0\right)}=\left(3\right)\left(1\right)=3

La pendiente de la recta tangente a f\left(x\right) en x=0 es igual a 3.

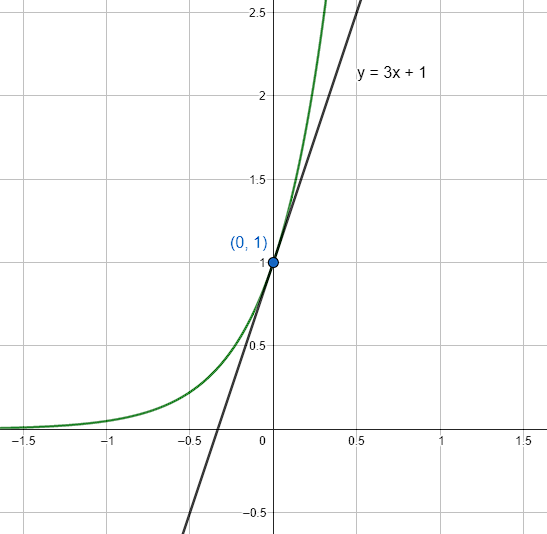
Indicamos como respuesta correcta al inciso D.

Reactivo 71

La solución de la integral \int \mathrm{cos}\left(8x\right)dx es:

1. -8\mathrm{sin}\left(x\right)+C
2. -8\mathrm{sin}\left(8x\right)+C
3. \frac{1}{8}\mathrm{sin}\left(x\right)+C
4. \frac{1}{8}\mathrm{sin}\left(8x\right)+C

Solución:

Para poder resolver esta integral, debemos tener el diferencial del argumento del coseno, es decir, el diferencial de 8x .

d\left(8x\right)=8dx

Solo nos falta el 8, multiplicamos y dividimos por este número para mantener la igualdad y construir el diferencial.

\int \mathrm{cos}\left(8x\right)dx=\frac{8}{8}\int \mathrm{cos}\left(8x\right)dx=\frac{1}{8}\int \mathrm{cos}\left(8x\right)8dx=\frac{1}{8}\int \mathrm{cos}\left(8x\right)d\left(8x\right)

Ahora, esta integral es inmediata.

\frac{1}{8}\int \mathrm{cos}\left(8x\right)d\left(8x\right)=\frac{1}{8}\mathrm{sin}\left(8x\right)+C

Finalmente:

\int \mathrm{cos}\left(8x\right)dx=\frac{1}{8}\mathrm{sin}\left(8x\right)+C

La respuesta correcta es el inciso D.

Reactivo 72

La solución de la integral indefinida \int \left(x+2\right)\left({e}^{{x}^{2}+4x+3}\right)dx es:

1. {e}^{{x}^{2}+4x+3}+C
2. {e}^{-\left({x}^{2}+4x+3\right)}+C
3. \frac{1}{2}{e}^{-\left({x}^{2}+4x+3\right)}+C
4. \frac{1}{2}{e}^{{x}^{2}+4x+3}+C

Solución:

Esta integral se puede resolver mediante artificios algebraicos o por cambio de variables. Debido a que el anterior reactivo se resolvió mediante artificios, este lo vamos a desarrollar aplicando cambio de variable.

El cambio se hará al exponente de la función exponencial.

u={x}^{2}+4x+3\to du=\left(2x+4\right)dx

Extraemos como factor común el 2.

du=2\left(x+2\right)dx\to \frac{1}{2}du=\left(x+2\right)dx

Aplicamos el cambio.

\int \left(x+2\right)\left({e}^{{x}^{2}+4x+3}\right)dx\to \frac{1}{2}\int {e}^{u}du

Resolvemos.

\frac{1}{2}\int {e}^{u}du=\frac{1}{2}{e}^{u}+C

Devolvemos el cambio.

\frac{1}{2}{e}^{u}+C\to \frac{1}{2}{e}^{{x}^{2}+4x+3}+C

Finalmente:

\int \left(x+2\right)\left({e}^{{x}^{2}+4x+3}\right)dx=\frac{1}{2}{e}^{{x}^{2}+4x+3}+C

La respuesta correcta es el inciso D.