Guía UNAM Matemáticas: Área 1 Cs Físico-Matemáticas

¡Hola aspirante! En este post estaremos resolviendo paso a paso los primeros 10 reactivos de matemáticas, del 47 al 56, correspondientes a la guía área 1 de Ciencias Físico Matemáticas e Ingenierías, como preparación antes del examen de ingreso a la UNAM.

¿Cómo estudiar la guía UNAM? Comienza por estudiar el temario de matemáticas UNAM área 1, luego que domines el contenido ven y resuelve los ejercicios sin mirar la solución.

A continuación, te dejo un breve resumen con los puntos más importantes del examen de ingreso a la UNAM.

• Desarrollo: UNAM
• Área 1: Ciencias Físico Matemáticas e Ingenierías
• Materia: Matemáticas
• Reactivos: 120
• Tipo: Opción múltiple
• Duración: 3 horas
• Modalidades: Presencial

El porcentaje de rechazados por área 1 es del 90%. Si estudias con disciplina y tiempo, podrás formar parte del 10% que ingresan a la UNAM.

Estructura del examen

La prueba de ingreso a la Universidad Nacional Autónoma de México tiene una extensión de 120 ejercicios, de los cuales 26 pertenecen a la asignatura de matemáticas para el área 1 Ciencias Físico Matemáticas e Ingenierías.

En la siguiente tabla, encontrarás la estructura del examen a la UNAM por el área 1, donde se indican las asignaturas y la cantidad de reactivos correspondientes a resolver.

Temas	Área 1
Español	18
Matemáticas	26
Física	16
Química	10
Biología	10
Historia universal	10
Historia de México	10
Literatura	10
Geografía	10
Filosofía	NA
Total	120

¿Sabías que en área 1, la carrera con el mayor número de aciertos obligatorios es ingeniería aeroespacial con 114?

De las 39 carreras ofertadas por la UNAM para el área 1, nueve de ellas cuentan con modalidad de ingreso indirecto, es decir, deberás cumplir una serie de requisitos extra que dependerán de la facultad a la que desees ingresar.

¿Cómo estudiar matemáticas?

Si estás saliendo del bachillerato, probablemente sea común para ti estudiar matemáticas resolviendo montones de ejercicios y leyendo unos pocos apuntes, pero la realidad de las matemáticas en la universidad está (por mucho) lejos de eso.

Desde ahora, no es relevante la cantidad de ejercicios resueltos en tu cuaderno, lo realmente valioso será tu capacidad para analizar los problemas.

Los siguientes consejos te permitirán estudiar matemáticas manteniendo presente lo anterior.

Guía matemáticas UNAM área 1 resuelta

Vamos con la solución paso a paso de los primeros 10 reactivos de matemáticas, para la guía UNAM del área de Ciencias Físico Matemáticas e Ingenierías.

Durante el examen no se permite el uso de calculadora, resuelve los problemas sin ella para adecuarte a las condiciones reales del examen.

Reactivo 47

A las 3 a.m. de un día de invierno se reporta una temperatura de –3 °C, a las 12 del día la temperatura ya es de 15 °C, ¿de cuántos grados fue la diferencia de temperaturas?

1. 18 °C
2. 12 °C
3. -18 °C
4. -12 °C

Solución:

Para calcular la diferencia de temperatura, restamos al segundo registro con el primero.

\mathrm{\Delta }T={T}_{2}-{T}_{1}=15-\left(-3\right)=18 °\mathrm{C}

La respuesta correcta es el inciso A.

Reactivo 48

La expresión {\left(\frac{{a}^{n}}{{a}^{m}}\right)}^{n} se reduce a:

1. {a}^{n}-{a}^{nm}
2. {a}^{{n}^{2}-mn}
3. {a}^{2n-mn}
4. {a}^{2n}-{a}^{nm}

Solución:

Para hallar la forma simplificada de la expresión, debemos aplicar las propiedades de los exponentes correspondientes. Debido a que en el interior de los paréntesis se encuentra un cociente de potencias de igual base, empleamos la propiedad que lleva el mismo nombre.

{\left(\frac{{a}^{n}}{{a}^{m}}\right)}^{n}={\left({a}^{n-m}\right)}^{n}

Ahora aplicamos la propiedad de potencia de una potencia.

{\left({a}^{n-m}\right)}^{n}={a}^{n\left(n-m\right)}={a}^{{n}^{2}-nm}

Finalmente:

{\left(\frac{{a}^{n}}{{a}^{m}}\right)}^{n}={a}^{{n}^{2}-nm}

Concluimos indicando como respuesta correcta al inciso B.

Reactivo 49

Al desarrollar {\left({x}^{2}-3y\right)}^{3} se obtiene:

1. {x}^{6}-9{x}^{4}y+27{x}^{2}{y}^{2}+27{y}^{3}
2. {x}^{6}+9{x}^{4}y-27{x}^{2}{y}^{2}+27{y}^{3}
3. {x}^{6}-9{x}^{4}y+27{x}^{2}{y}^{2}-27{y}^{3}
4. {x}^{6}+9{x}^{4}y-27{x}^{2}{y}^{2}-27{y}^{3}

Solución:

Para encontrar la expansión del binomio al cubo, empleamos el siguiente producto notable:

{\left(a-b\right)}^{3}={a}^{3}-3{a}^{2}b+3a{b}^{2}-{b}^{3}

En nuestro caso: a={x}^{2} y b=3y . Aplicando el producto notable a la expresión nos queda:

{\left({x}^{2}-3y\right)}^{3}={\left({x}^{2}\right)}^{3}-3{\left({x}^{2}\right)}^{2}\left(3y\right)+3\left({x}^{2}\right){\left(3y\right)}^{2}-{\left(3y\right)}^{3}

Simplificamos.

{\left({x}^{2}\right)}^{3}-3{\left({x}^{2}\right)}^{2}\left(3y\right)+3\left({x}^{2}\right){\left(3y\right)}^{2}-{\left(3y\right)}^{3}={x}^{6}-9{x}^{4}y+27{x}^{2}{y}^{2}-27{y}^{3}

Finalmente:

{\left({x}^{2}-3y\right)}^{3}={x}^{6}-9{x}^{4}y+27{x}^{2}{y}^{2}-27{y}^{3}

Comparando con los incisos, la respuesta correcta es el inciso C.

Reactivo 50

Al simplificar \frac{{x}^{2}-5x+6}{2ax-6a} se obtiene:

1. \frac{\left(x-2\right)\left(x-3\right)}{2a}
2. \frac{x-3}{2a\left(x-2\right)}
3. \frac{x-2}{2a}
4. \frac{\left(x-2\right)\left(x+3\right)}{2a}

Solución:

Este reactivo puede resolverse sin factorizar la expresión, sólo con análisis. Veamos que en el numerador hay un trinomio de segundo grado y en el denominador un binomio, del que se puede extraer factor común 2a .

Debido a que al factorizar quedarán dos factores lineales arriba y uno abajo, los posibles resultados son: no poder simplificar nada o, simplificar el factor del denominador con uno de los factores lineales del numerador, quedando un solo factor lineal arriba.

Examinando a los incisos, ninguna de las opciones muestra dos factores lineales arriba y uno abajo, solo muestran la segunda opción: un factor lineal arriba. Por lo tanto y a partir de este análisis, la respuesta correcta es el inciso C.

Sin embargo, este es un truco para el examen. Vamos a realizar el desarrollo para comprobar nuestro análisis. Factorizamos el trinomio del numerador buscando dos números que sumados sean -5 y que multiplicados +6, estos deben ser: -2 y -3.

\frac{{x}^{2}-5x+6}{2ax-6a}=\frac{\left(x-2\right)\left(x-3\right)}{2a\left(x-3\right)}

Simplificamos.

\frac{\left(x-2\right)\left(x-3\right)}{2a\left(x-3\right)}=\frac{x-2}{2a}

La respuesta correcta es el inciso C.

Reactivo 51

La expresión 2x+3=7 es una:

1. Inecuación
2. Desigualdad
3. Ecuación
4. Identidad

Solución:

La expresión del enunciado es una ecuación. Recordemos que las ecuaciones son expresiones algebraicas que son ciertas para un conjunto finito de valores de x . La igualdad del enunciado es cierta sólo cuando x=2 .

2\left(2\right)+3=4+3=7

La respuesta correcta es el inciso C.

Reactivo 52

Las raíces de la ecuación 2{x}^{2}+5x-3=0 son:

1. -2, 3
2. -3, 1/2
3. 3, -1/2
4. 2, -3

Solución:

En este caso, no es posible factorizar con el truco de buscar dos números que sumados sean +5 y multiplicados -3, porque el coeficiente de {x}^{2} es distinto de 1. Empleamos entonces la fórmula de segundo grado.

2{x}^{2}+5x-3=0\to a=2, b=5, c=-3

{x}_{\mathrm{1,2}}=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}

Sustituyendo:

{x}_{\mathrm{1,2}}=\frac{-5\pm \sqrt{{5}^{2}-4\left(2\right)\left(-3\right)}}{2\left(2\right)}=\frac{-5\pm \sqrt{25+24}}{4}=\frac{-5\pm \sqrt{49}}{4}=\frac{-5\pm 7}{4}

Finalmente:

{x}_{1}=\frac{-5+7}{4}=\frac{2}{4}=\frac{1}{2}

{x}_{2}=\frac{-5-7}{4}=-\frac{12}{4}=-3

Las raíces del polinomio son: -3, 1/2.

La respuesta correcta es el inciso B.

Reactivo 53

La solución de la desigualdad 3x-5>x+6 es:

1. x>\frac{11}{2}
2. x>-\frac{11}{2}
3. x>\frac{2}{11}
4. x>-\frac{2}{11}

Solución:

Iniciamos agrupando la x en el primer miembro y a los términos independientes en el segundo.

3x-5>x+6\to 3x-x>6+5

Simplificamos.

2x>11

Dividimos ambos miembros por +2. Debido a que el número es positivo, la desigualdad se mantiene.

x>\frac{11}{2}

Indicamos como respuesta correcta al inciso A.

Reactivo 54

Soluciona el sistema de ecuaciones:

\left\{\begin{array}{c}5x+2y-z=-7\\ x-2y+2z=0\\ 3y+z=17\end{array}\right.

1. x=-2, y=3, z=5
2. x=2, y=4, z=-5
3. x=-2, y=4, z=5
4. x=2, y=3, z=-5

Solución:

Este sistema de ecuaciones se puede resolver de varias maneras: sustitución, igualación, eliminación o mediante determinantes. Debido a que el sistema es de 3×3, el método por determinantes es el más adecuado. Iniciamos calculando el determinante del sistema.

{\mathrm{\Delta }}_{s}=\left|\begin{array}{ccc}5& 2& -1\\ 1& -2& 2\\ 0& 3& 1\end{array}\right|=\left|\begin{array}{cc}-2& 2\\ 3& 1\end{array}\right|\left(5\right)-\left|\begin{array}{cc}1& 2\\ 0& 1\end{array}\right|\left(2\right)+\left|\begin{array}{cc}1& -2\\ 0& 3\end{array}\right|\left(-1\right)

{\mathrm{\Delta }}_{s}=\left(-2-6\right)\left(5\right)-\left(1-0\right)\left(2\right)+\left(3-0\right)\left(-1\right)=-40-2-3

{\mathrm{\Delta }}_{s}=-45

Ahora calculamos el determinante de y . Sustituimos a la columna de las y por los términos independientes. Luego explicaremos por qué primero y y no x .

{\mathrm{\Delta }}_{y}=\left|\begin{array}{ccc}5& -7& -1\\ 1& 0& 2\\ 0& 17& 1\end{array}\right|=\left|\begin{array}{cc}0& 2\\ 17& 1\end{array}\right|\left(5\right)-\left|\begin{array}{cc}1& 2\\ 0& 1\end{array}\right|\left(-7\right)+\left|\begin{array}{cc}1& 0\\ 0& 17\end{array}\right|\left(-1\right)

{\mathrm{\Delta }}_{y}=\left(0-34\right)\left(5\right)-\left(1-0\right)\left(-7\right)+\left(17-0\right)\left(-1\right)

{\mathrm{\Delta }}_{y}=-170+7-17=-180

El valor de y sería:

y=\frac{{\mathrm{\Delta }}_{y}}{{\mathrm{\Delta }}_{s}}=\frac{-180}{-45}=4

Con este resultado descartamos a los incisos a y d. Para decidir entre b y c, sustituimos el valor de y en la tercera ecuación y calculamos a z .

3y+z=17\to z=17-3y

\therefore z=17-3\left(4\right)=5

y=4, z=5

Esta información es suficiente para concluir que la respuesta es el inciso c). Resolviendo el sistema de esta manera, ahorramos calcular 2 determinantes.

Reactivo 55

Encuentra el dominio de la función que tiene regla de correspondencia f\left(x\right)={x}^{2}+1 y rango {R}_{f}=\forall f\left(x\right)\in \left[1, 17\right] .

1. {D}_{f}=\forall x\in \left[0, 4\right]
2. {D}_{f}=\forall x\in \left(0, 4\right)
3. {D}_{f}=\forall x\in \left(-4, 4\right)
4. {D}_{f}=\forall x\in \left[-4, 4\right]

Solución:

La función del enunciado es una parábola, cuyo dominio es todos los reales. Debido a que nos acotan el rango entre \left[1, 17\right] , debemos obtener los valores de x correspondientes que acotan al dominio.

La función es una parábola que abre hacia arriba porque el término cuadrático es positivo. Además, el punto más bajo o vértice se encuentra en \left(0, 1\right) . Esto quiere decir que el dominio para el rango indicado se obtiene con el extremo superior.

17={x}^{2}+1\to {x}^{2}=16\to x=\pm 4

Para que el rango de la función sea \left[1, 17\right] , la variable x debe encontrarse entre -4 y 4.

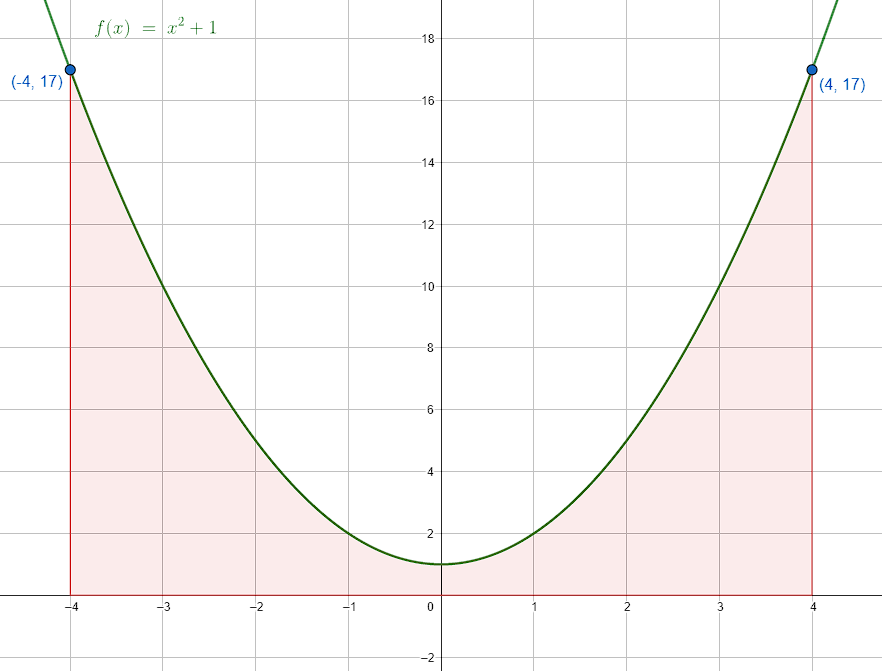
{D}_{f}=\forall x\in \left[-4, 4\right]

La respuesta correcta es el inciso D.

Reactivo 56

¿A cuántos grados equivalen \frac{11\pi }{18} radianes?

1. 220°
2. 110°
3. 169°
4. 198°

Solución:

Para transformar de radianes a grados, utilizamos la siguiente ecuación:

{\theta }_{°}=\frac{180}{\pi }{\theta }_{r}

Sustituimos.

{\theta }_{°}=\frac{180}{\pi }\left(\frac{11\pi }{18}\right)=110°

La respuesta correcta es el inciso B.

Temario matemáticas área 1

En la siguiente lista tienes el temario de matemáticas para el área 1 de Ciencias Físico Matemáticas UNAM. Puede parecer extenso, pero si organizas tu tiempo podrás cubrir cada uno de los temas.