¡Hola de nuevo aspirante! Vamos con la solución de la segunda parte de los reactivos de matemáticas para el área 1, del 57 al 66, en la guía de Ciencias Físico Matemáticas e Ingenierías referente al examen de ingreso a la UNAM.
El siguiente es un resumen de la prueba de ingreso a la UNAM:
- Desarrollo: UNAM
- Área 1: Ciencias Físico Matemáticas e Ingenierías
- Materia: Matemáticas
- Reactivos: 120
- Tipo: Opción múltiple
- Duración: 3 horas
- Modalidades: Presencial
Aunque matemáticas sea extensa, es importante que comprendas muy bien el temario porque representa el pilar de todas las carreras de la UNAM que pertenecen al área 1
Curso UNAM 2025
Guía matemáticas UNAM área 1 resuelta
Continuamos resolviendo los siguientes 10 reactivos de matemáticas de la guía de Ciencias Físico Matemáticas e Ingenierías de la UNAM.
Reactivo 57
En un triángulo rectángulo, la hipotenusa mide 6 unidades y uno de sus ángulos es de 30°. ¿Cuántas unidades mide el lado opuesto al ángulo dado?
- 4
- 4\sqrt{3}
- 3
- 4\sqrt{3}
Solución:
Hagamos una representación gráfica del triángulo planteado por el enunciado.
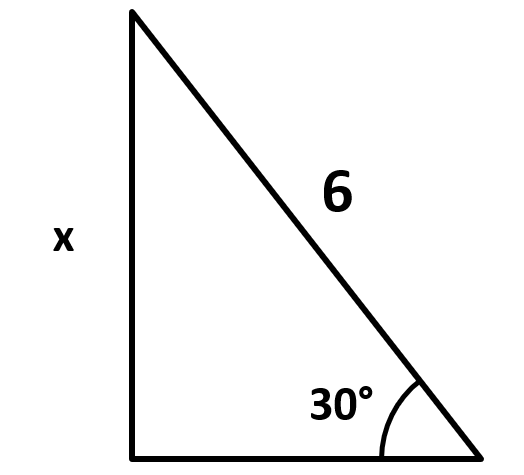
Calculamos a x aplicando la relación trigonométrica seno respecto al ángulo de 30°.
\mathrm{sin}30°=\frac{x}{6}\to x=6\mathrm{sin}30°
El seno de 30° es \frac{1}{2} . Finalmente:
x=6\left(\frac{1}{2}\right)=3 \mathrm{u}\mathrm{n}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{d}\mathrm{e}\mathrm{s}
La respuesta correcta es el inciso C.
Reactivo 58
Calcula el rango de la función y={e}^{\left(6x-\frac{1}{6}\right)}+6 .
- \left(6, \infty \right)
- \left(-6, \infty \right)
- \left[-\frac{1}{6}, \infty \right)
- \left[\frac{1}{6}, \infty \right)
Solución:
Para calcular el rango de una función, el procedimiento es:
- Obtener la inversa {f}^{-1} de la función.
- Calcular el dominio de la función inversa.
- El resultado obtenido es el rango de f .
En este caso, podemos ahorrarnos todo el procedimiento con solo analizar la función. Iniciemos recordando que las funciones exponenciales no dan valores negativos, ellas se encuentran acotadas entre 0 e infinito.
Al sumarle 6 a la función exponencial, estamos desplazando el mínimo valor que la función puede arrojar de cero a +6. Finalmente, debemos verificar los posibles valores que arroja el exponente de la exponencial.
Debido a que 6x-\frac{1}{6} es una línea recta, las imágenes que arroja una función lineal van desde -\infty hacia +\infty , por lo tanto, la exponencial va a recibir todos los posibles valores del eje real como exponente. Esto lo resaltamos para hacer notar que 6x-\frac{1}{6} no acotará al dominio de {e}^{\left(6x-\frac{1}{6}\right)} .
Con este análisis sistemático de la función, concluimos que el rango de \mathrm{ }y={e}^{\left(6x-\frac{1}{6}\right)}+6 es \left(6, \infty \right) .
{R}_{f}=\forall f\left(x\right)\in \left(6, \infty \right)
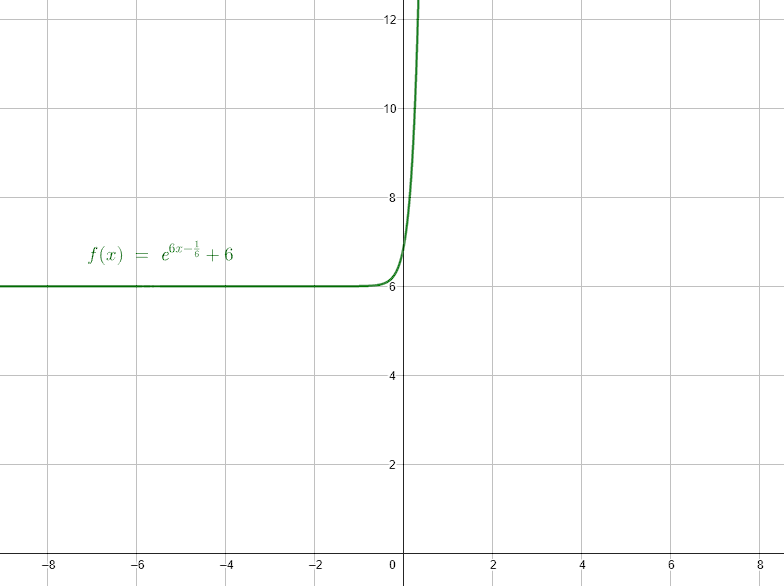
La respuesta correcta es el inciso A. De igual forma, vamos a realizar el cálculo correspondiente, pero sin hacer énfasis en los detalles.
Cálculo de la inversa.
f\left(x\right)={e}^{\left(6x-\frac{1}{6}\right)}+6\to {f}^{-1}=\frac{1}{6}\mathrm{ln}\left(y-6\right)-\frac{1}{36}
Dominio de la función inversa.
y-6>0\to y>6
El rango de la inversa (dominio de la inversa) es:
{R}_{f}=\forall f\left(x\right)\in \left(6, \infty \right)
Reactivo 59
Encuentra las coordenadas del punto S que divide por la mitad al segmento conformado por los puntos P(–1, 2) y Q(–2, 5) .
- S\left(-0.5, 3.5\right)
- S\left(-1.5, 2.5\right)
- S\left(-2.5, 3.5\right)
- S\left(-1.5, 3.5\right)
Solución:
Para calcular el punto que divide a la mitad a un segmento con extremos en P y Q , se utiliza la siguiente ecuación:
M=\left(\frac{{P}_{x}+{Q}_{x}}{2}, \frac{{P}_{y}+{Q}_{y}}{2}\right)
Sustituimos las coordenadas de los extremos.
M=\left(\frac{-1-2}{2}, \frac{2+5}{2}\right)=\left(\frac{-3}{2}, \frac{7}{2}\right)=\left(-1.5, 3.5\right)
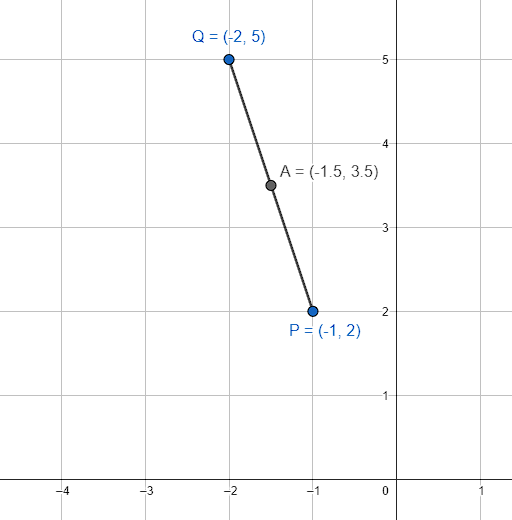
Concluimos indicando como respuesta correcta al inciso D.
Reactivo 60
¿Cuál es la ecuación de la recta que pasa por el punto P (5, 2) y es paralela a la recta que pasa por los puntos Q (2, –6) y R (–1, 3)?
- y=-2x-9
- y=-4x+3
- y=-5x-11
- y=-3x+17
Solución:
Para obtener la ecuación de una recta, necesitamos un punto y la pendiente. Debido a que el segmento que une a los puntos Q (2, –6) y R (–1, 3), es paralela a la recta que pasa por el punto P , la pendiente de esta última recta es la misma que para Q (2, –6) y R (–1, 3).
m=\frac{3+6}{-1-2}=\frac{9}{-3}=-3
Sustituimos en la ecuación punto – pendiente los valores obtenidos.
y-{y}_{o}=m\left(x-{x}_{o}\right)\to y-2=-3\left(x-5\right)
y=-3x+15+2
\therefore y=-3x+17
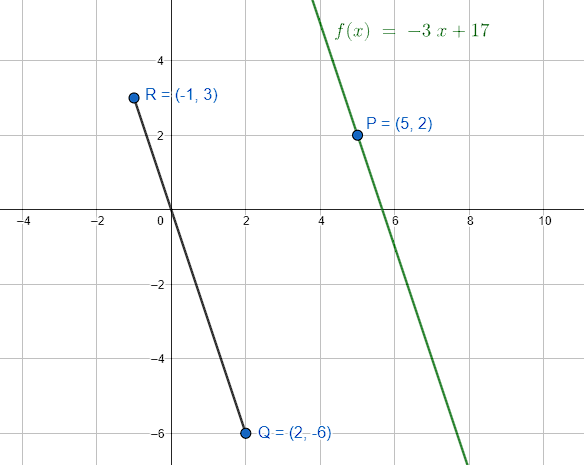
La respuesta correcta es el inciso D.
Reactivo 61
La ecuación ordinaria de la mediana del siguiente triángulo, trazada desde el vértice A es:
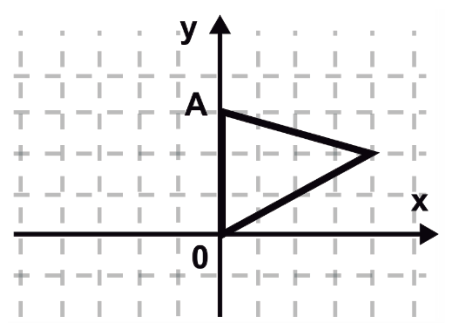
- y=-2x+3
- y=-x+3
- y=-\frac{1}{4}x+3
- y=-\frac{1}{2}x+3
Solución:
Las medias de un triángulo son segmentos de recta que van desde el punto medio de una arista hacia el vértice opuesto. En este caso, el vértice es el punto A y la arista es la que pasa por el origen O .
A partir de la gráfica, obtenemos las coordenadas del punto medio M .
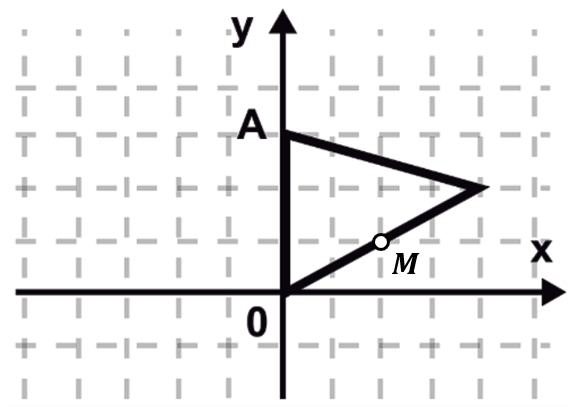
Los puntos que pasan por la recta son: A\left(0, 3\right) y M\left(\mathrm{2,1}\right) .
Calculamos la pendiente de la recta.
m=\frac{1-3}{2-0}=\frac{-2}{2}=-1
Sustituimos en la ecuación punto pendiente al punto A y la pendiente.
y-{y}_{o}=m\left(x-{x}_{o}\right)\to y-3=\left(-1\right)\left(x-0\right)
y=-x+3
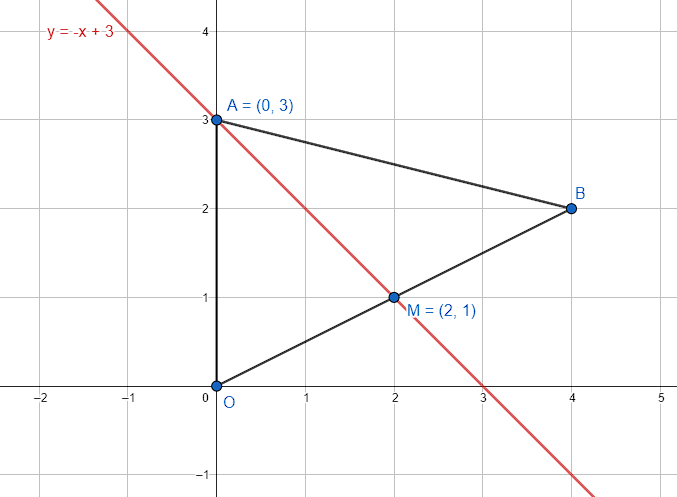
Indicamos como respuesta correcta al inciso B.
¿Ya conoces todos los detalles de la convocatoria UNAM 2023?
Todo sobre la convocatoria UNAM.
Reactivo 62
Considerando a la circunferencia como lugar geométrico, ¿qué expresión algebraica cumple que las coordenadas de los puntos P(x, y) cuya distancia al origen es 10?
- {x}^{2}+{y}^{2}+100=0
- {x}^{2}+{y}^{2}+10=0
- {x}^{2}+{y}^{2}-100=0
- {x}^{2}+{y}^{2}-10=0
Solución:
La ecuación ordinaria de una circunferencia es:
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
Donde \left(h, k\right) son las coordenadas del centro y r es el centro. El enunciado indica quien es el centro y el radio en esta frase: …cuya distancia al origen es 10. El centro es el origen \left(0, 0\right) y el radio es r=10 . Sustituimos en la ecuación:
{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}={10}^{2}\to {x}^{2}+{y}^{2}=100
{x}^{2}+{y}^{2}-100=0
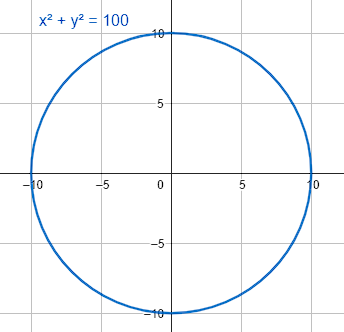
La respuesta correcta es el inciso C.
Todo sobre el examen y la guía UNAM
Reactivo 63
¿Cuál es la ecuación de la parábola con vértice en el origen, eje focal paralelo al eje Y que pasa por el punto P(4, –2) ?
- {x}^{2}=-8y
- {y}^{2}=8x
- {y}^{2}=-8x
- {x}^{2}=8y
Solución:
Teniendo en cuenta que el vértice está situado en el origen, y que el punto por el que pasa la parábola está por debajo del vértice, concluimos que la parábola abre hacia abajo. El signo del parámetro 4p debe ser negativo.
4py={x}^{2}
Calculamos el valor de p sustituyendo el punto dado.
4p\left(-2\right)={\left(4\right)}^{2}\to 4p=\frac{16}{-2}=-8
Sustituimos.
-8y={x}^{2}
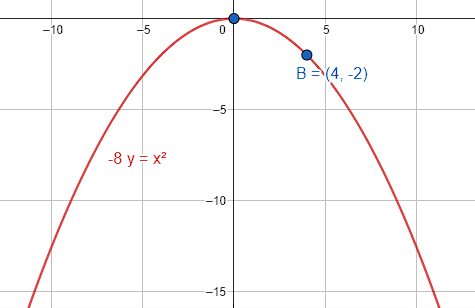
La respuesta correcta es el inciso A.
Número de aciertos por carrera
Reactivo 64
De las siguientes ecuaciones, ¿cuál tiene los valores de a, b y c iguales a la elipse \frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1 ?
- 4{x}^{2}+{y}^{2}-16=0
- {x}^{2}+4{y}^{2}+16=0
- {x}^{2}+4{y}^{2}-16=0
- 4{x}^{2}+4{y}^{2}+16=0
Solución:
En este caso, vamos a transformar a la elipse de su forma ordinaria a su forma general, para finalmente comparar el resultado con los incisos.
Multiplicamos toda la expresión por 16 para eliminar las fracciones.
\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1\to {x}^{2}+4{y}^{2}=16
Finalmente:
{x}^{2}+4{y}^{2}-16=0
Este resultado corresponde con el inciso C, por lo tanto, la ecuación que allí se muestra tiene los mismos valores de a, b y c que \frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1 .
Reactivo 65
Determina las coordenadas de los focos de la siguiente hipérbola.
\frac{{\left(x-4\right)}^{2}}{16}-\frac{{\left(y+1\right)}^{2}}{9}=1
- F\left(4, 2\right);{F}^{\text{'}}\left(4,-4\right)
- F\left(0, -1\right);{F}^{\text{'}}\left(8,-1\right)
- F\left(-1, 1\right);{F}^{\text{'}}\left(8, 1\right)
- F\left(-1, -1\right);{F}^{\text{'}}\left(9,-1\right)
Solución:
Para obtener las coordenadas de los focos de la hipérbola, debemos identificar en qué dirección se encuentra orientado el eje focal. Debido a que el término con x es positivo, el eje focal es paralelo al eje de las abscisas.
En base a lo anterior, las coordenadas de los focos son:
{F}_{\mathrm{1,2}}\left(h\pm c, k\right)
Donde \left(h, k\right) son las coordenadas del centro y c es la distancia entre los vértices y los focos. Examinando la ecuación:
\left(h, k\right)=\left(4, -1\right)
El parámetro c se calcula como:
{c}^{2}={a}^{2}+{b}^{2}\to c=\sqrt{16+9}=5
Finalmente:
{F}_{\mathrm{1,2}}\left(4\pm 5, -1\right)\to \left\{\begin{array}{c}{F}_{1}\left(9, -1\right)\\ {F}_{2}\left(-1, -1\right)\end{array}\right.
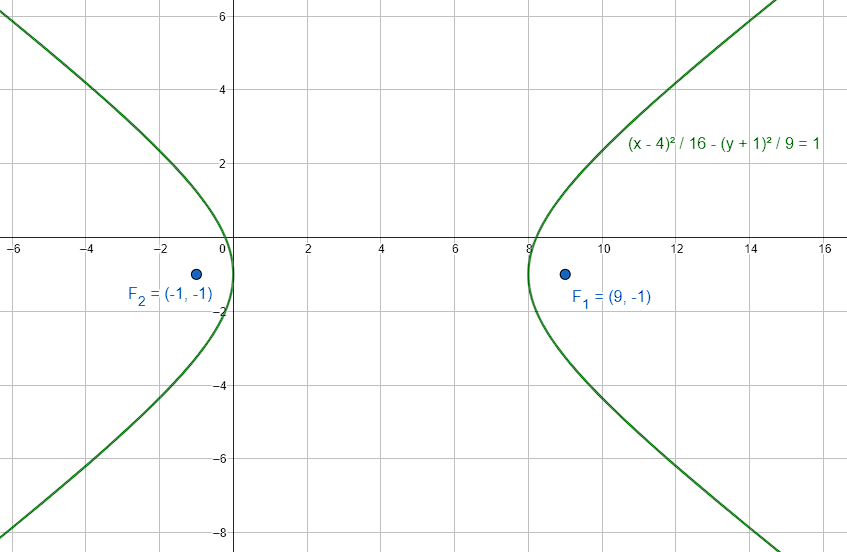
La respuesta correcta es el inciso D.
¿Vas a presentar la prueba de ingreso a la UNAM y no sabes qué son las carreras de ingreso indirecto?
Reactivo 66
Si la ecuación A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0 el discriminante {B}^{2}-4AC es positivo, entonces la ecuación representa una:
- Circunferencia
- Parábola
- Elipse
- Hipérbola
Solución:
El determinante de la ecuación general de segundo grado es una relación bastante útil que permite, entre otras cosas, establecer el tipo de cónica según el signo de A y C . Para el caso particular del enunciado, el determinante es positivo cuando A y C difieren de signo.
Si hacemos cero a B , ya que este coeficiente es responsable de rotaciones en la cónica, nos queda:
{B}^{2}-4AC\to B=0\to -4AC
Para A positivo y C negativo:
-4\left(+A\right)\left(-C\right)\to 4AC>0
Trasladando esto a la ecuación general:
A{x}^{2}-C{y}^{2}+Dx+Ey+F=0
Solo en la hipérbola, el signo de las variables es distinto. Concluimos entonces:
Cuando {B}^{2}-4AC>0 , la cónica es una hipérbola.
La respuesta correcta es el inciso D. Esto se pudo responder de forma más reducida con solo conocer la convención de signos del determinante, pero el motivo de estas soluciones es que entiendas de dónde sale cada cosa.
