Continuamos resolviendo los reactivos del 31 al 40, de la cuarta parte del simulador de matemáticas (segunda versión)como preparación al examen de ingreso IPN en el área de Ingeniería y Ciencias Físico Matemáticas.

Ejercicios de Matemáticas
Vamos con los reactivos del 31 al 40 del simulador de matemáticas, para la prueba de ingreso del Instituto Politécnico Nacional.
Reactivo 31
Identificar si la función f\left(x\right)=\frac{x}{\left|x\right|} , es continua o discontinua en x=0 .
- Discontinuidad no evitable
- Discontinuidad evitable
- Continua a tramos
- Continua en todo su dominio
Solución:
Para comprobar que una función sea continua en un punto x={x}_{o} , se deben cumplir dos condiciones:
- Que la función exista y esté definida en el punto
- Que el límite cuando x\to {x}_{o} de f\left(x\right) y sea igual a f\left({x}_{o}\right)
Si al menos una de las condiciones no se cumple, la función es discontinua en {x}_{o} . Al intentar comprobar la segunda condición, nos encontramos que el límite por la izquierda (-1) es distinto al límite por la derecha (1) para f\left(x=0\right) .
Por esta razón, la función es discontinua en x=0 .
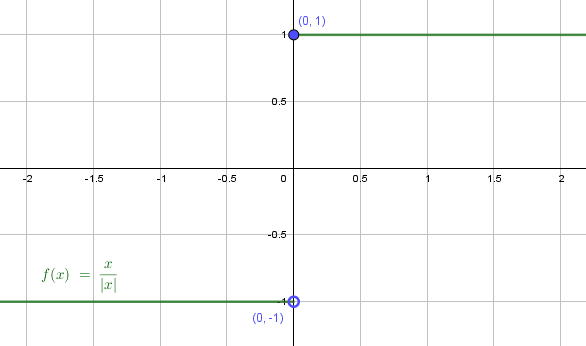
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 32
Calcule el conjunto solución de la siguiente inecuación:
\left|\frac{1}{3x+1}\right|<3
- \left(-\infty , -\frac{4}{9}\right)
- \left(-\infty , -\frac{4}{9}\right)\cup \left(-\frac{2}{9}, \infty \right)
- \left(-\frac{2}{9}, \infty \right)
- \left(-\infty , \frac{4}{9}\right)\cup \left(\frac{2}{9}, \infty \right)
Solución:
Para estudiar las inecuaciones con valor absoluto, primero debemos descomponerlas en una inecuación doble.
\left|\frac{1}{3x+1}\right|<3\to -3<\frac{1}{3x+1}<3
Esto nos arroja dos inecuaciones por resolver:
\left\{\begin{array}{c}{I}_{1}: \frac{1}{3x+1}>-3\\ {I}_{2}: \frac{1}{3x+1}<3\end{array}\right.
La solución total será la unión entre las soluciones parciales de ambas inecuaciones. Vamos con la primera.
Inecuación 1.
\frac{1}{3x+1}>-3
Pasamos el -3 al otro miembro y resolvemos la suma.
\frac{1}{3x+1}+3>0\to \frac{9x+4}{3x+1}>0
La fracción será positiva cuando ambos, numerador y denominador, sean positivos o negativos.
{S}_{11}: 9x+4>0 \mathrm{y}\mathrm{ }3x+1>0
{S}_{12}: 9x+4<0 \mathrm{y}\mathrm{ }3x+1<0
Resolviendo {S}_{11} :
9x>-4 \mathrm{y}\mathrm{ }3x>-1\to x>-\frac{4}{9} \mathrm{y}\mathrm{ }x>-\frac{1}{3}

{S}_{11}=\left(-\frac{1}{3}, \infty \right)
Resolviendo {S}_{12} :
9x<-4 \mathrm{y}\mathrm{ }3x<-1\to x<-\frac{4}{9} \mathrm{y}\mathrm{ }x<-\frac{1}{3}
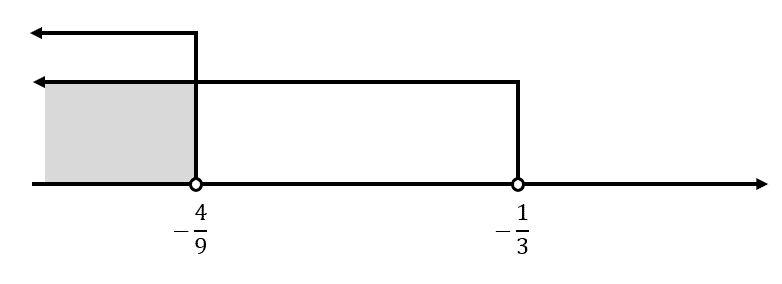
{S}_{12}=\left(-\infty , -\frac{4}{9}\right)
La solución general de la primera inecuación es:
{S}_{1}=\left(-\infty , -\frac{4}{9}\right)\cup \left(-\frac{1}{3}, \infty \right)
Inecuación 2.
\frac{1}{3x+1}<3\to \frac{1-9x-3}{3x+1}<0\to \frac{-2-9x}{3x+1}<0
La fracción será negativa cuando el numerador y el denominador tienen signos diferentes.
{S}_{21}:-2-9x>0 \mathrm{y}\mathrm{ }3x+1<0
{S}_{22}:-2-9x<0 \mathrm{y}\mathrm{ }3x+1>0
Resolvemos {S}_{21} :
-9x>2 \mathrm{y}\mathrm{ }3x<-1\to x<-\frac{2}{9} \mathrm{y}\mathrm{ }x<-\frac{1}{3}
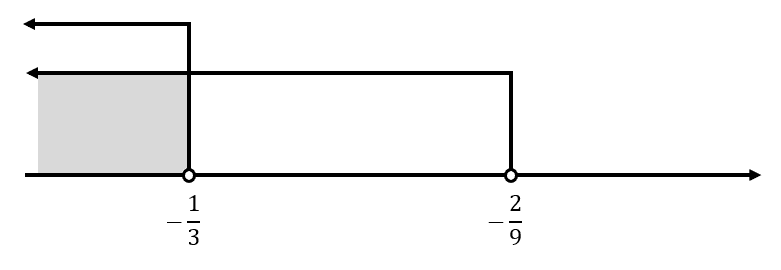
{S}_{21}=\left(-\infty , -\frac{1}{3}\right)
Resolvemos {S}_{22} :
-9x<2 \mathrm{y}\mathrm{ }3x>-1\to x>-\frac{2}{9} \mathrm{y}\mathrm{ }x>-\frac{1}{3}
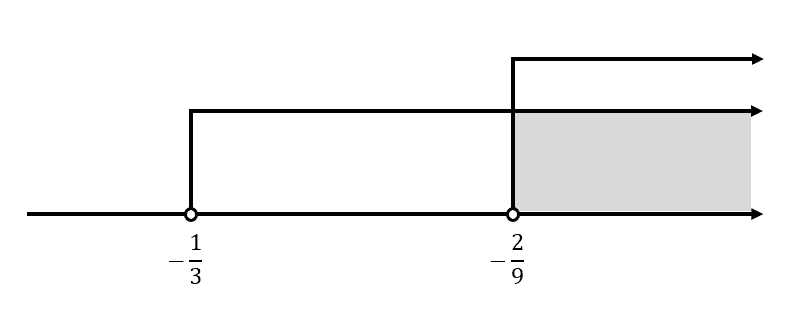
{S}_{22}=\left(-\frac{2}{9}, \infty \right)
El conjunto solución de la segunda inecuación es:
{S}_{2}=\left(-\infty , -\frac{1}{3}\right)\cup \left(-\frac{2}{9}, \infty \right)
Ahora, interceptamos ambas soluciones para hallar el conjunto de la inecuación original.
S={S}_{1}\cap {S}_{2}=\left[\left(-\infty , -\frac{4}{9}\right)\cup \left(-\frac{1}{3}, \infty \right)\right]\cap \left[\left(-\infty , -\frac{1}{3}\right)\cup \left(-\frac{2}{9}, \infty \right)\right]
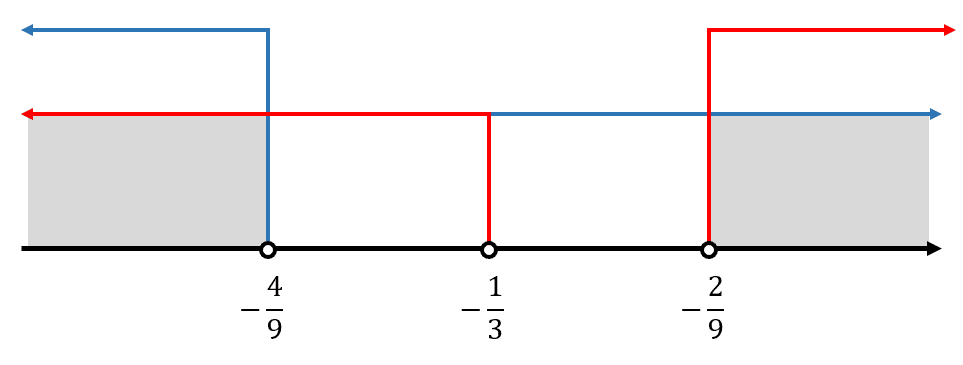
La intercepción entre los conjuntos ocurre en \left(-\infty , -\frac{4}{9}\right)\cup \left(-\frac{2}{9}, \infty \right) . Por tanto:
S=\left(-\infty , -\frac{4}{9}\right)\cup \left(-\frac{2}{9}, \infty \right)

La respuesta correcta es el inciso b).
Reactivo 33
Hallar el valor del siguiente límite:
\underset{x\to -4}{\mathrm{lim}}\frac{{x}^{2}-16}{x+4}
- 1
- -2
- 8
- -8
Solución:
Comenzamos evaluando el límite en el punto para comprobar la indeterminación.
\underset{x\to -4}{\mathrm{lim}}\frac{{x}^{2}-16}{x+4}=\frac{{\left(-4\right)}^{2}-16}{-4+4}=\frac{0}{0}
Tenemos una indeterminación 0/0. Factorizamos el numerador.
\underset{x\to -4}{\mathrm{lim}}\frac{{x}^{2}-16}{x+4}=\underset{x\to -4}{\mathrm{lim}}\frac{\left(x-4\right)\left(x+4\right)}{x+4}
Simplificamos y evaluamos.
\underset{x\to -4}{\mathrm{lim}}\left(x-4\right)=-4-4=-8
El límite de \frac{{x}^{2}-16}{x+4} cuando x tiende a -4 es -8.
La respuesta correcta es el inciso d).
Reactivo 34
Teniendo en cuenta la siguiente integral, ¿cuál de las siguientes expansiones en fracciones parciales del integrando permiten resolverla?
\int \frac{1}{x{\left(x-1\right)}^{2}}dx
- \frac{1}{x}+\frac{1}{x-1}+\frac{1}{{\left(x-1\right)}^{2}}
- \frac{1}{x}+\frac{1}{x-1}-\frac{1}{{\left(x-1\right)}^{2}}
- \frac{1}{x}-\frac{1}{x-1}+\frac{1}{{\left(x-1\right)}^{2}}
- \frac{1}{x}-\frac{1}{x-1}-\frac{1}{{\left(x-1\right)}^{2}}
Solución:
En este caso, debemos concentrarnos en aplicar fracciones parciales al integrando. El denominador tiene un factor lineal diferente x y a dos factores lineales repetidos {\left(x-1\right)}^{2}=\left(x-1\right)\left(x-1\right) . La descomposición quedaría:
\frac{1}{x{\left(x-1\right)}^{2}}=\frac{A}{x}+\frac{B}{x-1}+\frac{C}{{\left(x-1\right)}^{2}}
Pasamos a multiplicar el denominador de la izquierda hacia la derecha.
1=A{\left(x-1\right)}^{2}+Bx\left(x-1\right)+Cx
Desarrollamos y agrupamos.
1=A\left({x}^{2}-2x+1\right)+B\left({x}^{2}-x\right)+Cx
1=\left(A+B\right){x}^{2}+\left(-2A-B+C\right)x+A
Igualando coeficientes nos queda:
\begin{array}{c}A+B=0\\ -2A-B+C=0\\ A=1\end{array}
Resolviendo el sistema de ecuaciones nos queda:
A=1\to B=-1
C=2A+B\to C=2-1=1
Finalmente:
A=1, B=-1, C=1
Sustituyendo:
\frac{1}{x{\left(x-1\right)}^{2}}=\frac{1}{x}-\frac{1}{x-1}+\frac{1}{{\left(x-1\right)}^{2}}
La integral separada en fracciones parciales es:
\int \frac{1}{x{\left(x-1\right)}^{2}}dx=\int \frac{1}{x}dx-\int \frac{1}{x-1}dx+\int \frac{1}{{\left(x-1\right)}^{2}}dx
La respuesta correcta es el inciso c).
Reactivo 35
¿Cuál es el resultado de la siguiente integral?
\int \frac{\mathrm{ln}\left(1+x\right)}{x+1}dx
- \frac{1}{2}{\mathrm{ln}}^{2}\left(1+x\right)+C
- {\mathrm{ln}}^{2}\left(1+x\right)+C
- 2{\mathrm{ln}}^{2}\left(1+x\right)+C
- \frac{1}{2}{\mathrm{ln}}^{2}\left(1+x\right)+C
Solución:
Examinado la función integral, nos damos cuenta que no existe fórmula inmediata para resolverla; debemos emplear algún método. Ya que la derivada de \mathrm{ln}\left(1+x\right) es \frac{1}{x+1} , conviene aplicar cambio de variables.
u=\mathrm{ln}\left(1+x\right)\to du=\frac{1}{x+1}dx
Aplicando el cambio nos queda:
\int \frac{\mathrm{ln}\left(1+x\right)}{x+1}dx=\int udu
Resolvemos aplicando la fórmula de la integral de una potencia.
\int udu=\frac{1}{2}{u}^{2}+C
Devolvemos el cambio de variables.
\frac{1}{2}{u}^{2}+C\to \frac{1}{2}{\mathrm{ln}}^{2}\left(1+x\right)+C
Finalmente:
\int \frac{\mathrm{ln}\left(1+x\right)}{x+1}dx=\frac{1}{2}{\mathrm{ln}}^{2}\left(1+x\right)+C
Comparando con los incisos, concluimos que la respuesta correcta es el a).
Reactivo 36
Obtenga el resultado de calcular la siguiente integral definida:
{\int }_{1}^{2}\left(4x-1\right)dx
- 5
- -5
- 1
- 0
Solución:
Las integrales definidas se calculan a partir del segundo teorema fundamental del cálculo.
{\int }_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)
Donde F\left(b\right) y F\left(a\right) es la primitiva de f evaluada en los extremos de integración. Primero la integramos indefinidamente y a la función resultante la evaluamos en los extremos.
{\int }_{1}^{2}\left(4x-1\right)dx
Separamos en dos integrales.
{\int }_{1}^{2}\left(4x-1\right)dx=4{\int }_{1}^{2}xdx-{\int }_{1}^{2}dx
Aplicamos las fórmulas de la integral de x y del símbolo del diferencial respectivamente.
=4{\int }_{1}^{2}xdx-{\int }_{1}^{2}dx=\left.\begin{array}{c}\\ 2{x}^{2}-x\\ \end{array}\right]\begin{array}{c}2\\ \\ 1\end{array}=2{\left(2\right)}^{2}-2-\left[2{\left(1\right)}^{2}-1\right]=5
Finalmente:
{\int }_{1}^{2}\left(4x-1\right)dx=5
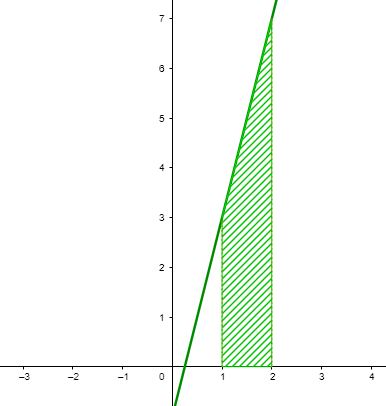
La respuesta correcta es el inciso a).
Reactivo 37
Calcule el resultado de la integral:
\int {\mathrm{tan}}^{2}xdx
- \mathrm{tan}x-x+C
- \mathrm{tan}x+x+C
- -\mathrm{tan}x-x+C
- \mathrm{tan}x+C
Solución:
Para resolver esta integral debemos emplear alguna sustitución trigonométrica.
\int {\mathrm{tan}}^{2}xdx=\int \frac{{\mathrm{sin}}^{2}x}{{\mathrm{cos}}^{2}x}dx
Aplicando la identidad pitagórica a {\mathrm{sin}}^{2}x=1-{\mathrm{cos}}^{2}x nos queda:
\int \frac{{\mathrm{sin}}^{2}x}{{\mathrm{cos}}^{2}x}dx=\int \frac{1-{\mathrm{cos}}^{2}x}{{\mathrm{cos}}^{2}x}dx=\int \left(\frac{1}{{\mathrm{cos}}^{2}x}-1\right)dx=\int {\mathrm{sec}}^{2}xdx-\int dx
Aplicamos la integral de la secante al cuadrado y la integral del diferencial.
\int {\mathrm{sec}}^{2}xdx-\int dx=\mathrm{tan}x-x+C
Finalmente:
\int {\mathrm{tan}}^{2}xdx=\mathrm{tan}x-x+C
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 38
Calcule la siguiente integral definida:
{\int }_{4}^{9}\frac{1-\sqrt{x}}{1+\sqrt{x}}dx
- 4\mathrm{ln}\frac{3}{4}+1
- 4\mathrm{ln}\frac{3}{4}-1
- 4\mathrm{ln}3-1
- 1-4\mathrm{ln}\frac{3}{4}
Solución:
Comenzamos a integrar indefinidamente. Debemos aplicar un cambio de variables algo ingenioso. Debido a que la x se encuentra dentro de una raíz cuadrada, el cambio será:
x={\left(z-1\right)}^{2}
De tal forma que:
dx=2\left(z-1\right)dz
Sustituimos todo en la integral:
{\int }_{4}^{9}\frac{1-\sqrt{x}}{1+\sqrt{x}}dx\to 2{\int }_{4}^{9}\frac{1-\sqrt{{\left(z-1\right)}^{2}}}{1+\sqrt{{\left(z-1\right)}^{2}}}\left(z-1\right)dz
Simplificamos:
2{\int }_{4}^{9}\frac{1-z+1}{1+z-1}\left(z-1\right)dz=2{\int }_{4}^{9}\frac{2-z}{z}\left(z-1\right)dz=2{\int }_{4}^{9}\frac{2-z}{z}\left(z-1\right)dz
2{\int }_{4}^{9}\frac{-{z}^{2}+3z-2}{z}dz=2{\int }_{4}^{9}\left(-z+3-\frac{2}{z}\right)dz
Separamos en tres integrales simples.
=2\left(-{\int }_{4}^{9}zdz+3{\int }_{4}^{9}dz-{\int }_{4}^{9}\frac{2}{z}dz\right)=2\left(-\frac{{z}^{2}}{2}+3z-2\mathrm{ln}z\right)\begin{array}{c}9\\ \\ 4\end{array}
2\left(-\frac{{z}^{2}}{2}+3z-2\mathrm{ln}z\right)\begin{array}{c}9\\ \\ 4\end{array}=\left.\begin{array}{c} \\ -{z}^{2}+6z-4\mathrm{ln}z\\ \end{array}\right]\begin{array}{c}9\\ \\ 4\end{array}
Devolvemos el cambio de variables.
z=1+\sqrt{x}
\left.\begin{array}{c} \\ -{z}^{2}+6z-4\mathrm{ln}z\\ \end{array}\right]\begin{array}{c}9\\ \\ 4\end{array}\to \left.\begin{array}{c} \\ -{\left(1+\sqrt{x}\right)}^{2}+6\left(1+\sqrt{x}\right)-4\mathrm{ln}\left(1+\sqrt{x}\right)\\ \end{array}\right]\begin{array}{c}9\\ \\ 4\end{array}
=-{\left(1+\sqrt{9}\right)}^{2}+6\left(1+\sqrt{9}\right)-4\mathrm{ln}\left(1+\sqrt{9}\right)-\left[-{\left(1+\sqrt{4}\right)}^{2}+6\left(1+\sqrt{4}\right)-4\mathrm{ln}\left(1+\sqrt{4}\right)\right]
=8-4\mathrm{ln}4-\left(9-4\mathrm{ln}3\right)=8-4\mathrm{ln}4-9+4\mathrm{ln}3=4\mathrm{ln}\frac{3}{4}-1
Finalmente:
{\int }_{4}^{9}\frac{1-\sqrt{x}}{1+\sqrt{x}}dx=4\mathrm{ln}\frac{3}{4}-1\approx -2.1507

La respuesta correcta es el inciso b).
Reactivo 39
Calcule se la siguiente integral indefinida:
\int x{e}^{2x}dx
- \frac{x}{2}-x{e}^{2x}+C
- \frac{x}{2}{e}^{2x}-\frac{x}{4}{e}^{2x}+C
- \frac{x}{2}{e}^{2x}-\frac{1}{4}{e}^{2x}+C
- \frac{x}{2}{e}^{2x}+\frac{1}{4}{e}^{2x}+C
Solución:
Analizando el integrando, queda claro que debemos aplicar el método de integración por partes. Debido a que la función exponencial queda invariante al integrar o derivarla, debemos seleccionar como u a la x .
u=x\to du=dx
dv={e}^{2x}dx\to v=\frac{1}{2}{e}^{2x}
Aplicando la fórmula de integración por partes:
\int x{e}^{2x}dx=\frac{x}{2}{e}^{2x}-\frac{1}{2}\int {e}^{2x}dx
La integral indicada se resuelve de forma inmediata aplicando la fórmula de la exponencial.
\frac{x}{2}{e}^{2x}-\frac{1}{2}\int {e}^{2x}dx=\frac{x}{2}{e}^{2x}-\frac{1}{4}{e}^{2x}+C
Finalmente:
\int x{e}^{2x}dx=\frac{x}{2}{e}^{2x}-\frac{1}{4}{e}^{2x}+C
Concluimos indicando como respuesta correcta al inciso c).
Reactivo 40
Calcule la siguiente integral indefinida:
\int \mathrm{sin}x{e}^{\mathrm{cos}x}dx
- -{e}^{\mathrm{cos}x}+C
- -{e}^{\mathrm{sin}x}+C
- {e}^{\mathrm{cos}x}+C
- -\mathrm{cos}x{e}^{\mathrm{cos}x}+C
Solución:
Para esta integral, debemos aplicar cambio de variables.
u=\mathrm{cos}x\to du=-\mathrm{sin}xdx
-du=\mathrm{sin}xdx
Implementando el cambio en la integral nos queda:
\int \mathrm{sin}x{e}^{\mathrm{cos}x}dx\to -\int {e}^{u}du
Esta integral se resuelve de forma inmediata con la fórmula de la exponencial.
-\int {e}^{u}du=-{e}^{u}+C
Devolvemos el cambio de variables.
-{e}^{u}+C\to -{e}^{\mathrm{cos}x}+C
Finalmente:
\int \mathrm{sin}x{e}^{\mathrm{cos}x}dx=-{e}^{\mathrm{cos}x}+C
Seleccionamos como respuesta correcta al inciso a).


