Llegamos a la quinta y última parte de la segunda versión del examen simulador de matemáticas para el área de Ingeniería y Ciencias Físico Matemáticas del Instituto Politécnico Nacional. Finalizamos resolviendo los ejercicios del 41 al 50.

¡Buen trabajo! Has llegado a la última parte del simulacro de matemáticas IPN.
Reactivo 41
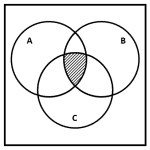
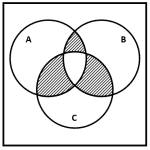
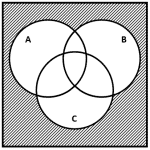
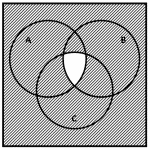
Dados los conjuntos A , B y C , ¿cuál de los siguientes diagramas de Venn representan la operación {\left(A\cup B\cup C\right)}^{c} ?
Solución:
En este caso, debemos identificar al diagrama que representa al complemento de la unión de los tres conjuntos. Primero recordemos qué significa la unión y el complemento de conjuntos.
La unión de dos o más conjuntos da como resultado a otro conjunto con los elementos de todos los operadores. Por otra parte, el complemento alude a todos los elementos que no pertenecen al conjunto respecto al universo U .
Vamos a dibujar la unión de los tres conjuntos, es decir, la región de A , B y C .
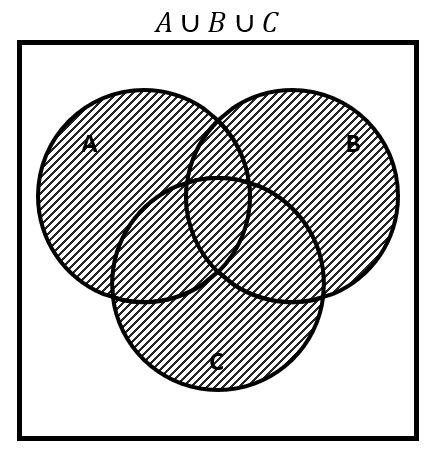
El complemento es la región fuera de la unión de los tres conjuntos.
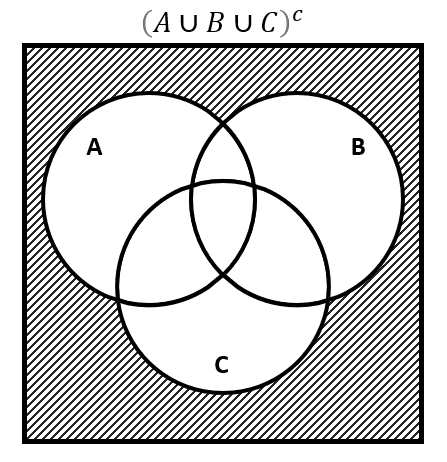
Comparando este resultado con los incisos, concluimos que la respuesta correcta es c).
Reactivo 42
Calcule la cantidad de cifras de 5 dígitos que se pueden escribir con los números 1, 2, 3, 4, 5, 6 teniendo en cuenta que se permite repetir.
- 7776
- 4555
- 2850
- 7876
Solución:
Para resolver cualquier problema de conteo (como el presente), debemos responder 3 preguntas:
- ¿Importa el orden de los elementos?
- ¿Intervienen todos los elementos?
- ¿Se permiten repeticiones?
¿Importa el orden de los elementos? Debido a que estamos formando cantidades numéricas, es claro que 12345 es diferente a 13245. Si importa el orden, tratamos con una variación/permutación.
¿Intervienen todos los elementos? El enunciado nos indica una lista de 6 elementos, pero las cifras son de 5 dígitos. No intervienen todos los elementos.
¿Se permiten repeticiones? De forma explícita, el enunciado establece la posibilidad de repetir elementos.
Se trata de una Variación con Repetición.
{VR}_{m}^{n}={m}^{n}
Para nosotros m=6 y n=5 . Sustituyendo y calculando:
{VR}_{6}^{5}={6}^{5}=7776
Se pueden crear 7776 cifras.
La respuesta correcta es el inciso a).
Reactivo 43
¿Cuántas cantidades menores a 3000 se pueden formar con los dígitos 2, 3, 4, 6 y 7?
- 85
- 125
- 120
- 155
Solución:
El enunciado establece que las cantidades deben ser menores a 3000 y, teniendo en cuenta que el menor dígito es “2” y que el mayor es “7”, el menor número que podemos formar es 2 y el mayor 2777.
Por otra parte, las cantidades menores a 3000 pueden tener 1, 2 y 3 cifras, por lo que el total de cantidades será la suma de las de 1, 2 y 3 cifras. Solo para aclarar, llegamos hasta 3 porque estas forman cantidades 2XXX, el 2 no cambia, permanece invariante.
Cantidades de 1 cifra.
{C}_{1}=5
Cantidades de 2 cifras. Como se permite repetir las calculamos como una variación con repetición:
{C}_{2}={5}^{2}=25
Cantidades de 3 cifras. Se calcula de la misma forma que en el paso anterior.
{C}_{3}={5}^{3}=125
Finalmente, el total de cantidades menores a 3000 es:
C={C}_{1}+{C}_{2}+{C}_{3}=5+25+125=155
Se pueden formar 155 cantidades menores a 3000 con los dígitos 2, 3, 4, 6 y 7.
La respuesta correcta es el inciso d).
Reactivo 44
En un experimento aleatorio, se tienen 2 urnas. La primera denotada como A, tiene 4 bolas rojas y 5 azules, mientras que la segunda llamada B posee 3 bolas rojas y 3 azules. Calcule la probabilidad de extraer una bola azul en el primer intento, considerando que no se permite la reposición.
- 0.7
- 0.5
- 0.533
- 0.6
Solución:
Aunque el enunciado sea largo y parezca complejo, debemos tener presente que la probabilidad de extraer una bola azul en el primer intento involucra a las bolas de ambas urnas, porque no se pide que sea de alguna urna específicamente.
Bolas en las urnas para la primera selección.
\mathrm{R}\mathrm{o}\mathrm{j}\mathrm{a}\mathrm{s}=4+3=7
\mathrm{A}\mathrm{z}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{s}=5+3=8
La probabilidad de extraer una azul se calcula como el cociente de bolas azules sobre el total de bolas.
P\left(A\right)=\frac{8}{8+7}=0.533
Hay una probabilidad de 0.533 de extraer una bola azul en el primer intento.
La respuesta correcta es el inciso c).
Reactivo 45
En un juego callejero, una persona tiene para seleccionar de una caja 4 tickets sin valor, 3 billetes de 100$ y 1 billete de 500$. La persona debe extraer 2 veces y se queda con el último ítem extraído. ¿Cuál es la probabilidad de sacar la tercera vez al billete de 500$?
- 0.25
- 0.125
- 0.5
- 0.1
Solución:
Debido a lo extenso del enunciado, realicemos el diagrama de árbol para visualizar mejor cómo se extraen los elementos y cómo cambian las probabilidades. En primer lugar, tenemos: 4 tickets 4t , 3 billetes de 100$ 3B100 y 1 billete de 500$ 1B500 .
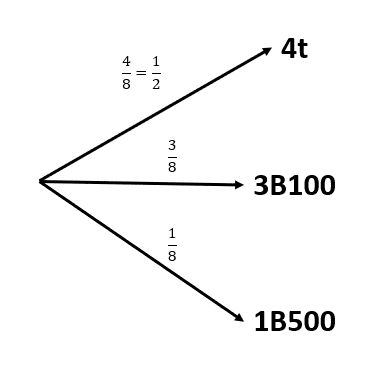
En la segunda extracción, solo nos interesan las probabilidades de sacar el billete de 500$ para 4t y 3B100 . Debido a que, si sacamos el de 500 en la primera, no lo ganaremos en la segunda.
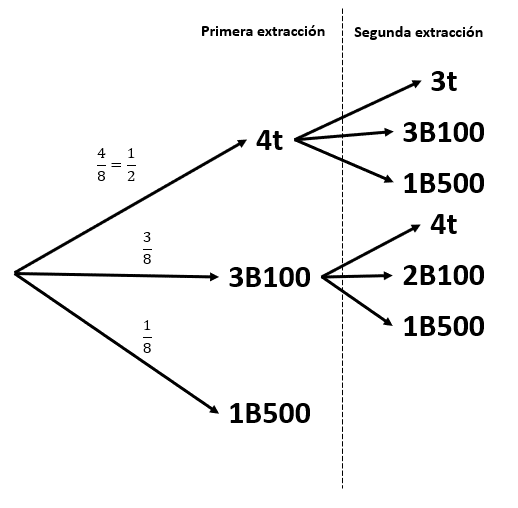
Si extraemos en la primera un ticket o un billete de 100$, tenemos cierta probabilidad de extraer el de 500$ para la segunda. Por esta razón, la probabilidad de sacar el de 500$ en la segunda, es la suma de: 4t\to 1B500 y 3B100\to 1B500 , por ser eventos mutuamente excluyentes.
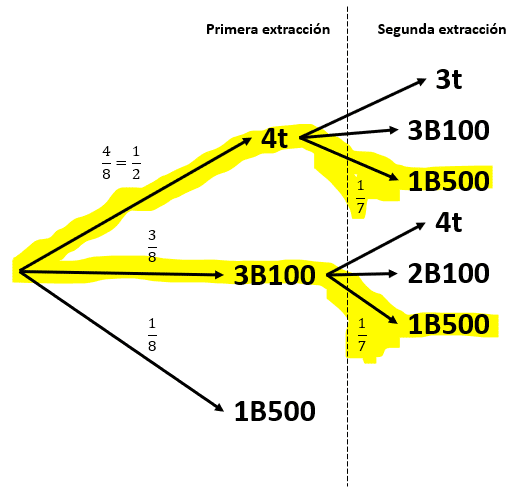
La probabilidad de cada evento por separado se calcula mediante la regla de la multiplicación.
P\left(4t\to 1B500\right)=\frac{1}{14}
P\left(3B500\to 1B500\right)=\frac{3}{56}
La probabilidad total se encuentra mediante la regla de la suma.
P\left(\to 1B500\right)=\frac{1}{14}+\frac{3}{56}=\frac{1}{8}=0.125
Comparando con los incisos, indicamos como correcto al b).
Reactivo 46
Dados los conjuntos A=\left\{a, b, c, d\right\} , B=\left\{b, c, f, g\right\} y U=\left\{a, b, c, d, e, f, g, h\right\} . Determine los elementos de {\left(A \mathrm{\Delta }\mathrm{ }B\right)}^{c} .
- \left\{b,c,e,h\right\}
- \left\{e,h\right\}
- \left\{b,c\right\}
- \left\{\varnothing \right\}
Solución:
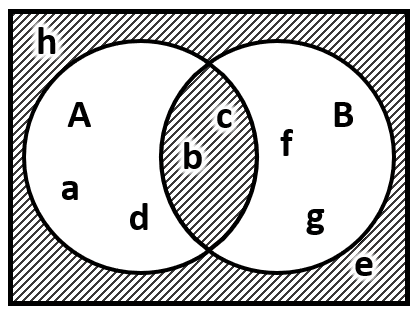
Comencemos por indicar que la operación entre A y B dentro del complemento se denomina diferencia simétrica y contiene a los elementos de A que no están en B junto a los elementos de B que no están en A. Gráficamente esta operación se representa como:
Examinando la figura, vemos que la diferencia simétrica es la diferencia entre unión de A y B y su intercepción.
A \mathrm{\Delta }\mathrm{ }B=\left(A\cup B\right)-\left(A\cap B\right)
Sustituimos a los conjuntos.
A \mathrm{\Delta }\mathrm{ }B=\left(\left\{a, b, c, d\right\}\cup \left\{b, c, f, g\right\}\right)-\left(\left\{a, b, c, d\right\}\cap \left\{b, c, f, g\right\}\right)
=\left\{a,b,c,d,f,g\right\}-\left\{b,c\right\}=\left\{a,d,f,g\right\}
Finalmente, a este resultado le aplicamos el complemento.
{\left(A \mathrm{\Delta }\mathrm{ }B\right)}^{c}={\left(\left\{a,d,f,g\right\}\right)}^{c}=\left\{b,c,e,h\right\}
Concluimos indicando como correcto al inciso a).
Reactivo 47
Un ejemplo de sucesos _______, es lanzar una moneda al aire dos veces. Por otro lado, serán _______ los sucesos de tomar agua y saciar la sed.
- Dependientes – independientes
- Independientes – dependientes
- Vacíos – independientes
- Iguales – dependientes
Solución:
En este caso, debemos completar el enunciado con las relaciones correctas entre los sucesos que se describen en las dos frases.
Un ejemplo de sucesos _______, es lanzar una moneda al aire dos veces.
El experimento de lanzar una moneda al aire, es independiente de lanzarla una segunda, tercera o enésima vez, ya que lanzar a la moneda en determinado momento no afectará de ninguna forma lanzarla de nuevo. La relación en este caso es: sucesos independientes.
Por otro lado, serán _______ los sucesos de tomar agua y saciar la sed.
De forma intuitiva, sabemos que tomar agua calmará la sed, en cualquier caso. Por ello, ambos eventos son compatibles. Las frases se completan de la siguiente manera:
Un ejemplo de sucesos independientes, es lanzar una moneda al aire dos veces. Por otro lado, serán dependientes los sucesos de tomar agua y saciar la sed.
La respuesta correcta es el inciso b).
Reactivo 48
Se tiene una fábrica de teclados mecánicos que dispone de dos líneas de ensamblaje A y B, de tal forma que elaboran el 60% y 40% de la producción total respectivamente. El porcentaje de teclados mal ensamblados de la línea A es del 2% mientras que el de la línea B es del 0.5%. Si un teclado es defectuoso, ¿cuál es la probabilidad de que haya sido fabricado por la línea A?
- 0.857
- 0.243
- 0.02
- 0.6
Solución:
El problema nos solicita calcular la probabilidad condicionada de que un teclado mecánico fabricado por la línea de producción A sea defectuoso, es decir: P\left(A|D\right) . Para ello, empleamos el teorema de Bayes.
P\left(A|D\right)=\frac{P\left(A\right)P\left(D|A\right)}{P\left(A\right)P\left(D|A\right)+P\left(B\right)P\left(D|B\right)}
Donde:
- P\left(A\right) es la probabilidad de que haya salido de la línea A
- P\left(D|A\right) es la probabilidad de que salga defectuoso un teclado de la línea A
- P\left(B\right) es la probabilidad de que haya salido de la línea B
- P\left(D|B\right) es la probabilidad de que salga defectuoso un teclado de la línea B
Examinando el enunciado, la probabilidad P\left(A\right) y P\left(B\right) son 0.6 y 0.4 respectivamente. Además, la probabilidad de que salga defectuoso un teclado de la línea A es P\left(D|A\right)=0.02 y para la línea B es P\left(D|B\right)=0.005 . Sustituimos en la ecuación del Teorema de Bayes:
P\left(A|B\right)=\frac{\left(0.6\right)\left(0.02\right)}{\left(0.6\right)\left(0.02\right)+\left(0.4\right)\left(0.005\right)}=0.857
La probabilidad de que un teclado mal ensamblado sea de la línea A es del 85.7%.
La respuesta correcta es el inciso a).
Reactivo 49
El valor que divide a un conjunto de datos en dos subconjuntos iguales lleva el nombre de…
- Desviación típica
- Media
- Mediana
- Moda
Solución:
Según la estadística descriptiva, el valor que separa en partes iguales a un conjunto de datos lleva el nombre de mediana. La respuesta correcta es el inciso c).
Reactivo 50
En un examen médico escolar se obtuvieron los siguientes datos:

Calcular la moda del conjunto.
- 58
- 62
- 64
- 66
Solución:
Para un conjunto de datos agrupados, la moda se calcula mediante la siguiente ecuación:
{M}_{o}={L}_{i}+\frac{{f}_{i}-{f}_{i-1}}{\left({f}_{i}-{f}_{i-1}\right)+\left({f}_{i}-{f}_{i+1}\right)}\cdot {a}_{i}
Donde:
- {f}_{i} es la mayor frecuencia absoluta del conjunto.
- {L}_{i} el extremo inferior de la clase modal.
- {a}_{i} amplitud de la clase.
- {f}_{i-1} la frecuencia absoluta de la clase anterior.
Examinando los datos, vemos que la frecuencia absoluta mayor es 15. Por tanto:
{f}_{i}=15, {L}_{i}=60, {a}_{i}=4, {f}_{i-1}=5, {f}_{i+1}=5
Sustituimos en la ecuación:
{M}_{o}=60+\frac{15-5}{\left(15-5\right)+\left(15-5\right)}\cdot 4=60+2=62
La moda del conjunto de datos es 62.
La respuesta correcta es el inciso b).