Seguimos con los reactivos del 21 al 30 del examen simulador de física para las carreras del área de ciencias médico biológicas del IPN.

Reactivo 21
Se dice que una propiedad física es extensiva si…
- No dependen de la cantidad de materia
- Dependen de la cantidad de materia
- Dependen del entrelazamiento entre las partículas fundamentales de la materia
- Dependen de los elementos de la materia
Solución:
Al estudiar las propiedades elementales de la materia, se suele hacer una distinción con base en cómo varían estas propiedades según cuánta materia tenemos.
Aquellas magnitudes que dependen de la cantidad de materia se denominan extensivas, las mismas pueden ser el volumen o la masa. Por otro lado, hay cantidades que permiten describir una característica del material sin importar cuánto de él tengamos, estas se denominan intensivas.
Teniendo en cuenta la definición anterior y comparando con las opciones, concluimos que la respuesta correcta es la b).
Se dice que una propiedad física es extensiva si depende de la cantidad de materia.
Reactivo 22
Si se aplica una fuerza de 40 N para calibrar un sensor de membrana con un área de 0.012 {\mathrm{m}}^{2} diseñada para medir presiones. Teóricamente ¿cuál debería ser la lectura del instrumento?
- 3333.33 \mathrm{P}\mathrm{a}
- 33.33 \mathrm{P}\mathrm{a}
- 333.33 \mathrm{P}\mathrm{a}
- 33333.3 \mathrm{P}\mathrm{a}
Solución:
Para resolver este problema, simplemente debemos emplear la relación entre fuerza y presión:
F=P\cdot A
Despejamos la presión:
P=\frac{F}{A}
Ahora, sustituimos en la ecuación los valores dados.
P=\frac{40 \mathrm{N}}{0.012 {\mathrm{m}}^{2}}=3333.33 \mathrm{P}\mathrm{a}
Seleccionamos como correcta la opción a).
Reactivo 23
Un ingeniero necesita diseñar las dimensiones de una prensa hidráulica para levantar vehículos de hasta 40000 kilogramos en el émbolo mayor, cuando se aplica una fuerza máxima de 100 Newtons en el émbolo de menor área.
¿Cuál debería ser la razón entre las áreas mayor y menor \frac{{A}_{M}}{{A}_{m}} ?
- 3920
- 4000
- 5920
- 2000
Solución:
Las prensas hidráulicas están basadas en el sencillo sistema de los vasos comunicantes, los cuales se encuentran rellenos de un líquido (el cual suele ser un aceite) y sus áreas transversales son distintas.
La transferencia de la fuerza ocurre debido a que la presión que ejerce sobre el líquido la placa menor se transfiere en igual magnitud hasta llegar a la placa mayor, donde la fuerza aplicada se amplifica.
{P}_{M}={P}_{m}\to \frac{{F}_{M}}{{A}_{M}}=\frac{{F}_{m}}{{A}_{m}}
Despejando áreas y fuerzas nos queda:
\frac{{A}_{m}}{{A}_{M}}=\frac{{F}_{m}}{{F}_{M}}
Ahora, sabemos cuál es la fuerza sobre el émbolo menor, {F}_{m}=100 \mathrm{N} pero debemos calcular la fuerza sobre el émbolo mayor aplicando la fórmula de peso.
{F}_{M}=Mg=\left(40000 \mathrm{k}\mathrm{g}\right)\left(9.8 \mathrm{m}/{\mathrm{s}}^{2}\right)=392000 \mathrm{N}
Sustituimos en la ecuación de áreas y fuerzas:
\frac{{A}_{m}}{{A}_{M}}=\frac{100}{392000}\to \frac{{A}_{M}}{{A}_{m}}=3920
La razón entre las áreas debe ser 3920.
Comparando con los incisos, concluimos que el correcto es a).
Reactivo 24
En un antiguo laboratorio de hidrodinámica, se emplea un manómetro en “U” para llevar a cabo los experimentos. Se ha conectado el manómetro a una tubería para medir el cambio de presión que experimenta el fluido al pasar por un agujero, tal como se muestra en la figura.
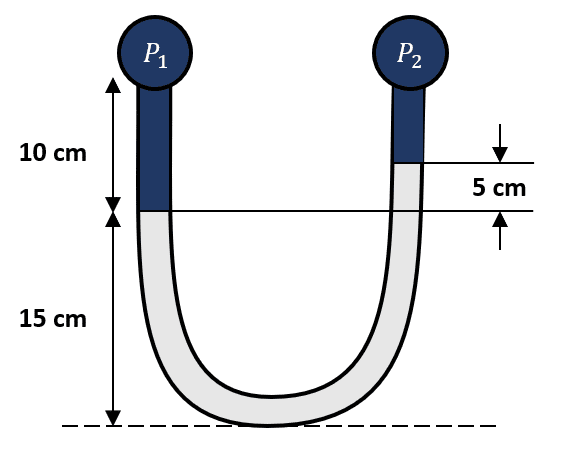
La sustancia gris en el manómetro es mercurio con peso específico igual a 13.6 \mathrm{N}/{\mathrm{m}}^{3} y el fluido de la tubería es agua con peso específico igual a 10 \mathrm{N}/{\mathrm{m}}^{3} . Calcule la diferencia de presión {P}_{1}-{P}_{2} .
- 16 Pa
- 17 Pa
- 18 Pa
- 19 Pa
Solución:
Para resolver este tipo de problemas, debemos aplicar la ley fundamental de la hidrostática:
{P}_{A}={P}_{B}+\gamma \mathrm{\Delta }h
Donde {P}_{A} es la presión en el punto bajo, {P}_{B} en el punto más alto, \gamma el peso específico de la sustancia y \mathrm{\Delta }h la diferencia de altura entre A y B . Debido a que la fórmula no puede aplicarse directamente, debemos establecer dos puntos en nuestro sistema: uno que será la referencia alta y otro la referencia alta. Examinando la figura, estos puntos pueden ser:
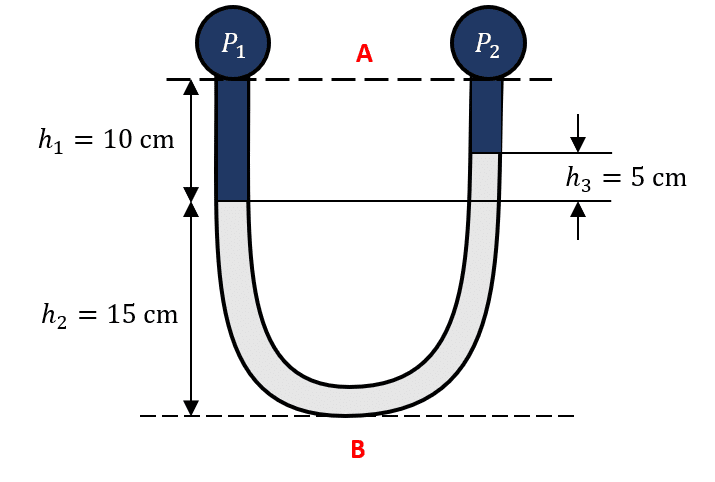
Ahora, lo que hacemos es encontrar la presión en el punto B desde {P}_{1} y luego desde {P}_{2} , para finalmente igualar las ecuaciones. Comenzamos con {P}_{1} :
{P}_{B}={P}_{1}+{\gamma }_{a}{h}_{1}+{\gamma }_{mg}{h}_{2}
Ahora vamos desde {P}_{2} .
{P}_{B}={P}_{2}+{\gamma }_{a}\left({h}_{1}-{h}_{3}\right)+{\gamma }_{mg}\left({h}_{3}+{h}_{2}\right)
Igualamos las ecuaciones:
{P}_{1}+{\gamma }_{a}{h}_{1}+{\gamma }_{mg}{h}_{2}={P}_{2}+{\gamma }_{a}\left({h}_{1}-{h}_{3}\right)+{\gamma }_{mg}\left({h}_{3}+{h}_{2}\right)
Pasamos al miembro de la izquierda {P}_{2} y el resto de términos a la derecha.
{P}_{1}-{P}_{2}={\gamma }_{a}{h}_{1}-{\gamma }_{a}{h}_{3}+{\gamma }_{mg}{h}_{3}+{\gamma }_{mg}{h}_{2}-{\gamma }_{a}{h}_{1}-{\gamma }_{mg}{h}_{2}
Simplificamos y agrupamos.
{P}_{1}-{P}_{2}={h}_{3}\left({\gamma }_{mg}-{\gamma }_{a}\right)
Sustituimos valores:
{P}_{1}-{P}_{2}=\left(0.05 \mathrm{m}\right)\left(13.6-10\right)=0.18 \mathrm{N}/{\mathrm{m}}^{2}
La presión diferencial entre los extremos del instrumento es de 0.18 Pascales.
Indicamos como respuesta correcta al inciso c).
Reactivo 25
Sobre un cuerpo de masa m se aplica una fuerza F que le permite ir del reposo a una velocidad v en un intervalo de tiempo t . Determine la expresión que permite determinar la fuerza que experimenta el cuerpo.
- F=-\frac{mv}{\mathrm{\Delta }t}
- F=\frac{m\mathrm{\Delta }t}{v}
- F=\frac{mv}{\mathrm{\Delta }t}
- F=\frac{\mathrm{\Delta }tv}{\mathrm{m}}
Solución:
Para resolver este problema, iniciamos planteando la segunda ley de Newton:
F=ma
Evidentemente, en su forma de valor absoluto. La masa del cuerpo es conocida, pero no su aceleración. Esta puede calcularse a partir de los datos suministrados sobre su cinemática:
a=\frac{{v}_{f}-{v}_{i}}{\mathrm{\Delta }t}
Sabemos que la velocidad inicial es cero y que la velocidad en \mathrm{\Delta }t es v .
a=\frac{v}{\mathrm{\Delta }t}
Sustituimos en la ecuación de fuerza.
F=\frac{mv}{\mathrm{\Delta }t}
Comparando con las opciones, concluimos que la correcta es la c).
Reactivo 26
Un coche parte del reposo e inicia un Movimiento Uniformemente Acelerado a razón de su velocidad de 6 \mathrm{m}/{\mathrm{s}}^{2} , el cuál mantiene durante 15 segundos. Finalizado este tiempo, aplica los frenos con una aceleración retardatriz de 8 \mathrm{m}/{\mathrm{s}}^{2} hasta detenerse. Calcule la distancia total recorrida.
- 1350 \mathrm{m}
- 675 \mathrm{m}
- 506.25 \mathrm{m}
- 1181.25 \mathrm{m}
Solución:
En este caso, tenemos el movimiento de un coche que tiene dos etapas bien establecidas por el enunciado, un primer MUA que mantiene durante 15 segundos, de tal forma que la velocidad final de esta primera etapa será la velocidad inicial de la segunda, un MUDA que mantiene hasta detenerse con una aceleración negativa (retardatriz) de 8 \mathrm{m}/{\mathrm{s}}^{2} .
Con el siguiente diagrama podemos expresar de forma sencilla lo antes descrito.
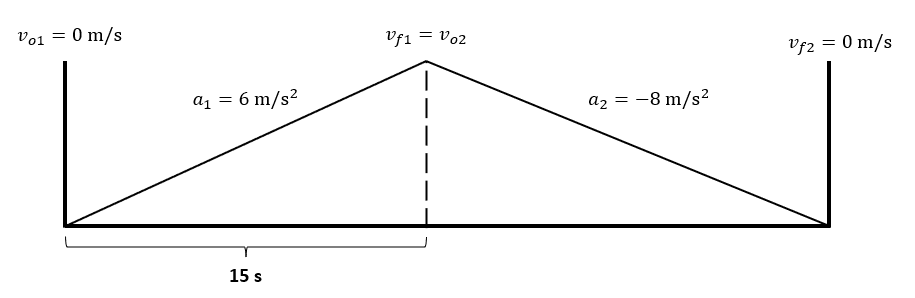
En este caso, lo que nos interesa calcular es la distancia recorrida en todo el movimiento, para ello, calcularemos la distancia 1 luego la 2 y el total será la suma de ambas.
{x}_{t}={x}_{1}+{x}_{2}
Primer movimiento.
Para la primera parte empleamos la ecuación:
{x}_{f1}={x}_{o1}+{v}_{o1}t+\frac{a{t}^{2}}{2}
Sustituyendo nos queda:
{x}_{f1}=0+\left(0\right)\left(15 \mathrm{s}\right)+\frac{\left(6\frac{\mathrm{m}}{{\mathrm{s}}^{2}}\right){\left(15 \mathrm{s}\right)}^{2}}{2}
{x}_{f1}=675 \mathrm{m}
Segundo movimiento.
Antes de comenzar, debemos calcular la velocidad final del movimiento anterior.
{v}_{f1}={v}_{o2}={v}_{o1}+{a}_{1}t=0+\left(6 \mathrm{m}/{\mathrm{s}}^{2}\right)\left(15 \mathrm{s}\right)
{v}_{f1}={v}_{o2}=90 \mathrm{m}/\mathrm{s}
Tenemos velocidad inicial, velocidad final y aceleración. Con esto podemos calcular el desplazamiento 2 con la ecuación:
{v}_{f2}^{2}={v}_{o2}^{2}+2{a}_{2}{x}_{2}
Despejamos {x}_{2} .
{x}_{2}=\frac{{v}_{f2}^{2}-{v}_{o2}^{2}}{2{a}_{2}}=\frac{0-{\left(90\frac{\mathrm{m}}{\mathrm{s}}\right)}^{2}}{2\left(-8\frac{\mathrm{m}}{{\mathrm{s}}^{2}}\right)}=506.25 \mathrm{m}
Finalmente, el desplazamiento total es de:
{x}_{t}=675+506.25=1181.25 \mathrm{m}
Comparando con los incisos, concluimos que la respuesta correcta está en d).
Reactivo 27
Calcule la presión que se experimenta en el fondo de una alberca, si tiene una profundidad máxima de 4 metros y está rellena de agua con una densidad promedio de 1000 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} . La presión atmosférica en el recinto de la alberca es de 100 kPa y suponga la gravedad igual a 10 \mathrm{m}/{\mathrm{s}}^{2} .
- 140 kPa
- 40 kPa
- 100 kPa
- 14 kPa
Solución:
Para resolver este problema, debemos emplear la ecuación de presión hidrostática:
{P}_{A}-{P}_{B}=\rho g\mathrm{\Delta }h
Donde {P}_{A} es la presión en el punto más bajo y {P}_{B} en el punto más alto del fluido que, para efectos de este problema, dicha presión es la atmosférica. Despejamos a la presión {P}_{A} y calculamos.
{P}_{A}={P}_{B}+\rho g\mathrm{\Delta }h
Sustituimos.
{P}_{A}=100 \mathrm{k}\mathrm{P}\mathrm{a}+\left(1000\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}\right)\left(10\frac{\mathrm{m}}{{\mathrm{s}}^{2}}\right)\left(4 \mathrm{m}\right)=100 \mathrm{k}\mathrm{P}\mathrm{a}+40\mathrm{ }\mathrm{k}\mathrm{P}\mathrm{a}
{P}_{A}=140 \mathrm{k}\mathrm{P}\mathrm{a}
La presión absoluta en el fondo de la alberca es de 140 kPa.
Concluimos indicando como correcta la opción a).
Reactivo 28
¿Cuál es el peso específico de una sustancia que ocupa un volumen de 0.04 metros cúbicos y pesa 5 Newtons?
- 100
- 115
- 120
- 125
Solución:
En este caso, simplemente debemos recordar la ecuación que nos permite calcular el peso específico de una sustancia:
\gamma =\rho \cdot g=\frac{m}{V}\cdot g=\frac{W}{V}
En este caso, tenemos tanto el volumen como el peso W de la sustancia, solo nos queda sustituir.
\gamma =\frac{5 \mathrm{N}}{0.04 {\mathrm{m}}^{3}}=125\frac{\mathrm{N}}{{\mathrm{m}}^{3}}
La respuesta correcta es el inciso d).
Reactivo 29
La ecuación de continuidad de un fluido que circula a través de una tubería que cambia de sección transversal entre un punto 1 y un punto 2, establece que…
- Los caudales cambian según la diferencia de sus secciones
- Los caudales cambian según la razón de sus secciones
- Los caudales permanecen constantes para ambos puntos
- Los caudales cambian de forma no Newtoniana
Solución:
De forma general, las ecuaciones de continuidad suelen establecer la igualdad respecto a una variable de un sistema físico que permanece constante luego de que el sistema o una parte de él sufre alguna transformación.
En mecánica de fluidos tenemos principalmente dos ecuaciones de continuidad a la hora de trabajar con sustancias: conservación de la masa y conservación del caudal, aunque con algunas transformaciones matemáticas ambas relaciones son equivalentes.
En este caso nos interesa la continuidad del caudal, ya que el enunciado hace referencia a un fluido que se desplaza a lo largo de una tubería que cambia de sección transversal.
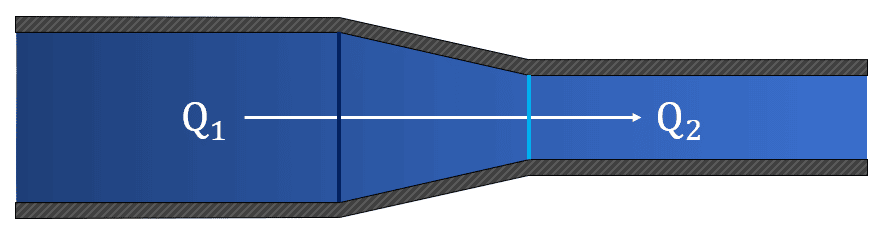
Debido a que el flujo no se ramifica de forma externa, es decir, no existe pérdida de flujo, a pesar de la caída en la sección transversal lo que pasa por el punto 1 pasa también por el punto 2, por tanto:
{Q}_{1}={Q}_{2}
Los caudales se mantienen.
Teniendo en cuenta este análisis y comparando con los incisos, concluimos que la respuesta correcta está en c).
Reactivo 30
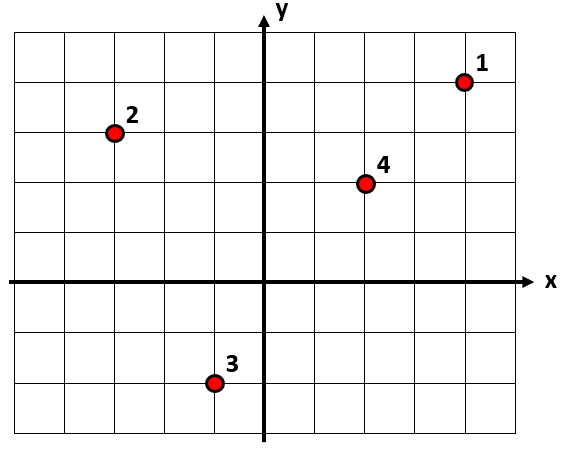
A partir del siguiente sistema de partículas, identifique la opción en la que se representa el centro de masas. Tenga en cuenta que la masa de las partículas es: {m}_{1}={m}_{3}=1 \mathrm{k}\mathrm{g} y {m}_{2}={m}_{4}=1.5 \mathrm{k}\mathrm{g} y que la distancia entre cuadros es de 1 unidad.
- \left(-0.3, -1.9\right)
- \left(-0.3, 1.9\right)
- \left(0.3, -1.9\right)
- \left(0.3, 1.9\right)
Solución:
Antes de pasar a escribir la ecuación para calcular el centro de masas del sistema, debemos identificar las coordenadas de cada partícula a partir de la figura.
{P}_{1}=\left(4, 4\right), {P}_{2}=\left(-3, 3\right), {P}_{3}=\left(-1, -2\right), {P}_{4}=\left(2, 2\right)
Ahora, las coordenadas del centro de masas son:
{X}_{c}=\frac{\sum {m}_{i}{x}_{i}}{\sum {m}_{i}}, {Y}_{c}=\frac{\sum {m}_{i}{y}_{i}}{\sum {m}_{i}}
Debido a que tenemos 4 partículas, la ecuación queda como:
{X}_{c}=\frac{{m}_{1}{x}_{1}+{m}_{2}{x}_{2}+{m}_{3}{x}_{3}+{m}_{4}{x}_{4}}{{m}_{1}+{m}_{2}+{m}_{3}+{m}_{4}}
{Y}_{c}=\frac{{m}_{1}{y}_{1}+{m}_{2}{y}_{2}+{m}_{3}{y}_{3}+{m}_{4}{y}_{4}}{{m}_{1}+{m}_{2}+{m}_{3}+{m}_{4}}
Sustituyendo los valores:
{X}_{c}=\frac{\left(1\right)\left(4\right)+\left(1.5\right)\left(-3\right)+\left(1\right)\left(-1\right)+\left(1.5\right)\left(2\right)}{1+1.5+1+1.5}=0.3 \mathrm{m}
{Y}_{c}=\frac{\left(1\right)\left(4\right)+\left(1.5\right)\left(3\right)+\left(1\right)\left(-2\right)+\left(1.5\right)\left(2\right)}{1+1.5+1+1.5}=1.9 \mathrm{m}
Las coordenadas del centro de masas son:
CM=\left(0.3, 1.9\right)
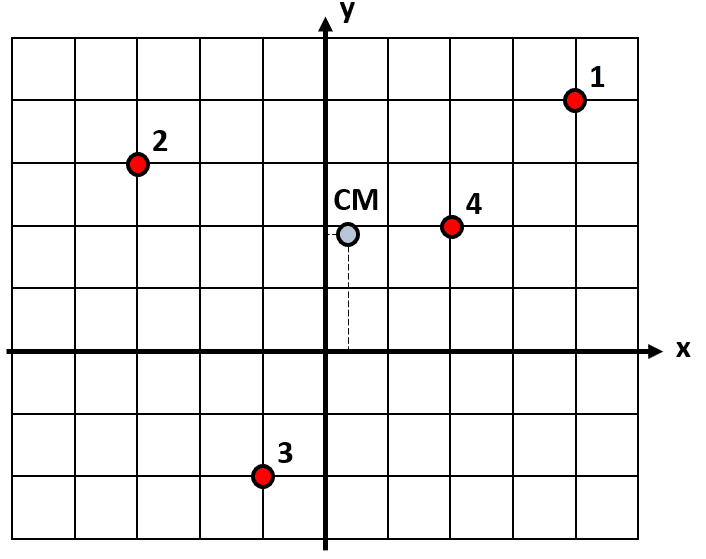
Concluimos que la respuesta correcta es el inciso d).


