¡Hola de nuevo aspirante! En este post vamos a resolver los ejercicios del 31 al 40, correspondientes a la cuarta parte del simulacro de física para el examen de ingreso al IPN en el área de Ciencias Médico Biológicas.

Continuamos con los siguientes 10 reactivos del simulacro de física, de cara a la prueba de ingreso del Instituto Politécnico Nacional en el área de las Ciencias Médico Biológicas.
Recuerda resolver los reactivos por tu cuenta antes de revisar la respuesta. Además, checa el temario y estudia los fundamentos de cada uno. Recuerda que no importa la cantidad de reactivos que resuelvas, sino, tu capacidad de análisis ante cada problema.
Reactivo 31
¿Cuál es el volumen final en litros, de un sistema isobárico cilindro y pistón que pasa de tener una temperatura de 135 K a 235 K, con un volumen inicial de 0.01 metros cúbicos?
- 20 l
- 4 l
- 15 l
- 56 l
Solución:
Para resolver este problema, debemos utilizar una de las variantes de la ley de los gases ideales, específicamente, aquella que relaciona el volumen y la temperatura en dos momentos distintos para un gas.
Ley de Charles.
\frac{{V}_{1}}{{T}_{1}}=\frac{{V}_{2}}{{T}_{2}}
Despejamos el volumen en el estado 2 del proceso.
{V}_{2}=\frac{{T}_{2}}{{T}_{1}}\cdot {V}_{1}
Sustituimos los valores dados. Recuerda que la temperatura debe estar en Kelvin y el volumen en metros cúbicos.
{V}_{2}=\frac{235 \mathrm{K}}{135 \mathrm{K}}\cdot 0.01 {\mathrm{m}}^{3}=0.0174 {\mathrm{m}}^{3}
Ahora, convertimos este resultado a litros con la relación: 1 {\mathrm{m}}^{3}=1000 \mathrm{l} .
0.0174 {\mathrm{m}}^{3}\cdot \frac{1000 \mathrm{l}}{1 {\mathrm{m}}^{3}}=17.4 \mathrm{l}
El volumen final es de 17.4 litros.
La respuesta correcta es el inciso b).
Reactivo 32
En un proceso termodinámico a volumen constante, ¿cómo se calcula el trabajo cuando incrementa la temperatura?
- No se efectúa trabajo
- A través del calor irradiado
- A través del cambio de energía interna
- A través de la eficiencia del sistema
Solución:
Recordemos que el trabajo es una cantidad física escalar que se calcula como el producto de la fuerza aplicada sobre un cuerpo por el desplazamiento que este ha sufrido (de una forma bastante simplificada).
W=F\cdot \mathrm{\Delta }x
Si extendemos esta idea a cualquier proceso de la naturaleza, llegaremos a la conclusión de que se genera o produce trabajo cuando hay desplazamiento de frontera en un sistema.
Ahora, teniendo en cuenta el hipotético sistema del enunciado, si el proceso es isocórico no hay desplazamiento de frontera, por ende, no se genera trabajo. Concluimos que la respuesta correcta es el inciso a).
Reactivo 33
¿Cuál es la temperatura en Celsius, de un termómetro que registra 78 F?
- 35°
- 7°
- 20°
- 55°
Solución:
Para convertir temperaturas Fahrenheit a Celsius, tenemos la siguiente ecuación.
{T}_{c}=\frac{5}{9}\left({T}_{F}-{32}^{°}\right)
Sustituimos la temperatura dada.
{T}_{c}=\frac{5}{9}\left(78°-{32}^{°}\right)=25.55°
La temperatura en Celsius es de 25.55°
La respuesta correcta es el inciso d).
Reactivo 34
¿Cuál es la relación entre las velocidades de las ondas que se propagan por una cuerda A cuya densidad lineal es 2 veces mayor a la de otra cuerda B?
- {v}_{B}=\sqrt{2}{v}_{A}
- {v}_{B}=\frac{{v}_{A}}{\sqrt{2}}
- {v}_{B}=4{v}_{A}
- {v}_{B}=2{v}_{A}
Solución:
Recordemos que la ecuación para calcular la velocidad de una onda a través de una cuerda es:
v=\sqrt{\frac{T}{\mu }}
Donde T es la tensión en la cuerda y \mu su densidad lineal. Para efectos del problema, supondremos que ambas cuerdas tienen la misma tensión, en caso contrario no tiene sentido hacer la comparación.
Para la cuerda A:
{v}_{A}=\sqrt{\frac{T}{{\mu }_{A}}}=\sqrt{\frac{T}{2{\mu }_{B}}}
Para la cuerda B:
{v}_{B}=\sqrt{\frac{T}{{\mu }_{B}}}
Hacemos el cociente {v}_{A}/{v}_{B} .
\frac{{v}_{A}}{{v}_{B}}=\frac{\sqrt{\frac{T}{2{\mu }_{B}}}}{\sqrt{\frac{T}{{\mu }_{B}}}}=\frac{\sqrt{{\mu }_{B}}}{\sqrt{2{\mu }_{B}}}=\frac{1}{\sqrt{2}}
Finalmente:
{v}_{B}=\sqrt{2}{v}_{A}
La velocidad de las ondas en la cuerda B es \sqrt{2} veces mayor (ya que \sqrt{2}>1 ) que la velocidad en la cuerda A.
La respuesta correcta es la a).
Reactivo 35
Las ondas sonoras que se propagan por el aire se clasifican como:
- Transversales
- Polarizadas
- Longitudinales
- Dispersas
Solución:
Comencemos recordando que las ondas sonoras se originan debido a un cambio de presión en determinada parte del espacio y, como ya sabemos, dicha fuente puede ser un altavoz, nuestra voz o el sonido que hacemos al escribir en nuestro teclado.
Debido a que el aire se comporta como un fluido, podemos imaginar que las partículas que lo conforman están comunicadas mecánicamente entre ellas por pequeños muelles, de tal forma que cuando una de ellas es perturbada, propaga la perturbación a través de la red de partículas.
Teniendo en cuenta la forma en que se contagia la perturbación, sabemos que las partículas “vibran” a lo largo de la dirección de propagación. Esta es la característica fundamental de las ondas longitudinales.
Indicamos como respuesta correcta al inciso c).
Reactivo 36
El trabajo que realiza un ciclo termodinámico real con una eficiencia del 45%, si el mismo absorbe 4000 Joules de calor.
- 1800 J
- 2200 J
- 3250 J
- 750 J
Solución:
La eficiencia termodinámica de cualquier proceso termodinámico puede calcularse como el cociente entre el trabajo realizado por el proceso entre el calor absorbido.
n=\frac{{W}_{neto}}{{Q}_{abs}}
Despejamos el trabajo neto de la ecuación:
{W}_{neto}=n\cdot {Q}_{abs}=\left(0.45\right)\left(4000 \mathrm{J}\right)=1800 \mathrm{J}
El ciclo es capaz de general 1800 Joules de trabajo.
La respuesta correcta es el inciso a).
Reactivo 37
Un sistema cilindro y pistón efectúa un proceso isobárico a 235 kPa. Si la diferencia de volumen entre los estados inicial y final es de 15 litros, calcule el trabajo mecánico total.
- 3525 J
- 4325 J
- -3525 J
- 0 J
Solución:
En los procesos termodinámicos donde ocurre un desplazamiento de la frontera, se dice que el sistema o sobre él se efectúa trabajo mecánico. Ahora, según el tipo de proceso se emplea una u otra ecuación para la estimación del trabajo.
Debido a que el proceso es a presión constante, la ecuación es:
W=P\left({V}_{2}-{V}_{1}\right)
No tenemos el volumen en cada caso, pero si la diferencia {V}_{2}-{V}_{1}=15 \mathrm{l} , debemos convertirla a metros cúbicos.
{V}_{2}-{V}_{1}=15 \mathrm{l}\cdot \frac{0.001 {\mathrm{m}}^{3}}{1 \mathrm{l}}=0.015 {\mathrm{m}}^{3}
Sustituimos finalmente en la ecuación.
W=235000\frac{\mathrm{N}}{{\mathrm{m}}^{2}}\cdot 0.015 {\mathrm{m}}^{3}=3525 \mathrm{J}
El sistema genera 3525 Joules de trabajo.
La respuesta correcta es la opción a).
Reactivo 38
En el laboratorio de acústica de una universidad, se está realizando un experimento para comprobar cómo varía la velocidad del sonido en función del medio en el que se propaga. Si la densidad del segundo medio es 4 veces mayor que la del primer medio, ¿cuál es la relación entre las velocidades de propagación? Asuma que los medios se comportan como gases ideales.
- {v}_{1}=2{v}_{2}
- {v}_{1}=\frac{{v}_{2}}{2}
- {v}_{1}=3{v}_{2}
- {v}_{1}={v}_{2}
Solución:
Para resolver este problema, debemos partir recordando la ecuación de la velocidad del sonido en gases considerados ideales:
v=\sqrt{\frac{\gamma P}{\rho }}
Donde \gamma es la constante de dilatación adiabática, P es la presión del gas y \rho es su densidad. Consideramos que la constante de dilatación y la presión son iguales. Las velocidades en los medios son:
{v}_{1}=\sqrt{\frac{\gamma P}{{\rho }_{1}}}
{v}_{2}=\sqrt{\frac{\gamma P}{{\rho }_{2}}}=\sqrt{\frac{\gamma P}{4{\rho }_{1}}}=\frac{1}{2}\sqrt{\frac{\gamma P}{{\rho }_{1}}}
Dividimos ambas expresiones:
\frac{{v}_{1}}{{v}_{2}}=\frac{\sqrt{\frac{\gamma P}{{\rho }_{1}}}}{\frac{1}{2}\sqrt{\frac{\gamma P}{{\rho }_{1}}}}=2
Concluimos entonces que:
{v}_{1}=2{v}_{2}
La velocidad del medio 1 es el doble que en el medio 2.
La respuesta correcta es el inciso a).
Reactivo 39
Calcule la longitud de onda de la nota musical la si su velocidad de propagación es de 340 \mathrm{m}/\mathrm{s} en el aire y tiene una frecuencia de 440 Hz.
- 1.3 \mathrm{m}
- 7.73 \mathrm{m}
- 3.27 \mathrm{m}
- 0.773 \mathrm{m}
Solución:
En este caso, empleamos la ecuación que relaciona la longitud de onda, la frecuencia y la velocidad de propagación de una onda:
v=f\cdot \lambda
Despejamos la longitud de onda y calculamos.
\lambda =\frac{v}{f}=\frac{340 \mathrm{m}/\mathrm{s}}{440 \mathrm{H}\mathrm{z}}=0.773 \mathrm{m}
La longitud de onda de la nota musical la es de 0.773 metros.
La respuesta correcta está en el inciso d).
Reactivo 40
A partir de las leyes fundamentales de la electroestática, indique cuál de las siguientes imágenes ejemplifica un evento imposible.
Solución:
Para encontrar la imagen que ejemplifica un evento imposible según la electroestática, vayamos analizando una a una comprobando que fenómeno está representando.
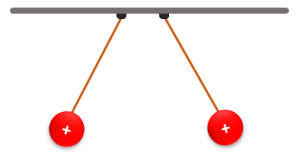
Imagen A.

Tenemos a dos cargas eléctricas del mismo signo, colgadas de un hilo y que aparentan repelerse una con la otra. Este resultado, según la electrostática es correcto. Lo mismo pasa con la Imagen B ya que en ella vemos a dos cargas opuestas que se atraen mutuamente.

Ambas situaciones son correctas.
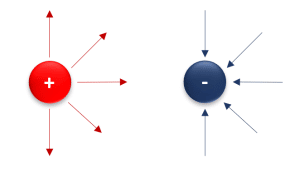
Imagen C.
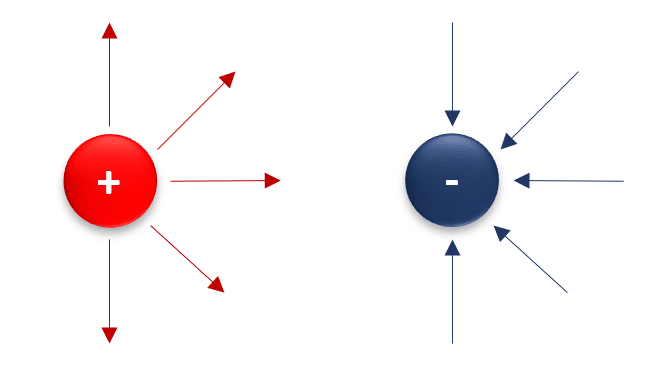
En esta figura, se muestra la dirección en la que apuntan las líneas de fuerza para las cargas positivas y negativas. Parte de los resultados de la electrostática, es que las líneas de campo salen perpendicularmente de las cargas positivas y convergen (entran) de la misma forma hacia las cargas negativas.
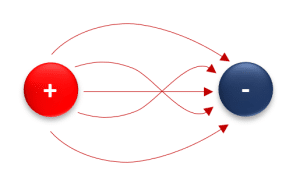
Imagen D.
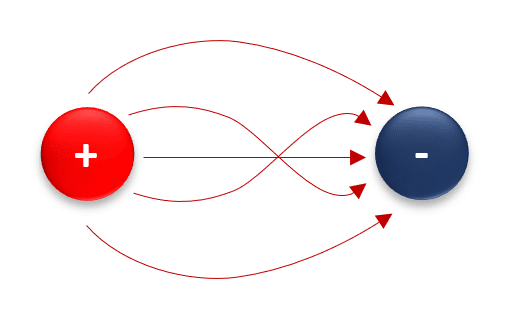
Acá sí que notamos una representación incorrecta de las líneas de campo que salen de una carga positiva y entran a otra negativa. Si bien el sentido es correcto, el recorrido de las líneas de fuerza no lo es, ya que, éstas nunca se cruzan.
Concluimos que la respuesta correcta es el inciso d).