Si has llegado hasta la última parte de nuestra guía, ¡Felicidades! Estamos seguros de que todo este esfuerzo en el cual estás invirtiendo tu tiempo, dará frutos. En vista de ello, te invitamos a enfocarte ahora en acabar con los últimos ejercicios de nuestra guía resuelta de Razonamiento Matemático del IPN.
La intención de estos post es que seas capaz de tener orientación para resolver los 50 ejercicios de Razonamiento Matemático de la guía del IPN.
Como has notado, decidimos segmentar esta guía de ejercicios resueltos en varias partes. En este caso, te encuentras frente a la última parte de ella, en la cual nos dedicaremos a abordar los ejercicios que van del número 41 al 50. ¡Continúa leyendo!
¿Qué viene en el examen del IPN?
El Instituto Politécnico Nacional, a través de su proceso de admisión, evalúa a sus aspirantes en un examen compuesto de 130 preguntas. Este examen se divide en dos partes, donde la primera aborda preguntas de matemática y comunicación, mientras que la segunda se enfoca en Física, Química y Biología.
Ten en cuenta también que la duración de este examen es de dos horas y media, así que debes estar preparado. En este sentido, para que puedas tener una visión más clara de lo que encontrarás en este examen, aquí tienes la cantidad de preguntas de cada área en la cual serás evaluado:
- 50 preguntas de matemáticas.
- 40 preguntas de comunicación.
- 10 preguntas de biología.
- 15 preguntas de química.
- 15 preguntas de física.
Ya no queda más que añadir, ¡Te invitamos a prepararte en esta quinta y última parte de nuestra guía resuelta de ejercicios de Razonamiento Matemático del IPN:
Conoce el curso que cubre todos los temas del nuevo examen de ingreso al IPN con clases en vivo y exámenes simulacro.
Reactivo 41: Problemas matemáticos
El último recibo de luz de un usuario indica que consumió 480 kWh. Si el precio por kWh tiene tres valores:
Básico: Se aplica de 0 a 150 kWh y cuesta $1 por cada kWh.
Intermedio: Va de 151 a 450 kWh y cuesta $2 por cada kWh.
Excedente: Va de 451 kWh en adelante y cuesta $3 por kWh.
¿Cuántos pesos pagó el usuario?
- 810
- 820
- 840
- 860
Solución:
Ya que la factura del usuario fue de 480 kWh, tuvo consumo en los tres rangos de precios. Del básico consumió los 150 kWh completos, que multiplicando por la tasa \frac{1 \$}{k W h} da un total de $150.
Del rango intermedio consumió 300 kWh, es decir 450-151+1=300 \mathrm{kWh} . Se debe sumar 1 porque si solo se realiza la resta no estaríamos considerando uno de los topes en el rango 151-450 kWh. Ya que el consumo fue de 300 kWh y la tarifa de \frac{2 \$}{k W h} , el total es de $600.
Por último, quedan 480-150-300=30 k W h que entran en el rango de Excedente cuya tarifa es \frac{3 \$}{k W h} , arrojando un total de $90. Si sumamos todo, obtenemos que el total de la cuenta en pesos es:
\text { Pago }=\$ 150+\$ 600+\$ 90=\$ 840
Comparando con las opciones, la respuesta correcta es la c).
Reactivo 42: Problemas matemáticos
¿Cuántos cubos de 5 cm por lado caben en un cubo de 1 \mathrm{~m}^{3} ?
- 4000
- 6000
- 8000
- 10000
Solución:
Para determinar la cantidad de cubos que caben dentro de otro con un volumen de 1 metro cúbico, debemos calcular el volumen que tiene uno de los cubos más pequeños y luego dividir 1 metro cúbico por dicho volumen, el resultado será la cantidad solicitada.
Ya que es un cubo, el volumen del mismo se obtiene como:
V_{c}=a^{3}
Donde a es la longitud de las aristas del cubo. Antes de sustituir en la ecuación, pasemos los 5 cm a metros para tener unidades homogéneas, ya que el volumen del cubo grande está en metros cúbicos.
5 \mathrm{~cm}=0.05 \mathrm{~m}
Sustituimos en la ecuación de volumen.
V_{c}=(0.05 \mathrm{~m})^{3}=0.000125 \mathrm{~m}^{3}
La cantidad de cubos que entran en 1 metro cúbico es:
N^{\circ} \mathrm{cubos}=\frac{1 \mathrm{~m}^{3}}{0.000125 \mathrm{~m}^{3}}=8000 \mathrm{cubos}
Comparando con las opciones del problema, la respuesta correcta es la c).
Reactivo 43: Operaciones algebraicas
Hallar el valor de x en la expresión \sqrt{2 x+y}=3 , considerando que y=5 .
- 1
- 2
- 5
- 7
Solución:
En este caso, sustituimos en la expresión el valor de y y despejamos a x .
\sqrt{2 x+y}=3, \text { si } y=5 \text { entonces: } \sqrt{2 x+5}=3
Elevamos al cuadrado para eliminar la raíz.
(\sqrt{2 x+5})^{2}=3^{2}
2 x+5=9
Simplificamos y obtenemos el valor de x .
2 x=4
\therefore x=2
Comparando con las opciones, la respuesta correcta es la b).
Reactivo 44: Problemas matemáticos
El perímetro de un rectángulo es de 128 cm y la diferencia entre las medidas de su base y su altura es de 12 cm. Calcular las dimensiones de dicho rectángulo.
- Base 24, altura 12
- Base 26, altura 38
- Base 30, altura 18
- Base 40, altura 28
Solución:
Ya que la figura es un rectángulo, tanto su altura como su base son diferentes. Llamaremos a la altura h y a la base b .
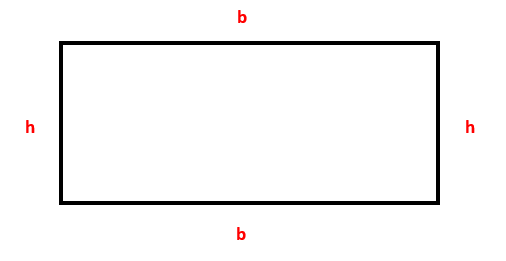
De la imagen, podemos extraer que el perímetro del rectángulo se calcula como:
2 h+2 b=128
Además, el enunciado dice que la diferencia entre la base y la altura es 12 cm. Como no se indica con exactitud quien se resta con quien, lo correcto sería expresarlo en forma de valor absoluto:
|h-b|=12
Pero esto complicaría innecesariamente el problema, asumamos que la diferencia es h-b , si los resultados dan cambiados respecto de la respuesta, es porque la diferencia era en sentido contrario.
h-b=12
Con estas dos ecuaciones, obtenemos un sistema de ecuaciones lineales 2×2, que puede ser resuelto por cualquier método. Nosotros emplearemos el método por sustitución. De la segunda ecuación despejamos a la altura y la sustituimos en la primera ecuación.
h=12+b \rightarrow 2(12+b)+2 b=128
4 b+24=128
Despejamos el valor de la base.
4 b=104 \rightarrow b=26
Este valor de base lo sustituimos en la ecuación más conveniente para calcular la altura.
h=12+b \rightarrow h=12+26=38
Concluimos entonces que la base mide 26 cm y la altura 38 cm.
Comparando con las opciones del problema, la respuesta correcta es la b).
Reactivo 45: Lenguaje algebraico y lenguaje natural
¿Qué expresión representa el siguiente enunciado?
A un número multiplicado por 5 se le añade 6 y a la suma obtenida se le multiplica 4, se le suma 9 al nuevo producto y el resultado se multiplica por 5.
- \{4[(5 x+6)+9]\} 5
- 5[4(5 x+6+9)]
- [5(5 x+6) 4+9]
- [4(5 x+6)+9] 5
Solución:
Para dar con la expresión correcta, debemos analizar la frase por trozos e identificar así las operaciones correspondientes. Recordemos que, cuando se dicen cosas como: un número, una cantidad o similares, nos referimos a una variable.
Comencemos por A un número multiplicado por 5 se le añade 6… Un número hace alusión a la variable x , luego a esta se le multiplica por 5 y al resultado se le suman 6 unidades.
5 x+6
Ahora …y a la suma obtenida se le multiplica 4. Al resultado anterior se le debe multiplicar por 4.
4(5 x+6)
Por último …se le suma 9 al nuevo producto y el resultado se multiplica por 5. A la expresión anterior le sumamos 9 para luego multiplicar todo por 5.
[4(5 x+6)+9] 5
Comparando con las opciones, escogemos como correcta a la d).
Reactivo 46: Proporciones
Una cubeta contiene una mezcla de pintura y agua. Si la mezcla ocupa \frac{4}{5} del volumen total de la cubeta y \frac{3}{4} del contenido es pintura ¿Cuántos litros de agua hay en la mezcla si la capacidad de la cubeta es de 40 litros?
- 32
- 24
- 16
- 8
Solución:
Para resolver el problema, entendamos los datos que nos ofrece el enunciado. Desde el inicio, se nos indica que la cubeta no está llena en su totalidad, solo se están ocupando \frac{4}{5} del volumen disponible. Si la cubeta es de 40 litros, se están ocupando:
V_{o c u}=\frac{(40 l) 4}{5}=32 l
Ahora, de esos 32 litros \frac{3}{4} partes son de pintura, es decir:
V_{\text {pin }}=(32 l) \cdot \frac{3}{4}=24 l
De esos 32 litros ocupados, 24 son de pintura por lo tanto, el volumen restante es de agua. El volumen ocupado puede expresarse como la suma del volumen de agua más el volumen de pintura.
V_{o c u}=V_{H_{2} O}+V_{p i n}
Despejamos entonces el volumen de agua.
V_{H_{2} O}=V_{\text {ocu }}-V_{\text {pin }} \rightarrow V_{H_{2} O}=32 l-24 l
V_{H_{2} O}=8 l
En la cubeta hay 8 litros de agua. En base a las opciones del problema, seleccionamos como correcta a la d).
Reactivo 47: Comparación de números reales
¿Cuál número es menor a 7/13?
- 6/9
- 6/10
- 6/11
- 6/12
Solución:
En este caso tenemos varias opciones: resolver las fracciones y comparar los números decimales, aplicar una propiedad de las fracciones o restar una fracción con otra. Esta vez aplicaremos una propiedad de las fracciones.
Dada una fracción, si el numerador es menor al denominador el cociente de ambos será menor que 1. Apoyados en eso, solo nos queda dividir cada una de las opciones por 7/13, si después de simplificar, el numerador resulta ser menor que el denominador y concluimos que 7/13 es mayor.
Fracción 6/9.
\frac{\frac{6}{9}}{\frac{7}{13}}=\frac{26}{21}
El numerador es mayor al denominador, por tanto 6/9 es mayor que 7/13.
Fracción 6/10.
\frac{\frac{6}{10}}{\frac{7}{13}}=\frac{39}{35}
El numerador es mayor al denominador, por tanto 6/10 es mayor que 7/13.
Fracción 6/11.
\frac{\frac{6}{11}}{\frac{7}{13}}=\frac{78}{77}
El numerador es mayor al denominador, por tanto 6/11 es mayor que 7/13.
Fracción 6/12.
\frac{\frac{6}{12}}{\frac{7}{13}}=\frac{13}{14}
El numerador es menor al denominador, por tanto 7/13 es mayor que 6/12.
Concluimos entonces que el número del inciso d) es menor que 7/13.
Reactivo 48: Problemas matemáticos
En una casa a la orilla del mar todos los días a las 18:00 horas, cuando comienza a subir la marea, ya hay 2 escalones de 20 cm cada uno sumergidos en el agua y cada hora la marea sube 10 cm ¿Cuántos escalones están sumergidos a las 0:00 horas?
- 3
- 4
- 5
- 6
Solución:
Ya que los escalones son de 20 cm y la marea incrementa en 10 cm cada hora, podemos decir entonces que al pasar una hora la marea se sumerge medio escalón (10 cm es la mitad de 20 cm). Desde las 18:00 horas hasta las 0:00 horas hay un total de 6 horas.
Con esto podemos hacer la siguiente relación:
Si en 1 hora se sumerge medio escalón, pasadas 6 horas se sumergen x escalones.
\text { 1hora } \rightarrow \frac{1}{2} \text { escalón }
6 \text { horas } \rightarrow x
x=\frac{6 h \cdot \frac{1}{2} e s c}{1 h}=3 \text { escalones }
Sumando los 2 escalones del comienzo, tenemos entonces un total de 5 escalones sumergidos a las 0:00 horas. Comparando con las opciones, escogemos como correcta a la c).
Materiales de estudio
Reactivo 49: Proporciones
Luis recorre el parque de su ciudad, en la primera hora recorrió 3/8 del viaje, durante la segunda hora 5/12 ¿Cuánto tendrá que recorrer la tercera para concluir el viaje?
- 8/4
- 15/36
- 5/24
- 8/96
Solución:
Sabemos que la suma total de los recorridos en las tres horas debe ser 1, relación que puede expresarse como:
V_{1 h}+V_{2 h}+V_{3 h}=1
Sabemos además que en la primera hora recorrió 3/8 del viaje total y en la segunda 5/12. Sustituimos y nos queda:
\frac{3}{8}+\frac{5}{12}+V_{3 h}=1
Para calcular la proporción que debe recorrer en la tercera hora, simplemente despejamos V_{3 h} de la ecuación.
\frac{3}{8}+\frac{5}{12}+V_{3 h}=1 \rightarrow V_{3 h}=1-\frac{3}{8}-\frac{5}{12}
Finalmente.
V_{3 h}=1-\frac{3}{8}-\frac{5}{12}=\frac{5}{24}
Luis debe recorrer 5/24 del viaje en la tercera hora para acabarlo. Comparando con las opciones, escogemos como correcta a la del inciso c).
Reactivo 50: Proporciones
Tres personas reciben una herencia. La primera recibe 2/5 del total y la segunda recibe 3/10 del total ¿Cuánto le corresponde a la tercera persona del total de la herencia?
- 5/15
- 7/15
- 2/10
- 3/10
Solución:
Imaginemos que la herencia es un pastel que debe partirse en 3 trozos. El pastel completo tiene una proporción de 1 a 1, es decir \frac{1}{1}=1 , mientras que las herencias para cada una de las tres personas es una proporción menor a uno y que juntas suman 1.
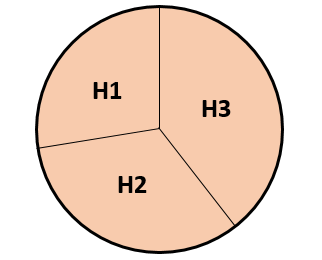
A partir de lo anterior, podemos establecer que:
H_{1}+H_{2}+H_{3}=1
Despejamos a \mathrm{H}_{3} , sustituimos y así calculamos cuánto le corresponde.
H_{3}=1-H_{1}-H_{2}
H_{3}=1-\frac{2}{5}-\frac{3}{10}=\frac{3}{10}
A la tercera persona le corresponden 3/10 de la herencia total.
Comparando con las opciones, la respuesta correcta es la del inciso d).
