¿Tienes dudas para resolver la guía del IPN 2023? En este tutorial vamos a desarrollar los 40 ejercicios de geometría analítica paso a paso para ayudarte a superar tu examen de ingreso a la universidad.

Por motivos didácticos hemos dividido la guía de geometría analítica en cuatro partes. De esta manera podrás establecer un horario de estudio, con pausas de recreación para permitir la oxigenación cerebral, muy importante para mejorar la memoria.
En esta ocasión vamos a resolver la primera parte de los reactivos del 1 al 10.
Te dejo un resumen de la convocatoria IPN.
- Carreras ofertadas en IPN: 70+.
- Porcentaje de Aceptación: 20%.
- Preguntas en el examen de Admisión: 140 preguntas.
- Nuevos temas: historia e inglés (reading comprehension).
- Tipo: selección múltiple.
Estructura del Examen IPN
La estructura del examen al IPN 2023 ha sido modificada. Ahora, el número de reactivos cambia según el área de conocimientos. Las carreras en el Instituto Politécnico Nacional se dividen en 3 áreas:
- Ingeniería y Ciencias Físico Matemáticas IyCFM
- Ciencias Sociales y Administrativas CSA
- Ciencias Médico Biológicas CMB
La siguiente tabla muestra la estructura de reactivos por materia para cada área.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
¿Qué tan difícil es el examen al IPN?
La verdad es que depende de tu preparación antes del examen. Por ello, tu compromiso con el aprendizaje debe ser constante, en especial para los temas más complejos como cálculo, probabilidad y estadística y geometría analítica.
Para esta convocatoria se incluyen 2 nuevas asignaturas, alterando la estructura de la prueba con respecto a años anteriores. En la guía de geometría analítica se incluyen reactivos que cubren los temas de la asignatura con diferentes niveles de complejidad.
Temario geometría analítica IPN 2023
Estos son los temas de geometría analítica que deberás estudiar para presentar el examen:
- Geometría analítica
- Conceptos básicos
- Plano cartesiano
- Línea recta
- Cónicas
- Circunferencia
- Parábola
- Elipse
- Hipérbola
- Coordenadas polares
- Plano polar
- Conceptos básicos
¿Cómo resolver la guía del IPN 2023?
Te aconsejo examinar la bibliografía recomendada en la guía antes de pasar con los reactivos. Un error común entre los aspirantes es estudiar los temas mientras resuelven la guía. De esta manera, no sigues un plan de estudio acorde a tus necesidades.
Los siguientes hacks te ayudarán a mejorar el desempeño, resolviendo la mayor cantidad de reactivos en el menor tiempo para obtener los aciertos que necesitas para ser admitido.
- Resuelve cada parte por tu cuenta antes de mirar las respuestas. Utiliza este material a modo de consulta.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
- Te advierto que la guía del IPN 2023 tiene algunos errores, aquí te señalamos cuáles son.
- Ayúdate con herramientas para geometría en línea como Geogebra. Así podrás comprobar el resultado e incluso salir de alguna duda.
Reactivo 1
Identificar los 3 puntos que son colineales en el plano cartesiano.
- A\left(1,\frac{3}{2}\right),B\left(3,-\frac{1}{2}\right)\text{ y }C\left(2,\frac{1}{2}\right)
- A\left(1,-\frac{3}{2}\right),B\left(3,-\frac{1}{2}\right)\text{ y }C\left(2,\frac{1}{2}\right)
- A\left(-1,\frac{3}{2}\right),B\left(3,-\frac{1}{2}\right)\text{ y }C\left(2,\frac{1}{2}\right)
- A\left(1,\frac{3}{2}\right),B\left(2,-\frac{1}{2}\right)\text{ y }C\left(2,\frac{1}{2}\right)
Solución:
De la geometría euclidiana sabemos que por dos puntos pasa una única recta, pero cuando tenemos 3 puntos debemos emplear otras técnicas para determinar si son colineales. Antes de indicar las alternativas que tenemos, vamos a examinar los incisos para descartar opciones.
Lo primero es que los incisos a, b y c tienen las mismas coordenadas para los puntos B y C . Por otra parte, en el inciso d los puntos B y C tienen la misma coordenada en x , esto significa que la recta que los une es vertical.
Ya que la coordenada del punto A en dicho inciso es 1, no es posible unir a los tres puntos con una misma recta. Descartamos al inciso d).
Ahora, la comprobación de colinealidad se puede hacer de forma gráfica, empleando la ecuación de la recta o mediante vectores. En este caso, es más práctico la opción de la línea recta. El procedimiento para comprobar será el siguiente:
- Encontramos la ecuación de la recta que pasa por los puntos B y C
- Sustituimos las coordenadas del punto A para cada inciso, aquel que satisfaga la ecuación es colineal con B y C
Ecuación de la recta.
m=\frac{{y}_{c}-{y}_{b}}{{x}_{c}-{x}_{b}}=\frac{\frac{1}{2}+\frac{1}{2}}{2-3}=-1
y-{y}_{o}=m\left(x-{x}_{o}\right)
Sustituimos al punto B\left(3,-\frac{1}{2}\right) .
y+\frac{1}{2}=-\left(x-3\right)\to y=-x+3-\frac{1}{2}
y=-x+\frac{5}{2}
Evaluamos el punto A del inciso a.
A\left(1,\frac{3}{2}\right)\to \frac{3}{2}=-1+\frac{5}{2}
\frac{3}{2}=\frac{3}{2}
Los puntos A\left(1,\frac{3}{2}\right),B\left(3,-\frac{1}{2}\right)\text{ y }C\left(2,\frac{1}{2}\right) son colineales.
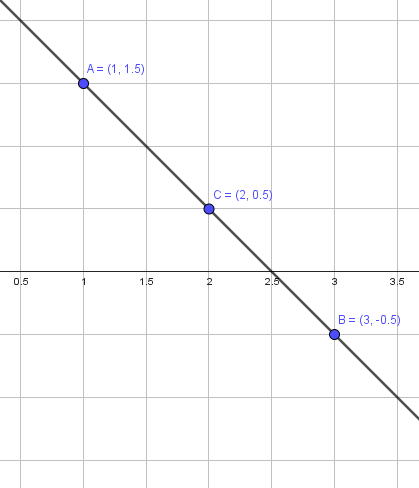
La respuesta correcta es el inciso a).
¿Vas a aplicar al IPN?, ¿Y no sabes cómo? Conoce todo sobre la siguiente convocatoria del IPN.
Reactivo 2
Identificar el cuadrante donde se localiza el punto medio del segmento que une los puntos P\left(\mathrm{5,6}\right)\text{ y }Q(-4,-7) .
- I
- II
- III
- IV
Solución:
Las coordenadas del punto medio que divide al segmento formado por dos puntos se calculan como:
M\left(P,Q\right)=\left(\frac{{P}_{x}+{Q}_{x}}{2},\frac{{P}_{y}+{Q}_{y}}{2}\right)
Sustituimos las coordenadas de los puntos.
M\left(P,Q\right)=\left(\frac{5-4}{2},\frac{6-7}{2}\right)=\left(\frac{1}{2},-\frac{1}{2}\right)
Debido a que la abscisa es positiva y la ordenada negativa, el punto se encuentra en el cuarto cuadrante (IV).
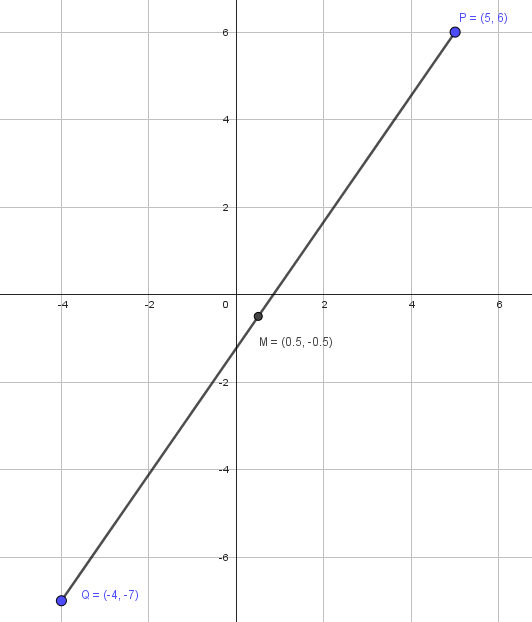
La respuesta correcta es el inciso d).
Reactivo 3
Calcular las coordenadas del punto medio del segmento con extremos A(-6,-5)\text{ y }B(3,-1) .
- \left(-\frac{3}{2},-3\right)
- \left(-\frac{3}{2},-2\right)
- \left(-\frac{4}{3},-3\right)
- \left(-\frac{4}{3},-2\right)
Solución:
El punto medio que divide a cualquier segmento, dados sus extremos, se calcula mediante la siguiente ecuación:
M\left(A,B\right)=\left(\frac{{A}_{x}+{B}_{x}}{2},\frac{{A}_{y}+{B}_{y}}{2}\right)
Sustituimos las coordenadas.
M\left(A,B\right)=\left(\frac{-6+3}{2},\frac{-5-1}{2}\right)=\left(-\frac{3}{2},-3\right)
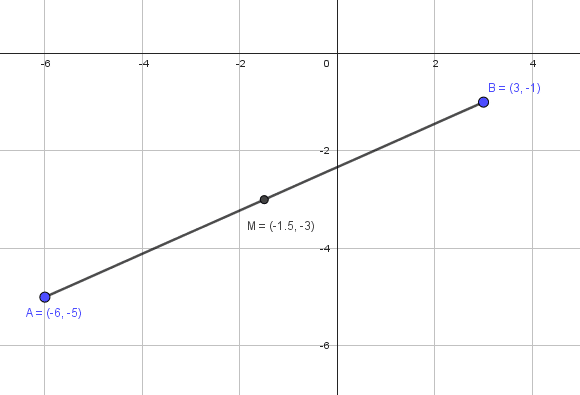
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 4
Relacionar el segmento con la distancia que le corresponde, en virtud de los puntos que se muestran en el sistema de coordenadas siguiente:
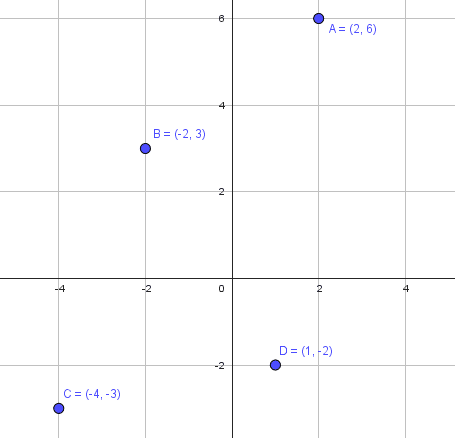

- 1C, 2B, 3A, 4D
- 1D, 2A, 3B, 4C
- 1C, 2A, 3B, 4D
- 1D, 2B, 3A, 4C
Solución:
Solo debemos calcular las distancias BC y AD , ya que esta es información suficiente para seleccionar alguno de los incisos. Las coordenadas de los puntos son:
A=\left(2, 6\right)
B=\left(-2, 3\right)
C=\left(-4, -3\right)
D=\left(1, -2\right)
Ecuación de distancia entre dos puntos:
d\left(A, B\right)=\sqrt{{\left({x}_{a}-{x}_{b}\right)}^{2}+{\left({y}_{a}-{y}_{b}\right)}^{2}}
Cálculo de la distancia BC .
\stackrel{-}{BC}=\sqrt{{\left(-2+4\right)}^{2}+{\left(3+3\right)}^{2}}=\sqrt{4+36}=\sqrt{40}=\sqrt{4\cdot 10}=2\sqrt{10}
Tenemos que: 1D.
Cálculo de la distancia AD .
\stackrel{-}{AD}=\sqrt{{\left(2-1\right)}^{2}+{\left(6+2\right)}^{2}}=\sqrt{1+64}=\sqrt{65}
Tenemos que: 2B.
El único inciso que inicia 1D, 2B es el d). La respuesta correcta es la opción d).
Reactivo 5
Calcular el área de un triángulo formado por los puntos A(-\mathrm{7,1}),B(-\mathrm{2,4})\text{ y }C(7,1) .
- 20
- 21
- 22
- 23
Solución:
Para resolver este problema es necesario conocer las fórmulas que permiten calcular el área de un triángulo dados sus vértices. Si no fuese el caso, el procedimiento a mano para llegar al resultado sería extenso y no aplicable en el examen de admisión.
Tenemos dos fórmulas para calcular el área: una emplea vectores y la otra un determinante, ambas son equivalentes. Vamos a emplear la fórmula con el determinante porque es la más directa de las dos.
{A}_{t}=\frac{1}{2}\mathrm{a}\mathrm{b}\mathrm{s}\left[\left|\begin{array}{ccc}{x}_{1}& {y}_{1}& 1\\ {x}_{2}& {y}_{2}& 1\\ {x}_{3}& {y}_{3}& 1\end{array}\right|\right]
Sustituimos los valores y desarrollamos el determinante.
\frac{1}{2}\mathrm{a}\mathrm{b}\mathrm{s}\left[\left|\begin{array}{ccc}-7& 1& 1\\ -2& 4& 1\\ 7& 1& 1\end{array}\right|\right]=\frac{1}{2}\mathrm{a}\mathrm{b}\mathrm{s}\left[\left|\begin{array}{cc}4& 1\\ 1& 1\end{array}\right|\left(-7\right)-\left|\begin{array}{cc}-2& 1\\ 7& 1\end{array}\right|\left(1\right)+\left|\begin{array}{cc}-2& 4\\ 7& 1\end{array}\right|\left(1\right)\right]
\frac{1}{2}\mathrm{a}\mathrm{b}\mathrm{s}\left[\left(4-1\right)\left(-7\right)-\left(-2-7\right)+\left(-2-28\right)\right]=\frac{1}{2}\left|-21+9-30\right|
{A}_{t}=\frac{1}{2}\left|-42\right|=21 {\mathrm{u}}^{2}
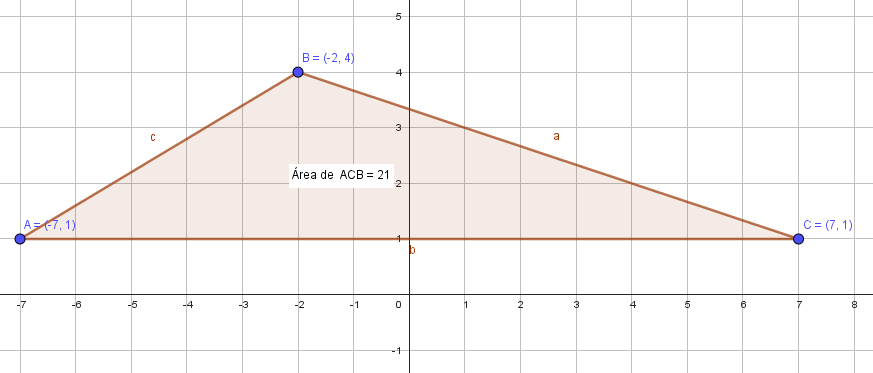
Concluimos indicando como respuesta correcta al inciso b).
Reactivo 6
Cuánto vale “a”, tal que la distancia entre los puntos A(a,-3) y el punto B(-a,-2) sea de 7.
- \pm 2\sqrt{3}
- \pm \sqrt{6}
- \pm 3\sqrt{2}
- \pm \sqrt{3}
Solución:
Este problema se puede resolver mediante dos enfoques:
- Calcular el valor de a planteando la ecuación de distancia entre dos puntos
- Sustituyendo los valores de a dados por los enunciados en la ecuación de distancia, e ir descartando hasta encontrar el valor que la satisfaga
En este caso particular, el camino más corto es el primero, debido a que solo tenemos que aplicar un despeje sobre el parámetro a .
Ecuación de distancia entre los puntos A y B .
d\left(A,B\right)=7\to \sqrt{{\left(a+a\right)}^{2}+{\left(-2+3\right)}^{2}}=7
\sqrt{4{a}^{2}+1}=7
Despejamos el parámetro a .
4{a}^{2}+1=49\to 4{a}^{2}=48\to {a}^{2}=12
Aplicamos raíz en ambos lados. No olvides que se coloca \pm en el miembro sobre el que permanece la raíz cuadrada.
\therefore a=\pm \sqrt{12}=\pm \sqrt{3\cdot 4}=\pm 2\sqrt{3}
a=\pm 2\sqrt{3}
Concluimos el problema indicando como respuesta correcta al inciso a).
Reactivo 7
Determinar el punto de intersección de las siguientes rectas:
\begin{array}{c}x+\frac{y}{3}=\frac{2}{3}\\ \frac{x}{3}-y=-\frac{2}{3}\end{array}
- \left(\frac{1}{5},\frac{3}{5}\right)
- \left(\frac{2}{5},\frac{3}{5}\right)
- \left(\frac{2}{5},\frac{4}{5}\right)
- \left(\frac{3}{5},\frac{4}{5}\right)
Solución:
Calcular la intersección entre dos rectas, significa resolver el sistema de ecuaciones que estas representan. Antes de continuar, multiplicamos ambas expresiones por 3 para eliminar las fracciones.
\begin{array}{c}x+\frac{y}{3}=\frac{2}{3}\\ \frac{x}{3}-y=-\frac{2}{3}\end{array}\to \begin{array}{c}3x+y=2\\ x-3y=-2\end{array}
\left\{\begin{array}{c}3x+y=2\\ x-3y=-2\end{array}\right.
Para resolver el SEL podemos aplicar cualquier método: sustitución, igualación, reducción, matrices o por determinantes. En este caso, es más práctico aplicar reducción. Multiplicamos a la primera ecuación por 3.
\left\{\begin{array}{c}3x+y=2\\ x-3y=-2\end{array}\right.\to \left\{\begin{array}{c}9x+3y=6\\ x-3y=-2\end{array}\right.
Sumamos las ecuaciones.
\begin{array}{c}9x+3y=6\\ x-3y=-2\end{array}
10x=4\to x=\frac{2}{5}
Sustituimos este resultado en la primera ecuación y despejamos a y .
3\left(\frac{2}{5}\right)+y=2\to y=2-\frac{6}{5}=\frac{4}{5}
Finalmente, el punto de intersección entre las rectas es: PI\left(\frac{2}{5},\frac{4}{5}\right) .
Seleccionamos como respuesta correcta al inciso c).
Reactivo 8
Identificar la ecuación de la recta perpendicular a 7y=2x+11 que pasa por (0, -5) .
- y=-\frac{7}{2}x-10
- 2y=-7x-5
- 2y=-7x-10
- y=-7x-5
Solución:
En este problema, debemos utilizar la condición de perpendicularidad entre rectas:
{m}_{1}{m}_{2}=-1
Es decir, que el producto de las pendientes sea igual a -1. Obtenemos la pendiente de la recta dada.
7y=2x+11\to y=\frac{2}{7}x+\frac{11}{7}
{m}_{1}=\frac{2}{7}
Sustituimos en la condición.
{m}_{2}=-\frac{1}{{m}_{1}}=-\frac{1}{\frac{2}{7}}=-\frac{7}{2}
\therefore {m}_{2}=-\frac{7}{2}
Sustituimos a la pendiente y el punto (0, -5) en la ecuación punto pendiente de la recta.
y-{y}_{o}={m}_{2}\left(x-{x}_{o}\right)\to y+5=-\frac{7}{2}\left(x+0\right)
y+5=-\frac{7}{2}x\to y=-\frac{7}{2}x-5
Multiplicamos ambos lados por 2.
2y=-7x-10
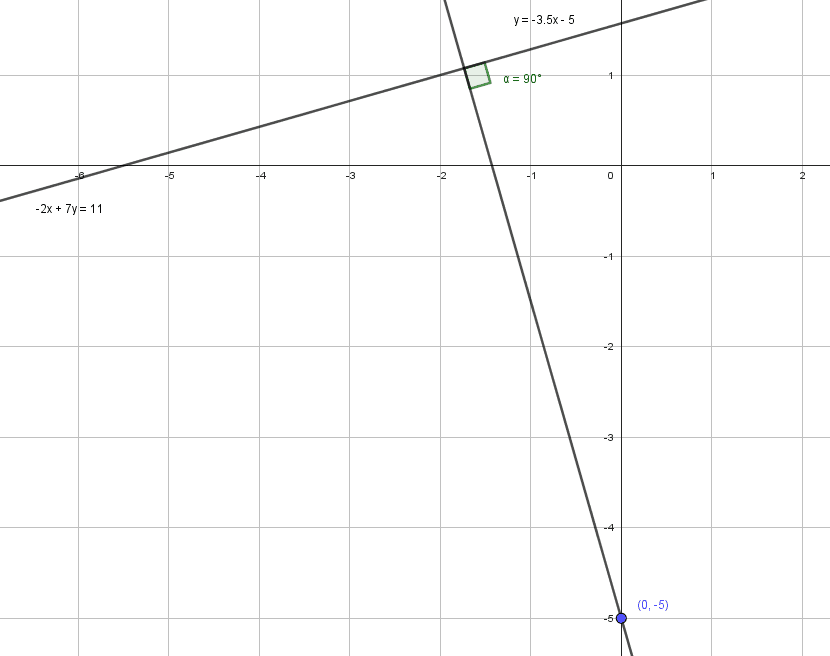
La respuesta correcta es el inciso c).
Reactivo 9
Determinar la ecuación de la recta dados los puntos A\left(\mathrm{1,2}\right) y B\left(\mathrm{3,3}\right)
- x+2y=3
- x+y=3
- x+2y=-3
- -x+2y=3
Solución:
Para encontrar la ecuación de cualquier recta, necesitamos su pendiente m y un punto. La pendiente la calculamos mediante los puntos suministrados por el enunciado.
Ecuación punto – pendiente de la recta.
y-{y}_{o}=m\left(x-{x}_{o}\right)
Calculamos la pendiente.
m=\frac{{y}_{b}-{y}_{a}}{{x}_{b}-{x}_{a}}=\frac{3-2}{3-1}=\frac{1}{2}
Sustituimos el punto A .
y-2=\frac{1}{2}\left(x-1\right)\to y-2=\frac{x}{2}-\frac{1}{2}
\therefore y=\frac{x}{2}+\frac{3}{2}
Multiplicamos todo por 2.
2y=x+3\to -x+2y=3
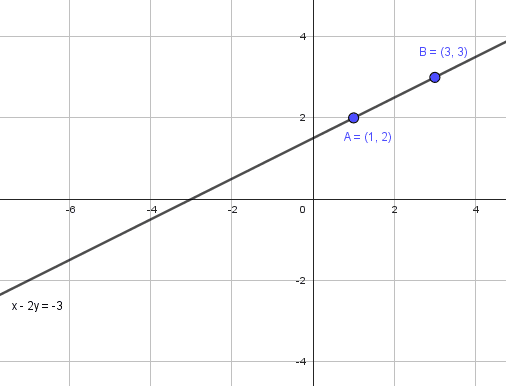
Concluimos indicando como respuesta correcta la opción d).
Reactivo 10
Identificar la ecuación de la recta dados un punto y su pendiente.
- y=mx+b
- y=mx-b
- \left(y-{y}_{0}\right)=m\left(x-{x}_{0}\right)
- \left(y-{y}_{0}\right)=\left(\frac{{y}_{1}-{y}_{0}}{{x}_{1}-{x}_{0}}\right)\left(x-{x}_{0}\right)
Solución:
La ecuación punto pendiente de la recta es:
y-{y}_{o}=m\left(x-{x}_{o}\right)
La respuesta correcta es el inciso d).


