Vamos con la solución de la segunda y última parte de los reactivos de matemáticas área 3, del 53 al 64, en la guía de las Ciencias Sociales como preparación al examen de ingreso a la UNAM.

El siguiente resumen indica los puntos clave el examen UNAM:
- Desarrollo: UNAM
- Área 3: Ciencias Sociales
- Materia: Matemáticas
- Reactivos: 120
- Tipo: Opción múltiple
- Duración: 3 horas
- Modalidades: Presencial
¡Felicidades por llegar hasta aquí aspirante! Matemáticas muchas veces se entiende como una asignatura de fórmulas y despejes, pero en ella encontramos los modelos para comprender el mundo que nos rodea.
Guía matemáticas UNAM área 3 resuelta
Vamos con los últimos 12 ejercicios de matemáticas de la guía del Área 3 de las Ciencias Sociales de la UNAM. Recuerda tomar descansos entre grupos de ejercicios, esto también forma parte del proceso de aprendizaje.
Te invito a continuar aprendiendo con el resto de guías resueltas de la UNAM, maratones de reactivos y clases.
Reactivo 53
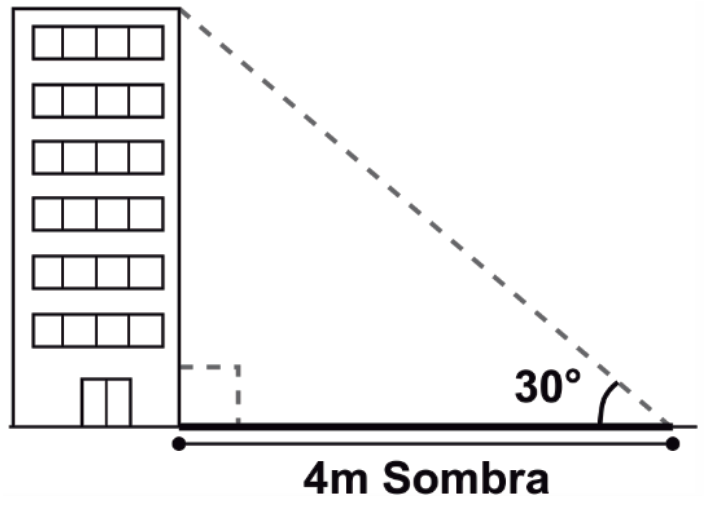
Un edificio hace una sombra de 4 metros con un ángulo de inclinación sobre el piso de 30°. ¿Cuál es la altura del edificio?
- \frac{4\sqrt{3}}{3} \mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
- 2 \mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
- 8 \mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
- \frac{2\sqrt{3}}{3} \mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
Solución:
Debido a que la sombra, la altura y la línea punteada forman un triángulo rectángulo, podemos aplicar relaciones trigonométricas para calcular la altura del edificio. Respecto del ángulo de 30°, la altura es el cateto opuesto y la sombra el cateto adyacente.
Empleamos la tangente de 30°.
\mathrm{tan}30°=\frac{CO}{CA}\to \mathrm{tan}30°=\frac{h}{4}
Despejando nos queda:
h=4\mathrm{tan}30°
La tangente de 30° es igual a \frac{\sqrt{3}}{3} . Finalmente:
h=4\frac{\sqrt{3}}{3}\mathrm{ }\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
La respuesta correcta es el inciso A.
Reactivo 54
Determina el valor del lado p del siguiente triángulo. Considera:
\begin{array}{c}\mathrm{sin}\left(40°\right)=0.64\\ \mathrm{sin}\left(100°\right)=0.98\\ \begin{array}{c}\mathrm{cos}\left(40°\right)=0.76\\ \mathrm{cos}\left(100°\right)=0.17\end{array}\end{array}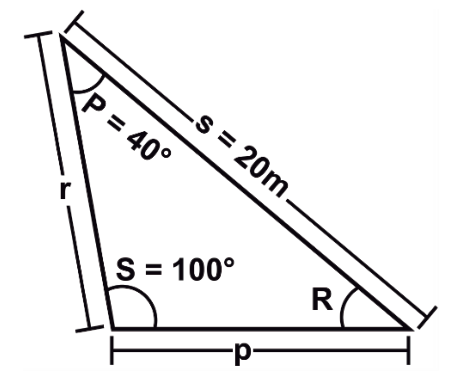
- 16.10 m
- 13.06 m
- 18.34 m
- 30.64 m
Solución:
Analizando el triángulo, determinamos que el lado p se puede calcular aplicando la ley de los senos, debido a que conocemos el ángulo opuesto a p y conocemos al lado s con su respectivo ángulo opuesto S=100° .
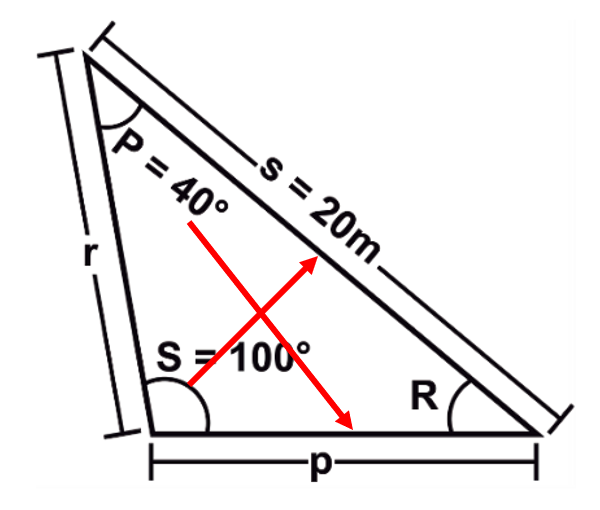
\frac{p}{\mathrm{sin}40°}=\frac{20}{\mathrm{sin}100}
Despejamos a p y calculamos.
p=\frac{\mathrm{sin}40}{\mathrm{sin}100}\left(20\right)=\frac{0.64}{0.98}\left(20\right)=13.06 \mathrm{m}
El lado p mide 13.06 metros.
La respuesta correcta es el inciso B.
Reactivo 55
Determina el dominio de la siguiente función.
y=\mathrm{log}\left(x-2\right)
- \left(2, \infty \right)
- \left[2,\infty \right)
- \left(-\infty , 2\right)
- \left(-\infty , 2\right]
Solución:
Para calcular el dominio de cualquier función real, primero debemos identificar qué funciones elementales la componen y luego determinamos sus restricciones. En este caso, la función es logarítmica base 10, cuya única restricción es que el argumento sea mayor que 0.
x-2>0
Por lo tanto:
x>2
Expresado en notación de conjunto:
\mathrm{D}\mathrm{o}\mathrm{m}\left(y\right)=x\in \left(2, \infty \right)
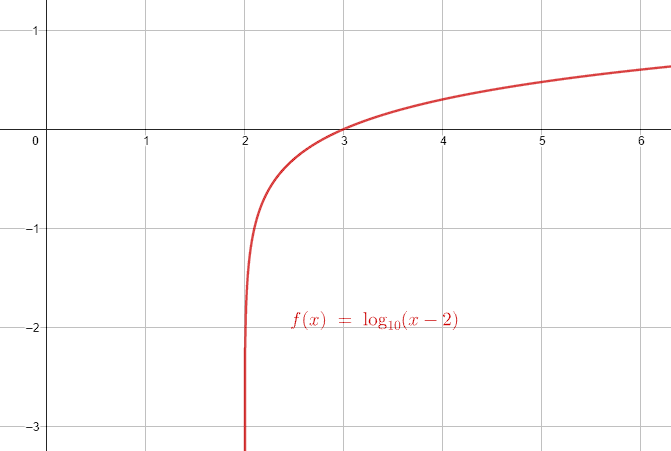
La respuesta correcta es el inciso A.
Reactivo 56
¿Cuál es la distancia entre los puntos P\left(2, 5\right) y Q\left(4, -1\right) ?
- 2\sqrt{3}
- 2\sqrt{5}
- 2\sqrt{2}
- 2\sqrt{10}
Solución:
Para calcular la distancia entre dos puntos en el plano, utilizamos la siguiente ecuación:
d\left(P,Q\right)=\sqrt{{\left({P}_{x}-{Q}_{x}\right)}^{2}+{\left({P}_{y}-{Q}_{y}\right)}^{2}}
Sustituimos las coordenadas de los puntos.
d\left(P,Q\right)=\sqrt{{\left(2-4\right)}^{2}+{\left(5+1\right)}^{2}}=\sqrt{4+36}=\sqrt{40}
Finalmente:
d\left(P,Q\right)=2\sqrt{10}\approx 6.3245
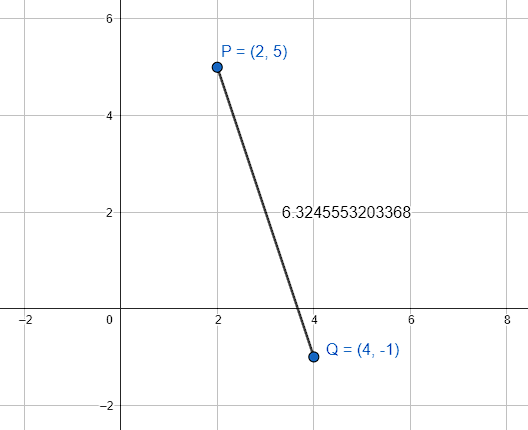
La respuesta correcta es el inciso D.
Reactivo 57
Calcula la pendiente de la recta cuya función es -4x+2y+3=0 .
- -2
- -\frac{1}{2}
- \frac{3}{2}
- 2
Solución:
A partir de la forma general de la recta Ax+By+C=0 , la pendiente se puede calcular como:
m=-\frac{A}{B}
Evaluamos:
m=-\frac{-4}{2}=2
La pendiente de la recta es igual a 2 unidades.
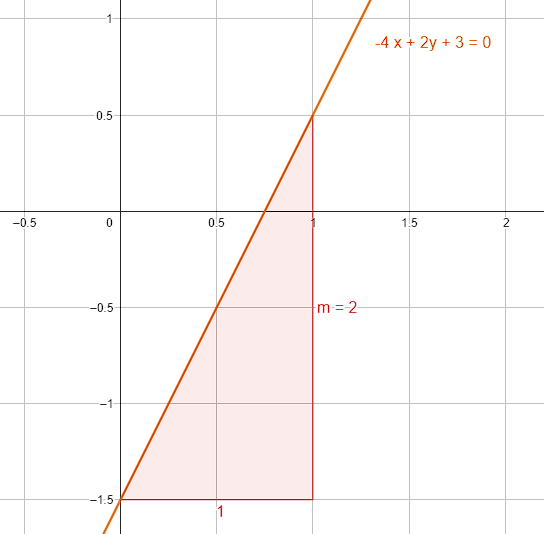
Concluimos indicando como respuesta correcta al inciso D.
Reactivo 58
¿Qué ecuación describe la siguiente gráfica?
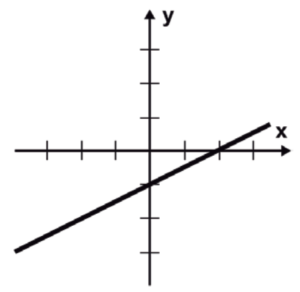
- y=x-\frac{1}{2}
- y=\frac{3}{2}x-\frac{1}{2}
- y=-\frac{1}{2}x-1
- y=\frac{x}{2}-1
Solución:
El problema se puede resolver mediante dos enfoques: obteniendo los puntos de corte con los ejes de las rectas en los incisos o construyendo la ecuación de la recta en el gráfico, para luego compararlo con los incisos.
Debido a que la primera opción puede llevar mucho tiempo, calcularemos la ecuación de la recta. Iniciamos identificando que los cortes con los ejes son: \left(\mathrm{2,0}\right) y \left(0, -1\right) . Empleamos la ecuación simétrica de la recta:
\frac{x}{a}+\frac{y}{b}=1
Donde a y b son los cortes con el eje x y y respectivamente. Sustituimos:
\frac{x}{2}+\frac{y}{-1}=1\to \frac{x}{2}-y=1
Finalmente:
y=\frac{x}{2}-1
Comparando con los incisos, concluimos que la respuesta correcta es la opción D.
Reactivo 59
¿Cuál es la ecuación de la circunferencia que tiene centro en el origen y radio igual a 4?
- {x}^{2}+{y}^{2}+16=0
- {x}^{2}+{y}^{2}-16=0
- {x}^{2}+{y}^{2}-4=0
- {x}^{2}+{y}^{2}+4=0
Solución:
Cuando una circunferencia se encuentra centrada en el origen, no hay término lineal en la forma general de la circunferencia para ninguna de las variables. Con lo anterior no podemos descartar ningún inciso, porque todas se encuentran centradas en el origen.
Por otra parte, el cuadrado del radio viene representado por el término independiente de la ecuación y este es negativo en la forma general. El cuadrado de 4 es 16 y la única circunferencia con -16 en el primer miembro es la del inciso B.
Reactivo 60
Indica el centro y el radio de la circunferencia {x}^{2}+{y}^{2}=20 .
- C\left(\mathrm{0,0}\right);R=20
- C\left(1,1\right);R=20
- C\left(-1,-1\right);R=\sqrt{20}
- C\left(\mathrm{0,0}\right);R=\sqrt{20}
Solución:
Examinando la ecuación suministrada, sabemos que la circunferencia se encuentra centrada en el origen, descartamos a los incisos B y C. Por otra parte, el radio es igual a la raíz cuadrada del término independiente:
r=\sqrt{20}
Con esta información podemos concluir que la respuesta correcta es el inciso D.
Reactivo 61
Un objeto es lanzado describiendo la parábola {\left(x-4\right)}^{2}=12\left(y-3\right) , ¿cuáles son las coordenadas del vértice y el foco?
- V\left(-4,-3\right);F\left(-4,-6\right)
- V\left(3, 4\right);F\left(6, 4\right)
- V\left(4, 3\right);F\left(4, 6\right)
- V\left(-3,-4\right);F\left(-6,-4\right)
Solución:
Analizando la ecuación, esta describe a una parábola vertical, que abre hacia arriba y que tiene vértice en el punto \left(4, 3\right) . Debido a que solo un inciso tiene como vértice al punto \left(4, 3\right) , podemos concluir que la respuesta correcta es la opción C.
Reactivo 62
¿Cuál es el centro de una elipse cuya ecuación es \frac{{\left(x-2\right)}^{2}}{144}+\frac{{\left(y-1\right)}^{2}}{64}=1 ?
- \left(-2, -1\right)
- \left(2, 1\right)
- \left(1, 2\right)
- \left(-1, -2\right)
Solución:
El centro de la elipse se puede extraer directamente de la ecuación:
\frac{{\left(x-h\right)}^{2}}{{a}^{2}}+\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1
Las coordenadas del centro son \left(h, k\right) . Por lo tanto:
C\left(h, k\right)=\left(2, 1\right)
La respuesta correcta es el inciso B.
Reactivo 63
La hipérbola es el lugar geométrico de los puntos del plano, tales que la:
- suma de sus distancias a dos puntos fijos es un valor variable.
- diferencia de sus distancias a dos puntos fijos es un valor constante.
- suma de sus distancias a dos puntos fijos es un valor constante.
- diferencia de sus distancias a dos puntos fijos es un valor variable.
Solución:
La definición analítica de una hipérbola, es el punto cuyo valor absoluto de la diferencia de las distancias respecto a los focos, es igual a una constante y menor que la distancia entre los focos.
\left|\left|{F}_{1}P\right|-\left|{F}_{2}P\right|\right|=2a
\left|{F}_{1}{F}_{2}\right|<2a
Ahora, dichos focos son puntos fijos, por tanto, teniendo en cuenta lo enunciado y examinando los incisos, concluimos que la respuesta correcta se encuentra en el B.
Diferencia de sus distancias a dos puntos fijos es un valor constante.
Reactivo 64
¿Qué tipo de cónica representa la ecuación {y}^{2}+4x+2y+16=0 ?
- Parábola con vértice en el origen
- Elipse con centro fuera del origen
- Elipse con centro en el origen
- Parábola con vértice fuera del origen
Solución:
Al inspeccionar la ecuación, es fácil darse cuenta que se trata de una parábola, con eje focal horizontal y vértice fuera del origen, porque está el término lineal de y .
Podemos comprobar nuestra suposición mediante el discriminante para la ecuación general de segundo grado.
Ecuación general de segundo grado:
A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0
Discriminante:
{B}^{2}-4AC=0
Extrayendo los valores de la ecuación del enunciado:
B=0, A=0, C=1\to 0-4\left(0\right)\left(1\right)=0
Comparando con los incisos, la respuesta correcta es el D.


