Guía UNAM Matemáticas: Área 2 Cs Biológicas Químicas y Salud P.2

¡Continuamos aspirante! Vamos con la solución de la segunda y última parte de los reactivos de matemáticas área 2, del 58 al 69, en la guía de Ciencias Biológicas, Químicas y de la Salud correspondiente al examen de ingreso a la Universidad Nacional Autónoma de México.

El siguiente resumen contiene los puntos clave de la prueba de ingreso UNAM:

• Desarrollo: UNAM
• Área 2: Ciencias Biológicas, Químicas y de la Salud
• Materia: Matemáticas
• Reactivos: 120
• Tipo: Opción múltiple
• Duración: 3 horas
• Modalidades: Presencial

Las matemáticas representan un pilar importante en el desarrollo de cualquier carrera universitaria. Date el tiempo de comprender cada tema, lo necesitarás incluso estudiando la carrera.

Guía matemáticas UNAM área 2 resuelta

Continuamos resolviendo la segunda parte de reactivos de matemáticas para el área 2 de Ciencias Biológicas, Químicas y de la Salud como preparación al examen de ingreso a la Universidad Nacional Autónoma de México.

Reactivo 58

La distancia del punto $\left(-1, 1\right)$ a la recta dada por la ecuación $-3x+4y-8=0$ es:

1. 2 unidades.
2. 2 unidades.
3. 25 unidades.
4. 8 unidades.

Solución:

Para calcular la distancia entre un punto y una recta, se utiliza la siguiente ecuación:

$d\left(P,l\right)=\frac{\left|A\cdot {p}_{x}+B\cdot {p}_{y}+C\right|}{\sqrt{{A}^{2}+{B}^{2}}}$

Donde $A, B$ y $C$ son los coeficientes de la recta y $\left({p}_{x},{p}_{y}\right)$ son las coordenadas del punto. Para efectos del problema:

$A=-3, B=4, C=-8$

$\left({p}_{x},{p}_{y}\right)=\left(-\mathrm{1,1}\right)$

Sustituimos.

$d\left(P,l\right)=\frac{\left|-3\cdot -1+4\cdot 1-8\right|}{\sqrt{{\left(-3\right)}^{2}+{4}^{2}}}=\frac{\left|3+4-8\right|}{\sqrt{9+16}}=\frac{\left|-1\right|}{\sqrt{25}}$

$d\left(P,l\right)=\frac{1}{5}=0.2 \mathrm{u}\mathrm{n}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{d}\mathrm{e}\mathrm{s}$

La distancia entre la recta y el punto es igual a 0.2 unidades.

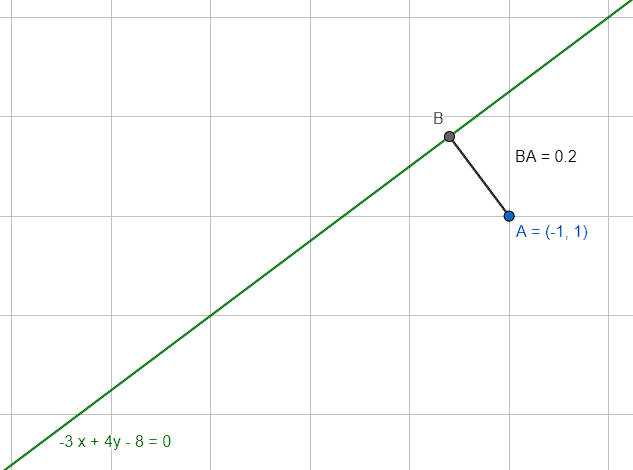
Concluimos que la respuesta correcta es el inciso A.

Reactivo 59

Indica las coordenadas del centro de la circunferencia cuya ecuación general es $3{x}^{2}+3{y}^{2}+12x+30y+6=0$.

1. $C\left(-4, -10\right)$
2. $C\left(-2, -5\right)$
3. $C\left(4, 10\right)$
4. $C\left(2, 5\right)$

Solución:

Estos problemas son bastante comunes y se pueden resolver de dos formas: completando cuadrados respecto a las variables de la circunferencia o, utilizando la fórmula del centro en función de los coeficientes de la circunferencia.

${x}^{2}+{y}^{2}+Dx+Ey+F=0$

En el momento del examen, lo ideal es utilizar el método más rápido. En este caso, el método más rápido es utilizar la ecuación. Necesitas memorizar, pero acortará el tiempo de solución de los problemas.

$C\left(-\frac{D}{2}, -\frac{E}{2}\right)$

Dividimos entre 3 a toda la ecuación de la circunferencia.

$3{x}^{2}+3{y}^{2}+12x+30y+6=0\to {x}^{2}+{y}^{2}+4x+10y+2=0$

Nos queda:

$D=4, E=10$

Sustituimos:

$C\left(-\frac{4}{2}, -\frac{10}{2}\right)=C\left(-2,-5\right)$

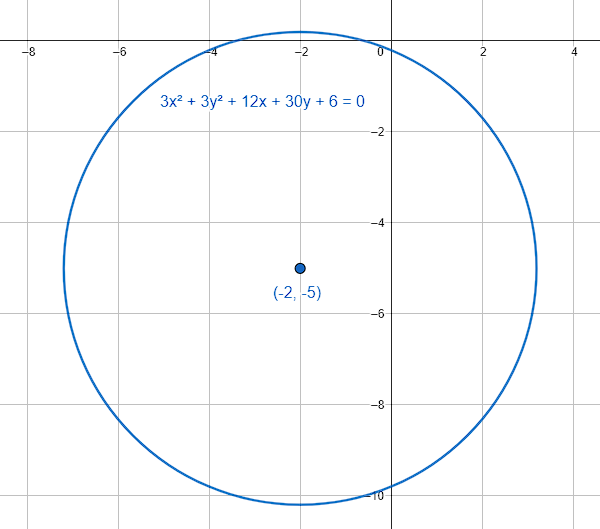
Concluimos que la respuesta correcta es el inciso B.

Reactivo 60

La ecuación de la parábola cuyo eje focal es el eje y, con el parámetro $p=-5$ y vértice en el origen es:

1. ${x}^{2}-20x=0$
2. ${y}^{2}-20x=0$
3. ${y}^{2}+20x=0$
4. ${x}^{2}+20y=0$

Solución:

El enunciado nos dice que la parábola es vertical. La ecuación ordinaria de una parábola vertical es:

$4p\left(y-k\right)={\left(x-h\right)}^{2}$

El vértice de la parábola es $\left(h, k\right)=\left(0, 0\right)$ y $p=-5$. El signo del parámetro $p$ indica que la parábola abre hacia abajo. Sustituimos:

${\left(x-0\right)}^{2}=4\left(-5\right)\left(y-0\right)\to {x}^{2}=-20y$

Finalmente:

${x}^{2}+20y=0$

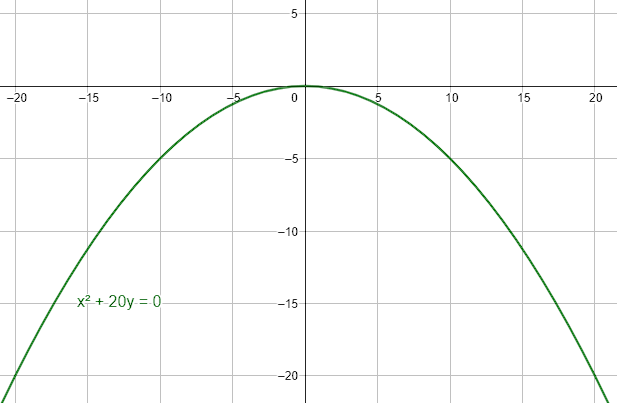
La respuesta correcta es el inciso D.

Reactivo 61

Lugar geométrico en el plano en el que la suma de las distancias de cualquiera de los puntos a dos puntos fijos llamados focos es una cantidad constante.

1. Elipse.
2. Circunferencia.
3. Hipérbola.
4. Parábola.

Solución:

Para responder esta pregunta, debemos conocer previamente la definición de los lugares geométricos de las cónicas, porque la demostración de los enunciados es extensa y compleja. Analizando el enunciado, concluimos que hace referencia a la elipse.

Elipse.

Es el lugar geométrico de un punto que se mueve en un plano de tal manera que la suma de su distancia a dos puntos fijos es siempre igual a una constante, mayor que la distancia entre los dos puntos.

$\left|FP\right|+\left|{F}^{\text{'}}P\right|=2a$

La respuesta correcta es el inciso A.

Reactivo 62

La ecuación de la hipérbola centrada en el origen, con lado recto 10 y vértice $V\left(0, -9\right)$ es:

1. $9{y}^{2}-5{x}^{2}=405$
2. $5{y}^{2}-9{x}^{2}=405$
3. $9{y}^{2}-10{x}^{2}=90$
4. $10{y}^{2}-9{x}^{2}=90$

Solución:

Iniciamos mencionando que el lado recto de la hipérbola es una cuerda focal perpendicular al eje focal y que tiene como valor:

$LR=\frac{2{b}^{2}}{{a}^{2}}$

Por otra parte, las coordenadas del vértice de la hipérbola nos dan información acerca de hacia dónde abre. Debido a que está centrada en el origen, la ordenada del vértice nos dice que es una hipérbola vertical.

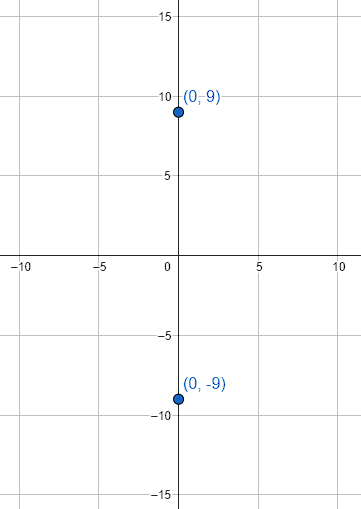
Por otra parte, sabemos que el vértice de una hipérbola es $V\left(0,\pm a\right)$, por lo tanto:

$a=9$

Con el valor de $a$ y del lado recto, despejamos el valor de $b$.

$LR=\frac{2{b}^{2}}{a}\to b=\pm \sqrt{\frac{aLR}{2}}$

Sustituimos.

$b=\pm \sqrt{\frac{\left(9\right)\left(10\right)}{2}}=\pm \sqrt{\frac{90}{2}}=\pm \sqrt{45}$

Finalmente, la ecuación de una hipérbola vertical centrada en el origen es:

$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1$

Sustituimos el valor de $a$ y $b$.

$\frac{{y}^{2}}{{\left(9\right)}^{2}}-\frac{{x}^{2}}{{\left(\sqrt{45}\right)}^{2}}=1\to \frac{{y}^{2}}{81}-\frac{{x}^{2}}{45}=1$

Simplificamos.

$45{y}^{2}-81{x}^{2}=3645$

Dividimos todo entre 9.

$5{y}^{2}-9{x}^{2}=405$

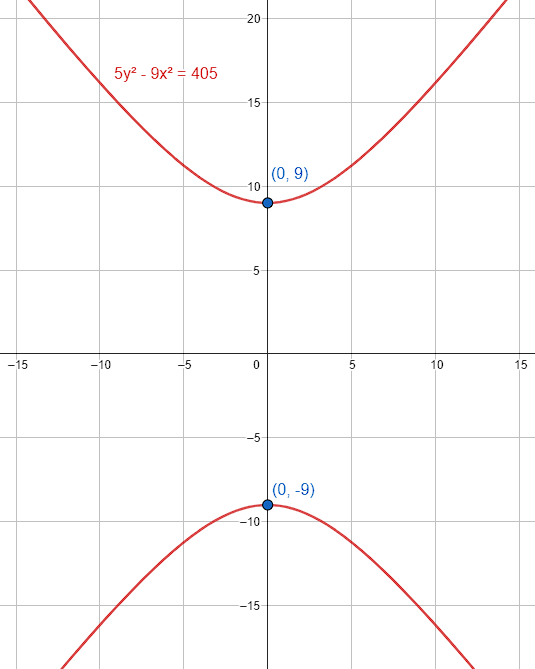
Indicamos como respuesta correcta al inciso B.

Reactivo 63

Selecciona el criterio utilizado para definir que la ecuación de segundo grado $A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0$ representa una elipse.

1. ${C}^{2}-4AB<0$
2. ${B}^{2}-4AC>0$
3. ${C}^{2}-4AB>0$
4. ${B}^{2}-4AC<0$

Solución:

Para determinar el tipo de cónica que representa la ecuación general de segundo grado, determinamos el signo del determinante de la cónica.

${B}^{2}-4AC$

En el caso específico de la elipse, el determinante debe ser menor que cero.

${B}^{2}-4AC<0$

La respuesta correcta es el inciso D.

Reactivo 64

Calcula el límite $\underset{x\to 0}{\mathrm{lim}}\frac{\sqrt{2+x}-\sqrt{2}}{x}$.

1. $\frac{\sqrt{2}}{2}$
2. $\frac{1}{\sqrt{2}}$
3. $\frac{1}{2}$
4. $\frac{\sqrt{2}}{4}$

Solución:

Iniciamos evaluando el límite para identificar el tipo de indeterminación.

$\underset{x\to 0}{\mathrm{lim}}\frac{\sqrt{2+x}-\sqrt{2}}{x}=\frac{\sqrt{2+0}-\sqrt{2}}{0}=\frac{\sqrt{2}-\sqrt{2}}{0}=\frac{0}{0}$

Indeterminación cero sobre cero. Multiplicamos y dividimos por el conjugado del numerador.

$\underset{x\to 0}{\mathrm{lim}}\frac{\sqrt{2+x}-\sqrt{2}}{x}\cdot \frac{\sqrt{2+x}+\sqrt{2}}{\sqrt{2+x}+\sqrt{2}}=\underset{x\to 0}{\mathrm{lim}}\frac{2+x-2}{x\left(\sqrt{2+x}+\sqrt{2}\right)}$

$\underset{x\to 0}{\mathrm{lim}}\frac{1}{\sqrt{2+x}+\sqrt{2}}$

Evaluamos nuevamente el límite.

$\underset{x\to 0}{\mathrm{lim}}\frac{1}{\sqrt{2+x}+\sqrt{2}}=\frac{1}{\sqrt{2+0}+\sqrt{2}}=\frac{1}{2\sqrt{2}}$

Finalmente:

$\underset{x\to 0}{\mathrm{lim}}\frac{\sqrt{2+x}-\sqrt{2}}{x}=\frac{\sqrt{2}}{4}$

Concluimos indicando como respuesta correcta al inciso D.

Reactivo 65

La derivada de la expresión $y=2{x}^{\frac{1}{2}}+6{x}^{\frac{1}{3}}$ es:

1. ${y}^{\text{'}}=2{x}^{\frac{1}{2}}+6{x}^{\frac{1}{3}}$
2. ${y}^{\text{'}}={x}^{\frac{1}{2}}+2{x}^{\frac{1}{3}}$
3. ${y}^{\text{'}}=-\frac{1}{{x}^{\frac{1}{2}}}-\frac{2}{{x}^{\frac{2}{3}}}$
4. ${y}^{\text{'}}=\frac{1}{{x}^{\frac{1}{2}}}+\frac{2}{{x}^{\frac{2}{3}}}$

Solución:

Iniciamos aplicando la propiedad de la derivada de una suma.

${y}^{\text{'}}={\left(2{x}^{\frac{1}{2}}+6{x}^{\frac{1}{3}}\right)}^{\text{'}}={\left(2{x}^{\frac{1}{2}}\right)}^{\text{'}}+{\left(6{x}^{\frac{1}{3}}\right)}^{\text{'}}=2{\left({x}^{\frac{1}{2}}\right)}^{\text{'}}+6{\left({x}^{\frac{1}{3}}\right)}^{\text{'}}$

Derivamos ambos términos aplicando la fórmula de la derivada de una potencia.

${y}^{\text{'}}=2{\left({x}^{\frac{1}{2}}\right)}^{\text{'}}+6{\left({x}^{\frac{1}{3}}\right)}^{\text{'}}=2\cdot \frac{1}{2}\left({x}^{\frac{1}{2}-1}\right)+6\cdot \frac{1}{3}\left({x}^{\frac{1}{3}-1}\right)$

${y}^{\text{'}}={x}^{-\frac{1}{2}}+2{x}^{-\frac{2}{3}}$

Finalmente:

${y}^{\text{'}}=\frac{1}{{x}^{\frac{1}{2}}}+\frac{2}{{x}^{\frac{2}{3}}}$

Comparando con los incisos, concluimos que la respuesta correcta es el D.

Reactivo 66

La derivada de $f\left(x\right)=\mathrm{ln}\sqrt{{x}^{2}+1}$ con respecto a $x$ es:

1. ${f}^{\text{'}}\left(x\right)=\frac{x}{2\sqrt{{x}^{2}+1}}$
2. ${f}^{\text{'}}\left(x\right)=\frac{x}{2\left({x}^{2}+1\right)}$
3. ${f}^{\text{'}}\left(x\right)=\frac{x}{x\sqrt{{x}^{2}+1}}$
4. ${f}^{\text{'}}\left(x\right)=\frac{x}{{x}^{2}+1}$

Solución:

Iniciamos aplicando la propiedad del logaritmo de una potencia para simplificar la derivación.

$\mathrm{ln}\sqrt{{x}^{2}+1}=\mathrm{ln}{\left({x}^{2}+1\right)}^{\frac{1}{2}}=\frac{1}{2}\mathrm{ln}\left({x}^{2}+1\right)$

Aplicamos la derivada del logaritmo natural.

${f}^{\text{'}}\left(x\right)=\frac{1}{2}\cdot \frac{{\left({x}^{2}+1\right)}^{\text{'}}}{{x}^{2}+1}=\frac{1}{2}\cdot \frac{2x}{{x}^{2}+1}=\frac{x}{{x}^{2}+1}$

Finalmente:

${f}^{\text{'}}\left(x\right)=\frac{x}{{x}^{2}+1}$

Indicamos como respuesta correcta al inciso D.

Reactivo 67

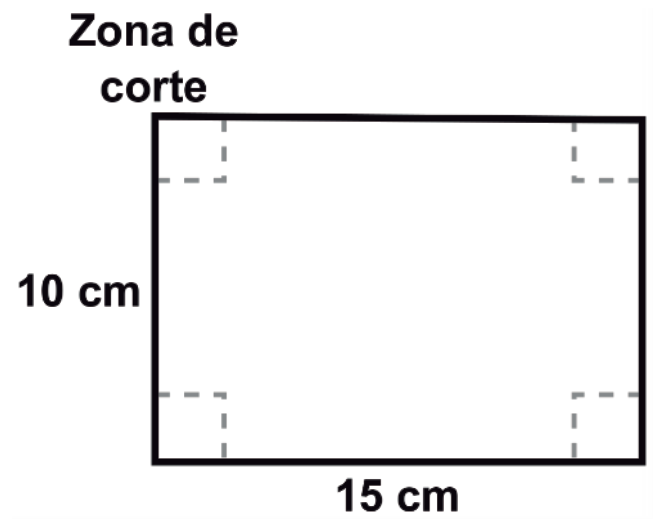
Se desea fabricar una caja sin tapa con una lámina de aluminio de 10 cm x 15 cm. ¿Cuánto se deberá cortar en cada esquina de la lámina para obtener el volumen máximo?

1. $\frac{25+5\sqrt{7}}{6}$
2. $\frac{25+5\sqrt{43}}{6}$
3. $\frac{25-5\sqrt{43}}{6}$
4. $\frac{25-5\sqrt{7}}{6}$

Solución:

Se trata de un problema de optimización, en el que debemos calcular la longitud a cortar en los cuadrados de las esquinas, para que el volumen de la caja sin tapa resultante sea máximo.

Iniciamos definiendo a dicha longitud desconocida como $x$ y que los cortes son cuadrados, aunque no se menciona en el problema.

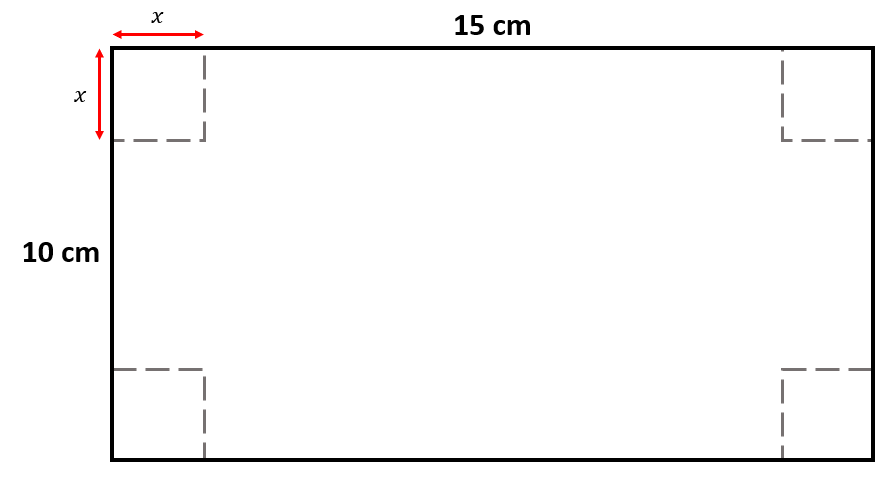
Ahora, debemos encontrar la ecuación que nos permitirá calcular el volumen de la caja una vez haya sido doblada. La altura de la caja será $x$, la profundidad $10-2x$ y la anchura $15-2x$.

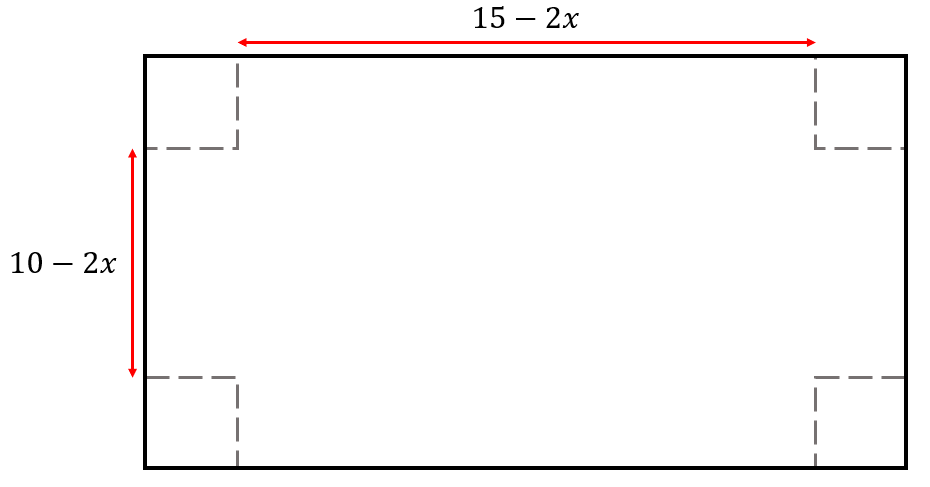
La expresión del volumen será:

$V=x\left(10-2x\right)\left(15-2x\right)$

Desarrollamos.

$V=4{x}^{3}-50{x}^{2}+150x$

Para encontrar el valor de $x$ que maximiza el volumen, debemos calcular la derivada de $V$ respecto de $x$ y luego igualar a cero.

${V}^{\text{'}}\left(x\right)=12{x}^{2}-100x+150$

Igualamos a cero.

$12{x}^{2}-100x+150=0\to 6{x}^{2}-50x+75=0$

Aplicando la fórmula de segundo grado nos queda:

${x}_{1}=\frac{25+5\sqrt{7}}{6},{x}_{2}=\frac{25-5\sqrt{7}}{6}$

Identificamos que valor de $x$ nos otorga el máximo evaluando en la función del volumen.

$V\left(\frac{25+5\sqrt{7}}{6}\right)=\frac{1250-875\sqrt{7}}{27}=-39.4456$

Descartamos este resultado. El valor de corte $x$ que permite obtener el máximo volumen es:

${x}_{MAX}=\frac{25-5\sqrt{7}}{6}\approx 1.9618$

$v\left({x}_{2}\right)=132.03\dots$

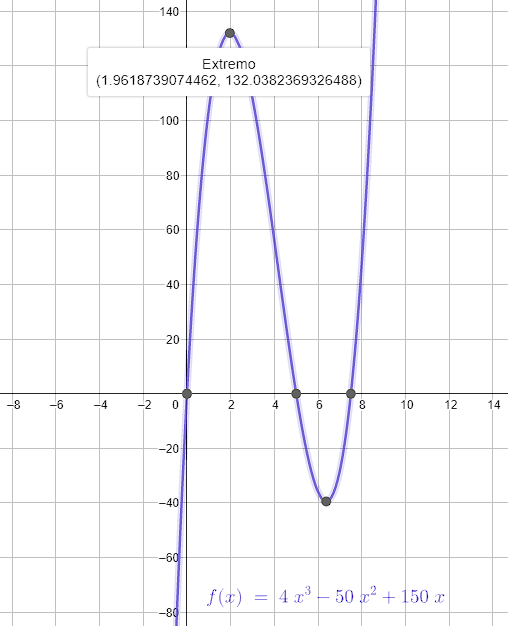
La respuesta correcta es el inciso D.

Reactivo 68

La $\int \sqrt{x}dx$ es igual a:

1. $\frac{1}{2\sqrt{x}}+C$
2. $\frac{3}{2}\sqrt{x}+C$
3. $\frac{2}{3}\sqrt{x}+C$
4. $\frac{2}{3}x\sqrt{x}+C$

Solución:

Iniciamos expresando a la función del integrando como una potencia.

$\int \sqrt{x}dx=\int {x}^{1/2}dx$

Ahora, aplicamos la fórmula de la integral para una potencia.

$\int {x}^{\frac{1}{2}}dx=\frac{{x}^{\frac{1}{2}+1}}{\frac{1}{2}+1}+C=\frac{{x}^{\frac{3}{2}}}{\frac{3}{2}}+C$

Reacomodamos:

$\frac{2}{3}{x}^{\frac{3}{2}}+C=\frac{2}{3}{x}^{\frac{1}{2}}\cdot x+C=\frac{2}{3}x\sqrt{x}+C$

Finalmente:

$\int \sqrt{x}dx=\frac{2}{3}x\sqrt{x}+C$

Indicamos como respuesta correcta al inciso D.

Reactivo 69

La $\int {\left(2x-1\right)}^{3}dx$ es igual a:

1. $\frac{{\left(2x-1\right)}^{2}}{6}+C$
2. $\frac{{\left(2x-1\right)}^{4}}{4}+C$
3. $\frac{{\left(2x-1\right)}^{2}}{2}+C$
4. $\frac{{\left(2x-1\right)}^{4}}{8}+C$

Solución:

Aplicamos un sencillo cambio de variable para resolver la integral.

$u=2x-1\to du=2dx\to dx=\frac{1}{2}du$

Implementando nos queda:

$\int {\left(2x-1\right)}^{3}dx\to \frac{1}{2}\int {u}^{3}du$

Integramos aplicando la fórmula de una potencia.

$\frac{1}{2}\int {u}^{3}du=\frac{1}{2}\frac{{u}^{3+1}}{3+1}+C=\frac{1}{2}\frac{{u}^{4}}{4}+C=\frac{{u}^{4}}{8}+C$

Devolvemos el cambio de variable.

$\frac{{u}^{4}}{8}+C\to \frac{{\left(2x-1\right)}^{4}}{8}+C$

Finalmente:

$\int {\left(2x-1\right)}^{3}dx=\frac{{\left(2x-1\right)}^{4}}{8}+C$

Concluimos indicando como respuesta correcta al inciso D.